修正

(2017/5/31) コメントの指摘を受け、行列積(ELM Step2)とタイポ(xとXの間違い)を修正しました。

元記事

論文を読んでいたらELM！ELM！と何回も見たのでGoogle検索するとデンソーITラボラトリの技術ブログがヒットしました。

Denso IT Laboratory 技術ブログ Extreme Learning Machine

実装が簡単と書いてあったので、書いて動作を確認してみました。Juliaは0.4.6、グラフはPyPlot、他には何も使ってないと思います。

using PyPlot

# 訓練データ
x = -10:0.1:10
N = length(x)
y = sinc(x)
X = [ones(N) x]
M = 2

# 活性化関数
sigmoid(x) = 1 ./ (1 .+ exp(-x))

# 隠れノード数
L = 64

# グラフを描く (訓練データ)
plot(x, y, "r--")
savefig("correct.png")

# ELM STEP1: ランダムに作成
a = rand(L, M)
b = rand(L)

# ELM STEP2: 隠れ層の出力行列Hを生成
H = zeros(N, L)
# for i=1:N, l=1:L
#    H[i, l] = sigmoid( a[l, :]'*x[i,:] + b[l] )[1]
# end
H = sigmoid.(X * a' .+ b')

# ELM STEP3: T=Hβの解を求める
β = pinv(H) * y

# 予測する
y_pred = zeros(N)
for i=1:N
    for l=1:L
        # y_pred[i] += β[l] * sigmoid( a[l, :]' * x[i, :] + b[l] )[1]
        y_pred[i] += β[l] * sigmoid( a[l, :]' * X[i, :] + b[l] )[1]
    end
end

# 予測と正解を重ねて描く
plot(x, y, "r--")
plot(x, y_pred, "b--")
savefig("compare_L=$L.png")

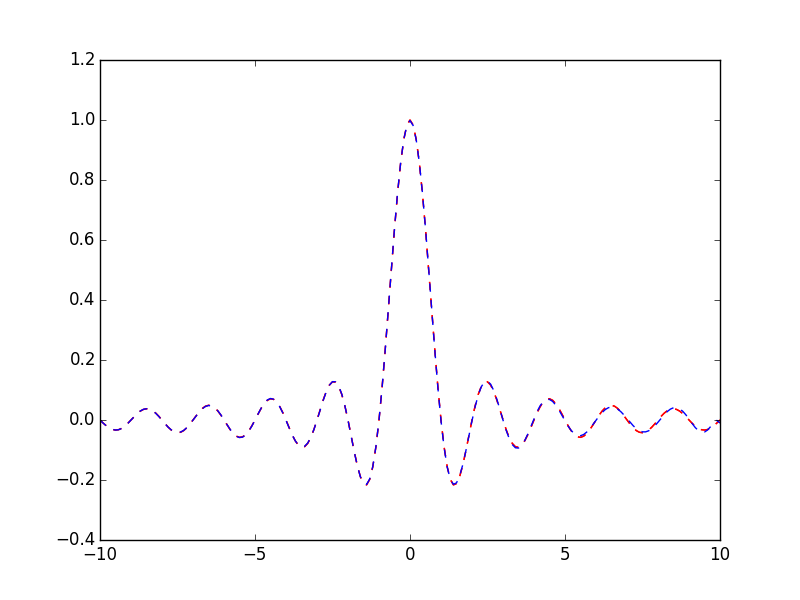
隠れ層のノード数Lを64で試すと次のようになりました。だいたい一致してますね（特にコメントがない）。

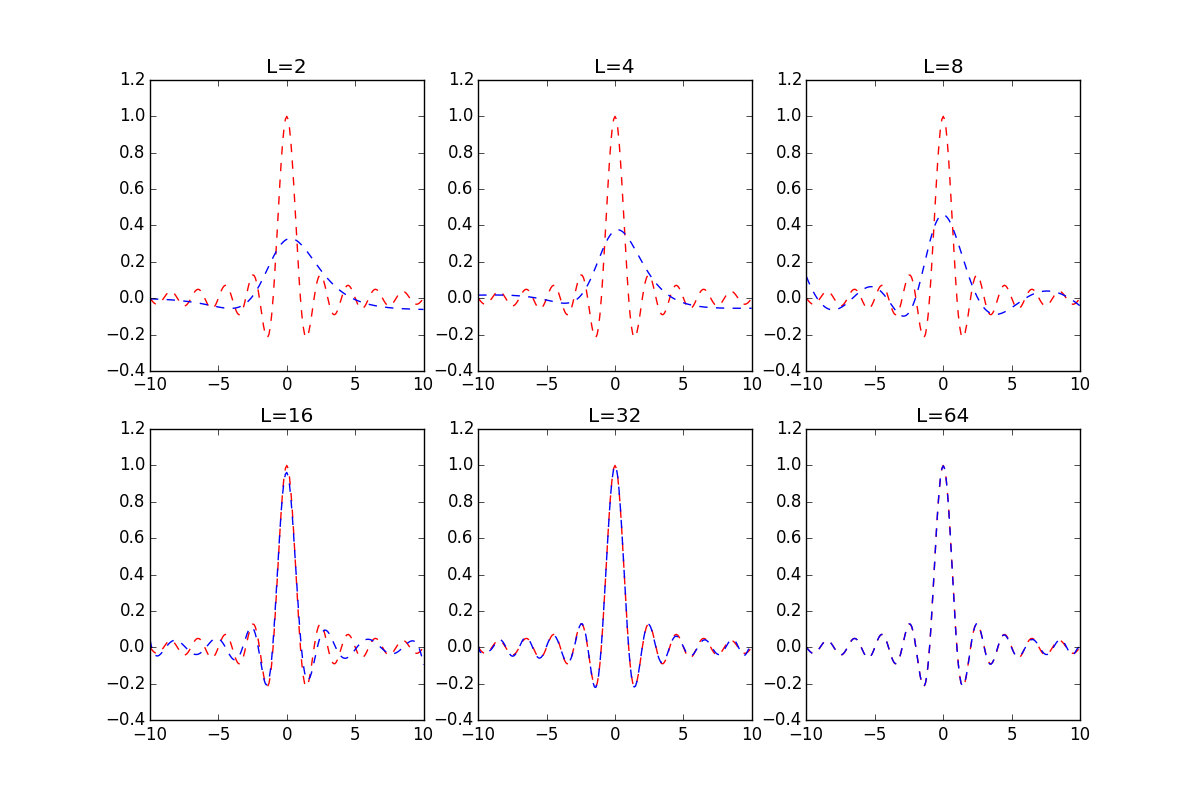
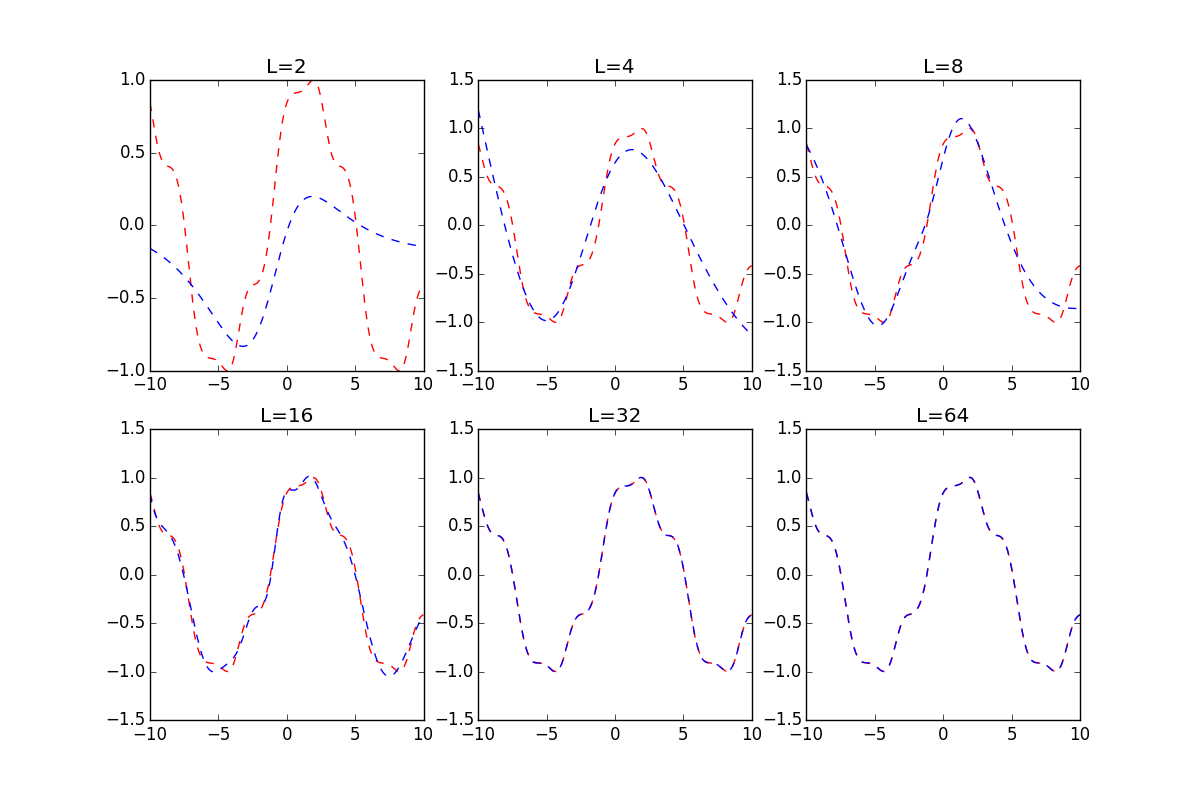
Lの数を変えて試したものを2つ載せておきます。
1. $\mathrm{sinc}(x)$
2. $\sin(0.5x + \cos(\sin(x))$

JuliaでExtreme Learning Machineを書く

修正

元記事