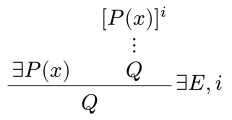Leanで紐解く論理パズル

はじめに

本記事は理情 Advent Calendar 2025¹の5日目の記事²³です。

この記事では、Leanを用いて⁴自身の作成した論理パズル及びその解答の正しさを検証します。

もしよければ他の方の記事も是非ご覧ください。

前提

この記事では関数型言語に関する基本的な知識(ラムダ抽象、パターンマッチ、ヴァリアントなど)および一階述語論理や自然演繹に関する知識を前提としています。

Leanについての知識がなくてもこれらの知識があれば理解はできると思いますが、Leanについての詳細な説明は省いているため、必要な情報は適宜補ってください。

筆者はLeanに関してほぼ素人です。
明らかな誤りなどが含まれている可能性がありますので、何かお気づきの点があればコメントで指摘していただけますと幸いです。

Leanとは

関数型言語かつ定理証明支援系の言語です。普通の関数型言語としても使えますし、Coqのように定理証明にも使えます。

mathlib4というライブラリがあり、大学数学もある程度記述できるようです⁵。

公式HPはこちら。

Curry-Howard同型

簡単に言うと論理式と型付きラムダ計算に対応があるというものです。

Leanではtacticと呼ばれるものを用いて証明を行うこともできますが、今回は折角関数型言語を使っている(&もうすぐ授業でこれを取り扱う)ので、このCurry-Howard同型に忠実に従いつつ、なるべく自然演繹に近い形で証明を進めていこうと思います。

※この項は後日加筆します。気になる方はWikipediaなどをご参照ください。

対象となる論理パズル

私は今年に入ってから東方Project⁶の二次創作小説を執筆するようになったのですが⁷、最初に執筆した作品でなんとなく論理パズルを入れることにしました。

ここでいう論理パズルとは「文章で説明される各種条件に対して論理的に矛盾しない解を見つけるパズル」とします。たとえ常識に反しているような解であっても、(古典)論理に基づいて⁸各種前提に矛盾していないものであれば解として認められます。また、解は複数存在しても良く、その一つを求められれば十分であるとします。極端な話、互いに矛盾する条件が課されている場合は、爆発律よりいかなる命題も導けるので、適当な命題を一つ答えればパズルが解けたことになります。

場面設定

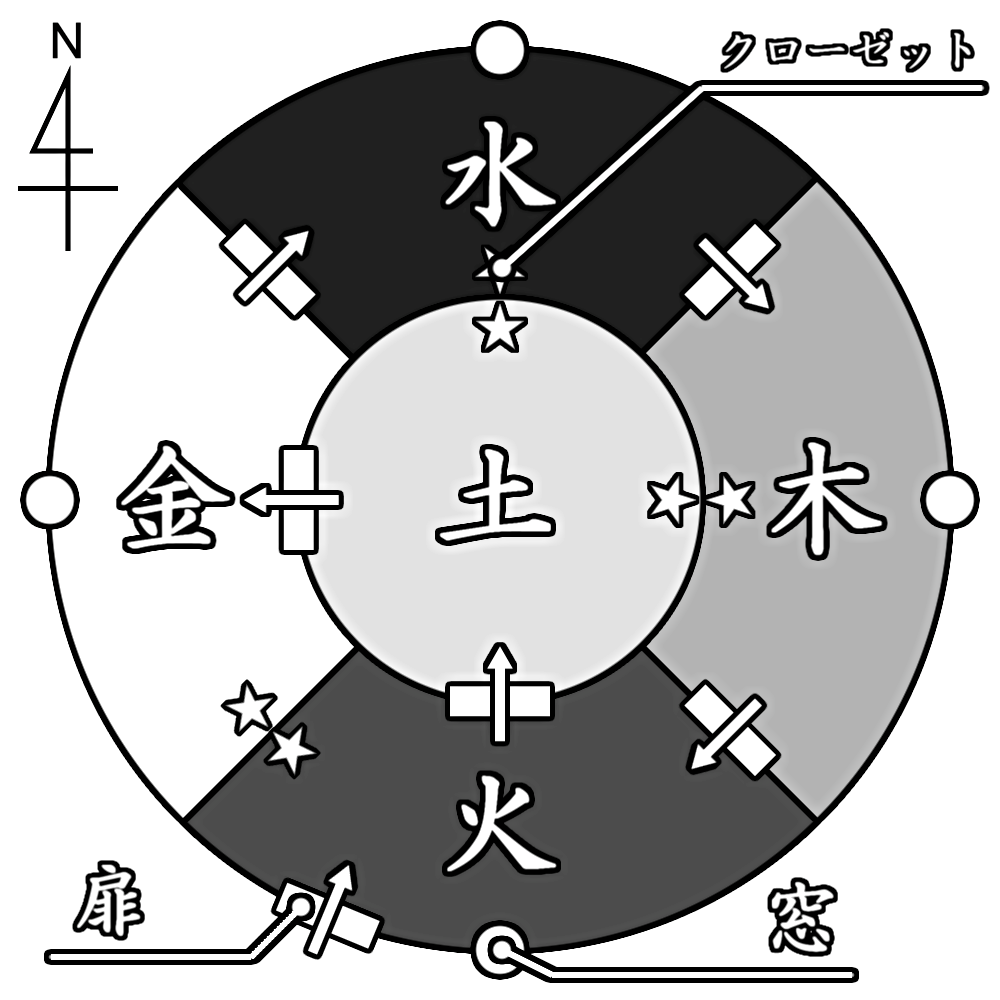
火・土・金・水・木の五つの部屋がある建物があります。それぞれの部屋には一方通行の扉があり、逆戻りはできません(扉を開けっ放しにすれば戻れますがそれはできないことにします)。また、各部屋には窓とクローゼットがありますが、窓を介して部屋の外に移動することはできません。

主人公らは一方通行の扉を介して火の間に入り、そこでゲームスタートです。ここからこの建物にある部屋を介して建物の外に脱出できるので、それを探すのがこのゲームの目標です。

以下の図は、主人公らが五つの部屋を巡った結果を元に作成した図で、図中の矢印は扉を介して移動できる方向を示しています。なお、この図はAviUtl⁹で作成しています。

この図を見ると分かる通り、一見すると火→土→金→水→木→火→……という向きにしか移動できず、同じ場所を回り続けることになりそうです。しかしながら、各部屋には脱出のためのヒントが置かれており、これを組み合わせることで脱出ができそうです。

脱出のヒント(本題)

ここからが論理パズルの本題です。

各部屋からは次のような条件が得られました。

1. 火は土金木のいずれかのみを生む
2. 土はあるものによってのみ生まれ、金のみを生む
3. 金は火から生まれるあるものによってのみ生まれ、火を生まない
4. 水は火土金のいずれかによってのみ生まれ、木のみを生む
5. 木はあるものによってのみ生まれ、火のみを生む

また、大前提として

• 各要素は必ずあるものを生み、あるものによって生まれるが、自分自身を生むことはない

というのがあるようです。

シンプルに考えると……

先程の部屋の配置図を見ると、火→土→金→水→木→火→……という向きに移動ができます。ヒントとの関係性を考えると、なんとなく「火が土を生み、土が金を生み、金が水を生み、水が木を生み、木が火を生む」という関係が成り立っているような気がします。

実を言うと、この関係は五行説における「相生」にほかなりません。火が燃えると残った灰は土に還り、土を掘ることで金属を得ることができ、金属の表面には水が生じ、水によって木が成長し、木が燃えることで火を生む。

実際に先程の1-5の関係にこれを当てはめてみると、この解は1-5の条件を満たします(自然言語での説明は今回は省くので各自考えてみてください)。つまり、「部屋Aから部屋Bに移動できる」というのは「AがBを生む」という関係に対応していそうです。

ということは、この建物から脱出するには「火が土を生み、土が金を生み、金が水を生み、水が木を生み、木が火を生む」という自明な関係(以下では「相生関係」と書きます)以外に何らかの関係が成り立っていなければなりません。そのような関係(のうち1つ)を見つけるのがこの論理パズルの目標となります。

Leanによる検証

一階述語論理への翻訳

問題設定を把握したところで、早速Leanによって「火が土を生み、土が金を生み、金が水を生み、水が木を生み、木が火を生む」という関係が成り立つことを示しましょう。

Leanによる検証をするために、まず今回の問題設定を一階述語論理に落とし込む必要があります。

述語P(x, y)を「xがyを生む」と定義します。このとき、同時に「yがxによって生まれる」というのも成り立つこととします。

先程の5つの条件を眺めてみると、「AはBによってのみ生まれる」「AはBのみを生む」といった表現があることがわかるので、これらが略記できると便利です。

「Q(x)であるようなxがただ一つ存在する」というのは$\exists x.(Q(x) \land (\forall y. (Q(y) \rightarrow Q(x)))$とかけるので、これらはLeanで以下のように記述できます。

なお、Leanにおいて$P(x, y)$は関数$P$に$x$と$y$を適用させたもの$P\ x \ y$として扱われます。また、elementは要素の型です。

-- xはyのみによって生まれる
def only_by (P : element → element → Prop) (x y : element) : Prop :=
  P y x ∧ ∀ z, P z x → z = y

-- xはyのみを生む
def only_to (P : element → element → Prop) (x y : element) : Prop :=
  P x y ∧ ∀ z, P x z → z = y

これらと述語Pを用いると、先程の1-5の条件(ここではh1-h5と命名しました)と大前提(ここではproduceと命名しました)は次のように書けます。なお、(明記していませんでしたが)5つの要素は相異なっていてほしいので、それに対応する規則distinctも設けてあります。

$a \neq b$は$a = b \rightarrow False$の略記です。

structure FiveElementsBase (element : Type) where
  fire: element
  earth: element
  metal: element
  water: element
  wood: element
  P : element → element → Prop

  -- 火は土か金か木のいずれかのみを生む
  h1 : ∃ x : element, (x = earth ∨ x = metal ∨ x = wood) ∧ (only_to P fire x)

  -- 土はあるものによってのみ生まれ、金のみを生む
  h2 : (∃ x : element, only_by P earth x) ∧ (only_to P earth metal)

  -- 金は火から生まれるあるものによってのみ生まれ、火を生まない
  h3 : (∃ x : element, P fire x ∧ only_by P metal x) ∧ ¬ P metal fire

  -- 水は火土金のいずれかによってのみ生まれ、木のみを生む
  h4 : (∃ x : element, (x = fire ∨ x = earth ∨ x = metal) ∧ only_by P water x) ∧ (only_to P water wood)

  -- 木はあるものによってのみ生まれ、火のみを生む
  h5 : (∃ x : element, only_by P wood x) ∧ (only_to P wood fire)

  -- 各要素は必ず何かを生み、何かによって生まれ、自己生産しない
  produce : ∀ x : element, (∃ y : element, P y x) ∧ (∃ z : element, P x z) ∧ ¬ P x x

  -- 各要素は相異なる
  distinct : (fire ≠ earth) ∧ (fire ≠ metal) ∧ (fire ≠ water) ∧ (fire ≠ wood) ∧
             (earth ≠ metal) ∧ (earth ≠ water) ∧ (earth ≠ wood) ∧
             (metal ≠ water) ∧ (metal ≠ wood) ∧
             (water ≠ wood)

相生関係が成り立つことの証明

本記事で一番重厚な部分です。ひたすら証明をしていくだけなので退屈かとは思いますが、興味があれば是非お読みください。

取り敢えず後のことを考え、この証明はsectionによって区切ることにし、以下のように略記をすることにします。

variable {element : Type}
variable {f : FiveElementsBase element}

local notation "fire" => f.fire
local notation "earth" => f.earth
local notation "metal" => f.metal
local notation "water" => f.water
local notation "wood" => f.wood
local notation "P" => f.P
local notation "distinct" => f.distinct
local notation "produce" => f.produce
local notation "h1" => f.h1
local notation "h2" => f.h2
local notation "h3" => f.h3
local notation "h4" => f.h4
local notation "h5" => f.h5

それでは、順に相生関係を見ていきましょう。なお、わかりやすさのため、使用している条件などをその都度冒頭に記しています。

水は木のみを生む

まずは簡単な水・木から。この命題はh4にそのままありますね。以下の連言除去規則を用いることで証明終了です。

$$ \frac{A \land B}{B} \land E $$

Leanにおいて、連言はleftとrightの2つのフィールドと、唯一のコンストラクタintroからなる帰納型として扱われます(単なる組と考えても差し支えありません)。ここで、$A \land B$は無名コンストラクタ⟨ha, hb⟩(ただしha: A, hb: B)と略記できます。今回は連言の右側にアクセスしたいので.rightを使います。

ちなみに、一つ後の証明で見ますが、$\land$の導入規則はこの無名コンストラクタを使って表記することと同じです。

$$ \frac{A \quad B}{A \land B} \land I $$

なお、notationを利用している関係で(h4)というように()でくくる必要があります。

h4 : (∃ x : element, (x = fire ∨ x = earth ∨ x = metal) ∧ only_by P water x) ∧ (only_to P water wood)

theorem water_produces_only_wood : only_to P water wood :=
  (h4).right

木は水のみによって生まれる

h4の右側には「水は木のみを生む」、h5の左側には「木はあるものによってのみ生まれる」と記述されています。なので、この「あるもの」が「水」である、ということをいえば良いです。h5の左側にはonly_byがあるので、以下の存在量化子の除去規則を使うことになります¹⁰。なお、$Q$および$P(x)$以外の開いた前提において$x$は自由変項として現れない、という固有変数条件が課されます。

$\exists x : \alpha.P(x)$は無名コンストラクタh = ⟨w, hpw⟩(ただしw: α, hpw: P x)を用いて表記でき、パターンマッチによってこれらを抽出することができます。let ⟨w, hpw⟩ = hはその略記であり、これらからwとは無関係な命題qを証明できれば、存在量化子を除去できたことになります。以下の例ではhx.rightは∀ z, P z wood → z = xです。なお、導入規則は$\land$と同様に無名コンストラクタによる表記が可能です。

含意$P \rightarrow Q$はfun hp => hq(ただしhp: P, hq: Q)というラムダ抽象によって表現されます。導入規則は単にこれに沿って書き換えるだけです。全称量化子$\forall x : \alpha.P(x)$も含意と同様にラムダ抽象fun x => hpx(ただしx: α, hpx: P x)で表されます。いずれの場合も除去規則は関数適用であり、例えばhx.rightにwaterとP water woodを順に与えるとwater = xが導けます。

等号$a=b$については馴染みがない方もいるかも知れませんが、これについても導入規則・除去規則があります。左側は反射律(LeanではEq.refl)、右側は代入(LeanではEq.rec)で、これらから対称律と推移律も導けます。Leanにおける▸は必要に応じて対称律を適用してから代入を行うものです。以下の例ではwater = xをy = xに代入する際に対称律を用いる必要があります。

$$ \frac{}{a = a} = I \qquad \frac{a = b \hspace{5mm} P(a)}{P(b)} = E $$

なお、以下の証明ではhaveを用いることで何を示したいかを明確にしています。本質的にはletと同じですが、個人的には簡単な補題を示すときはhaveを、単なるラベル付けのときはletを使う、という使い分けをしています。

def only_by (P : element → element → Prop) (x y : element) : Prop :=
  P y x ∧ ∀ z, P z x → z = y

h4 : (∃ x : element, (x = fire ∨ x = earth ∨ x = metal) ∧ only_by P water x) ∧ (only_to P water wood)
h5 : (∃ x : element, only_by P wood x) ∧ (only_to P wood fire)

theorem only_water_produces_wood : only_by P wood water :=
  let water_to := And.right (h4)
  let wood_by := And.left (h5)
  let ⟨x, hx⟩ := wood_by
  have water_eq_x : water = x := hx.right water (water_to.left)
  ⟨And.left water_to,
    fun y py =>
      have y_eq_x : y = x := hx.right y py
      water_eq_x ▸ y_eq_x⟩

木は火のみを生む

h5の右側にいるのでそれで終わりです。

h5 : (∃ x : element, only_by P wood x) ∧ (only_to P wood fire)

theorem wood_produces_only_fire : only_to P wood fire :=
  (h5).right

火は土のみを生む

一番大変な証明です。大まかな流れとしては、

• 木は水のみによって生まれる→火は木を生まない
• 金は火が生むあるものによってのみ生まれ、火は火を生まない→火は金を生まない
• 火は土金木のいずれかのみを生み、火は木も金も生まない→火は土のみを生む

という感じで単純ではあるのですが、いかんせん証明することが多いため証明が長くなってしまいます。

e |>.xは(e).xの略記で、特に複数回登場する()を減らすことができます。

否定$\lnot P$は$P \rightarrow False$と同じです。従って、否定の導入規則はこれをラムダ抽象で書くことに一致します。一方、否定の除去規則は$P \rightarrow False$に対応する型に$P$に対応する型を適用させるのと同じになります。また、爆発律($\bot E$)はFalse.elimに$False$を渡すことで適用できます。Leanではabsurd hp hnp(ただしhp: P, hnp: fun hp: P => False)とかくことでこれらを一気に適用してq: Qを得ることができます(これを使うと()が1つ減ります)。

$$\frac{P \quad \lnot P}{\bot} \lnot E \qquad \frac{\bot}{Q} \bot E$$

選言$P \lor Q$の導入規則はhp: P, hq: QのときOr.inl hpまたはOr.inr hqによって実現できます。選言はコンストラクタinlとinrを持つヴァリアント(Rustでいえばenum)のようなものだと思ってください。

$$\frac{P}{P \lor Q} \lor I \quad \frac{Q}{P \lor Q} \lor I$$

選言の除去規則はパターンマッチによって取り出すことと等しいです。Or.inl hで左側の命題を、Or.inr hで右側の命題をhに格納し、両方から同じ命題を導くことができれば除去ができます。$P \lor (Q \lor R)$のようにネストされた選言については、パターンマッチをネストすることなく、Or.inr (Or.inl h)というように条件がかけます。なお、Leanにおいて$\land$や$\lor$は右結合です。

def only_by (P : element → element → Prop) (x y : element) : Prop :=
  P y x ∧ ∀ z, P z x → z = y

h1 : ∃ x : element, (x = earth ∨ x = metal ∨ x = wood) ∧ (only_to P fire x)
h3 : (∃ x : element, P fire x ∧ only_by P metal x) ∧ ¬ P metal fire
produce : ∀ x : element, (∃ y : element, P y x) ∧ (∃ z : element, P x z) ∧ ¬ P x x
distinct : (fire ≠ earth) ∧ (fire ≠ metal) ∧ (fire ≠ water) ∧ (fire ≠ wood) ∧
           (earth ≠ metal) ∧ (earth ≠ water) ∧ (earth ≠ wood) ∧
           (metal ≠ water) ∧ (metal ≠ wood) ∧
           (water ≠ wood)
only_water_produces_wood : only_by P wood water

theorem fire_produces_only_earth : only_to P fire earth :=
  let wood_only_by_water := only_water_produces_wood -- 木は水のみによって生まれる
  let fire_neq_water := distinct |>.right.right.left -- 火と水は異なる
  have fire_doesnt_produce_wood : ¬ P fire wood := -- 火は木を生まない
    fun fire_produces_wood : P fire wood =>
      let fire_eq_water := wood_only_by_water.right fire fire_produces_wood
      fire_neq_water fire_eq_water
  have fire_doesnt_produce_metal : ¬ P fire metal := -- 火は金を生まない
    fun fire_produces_metal : P fire metal =>
      let metal_by := (h3).left
      let ⟨_, hx⟩ := metal_by
      let fire_eq_x := hx.right.right fire fire_produces_metal
      let fire_produces_fire := fire_eq_x ▸ hx.left
      have fire_doesnt_produce_fire := (produce fire) |>.right.right -- 火は火を生まない
      fire_doesnt_produce_fire fire_produces_fire
  have fire_only_to_earth : only_to P fire earth :=
    let ⟨y, hy⟩ := h1
    let fire_produces_y := hy.right.left
    have y_eq_earth : y = earth := -- yは土である
      have y_neq_metal : y ≠ metal :=
        fun y_eq_metal : y = metal =>
          fire_doesnt_produce_metal (y_eq_metal ▸ fire_produces_y)
      have y_neq_wood : y ≠ wood :=
        fun y_eq_wood : y = wood =>
          fire_doesnt_produce_wood (y_eq_wood ▸ fire_produces_y)
      match hy.left with
      | Or.inl h => h
      | Or.inr (Or.inl h) => absurd h y_neq_metal
      | Or.inr (Or.inr h) => absurd h y_neq_wood
    y_eq_earth ▸ hy.right
  fire_only_to_earth

金は土のみによって生まれる

ここまでで一通り説明をしたので、ここからしばらくは証明の方針を軽く述べて終わりにします。

金は火から生まれるあるものによってのみ生まれるので、火が土を生むことと合わせるとこれが示せます。

def only_to (P : element → element → Prop) (x y : element) : Prop :=
  P x y ∧ ∀ z, P x z → z = y

h3 : (∃ x : element, P fire x ∧ only_by P metal x) ∧ ¬ P metal fire
fire_produces_only_earth : only_to P fire earth

theorem only_earth_produces_metal : only_by P metal earth :=
  let earth_by := (h3).left
  let ⟨x, hx⟩ := earth_by
  have x_eq_earth : x = earth :=
    let fire_only_to_earth := fire_produces_only_earth
    let fire_produces_x := hx.left
    fire_only_to_earth.right x fire_produces_x
  x_eq_earth ▸ hx.right

土は火のみによって生まれる

土はあるものによってのみ生まれるので、火が土を生むことと合わせるとこれが示せます。

def only_by (P : element → element → Prop) (x y : element) : Prop :=
  P y x ∧ ∀ z, P z x → z = y
def only_to (P : element → element → Prop) (x y : element) : Prop :=
  P x y ∧ ∀ z, P x z → z = y

h2 : (∃ x : element, only_by P earth x) ∧ (only_to P earth metal)
fire_produces_only_earth : only_to P fire earth

theorem only_fire_produces_earth : only_by P earth fire :=
  let earth_by := (h2).left
  let ⟨x, hx⟩ := earth_by
  have fire_eq_x : fire = x :=
    let fire_only_to_earth := fire_produces_only_earth
    let fire_produces_earth := fire_only_to_earth.left
    hx.right fire fire_produces_earth
  fire_eq_x ▸ hx

土は金のみを生む

h2の右側にいるのでそれで終わりです。

h2 : (∃ x : element, only_by P earth x) ∧ (only_to P earth metal)

theorem earth_produces_only_metal : only_to P earth metal :=
  (h2).right

水は金のみによって生まれる

火が土を生むことの証明と同じです。

• 火は土のみを生む→火は水を生まない
• 土は金のみを生む→土は水を生まない
• 水は火土金のいずれかのみによって生まれるが、土も火も水を生まない→水は金のみによって生まれる

Eq.symmは対称律です。hoge.symmでhogeの左右を逆にしたものを得ることができます。

def only_to (P : element → element → Prop) (x y : element) : Prop :=
  P x y ∧ ∀ z, P x z → z = y

h4 : (∃ x : element, (x = fire ∨ x = earth ∨ x = metal) ∧ only_by P water x) ∧ (only_to P water wood)
distinct : (fire ≠ earth) ∧ (fire ≠ metal) ∧ (fire ≠ water) ∧ (fire ≠ wood) ∧
           (earth ≠ metal) ∧ (earth ≠ water) ∧ (earth ≠ wood) ∧
           (metal ≠ water) ∧ (metal ≠ wood) ∧
           (water ≠ wood)
fire_produces_only_earth : only_to P fire earth
earth_produces_only_metal : only_to P earth metal

theorem only_metal_produces_water : only_by P water metal :=
  let water_by := (h4).left
  let ⟨x, hx⟩ := water_by
  let x_produces_water := hx.right.left
  have x_eq_metal : x = metal :=
    have fire_neq_x : fire ≠ x :=
      fun fire_eq_x : fire = x =>
        let fire_only_to_earth := fire_produces_only_earth
        let fire_produces_water := fire_eq_x ▸ x_produces_water
        let water_eq_earth := fire_only_to_earth.right water fire_produces_water
        let earth_neq_water := distinct |>.right.right.right.right.right.left
        earth_neq_water water_eq_earth.symm
    have earth_neq_x : earth ≠ x :=
      fun earth_eq_x : earth = x =>
        let earth_only_to_metal := earth_produces_only_metal
        let earth_produces_water := earth_eq_x ▸ x_produces_water
        let water_eq_metal := earth_only_to_metal.right water earth_produces_water
        let metal_neq_water := distinct |>.right.right.right.right.right.right.right.left
        metal_neq_water water_eq_metal.symm
    match hx.left with
    | Or.inl h => absurd h fire_neq_x.symm
    | Or.inr (Or.inl h) => absurd h earth_neq_x.symm
    | Or.inr (Or.inr h) => h
  x_eq_metal ▸ hx.right

金は水を生む

水は金のみによって生まれるので、当然そこからこれが導けます。

def only_by (P : element → element → Prop) (x y : element) : Prop :=
  P y x ∧ ∀ z, P z x → z = y

only_metal_produces_water : only_by P water metal

theorem metal_produces_water : P metal water :=
  And.left only_metal_produces_water

木は火を生む

h5より木は火のみを生むので、木は火を生みます。

def only_to (P : element → element → Prop) (x y : element) : Prop :=
  P x y ∧ ∀ z, P x z → z = y

h5 : (∃ x : element, only_by P wood x) ∧ (only_to P wood fire)

theorem wood_produces_fire : P wood fire :=
  h5 |>.right.left

相生関係の証明

ここまで長々とやってきましたが、これで少なくとも相生関係が成り立つということが言えました。

theorem weak_five_relations :
  P fire earth ∧ P earth metal ∧ P metal water ∧ P water wood ∧ P wood fire :=
  ⟨fire_produces_only_earth |>.left,
  earth_produces_only_metal |>.left,
  metal_produces_water,
  water_produces_only_wood |>.left,
  wood_produces_fire⟩

要素が5つのときに相生関係以外が成り立たないことの証明

ここまでで相生関係が成り立つことはわかりましたが、これが示せたところで脱出の鍵にはなりません。

しかし、ここまでの結果をよく眺めると、only_byとonly_toをつけずに証明していたものが2つありました。

metal_produces_water : P metal water
wood_produces_fire : P wood fire

一方、以下のことが成り立つことも示しました。

only_metal_produces_water : only_by P water metal
wood_produces_only_fire : only_to P wood fire

ということは、「金が水以外のものを生む」可能性と「火が木以外によって生まれる」可能性がまだ残されています。ここが脱出の鍵になりそうです。

ただ、金が火・土・木を生んだり、火が土・金・水によって生まれる可能性も考えられます。そこで、一旦要素が5つしかないと仮定して、どのようなことが起こるか見ていきましょう(もうおわかりかと思いますが、「要素が5つしかない」というのは論理パズルの条件に課されていませんので、これが答えを導く上での鍵になります)。

準備

ここではFiveElementsBase構造体をextendしてFiveElementsNormal構造体を定義し、そこに「要素が5つしかない」という公理を追加することにします。この公理は次のように書けます。

structure FiveElementsNormal (element : Type) extends FiveElementsBase element where
  -- 各要素は火土金水木のいずれかである
  complete : ∀ x : element, x = fire ∨ x = earth ∨ x = metal ∨ x = water ∨ x = wood

以下では新しくsectionを区切ってnotationを再度定義していますが、これについては割愛します。

金は水のみを生む

要素が5つしかないとき、金は水のみを生むことがわかります。これは、

• h3より金は火を生まない
• 土は火のみによって生まれるので、金は土を生まない
• produceより金は金を生まない
• 木は水のみによって生まれるので、金は木を生まない
• completeより属性は火土金水木に限られるので、金は水のみを生む
  というように示すことができます。5つの要素すべてについてパターンマッチをしていることからわかるように、completeがなければこれを示すことはできません。

※そろそろ飽きてきたので冒頭の使用している公理等の説明は省くことにします。必要であれば各自遡ってください。

theorem metal_produces_only_water : only_to P metal water :=
  let metal_produces_water := metal_produces_water
  have only_condition : ∀ z : element, P metal z → z = water :=
    fun x: element =>
      -- 金がxを生むとき、xは水である(xが水以外の場合はdistinctにより矛盾するためx=waterが導かれる)
      fun metal_produces_x : P metal x =>
        match (complete x) with
        | Or.inl h => -- x = fire
          let metal_doesnt_produce_fire := And.right (h3)
          let metal_produces_fire := h ▸ metal_produces_x
          absurd metal_produces_fire metal_doesnt_produce_fire
        | Or.inr (Or.inl h) => -- x = earth
          let earth_only_by_fire := only_fire_produces_earth
          let metal_eq_fire := earth_only_by_fire.right metal (h ▸ metal_produces_x)
          let metal_neq_fire := distinct |>.right.left
          absurd metal_eq_fire metal_neq_fire.symm
        | Or.inr (Or.inr (Or.inl h)) => -- x = metal
          let metal_doesnt_produce_metal := produce metal |>.right.right
          let metal_produces_metal := h ▸ metal_produces_x
          absurd metal_produces_metal metal_doesnt_produce_metal
        | Or.inr (Or.inr (Or.inr (Or.inl h))) => -- x = water
          h
        | Or.inr (Or.inr (Or.inr (Or.inr h))) => -- x = wood
          let wood_only_by_water := only_water_produces_wood
          let metal_eq_water := wood_only_by_water.right metal (h ▸ metal_produces_x)
          let metal_neq_water := distinct |>.right.right.right.right.right.right.right.left
          absurd metal_eq_water metal_neq_water
  ⟨metal_produces_water, only_condition⟩

火は木のみによって生まれる

同様です。

• 火は火を生まない
• 土は金のみを生むので、土は火を生まない
• 金は火を生まない
• 水は木のみを生むので、水は火を生まない
• completeより属性は火土金水木に限られるので、火は木のみによって生まれる

theorem only_wood_produces_fire : only_by P fire wood :=
  let fire_produces_wood := h5 |>.right.left
  have only_condition : ∀ z : element, P z fire → z = wood :=
    fun x : element =>
      -- xが火を生むとき、xは木である(xが木以外の場合はdistinctにより矛盾するためx=woodが導かれる)
      fun x_produces_fire : P x fire =>
        match (complete x) with
        | Or.inl h => -- x = fire
          let fire_doesnt_produce_fire := produce fire |>.right.right
          let fire_produces_fire := h ▸ x_produces_fire
          absurd fire_produces_fire fire_doesnt_produce_fire
        | Or.inr (Or.inl h) => -- x = earth
          let earth_only_to_metal := earth_produces_only_metal
          let fire_eq_metal := earth_only_to_metal.right fire (h ▸ x_produces_fire)
          let fire_neq_metal := distinct |>.right.left
          absurd fire_eq_metal fire_neq_metal
        | Or.inr (Or.inr (Or.inl h)) => -- x = metal
          let metal_doesnt_produce_fire := And.right (h3)
          let metal_produces_fire := h ▸ x_produces_fire
          absurd metal_produces_fire metal_doesnt_produce_fire
        | Or.inr (Or.inr (Or.inr (Or.inl h))) => -- x = water
          let water_only_to_wood := water_produces_only_wood
          let fire_eq_wood := water_only_to_wood.right fire (h ▸ x_produces_fire)
          let fire_neq_wood := distinct |>.right.right.right.left
          absurd fire_eq_wood fire_neq_wood
        | Or.inr (Or.inr (Or.inr (Or.inr h))) => -- x = wood
          h
  ⟨fire_produces_wood, only_condition⟩

相生関係以外が成り立たないことの証明

これも全要素についてパターンマッチです。何か他のものを生もうとするとonly_toに阻まれます。

theorem strong_five_relations :
  ∀ x y : element, P x y →
    (x = fire ∧ y = earth) ∨
    (x = earth ∧ y = metal) ∨
    (x = metal ∧ y = water) ∨
    (x = water ∧ y = wood) ∨
    (x = wood ∧ y = fire) :=
  fun x y px_y =>
    match (complete x) with
    | Or.inl h => -- x = fire
      let fire_only_to_earth := fire_produces_only_earth
      let y_eq_earth := fire_only_to_earth.right y (h ▸ px_y)
      Or.inl ⟨h, y_eq_earth⟩
    | Or.inr (Or.inl h) => -- x = earth
      let earth_only_to_metal := earth_produces_only_metal
      let y_eq_metal := earth_only_to_metal.right y (h ▸ px_y)
      Or.inr (Or.inl ⟨h, y_eq_metal⟩)
    | Or.inr (Or.inr (Or.inl h)) => -- x = metal
      let metal_only_to_water := metal_produces_only_water
      let y_eq_water := metal_only_to_water.right y (h ▸ px_y)
      Or.inr (Or.inr (Or.inl ⟨h, y_eq_water⟩))
    | Or.inr (Or.inr (Or.inr (Or.inl h))) => -- x = water
      let water_only_to_wood := water_produces_only_wood
      let y_eq_wood := water_only_to_wood.right y (h ▸ px_y)
      Or.inr (Or.inr (Or.inr (Or.inl ⟨h, y_eq_wood⟩)))
    | Or.inr (Or.inr (Or.inr (Or.inr h))) => -- x = wood
      let wood_only_to_fire := wood_produces_only_fire
      let y_eq_fire := wood_only_to_fire.right y (h ▸ px_y)
      Or.inr (Or.inr (Or.inr (Or.inr ⟨h, y_eq_fire⟩)))

ということで、要素が5つしかない場合はこの論理パズルに対する解はありません。

論理パズルの解答とその証明

※一応ネタバレに配慮して見出しはぼかしています。このセクション内の他の見出しについても同様です。

要素が5つでは解がないことがわかったので、要素が6つからなり、6つ目の要素がnewであると仮定してみましょう。

先で見た通り、「金が水以外のものを生む」可能性と「火が木以外によって生まれる」可能性がありました。ということは、「金がnewを生み、newが火を生む」という関係が成り立つ可能性があります。ただ、これが成り立つことは保証されるのでしょうか。

ここで条件をもう一度振り返ってみると、「各要素は必ずあるものを生み、あるものによって生まれるが、自分自身を生むことはない」というものがありました。ということは、要素が6つしか存在しないのであれば、それは火を生み、金によって生まれなければなりません。なぜなら、火以外がnewによって生まれることはなく、また金以外がnewを生むことはないからです。

準備

先程のcompleteと同様、要素が6つしかないという制約complete_6を設けます。また、6つ目の要素が他のどの要素とも異なるという制約distinct_newも設けます。

structure FiveElementsNew (element : Type) extends FiveElementsNormal element where
  new : element

  complete_6 : ∀ x : element, x = fire ∨ x = earth ∨ x = metal ∨ x = water ∨ x = wood ∨ x = new
  
  distinct_new : (new ≠ fire) ∧ (new ≠ earth) ∧ (new ≠ metal) ∧ (new ≠ water) ∧ (new ≠ wood)

証明1

newは金のみによって生まれることを示します。

方針としては先に述べたとおりです。produceによって「各要素は必ずあるものを生み、あるものによって生まれるが、自分自身を生むことはない」という制約が課されており、金以外のどの要素もonly_toの制約によりnewを生めないため、必然的に金のみがnewを生むことになります。

以下の証明ではまず∀ x : element, P x new → (x = metal ∧ P metal new)を示し、そこからP metal newと∀ x : element, P x new → x = metalを取り出して$\land$で結合しています。これによりパターンマッチを一回するだけで済みます。多分できるんだろうなぁと思って何も考えずにGPT-5.2に聞きました、賢いですね。

theorem only_metal_produces_new : only_by P new metal :=
  have fire_doesnt_produce_new : ¬ P fire new := -- 火はnewを生まない
    fun fire_produces_new : P fire new =>
      let new_eq_earth := fire_produces_only_earth.right new fire_produces_new
      let new_neq_earth := (distinct_new).right.left
      new_neq_earth new_eq_earth
  have earth_doesnt_produce_new : ¬ P earth new := -- 土はnewを生まない
    fun earth_produces_new : P earth new =>
      let new_eq_metal := earth_produces_only_metal.right new earth_produces_new
      let new_neq_metal := (distinct_new).right.right.left
      new_neq_metal new_eq_metal
  have water_doesnt_produce_new : ¬ P water new := -- 水はnewを生まない
    fun water_produces_new : P water new =>
      let new_eq_wood := water_produces_only_wood.right new water_produces_new
      let new_neq_wood := (distinct_new).right.right.right.right
      new_neq_wood new_eq_wood
  have wood_doesnt_produce_new : ¬ P wood new := -- 木はnewを生まない
    fun wood_produces_new : P wood new =>
      let new_eq_fire := wood_produces_only_fire.right new wood_produces_new
      let new_neq_fire := (distinct_new).left
      new_neq_fire new_eq_fire
  have new_doesnt_produce_new : ¬ P new new := produce new |>.right.right -- newはnewを生まない
  have analyze_produces_new : ∀ x : element, P x new → (x = metal ∧ P metal new) :=
    fun x x_produces_new =>
      match complete_6 x with
      | Or.inl h =>
          absurd (h ▸ x_produces_new) fire_doesnt_produce_new
      | Or.inr (Or.inl h) =>
          absurd (h ▸ x_produces_new) earth_doesnt_produce_new
      | Or.inr (Or.inr (Or.inl h)) =>
          ⟨h, h ▸ x_produces_new⟩
      | Or.inr (Or.inr (Or.inr (Or.inl h))) =>
          absurd (h ▸ x_produces_new) water_doesnt_produce_new
      | Or.inr (Or.inr (Or.inr (Or.inr (Or.inl h)))) =>
          absurd (h ▸ x_produces_new) wood_doesnt_produce_new
      | Or.inr (Or.inr (Or.inr (Or.inr (Or.inr h)))) =>
          absurd (h ▸ x_produces_new) new_doesnt_produce_new
  have metal_produces_new : P metal new :=
    have some_produces_new : ∃ x : element, P x new := (produce new).left
    let ⟨x, x_produces_new⟩ := some_produces_new
    analyze_produces_new x x_produces_new |>.right
  have only_condition : ∀ z : element, P z new → z = metal :=
    fun z z_produces_new =>
      analyze_produces_new z z_produces_new |>.left
  ⟨metal_produces_new, only_condition⟩

証明2

newは火のみを生むことを示します。方針は同じなので割愛します。

theorem new_produces_only_fire : only_to P new fire :=
  have new_doesnt_produce_earth : ¬ P new earth := -- newは土を生まない
    fun new_produces_earth : P new earth =>
      let new_eq_fire := only_fire_produces_earth.right new new_produces_earth
      let new_neq_fire := (distinct_new).left
      new_neq_fire new_eq_fire
  have new_doesnt_produce_metal : ¬ P new metal := -- newは金を生まない
    fun new_produces_metal : P new metal =>
      let new_eq_earth := only_earth_produces_metal.right new new_produces_metal
      let new_neq_earth := (distinct_new).right.left
      new_neq_earth new_eq_earth
  have new_doesnt_produce_water : ¬ P new water := -- newは水を生まない
    fun new_produces_water : P new water =>
      let new_eq_metal := only_metal_produces_water.right new new_produces_water
      let new_neq_metal := (distinct_new).right.right.left
      new_neq_metal new_eq_metal
  have new_doesnt_produce_wood : ¬ P new wood := -- newは木を生まない
    fun new_produces_wood : P new wood =>
      let new_eq_water := only_water_produces_wood.right new new_produces_wood
      let new_neq_water := (distinct_new).right.right.right.left
      new_neq_water new_eq_water
  have new_doesnt_produce_new : ¬ P new new := produce new |>.right.right -- newはnewを生まない
  have analyze_new_produces : ∀ x : element, P new x → x = fire ∧ P new fire :=
    fun x new_produces_x =>
      match complete_6 x with
      | Or.inl h =>
          ⟨h, h ▸ new_produces_x⟩
      | Or.inr (Or.inl h) =>
          absurd (h ▸ new_produces_x) new_doesnt_produce_earth
      | Or.inr (Or.inr (Or.inl h)) =>
          absurd (h ▸ new_produces_x) new_doesnt_produce_metal
      | Or.inr (Or.inr (Or.inr (Or.inl h))) =>
          absurd (h ▸ new_produces_x) new_doesnt_produce_water
      | Or.inr (Or.inr (Or.inr (Or.inr (Or.inl h)))) =>
          absurd (h ▸ new_produces_x) new_doesnt_produce_wood
      | Or.inr (Or.inr (Or.inr (Or.inr (Or.inr h)))) =>
          absurd (h ▸ new_produces_x) new_doesnt_produce_new
  have new_produces_fire : P new fire :=
    have some_produces_fire : ∃ x : element, P new x := produce new |>.right.left
    let ⟨x, new_produces_x⟩ := some_produces_fire
    analyze_new_produces x new_produces_x |>.right
  have only_condition : ∀ z : element, P new z → z = fire :=
    fun z new_produces_z =>
      analyze_new_produces z new_produces_z |>.left
  ⟨new_produces_fire, only_condition⟩

証明3

ここまでの結果から、火が土を生み、土が金を生み、金がnewを生み、newが火を生む、という関係が成り立ちます。

theorem anoter_relation :
  P fire earth ∧ P earth metal ∧ P metal new ∧ P new fire :=
  ⟨fire_produces_only_earth |>.left,
  earth_produces_only_metal |>.left,
  only_metal_produces_new |>.left,
  new_produces_only_fire |>.left⟩

ゴール

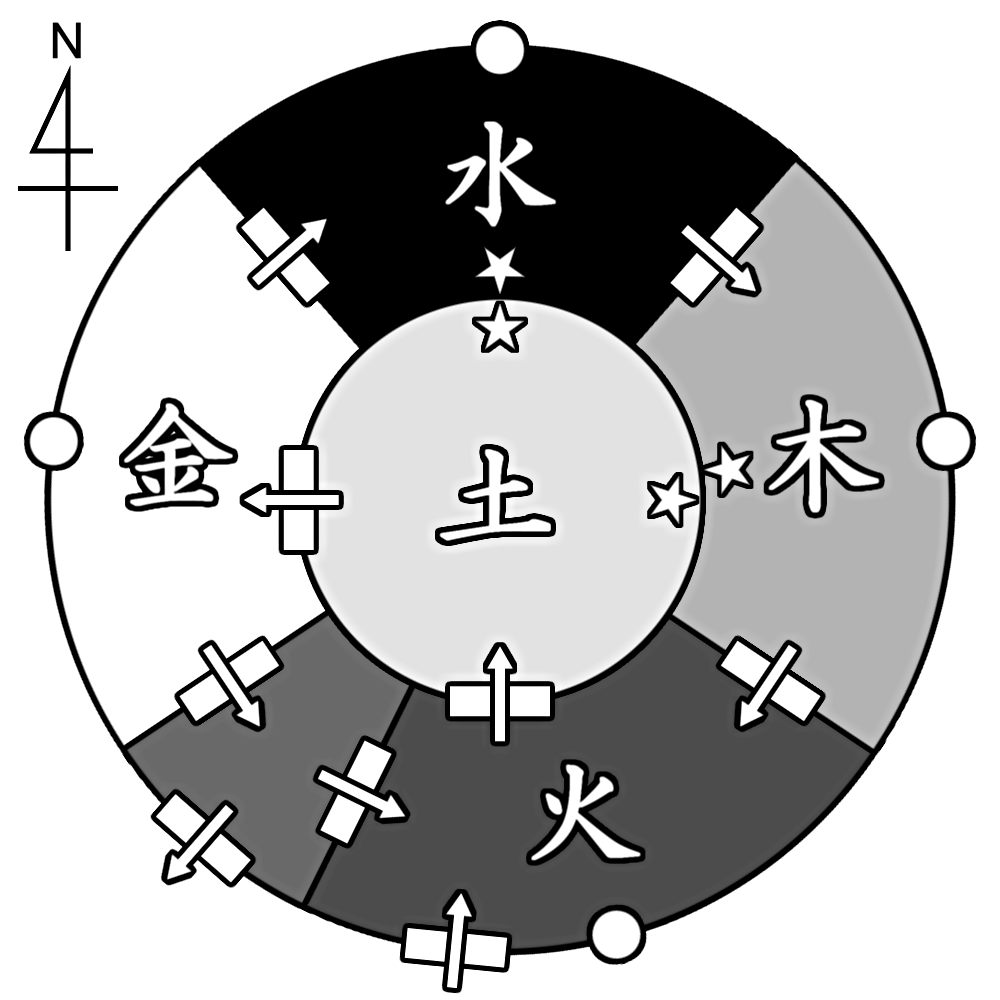
長々とやってきましたが、元の設定に戻ると、「AがBを生む」というのが「部屋Aから部屋Bに移動できる」に対応しているのでした。ということは、この結果から、金から第6の部屋に行くことができるということになります。

作中では金の部屋にあったクローゼットの裏に扉があり、そこから第6の部屋に行くことができる、という設定としています。第6の部屋は外では?と言われればそうなんですが、そうすると窓から脱出ということになり伏線が面倒なことになりそうだったので聞かなかったことにします。

ということで、本来の部屋の配置はこうなっていたのでした。普通に考えたら気づくのでは?という指摘も認めません。

他の解

さて、ここまで読んで少し引っかかりを覚えた方がいるかも知れません。

実は、最後の証明では「要素が6つしかない」ということを仮定していました。この仮定をなくし、単に6つ目の要素が存在することだけを仮定しても問題なさそうな気もします。

これを外す、つまりcomplete_6を認めないことにします。この場合、先の証明のパターンマッチではcomplete_6を使っていたので、それが使えません。すると、金がnewを生むことも、火がnewを生むことも示せなくなってしまいます。これはなぜでしょうか。

条件「各要素は必ずあるものを生み、あるものによって生まれるが、自分自身を生むことはない」をよく見ると、6つ目の要素の存在だけが仮定されている場合、7つ目の要素の存在は否定されません。これをnew2とすると、newがnew2を生み、new2がnewを生む、という関係が成り立つかもしれません。ということは、火土金水木については相生関係のみが成り立ち、newとnew2についてはこの関係のみが成り立つ、としても何ら矛盾しないわけです。

つまり、新しい要素についての条件を課さずに火土金水木のいずれかから新しい要素を必ず生めるのは、要素が6個の場合に限られます。

冒頭の論理パズルに対する解には「第6の要素newと第7の要素new2が存在し、金がnewを生み、newがnew2を生み、new2が火を生む」も含まれますが、「5つの要素以外が存在すれば、そのうち少なくとも一つは火土金水木のいずれかから生まれる」という論理パズルに解が存在するための条件以外に新しい要素に対して条件を課さないという制約の元では、これは解になりえません。

さて、このように断言したからには、このことを示す必要があります。示すべき主張は、「要素が相異なるとき、要素数が6個とは限らなければ(complete_6がなければ)、火土金水木以外の要素のうち火土金水木のいずれからも生まれないようなものの存在を否定できない」となります。つまりそのような反例モデルを一つ与えればよいです。

※思った以上に時間がかかったのでここは演習問題とします。多分後日更新します。

おわりに

Leanを用いて論理パズルの証明ができました。

本当はこの論理パズルの背景とかも書きたかったのですが、いかんせん時間がかかりすぎて他のタスクがこちらを睨んできているので、ひとまずここで締めさせていただきます。

1. 東京大学理学部情報科学科の学部生(一部は内定した教養学部前期課程2年生)らによるAdvent Calendarです。 ↩

2. 記事の公開日を見て分かる通り、当初は12/5の記事としての執筆は予定していませんでした。しかしながら、学科同期の「過ぎた日でも良いから埋めてほしいな～」といった発言を受け、重い腰を上げてこの日³を選びました。なお、本来は過去の日付ではなく未来の日付に入れるつもりだったのですが、期限を区切って書くと多分間に合わないことが予想されたため、過去の日付を選ぶことにしました。 ↩

3. さらに余談ですが、12/5は私の誕生日です。毎年アドカレの時期はどこかで12/5の記事を書くことにしていたのですが、今年は既に別の団体で執筆予定であった(&テーマが思いつかなかった)ため見送っていました。 ↩ ↩²

4. 最初は漠然とCoqで証明しようかなぁと思っていたのですが、理学部ガイダンス(駒場1年生向け)においてLeanを知っている一年生がいて刺激を受けたため、Leanを採用しました。 ↩

5. なんと、ABC予想の証明の成否をLeanで示そうという動きもあるようです。 ↩

6. 狭義には同人サークルである上海アリス幻樂団が制作する著作物のことを指しますが、有志による二次創作作品なども含めたコンテンツ全体を指すことも多いです。二次創作に寛容であることで知られています。 ↩

7. この原稿は所属団体の合同誌『東大幻想郷弐拾肆』に掲載されています。 ↩

8. 今回のパズルでは排中律を使っていないので直観主義論理の範囲でも解が求められるはずです。 ↩

9. 拡張性の高いフリー動画編集ソフト。画像編集ソフトとしても使われます。今年久々に作者のサイトが更新され、AviUtl2が公開されました。 ↩

10. MathJaxで縦並べをどうやるかが分からなかったのでTypstでかきました。Typstならgridでできるんですが……。 ↩