Problem
Fibonacci数列を求める問題です。
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
InputとOutputの例は次になります。
Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Key Idea
大きく分けて、f(n) → f(n-1) → f(n-2) ... と考えていくTop-downの方法と、f(1) → f(2) → f(3) ...と考えていくBottom-upの方法があります。
Approach 1 : Top-down Approach (Recursion)
このアプローチでは、問題(n番目のフィボナッチ数を求めること)を部分問題(n-1番目とn-2番目のフィボナッチ数を求めること)に分解します。n番目から考え始めるのでTop-downアプローチと呼ばれます。再帰を使用してこれを実現します。
class Solution:
def fib(self, n: int) -> int:
if n <= 1:
return n
else:
return self.fib(n-1) + self.fib(n-2)
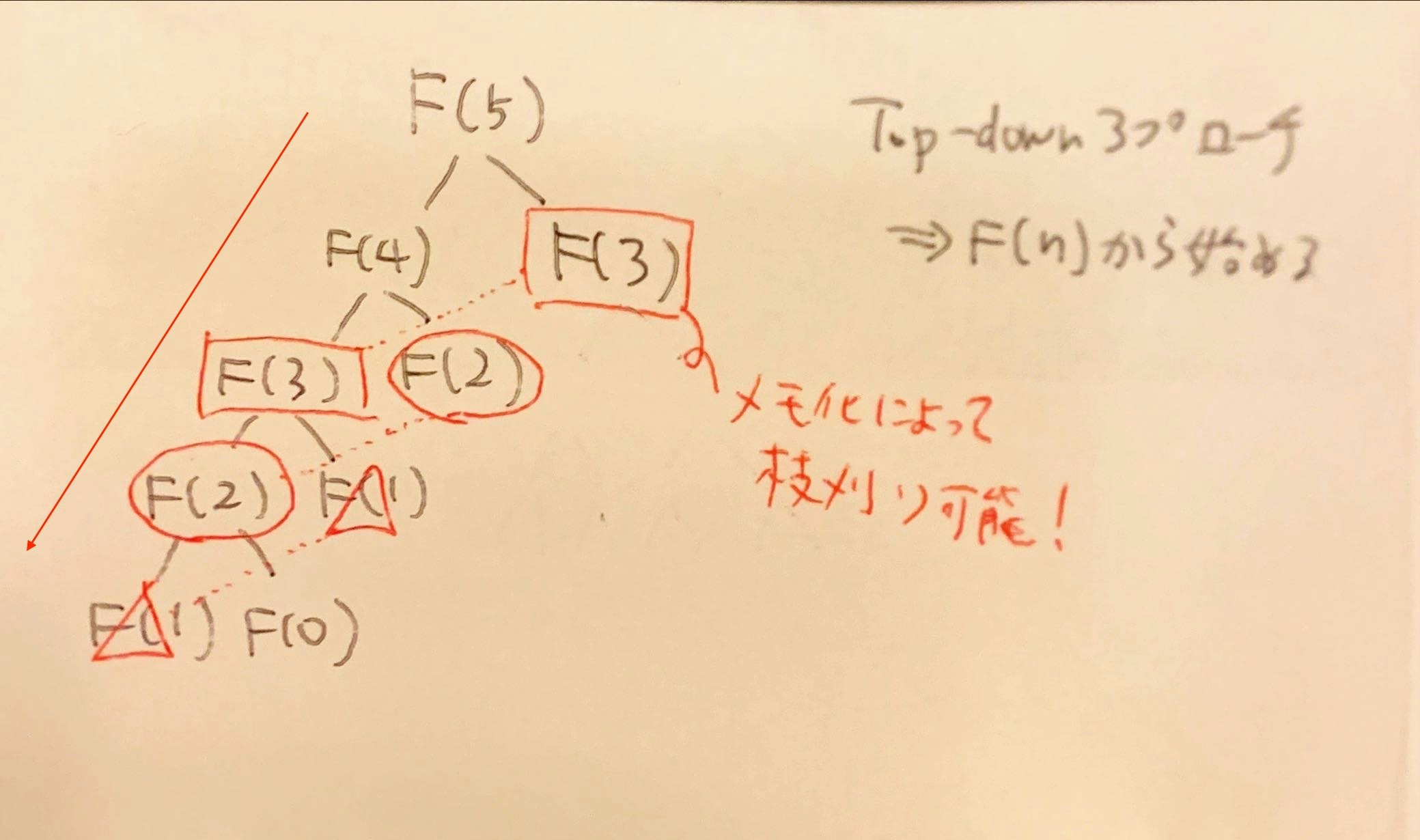
Approach 2: Top-Down Approach using Memoization
このアプローチでは、再帰を使用してフィボナッチ数を求めますが、計算を高速化するために「メモ化」も使用します。メモ化とは、以前計算した結果を保存して再利用することで、同じ計算を繰り返さないようにする方法です。
class Solution:
memo = {0:0, 1:1}
def fib(self, n: int) -> int:
if n in self.memo:
return self.memo[n]
else:
self.memo[n] = self.memo[n-1] + self.memo[n-2]
return self.memo[n]
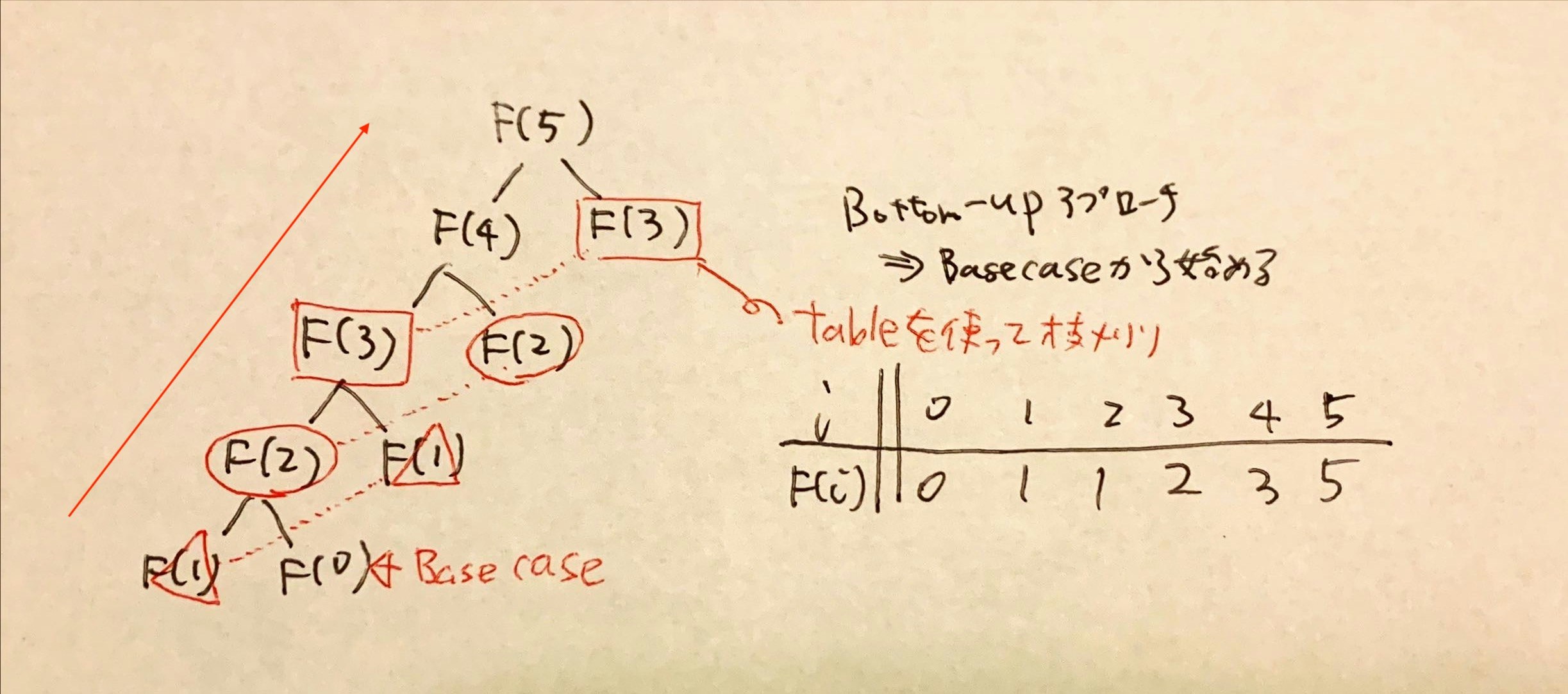
Approach #3 Bottom-Up Approach using Tabulation
このアプローチでは、0からnまでのフィボナッチ数を順番に計算します。途中の結果を配列に保存し、新しいフィボナッチ数を計算する際に以前の結果を再利用します。
class Solution:
def fib(self, n: int) -> int:
memo = []
memo.append(0)
if n >= 1:
memo.append(1)
for i in range(2,n+1):
memo.append(memo[i-1] + memo[i-2])
return memo[n]
Approach #4 Iterative Bottom-Up Approach
この解き方は、Approach 3と同じくBottom-upの方法です。ただし、テーブル全体をメモリに保持することなく、必要な直前の2つのフィボナッチ数だけを保持する方法を採用しています。そのため、メモリの節約が期待できます。
class Solution:
def fib(self, n: int) -> int:
if n == 0:
return 0
elif n == 1:
return 1
prev_1 = 1
prev_2 = 0
for i in range(2,n+1):
current = prev_1 + prev_2
prev_2 = prev_1
prev_1 = current
return current
Complexity Analysis
計算量は下記の様になります。
| Approach | Time complexity | Space complexity |
|---|---|---|
| 1. Top-down Approach (Recursion) | O(2^n) | O(n) |
| 2. Top-Down Approach using Memoization | O(n) | O(n) |
| 3. Bottom-Up Approach using Tabulation | O(n) | O(n) |
| 4. Iterative Bottom-Up Approach | O(n) | O(1) |
Reference