Numpyとの比較で学ぶJuliaのベクトル・行列の記法

Abstract

Juliaのベクトル・行列とNumpy.ndarrayの記法を比較してまとめました。(備忘録)

本記事では主にPythonのNumpyをよく使っていた人を対象に、「Juliaではこうやって書く」を紹介することになります。
とはいえ、記事を書いている本人はJuliaを初めて1ヶ月も経っていないので、間違いなどありましたら指摘してもらえたら嬉しいです。

環境・前提

• OS: Windows 10
• Python: 3.7.9
• Numpy: 1.20.3
• Julia: 1.6.2

Pythonのコードではimport numpy as npを前提にします。
Juliaでは以下のパッケージを用いることがあります。

• LinearAlgebra
• Statistics

必要ならPkg.addしてください。
標準でした。

また文法についてはほぼ触れません。

indexのスタート

Numpy(Python)ではインデックスは0スタートです。
一方でJuliaでは1スタートです。地味に注意。

1次元(Vector)

1次元の場合、indexの始まりに注意すれば問題ならないかと。

宣言・初期化

JuliaではNumpy.array()みたいなのは使わない
Arrayコンストラクタで作ることはできるが・・使うのかなぁ？
→ Vector(iter)などはメモリ効率の観点で禁忌というコメントを頂きました！

ベクトル宣言.jl

julia> x = [1, 2, 3]
3-element Vector{Int64}:
 1
 2
 3


# 各要素が0で長さが4のベクトル。型はFloat64がデフォルト。
julia> x = zeros(4)
4-element Vector{Float64}:
 0.0
 0.0
 0.0
 0.0

# 各要素の型がInt8で値が0、長さ5のベクトル
julia> x = zeros(Int8, 5)
5-element Vector{Int8}:
 0
 0
 0
 0
 0

julia> x = ones(5)
5-element Vector{Float64}:
 1.0
 1.0
 1.0
 1.0
 1.0


# このような用途ではcollectは非推奨！！次の小セクション参照。
# start:end を使って等差数列(交差は1) Pythonのrangeと異なり、endを含む点は注意。
julia> x = collect(0:5)
6-element Vector{Int64}:
 0
 1
 2
 3
 4
 5

# start:step:end で生成
julia> x = collect(0:2:5)
3-element Vector{Int64}:
 0
 2
 4

ones, zerosの他にも色々ある。引数は上記と変わらない。
なおMatrixでも次元の指定部分を変えるだけ。

関数	返り値
trues	各要素がtrue
falses	各要素がfalse
rand	各要素が区間[0, 1)から生成される乱数(各要素は無相関)
randn	各要素が標準正規分布から生成される乱数(各要素は無相関)

また、C言語っぽく初期化されていないベクトルはVector{T}(undef, ndims)で作れる。
similar(array)関数を使えば、初期化されていないベクトル/行列を取得できる。これはNumpyにはない気がする(要出典)。

ベクトル宣言2.jl

# 型の指定なしでも宣言できるが、恐らくこれは悪手。Any型が良いわけない(偏見)。
julia> a = Vector(undef, 3)
3-element Vector{Any}:
 #undef
 #undef
 #undef

# 不定値が3成分並んだVectorができた。
julia> a = Vector{Float64}(undef, 3)
3-element Vector{Float64}:
 1.75941583e-315
 1.321394854e-315
 1.32155256e-315

# similarでaと同じサイズの不定値のベクトル生成
julia> b = similar(a)
3-element Vector{Float64}:
 1.424476236e-315
 1.424476236e-315
 1.424476236e-315

参考：黒木先生による紹介ツイート

[重要] collect(iter), Vector(iter)について

Vectorはcollect, Vectorでも作成できるが、0:5, 0:2:5のままの方がメモリを無駄に使わず、結果的に高速化するとのこと。

julia> x = 0:5
0:5

# 型は UnitRange
julia> typeof(x)
UnitRange{Int64}

# これは AbstractVector を継承している！
julia> UnitRange <: AbstractVector
true

julia> y = 1:6
1:6

# 行列・ベクトルとして演算可能(演算の詳細は後述)
julia> x'y
70

またVectorとcollectでは、基本的にcollectを用いる方がよいとのこと。np.ndaaray(iter)じゃなくてnp.array(iter)するみたいな感じでしょう。またジェネレータなどはcollectは上手く動作する一方で、Vectorはうまく動作しない事例もあるそうだ。

julia> gen = (x^2 for x in 1:4)
Base.Generator{UnitRange{Int64}, var"#1#2"}(var"#1#2"(), 1:4)

# ジェネレータはベクトル扱いできない
julia> typeof(gen) <: AbstractVector
false

# collectはベクトルに変換できる
julia> collect(gen)
4-element Vector{Int64}:
  1
  4
  9
 16

# Vectorはエラー
julia> Vector(gen)
ERROR: MethodError: no method matching (Vector{T} where T)(::Base.Generator{UnitRange{Int64}, var"#1#2"})

このように等差数列のVector生成はUnitRange型のstart:step:endで行い、どうしても使うのなら汎用性の観点でcollect(iter)を使うべし。

黒木先生からのご指摘によります。感謝申し上げます。

length, size, shape

Numpyお馴染みのアトリビュート達。

長さとか.py

>>> x = np.array([1, 2, 3])

>>> len(x)
3
>>> x.shape
(3, )
>>> x.size
3

Juliaはshapeに相当するものがsize()だと思われる。
shape()はなさそう？(要出典)

長さとか.jl

julia> x = [1, 2, 3]

julia> length(x)
3
julia> size(x)
(3,)

なお、Pythonではxは1次元numpy配列であって、2次元numpy配列とは異なる。
一方でJuliaでは1次元配列は通常縦ベクトルで扱われる。
詳しくは後半の行列の演算で述べる。

基本的なアクセス

ここは簡単。

アクセス.py

>>> x = np.array([1, 2, 3])

>>> x[0]
1
>>> x[1]
2
>>> x[3]
3

# 末尾のアクセスは-1で可能
>>> x[-1]
3

アクセス.jl

julia> x = [1, 2, 3]

julia> x[1]
1
julia> x[2]
2
julia> x[3]
3

# Juliaでは末尾のアクセスにはendというキーワード？を用いる。
julia> x[end]
3

Pythonではお馴染みのスライスもJuliaではサポートしている。

スライス.py

>>> a = np.array([1, 2, 3, 4, 5])

>>> a[1:3]
array([2, 3])
>>> a[2:]
array([3, 4, 5])

indexの違いにより、同じ結果を得るためにはスライスのindexに注意しなければならない。

スライス.jl

julia> a = 1:5;

julia> a[2:3]
2-element Vector{Int64}:
 2
 3

# Pythonと違い、最後の成分の省略はエラー
julia> a[3:]
ERROR: syntax: missing last argument in "3:" range expression

# endで最後の指定をする
julia> a[3:end]
3-element Vector{Int64}:
 3
 4
 5

イテレーション

Juliaは単純なイテレーションでも色々あるらしい。

イテレーション.py

x = np.array([1, 2, 3])

for i in range(x.shape[0]):
    print(x[i])

'''
1
2
3
'''

イテレーション.jl

x = [1, 2, 3]

for i in 1:length(x)
    println(x[i])
end

#=
1
2
3
=#

# ドキュメントではこっちの方が推奨？
for i in eachindex(x)
    println(x[i])
end

#=
1
2
3
=#

Juliaのイテレーションについては、逆引きJulia 配列要素の参照、色々 及び 黒木先生の紹介ツイートが詳しい。

基本演算

Numpyでは、形状が同じなら、基本的には要素ごとの演算で+各種演算子が定義されている。

演算.py

>>> x = np.array([1, 2, 3])
>>> y = np.array([7, 8, 9])

>>> x + y
np.array([ 8 10 12])
>>> x - y
np.array([-6 -6 -6])
>>> x * y
np.array([ 7 16 27])
>>> x / y
np.array([0.14285714 0.25       0.33333333])
>>> x ** y
np.array([    1   256 19683])

一方で、Juliaでは各要素に対する演算は、.を各種演算子に付け加えることで実現する。

演算.jl

julia> x = [1, 2, 3];
julia> y = [7, 8, 9];

julia> x .+ y
3-element Vector{Int64}:
  8
 10
 12

julia> x .- y
3-element Vector{Int64}:
 -6
 -6
 -6


julia> x ./ y
3-element Vector{Float64}:
 0.14285714285714285
 0.25
 0.3333333333333333

julia> x .* y
3-element Vector{Int64}:
  7
 16
 27

julia> x .^ y
3-element Vector{Int64}:
     1
   256
 19683

なお、関数に対しても同様に.を必要とする。

関数.jl

julia> x = [1, 2, 3];
julia> f(x) = x^2 + 1
f (generic function with 1 method)

# 関数の次に . をつけることで、作用を各要素にする
julia> f.(x)
3-element Vector{Int64}:
  2
  5
 10

# `@.`マクロを使えばその行の関数を全て各要素に作用するようにできる。
julia> @. sin(cos(x))
3-element Vector{Float64}:
  0.5143952585235492
 -0.4042391538522658
 -0.8360218615377305

Numpyでの内積はこんな感じ。
2次元ndarrayとして扱う場合は以下の方法ではダメ。

内積.py

>>> x = np.array([1, 2, 3])
>>> y = np.array([7, 8, 9])

>>> np.dot(x, y)
50

Juliaではdot関数のあるLinearAlgebraパッケージが必要。(標準パッケージ)

内積.jl

>>> using LinearAlgebra

>>> x = [1, 2, 3];
>>> y = [7, 8, 9];

>>> dot(x, y)
50

# 転置 ' を使えば以下でも可能。
>>> x'y
50

比較

Numpyでは、==, !=演算子によってTrue, FalseのNumpy配列が返却される。
なお以下の議論は大体==で行うが、!=, >, <, >=, <=などでも同じ。

比較.py

>>> a = np.array([1, 2, 3])
>>> b = np.array([3, 2, 1])

>>> a == 1
array([ True, False, False])
>>> a == b
array([False,  True, False])

# サイズが違うと怒られる。
>>> c = np.array([1, 2, 3, 4])
>>> a == c
__main__:1: DeprecationWarning: elementwise comparison failed; this will raise an error in the future.
False

Juliaでは、前項同様に.==を用いるようだ。
==によってエラーを吐かないっぽい(オブジェクトの等価性を評価している？)ので、注意が必要かもしれない。

比較.jl

julia> a = [1, 2, 3];
julia> b = [3, 2, 1];

# 各要素と右辺の2を比較
julia> a .== 2
3-element BitVector:
 0
 1
 0

# これはエラーにならず、falseが返ってくることに注意。むしろエラーしてくれ？
julia> a == 2
false

# Vector同士でも==の比較ができてしまう。全要素が等しいかを比較している？
julia> a == b
false

# .==を使うと、Numpyみたいな結果が得られる。
julia> a .== b
3-element BitVector:
 0
 1
 0

Numpy同様、all, anyもある。

比較2.jl

# all, anyはNumpyっぽく使える。ただしBitVectorでないとエラーを吐く。
julia> all(a)
ERROR: TypeError: non-boolean (Int64) used in boolean context

# .==, .>等で比較した結果の配列を渡す
julia> all(a .> 2)
false

# anyも同様
julia> any(a .== 2)
true

上記の方法はNumpyっぽくて読みやすい気がするが、実のところこれよりも優れた方法がある。

all(f, iter)のように、関数(或いは演算)を渡すことで高速化する。

比較3.jl

# 比較演算子単体で関数が作れるとは・・・`> (2)` のようにスペースを空けるとエラー。
julia> >(2)
(::Base.Fix2{typeof(>), Int64}) (generic function with 1 method)

# それを利用して実行。
julia> all(>(2), a)
false

BenchmarkTools.jlを用いて確認してみる。

julia> using BenchmarkTools

julia> a = 1:100000
1:100000

julia> @benchmark all(a .> 2)
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
 Range (min … max):  36.700 μs …  4.982 ms  ┊ GC (min … max): 0.00% … 98.88%
 Time  (median):     40.400 μs              ┊ GC (median):    0.00%
 Time  (mean ± σ):   44.334 μs ± 70.445 μs  ┊ GC (mean ± σ):  2.20% ±  1.40%

  █
  █▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁  ▁ ▁ ▁
  63.3 μs         Histogram: frequency by time        38.9 μs <

 Memory estimate: 16.69 KiB, allocs estimate: 6.

julia> @benchmark all(>(2), a)
BenchmarkTools.Trial: 10000 samples with 398 evaluations.
 Range (min … max):  236.683 ns …   4.349 μs  ┊ GC (min … max): 0.00% … 92.46%
 Time  (median):     262.814 ns               ┊ GC (median):    0.00%
 Time  (mean ± σ):   285.118 ns ± 104.296 ns  ┊ GC (mean ± σ):  0.64% ±  2.07%

                                                              ▅ █
  ▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▂▁▁▁▁▁▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁█ █
  248 ns           Histogram: frequency by time          250 ns <

 Memory estimate: 64 bytes, allocs estimate: 2.

all(BitVector?)よりall(f, iter)の方が今回の例では圧倒的に早い+メモリの使用量が少ないという結果が得られた。
これは後々登場するsumなどでも同じで、sum(f.(a))よりもsum(f, a)の方が圧倒的に高速に動作するようだ。

最大最小

Numpyではmin, maxでおｋだった。

最大最小.py

>>> x = np.array([1, 5, 4, 9, -2])

>>> np.min(x)
-2
>>> np.max(x)
9

一方でJuliaの場合、最大最小に関する組み込み関数が2種類ある。
Juliaで配列の最小値を計算する時はminよりminimumの方が圧倒的に速いです!!の検証結果及びコメント欄を参考にしてほしい。なおnp.minimum, np.maximumとは名前が同じだけで、全く動作は異なるので注意。

最大最小.jl

julia> x = [1, 5, 4, 9, -2];

# こっちの方が良い？
julia> minimum(x)
-2
julia> maximum(x)
9

# min()でも可能だが、...を使って展開する必要がある。展開が遅いらしいので非推奨？(上記記事のコメント欄参照)
julia> min(x...)
-2
julia> max(x...)
9

ソート

Numpyではnp.sortを使えばヨシ。indexのソートを返すargsortの例も置いておく。
x.sort()だと自身を書き換える破壊的メソッドなので注意。

ソート.py

>>> x = np.array([1, 5, 4, 9, -2])

>>> np.sort(x)
np.array([-2  1  4  5  9])

# 降順の場合はスライスで反転させる。
>>> np.sort(x)[::-1]
np.array([ 9  5  4  1 -2])

# argsort
>>> np.argsort(x)
np.array([4 0 2 1 3])

Juliaでもsort関数が定義されている。
また、indexの結果を返すnp.argsort的なものもちゃんとある。
sort!関数では引数の配列をソートする破壊的メソッドなので注意。

ソート.jl

julia> x = [1, 5, 4, 9, -2];

julia> sort(x)
(x) = [-2, 1, 4, 5, 9]

julia> sort(x, rev=true)
5-element Vector{Int64}:
 -2
  1
  4
  5
  9

# 便利機能。byに関数を渡して、その値でソートできる。
julia> sort(x, by=abs)
5-element Vector{Int64}:
  1
 -2
  4
  5
  9

# このsortpermがargsortに相当する。
perm = sortperm(x)
5-element Vector{Int64}:
 5
 1
 3
 2
 4

# indexの並び替えを指定した配列を使えば、それに従って並び替えることができる。
julia> x[perm]
5-element Vector{Int64}:
 -2
  1
  4
  5
  9

統計的な量

単純な和、平均値や分散など。
Numpyではnp.mean等が用意されていた。

統計.py

>>> x = [1, 5, 4, 9, -2]

>>> np.sum(x)
17

>>> np.mean(x)
3.4

>>> np.std(x)
3.7202150475476548

一方で、Juliaの場合はStatisticsパッケージが必要となる。(標準パッケージ)

統計.jl

julia> using Statistics

julia> x = [1, 5, 4, 9, -2];

# sumは組込み関数。
julia> sum(x)
17

# 平均
julia> mean(x)
3.4

# 標準偏差
julia> std(x)
4.159326868617084

Statisticパッケージは、その他便利な機能が沢山あるようなので、ドキュメントを読んでみるとよいだろう。

2次元(Matrix)

宣言・初期化

NumpyではPythonの2次元配列→Numpyの2次元配列(行列)といった風に作成する。
全要素が0, 1の配列はnp.zeros, np.onesを使うし、単位行列はnp.eye, np.identityを使う。

宣言初期化.py

>>> A = np.array([[1, 2, 3], [4, 5, 6]])
>>> A
array([[1, 2, 3],
       [4, 5, 6]])
>>> B = np.zeros((2, 3))
>>> B
array([[0., 0., 0.],
       [0., 0., 0.]])
>>> I = np.identity(3)
>>> I
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

Juliaでは2次元配列はデフォルトで行列となっている(要出典)。
行列の宣言に注意すれば、生成する関数はVectorの場合とほぼ同様。形状を指定する引数ndimを変えればよい。
また単位行列はLinearAlgebraパッケージに定数Iとして存在している。

宣言初期化.jl

julia> A = [1 2 3; 4 5 6]
2×3 Matrix{Int64}:
 1  2  3
 4  5  6

# 形は順番に引数に渡してもよいし
julia> B = zeros(2, 3)
2×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0

# タプルの形で渡してもよい
julia> C = ones((3, 3))
3×3 Matrix{Float64}:
 1.0  1.0  1.0
 1.0  1.0  1.0
 1.0  1.0  1.0

julia> using LinearAlgebra

# Iは単位行列かのようにふるまう
julia> C + I
3×3 Matrix{Float64}:
 2.0  1.0  1.0
 1.0  2.0  1.0
 1.0  1.0  2.0

# 正方行列と演算しないとエラー
julia> A + I
ERROR: DimensionMismatch("matrix is not square: dimensions are (2, 3)")

Vectorの初期化でも紹介したtrues(), falses()なども同様に使える。
また、Juliaでは初期化されていない行列もVector同様生成できる。

宣言初期化2.jl

# 型は指定する方が良いと思われる。
julia> A = Matrix{Float64}(undef, 2, 3)
2×3 Matrix{Float64}:
 2.25424e-315  2.25424e-315  1.42334e-315
 1.42409e-315  2.27212e-315  2.25708e-315

# similarで型・サイズが同じ初期化されていない行列を生成
julia> B = similar(A)
2×3 Matrix{Float64}:
 6.36599e-314  4.24399e-314  1.0e-323
 4.24399e-314  1.061e-313    2.53777e-315

# Aと同じサイズで、型は整数にするとき
julia> C = similar(A, Int64)
2×3 Matrix{Int64}:
  288317200  288317200  288317200
 2371464384  288317200  288317200

# なお、similarを用いれば `undef`なしで書ける
julia> A = similar(zeros(), Int64, 3, 4)
3×4 Matrix{Int64}:
         4          7     7     8
         1          1     1     1
 288317184  288317185  -256  -255

上記のsimilar()のテクニックはVectorでも使えるため、覚えておきたい。

length, size, shape

Numpyでお馴染みのshape, size。

長さとか.py

>>> A = np.zeros((2, 2))
>>> A
array([[0., 0.],
       [0., 0.]])
>>> len(A)
2
>>> A.shape
(2, 2)
>>> A.size
4

Vectorの時と同様。
Matrixの場合lengthは要素の数で、sizeが2×2などの形状を返す。

長さとか.jl

julia> A = zeros((2, 2))
2×2 Matrix{Float64}:
 0.0  0.0
 0.0  0.0

julia> length(A)
4

julia> size(A)
(2, 2)

reshape

Numpyでもshapeを変換するためにnp.reshape, ndarray.reshapeを使えた。

reshape.py

>>> A = np.array([[1, 2, 3], [4, 5, 6]])
>>> A
array([[1, 2, 3],
       [4, 5, 6]])
>>> B = np.reshape(A, (3, 2))
>>> B
array([[1, 2],
       [3, 4],
       [5, 6]])

Juliaでは組込みでreshape関数がある。
またJuliaの多くの関数では、形状を指定する際タプルで渡してもよいし、順番に引数に渡してもよい(可変長引数)のはNumpyとの大きな違いであろう。

reshape.jl

# ones((2, 3))でもよい
julia> A = ones(2, 3)
2×3 Matrix{Float64}:
 1.0  1.0  1.0
 1.0  1.0  1.0

# reshape(A, 3, 2)でもよい
julia> B = reshape(A, (3, 2))
3×2 Matrix{Float64}:
 1.0  1.0
 1.0  1.0
 1.0  1.0

基本的なアクセス

Numpyの場合は、基本的にはA[行][列]の形でアクセスし、A[行]では列が返ってきた。またスライスの利用で行も取得できた。

アクセス.py

>>> A = np.array([[1, 2, 3], [4, 5, 6]])
>>> A
array([[1, 2, 3],
       [4, 5, 6]])

# 要素のアクセス
>>> A[0][1]
2

# 列のアクセス
>>> A[0]
array([1, 2, 3])
>>> A[1]
array([4, 5, 6])

# 行のアクセス
>>> A[:, 0]
array([1, 4])

一方でJuliaでも色々アクセスの仕方がある。
最も基本的なアクセスの仕方は、Vectorのようなアクセス方法と、行と列で指定する2種類がある。
それぞれLinear indexing, Cartesian indexingと呼ぶらしい。

アクセス.jl

julia> A = [1 2 3; 4 5 6]
2×3 Matrix{Int64}:
 1  2  3
 4  5  6

# Numpyと違い、要素が返ってくる
julia> A[1]
1

# しかも列指向であるので、2ではなく4が返ってくる！
julia> A[2]
4

# [行, 列]で指定すると、Numpyっぽい
julia> A[1, 2]
2

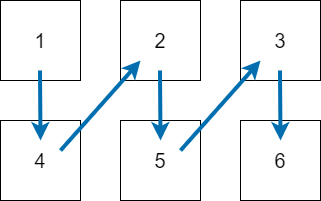
列指向を完全に理解しているわけではないが、今回の行列の場合以下のような順番になる。

よってA[3] = 2であり、`A[4] = 5, A[5] = 3, A[6] = 6となる。

イテレーション

Numpyでfor文ってよく考えたら速度的にNGだった気が
Numpyでは単純にやると行ごとにイテレーションする。

イテレーション.py

A = np.array([[1, 2, 3], [4, 5, 6]])

for a in A:
    print(f"a = {a}, type: {type(a)}")

'''
a = [1 2 3], type: <class 'numpy.ndarray'>
a = [4 5 6], type: <class 'numpy.ndarray'>
'''

一方でJuliaでは成分ごとに、列指向の順でイテレーションされる。
ちなみにJuliaでは場合によってはforで計算する方が速いこともあるとか(要出典)。

イテレーション.jl

A = [
    1 2 3;
    4 5 6
]

for a in A
    println("a = $(a), type: $(typeof(a))")
end
#=
a = 1, type: Int64
a = 4, type: Int64
a = 2, type: Int64
a = 5, type: Int64
a = 3, type: Int64
a = 6, type: Int64
=#

その他にも、色々とイテレーションの方法はある。

イテレーション2.jl

# 列ごとにイテレーション
for a in eachcol(A)
    println("a = $(a), type: $(typeof(a))")
end

#=
a = [1, 4], type: SubArray{Int64, 1, Matrix{Int64}, Tuple{Base.Slice{Base.OneTo{Int64}}, Int64}, true}
a = [2, 5], type: SubArray{Int64, 1, Matrix{Int64}, Tuple{Base.Slice{Base.OneTo{Int64}}, Int64}, true}
a = [3, 6], type: SubArray{Int64, 1, Matrix{Int64}, Tuple{Base.Slice{Base.OneTo{Int64}}, Int64}, true}
=#

# 行ごとにイテレーション
for a in eachrow(A)
    println("a = $(a), type: $(typeof(a))")
end

#=
a = [1, 2, 3], type: SubArray{Int64, 1, Matrix{Int64}, Tuple{Int64, Base.Slice{Base.OneTo{Int64}}}, true}
a = [4, 5, 6], type: SubArray{Int64, 1, Matrix{Int64}, Tuple{Int64, Base.Slice{Base.OneTo{Int64}}}, true}
=#

# indexを順番にイテレーション
for a in eachindex(A)
    println("a = $(a), type: $(typeof(a))")
end
#=
a = 1, type: Int64
a = 2, type: Int64
a = 3, type: Int64
a = 4, type: Int64
a = 5, type: Int64
a = 6, type: Int64
=#

他にも様々な方法があるようだが、配列要素の参照、色々を参考にしてもらいたい。

基本演算

ここでは行列同士の演算を見ていく。
Numpyでは通常の演算子+, -等が使えた。

演算.py

>>> A = np.array([[1, 2, 3], [4, 5, 6]])
>>> B = np.array([[7, 8, 9], [9, 8, 7]])

# Numpyでは基本的には各要素同士の演算になる。
>>> A + B
array([[ 8, 10, 12],
       [13, 13, 13]])
>>> A - B
array([[-6, -6, -6],
       [-5, -3, -1]])
>>> A * B
array([[ 7, 16, 27],
       [36, 40, 42]])
>>> A / B
array([[0.14285714, 0.25      , 0.33333333],
       [0.44444444, 0.625     , 0.85714286]])
>>> A ** B
array([[     1,    256,  19683],
       [262144, 390625, 279936]], dtype=int32)

Juliaでは、+, -は通常の行列同士の足し算・引き算となる。
Vectorと同様に.+, .-などで各要素に同士の演算を行う。

演算.jl

julia> A = [1 2 3; 4 5 6];
julia> B = [7 8 9; 9 8 7];

# 行列同士の足し算
julia> A + B
2×3 Matrix{Int64}:
  8  10  12
 13  13  13

# 要素同士の足し算を強調？
julia> A .+ B
2×3 Matrix{Int64}:
  8  10  12
 13  13  13

# 行列同士の引き算
julia> A - B
2×3 Matrix{Int64}:
 -6  -6  -6
 -5  -3  -1

# 要素同士の引き算強調
julia> A .- B
2×3 Matrix{Int64}:
 -6  -6  -6
 -5  -3  -1

# *は行列の掛け算。今回の例(A, B)ではサイズが合わずにエラーとなる。
julia> A * B
ERROR: DimensionMismatch("matrix A has dimensions (2,3), matrix B has dimensions (2,3)")

# 要素同士の掛け算(アダマール積)は .* でできる。
julia> A .* B
2×3 Matrix{Int64}:
  7  16  27
 36  40  42

# A / B == A * inv(B) であるはずなのだが・・・(invは逆行列の計算)
julia> A / B
2×2 Matrix{Float64}:
 0.625   -0.375
 0.8125  -0.1875

# 要素同士の割り算
julia> A ./ B
2×3 Matrix{Float64}:
 0.142857  0.25   0.333333
 0.444444  0.625  0.857143

# 行列同士のべき乗は定義されていない
julia> A ^ B
ERROR: MethodError: no method matching ^(::Matrix{Int64}, ::Matrix{Int64})

# 要素同士のべき乗はできる。
julia> A .^ B
2×3 Matrix{Int64}:
      1     256   19683
 262144  390625  279936

Juliaでは要素同士の演算を.で強調できるのはNumpyと明確に異なる点であろう。
関数に対しても、Vectorと同様に.で要素同士の演算にできる。
ほぼ同じなのでここは省略します。

転置・トレース・行列式・逆行列

Numpyでは転置はndarray.Tで取得できた。
行列式などはnp.linalgモジュールを使えば良かった。

>>> A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> A
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
# 転置
>>> A.T
array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

# トレース
>>> np.trace(A)
15
# 行列式
>>> np.linalg.det(A)
0.0

# 逆行列
>>> B = np.identity(3)
>>> np.linalg.inv(B)
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

Juliaでは、転置は'或いはtranspose関数で可能。
またusing LinearAlgebraしておく。

julia> using LinearAlgebra

julia> A = Matrix(3*I, 3, 3)
3×3 Matrix{Int64}:
 3  0  0
 0  3  0
 0  0  3

# 転置
julia> A'
3×3 adjoint(::Matrix{Int64}) with eltype Int64:
 3  0  0
 0  3  0
 0  0  3

# transpose関数
julia> transpose(A)
3×3 transpose(::Matrix{Int64}) with eltype Int64:
 3  0  0
 0  3  0
 0  0  3

# tr関数でtraceを取得
julia> tr(A)
9

# 行列式もdet関数
julia> det(A)
27.0

# 逆行列はinv関数
julia> inv(A)
3×3 Matrix{Float64}:
 0.333333  0.0       0.0
 0.0       0.333333  0.0
 0.0       0.0       0.333333

eltypeは恐らくelement typeの略です。
'とtransposeの結果の型が微妙に違う気がする・・・。

他にも便利な機能が沢山あるため、Linear Algebraを読むとよいだろう。

比較

Numpyでは1次元同様、各要素を比較したTrue, FalseのNumpy配列を返すのだった。

比較.py

>>> A = np.array([[1, 2, 3], [4, 5, 6]])
>>> B = np.array([[3, 2, 1], [6, 5, 4]])

>>> A == B
array([[False,  True, False],
       [False,  True, False]])
>>> A < B
array([[ True, False, False],
       [ True, False, False]])

# サイズが違うと怒られるのではなく、単にFalseが返ってくる？エラー吐いてほしいな。
>>> C = np.ones((2, 2))
>>> A == C
False

Juliaでは、MatrixでもVectorと同じ挙動をする。
つまりNumpyのような要素同士の比較を行うには.==, .<などを用いる。

比較.jl

julia> A = [1 2 3; 4 5 6];
julia> B = [3 2 1; 6 5 4];

julia> A .== B
2×3 BitMatrix:
 0  1  0
 0  1  0

julia> A .< B
2×3 BitMatrix:
 1  0  0
 1  0  0

# 単純な == では、all(A .== B)と同じと思われる。
julia> A == B
false

# all, anyもVectorの時とほぼ同様。
julia> any(A .== 2)
true

最大最小

Numpyでもnp.max, np.minが使えた。
axisキーワードで軸に沿って最大最小を取得することもできた。

最大最小.py

>>> A = np.array([[1, 2, 3], [4, 5, 6]])

# 行方向に関して最小値
>>> np.min(A, axis=1)
array([1, 4])

# 列方向に関して最小値
>>> np.min(A, axis=0)
array([1, 2, 3])

# 全要素で最小値
>>> np.min(A)
1

Juliaでは、minimum, maximum関数のdimsキーワード引数によって軸に沿って最小最大を取得できる。
Numpyライクで良いですね。

最大最小.jl

julia> A = [1 2 3; 4 5 6];

# dims=1は列方向。
julia> minimum(A, dims=1)
1×3 Matrix{Int64}:
 1  2  3

# dims=2は行方向。
julia> minimum(A, dims=2)
2×1 Matrix{Int64}:
 1
 4

# 全体の最小値
julia> minimum(A)
1

# 最大値も同様である。
julia> maximum(A, dims=1)
1×3 Matrix{Int64}:
 4  5  6

なおVectorの際min(a...)といった記法があったが、行列に対してはA...がエラーになり、不可能であった。
展開は遅いらしいことを考慮すれば、素直にminimum, maximumでよいだろう。

ソート

Numpyのsortでもaxisキーワード引数で軸ごとにソートできた。

ソート.py

>>> A = np.array([[5, 1, 6], [4, 8, 2]])
>>> A
array([[5, 1, 6],
       [4, 8, 2]])

# axisを省略した場合はaxis=-1, 2次元ではaxis=1になる。
>>> np.sort(A)
array([[1, 5, 6],
       [2, 4, 8]])

# axis=1, つまり行方向にソート
>>> np.sort(A, axis=1)
array([[1, 5, 6],
       [2, 4, 8]])

# axis=1, つまり行方向にソートして逆順(降順)
>>> np.sort(A, axis=1)[:, ::-1]
array([[6, 5, 1],
       [8, 4, 2]])

# axis=0, つまり列方向にソート
>>> np.sort(A, axis=0)
array([[4, 1, 2],
       [5, 8, 6]])

# axis=0, つまり列方向にソートして逆順(降順)
>>> np.sort(A, axis=0)[::-1, :]
array([[5, 8, 6],
       [4, 1, 2]])

JuliaではVector同様sort関数を使う。
というか最大最小もソートもdims引数以外Vectorと同じである。

ソート.jl

julia> A = [5 1 6;
           4 8 2]
2×3 Matrix{Int64}:
 5  1  6
 4  8  2

# Numpyと違い、行列の場合はdimsの指定が必須なようだ。
julia> sort(A)
ERROR: UndefKeywordError: keyword argument dims not assigned

# dims = 1, つまり行方向にソート
julia> sort(A, dims=1)
2×3 Matrix{Int64}:
 4  1  2
 5  8  6

# 降順ソートは rev = trueで。 Numpyより簡単。
julia> sort(A, dims=1, rev=true)
2×3 Matrix{Int64}:
 5  8  6
 4  1  2

# dims = 2, つまり列方向にソート
julia> sort(A, dims=2)
2×3 Matrix{Int64}:
 1  5  6
 2  4  8

# 列方向にソート(降順)
julia> sort(A, dims=2, rev=true)
2×3 Matrix{Int64}:
 6  5  1
 8  4  2

また、Vectorの時同様byキーワードに関数を渡すことで、その返り値でソートできる。
なおVectorでも紹介したsortpermは行列では定義されていないらしい。
なんでだろう。

ソート2.jl

julia> B = [-5 1 6; 4 -8 2]
2×3 Matrix{Int64}:
 -5   1  6
  4  -8  2

# 二乗した値が大きい順に、列方向にソート
julia> sort(B, dims=1, by=x->x^2)
2×3 Matrix{Int64}:
  4   1  2
 -5  -8  6

# sortpermは行列では定義されていないらしい。
julia> sortperm(A, dims=1)
ERROR: MethodError: no method matching sortperm(::Matrix{Int64}; dims=1)

統計的な量

さすがにNumpy版の記述は飽きたので省略
Vector版のセクションと最大最小・ソートの際とほぼ同じ。

統計.jl

julia> A = [5 1 6;
           4 8 2]
2×3 Matrix{Int64}:
 5  1  6
 4  8  2

# 和：sum は dims 無指定では全成分の和
julia> sum(A)
26

# dims = 1, 列方向の和
julia> sum(A, dims=1)
1×3 Matrix{Int64}:
 9  9  8

# dims = 2, 行方向の和
julia> sum(A,dims=2)
2×1 Matrix{Int64}:
 12
 14

# 平均：mean はdims無指定で全要素の平均
julia> mean(A)
4.333333333333333

# dims = 1, つまり列方向の平均
julia> mean(A, dims=1)
1×3 Matrix{Float64}:
 4.5  4.5  4.0

# dims = 2, つまり行方向の平均
julia> mean(A, dims=2)
2×1 Matrix{Float64}:
 4.0
 4.666666666666667


# 標準偏差：std はdims無指定で全要素の標準偏差
julia> std(A)
2.581988897471611

# dims = 1, つまり列方向の標準偏差
julia> std(A, dims=1)
1×3 Matrix{Float64}:
 0.707107  4.94975  2.82843

# dims = 2, つまり行方向の標準偏差
julia> std(A, dims=2)
2×1 Matrix{Float64}:
 2.6457513110645907
 3.055050463303893

ベクトルと行列の演算

ここではVectorとMatrix同士の演算のNumpyと比較しながら見ていく。

Vectorの転置と行列のかけ算

Numpyの1次元配列は、良くも悪くもベクトル。

>>> x = np.array([1, 2, 3])
>>> A = np.array([[1, 0, 0], [1, 0, 1], [0, 1 ,1]])

# xは転置できない shapeが3 * 1 ではないため。
>>> x.shape
(3,)
>>> x.T.shape
(3,)

>>> y = A.dot(x)
>>> y
array([1, 4, 5])

>>> y = x.dot(A)
>>> y
array([3, 3, 5])

上記の計算結果は以下のように解釈できる。

    A.dot(x) = \begin{bmatrix}
        1 & 0 & 0  \\
        1 & 0 & 1  \\
        0 & 1 & 1
    \end{bmatrix} \begin{bmatrix}
        1  \\
        2  \\
        3  \\
    \end{bmatrix} = \begin{bmatrix}
        1  \\
        4  \\
        5  \\
    \end{bmatrix}

    x.dot(A) = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \begin{bmatrix}
        1 & 0 & 0  \\
        1 & 0 & 1  \\
        0 & 1 & 1
    \end{bmatrix}  = \begin{bmatrix} 3 & 3 & 5 \end{bmatrix}

いやまぁ・・・あのさぁ・・・

なお計算結果のy.shapeは両方同じで(3, )となる。
便利かも知れないが、少し気持ち悪い。勿論これを避けるには、reshapeで2次元配列として扱うようにすればよい。

一方でJuliaは基本的にVectorは縦ベクトルである。

julia> x = [1, 2, 3];
julia> A = [1 0 0; 1 0 1; 0 1 1]
3×3 Matrix{Int64}:
 1  0  0
 1  0  1
 0  1  1

# JuliaではVectorも転置できる。なぜなら縦ベクトルだから。
julia> x'
1×3 adjoint(::Vector{Int64}) with eltype Int64:
 1  2  3

# 想定通りの計算結果
julia> A * x
3-element Vector{Int64}:
 1
 4
 5

# これはエラー。
julia> x * A
ERROR: DimensionMismatch("matrix A has dimensions (3,1), matrix B has dimensions (3,3)")

# こっちは転置したから問題ない。返り値もしっかり1 * 3になっている。
julia> x' * A
1×3 adjoint(::Vector{Int64}) with eltype Int64:
 3  3  5

ベクトルと行列の演算では、あらかじめ縦ベクトルと割り切っているJuliaの方がミスを生み出しにくそうで好ましく感じた。

ブロードキャスト

Numpyでは、演算する際に形状が異なっていた時、適切に形状を変化させて演算する特徴がある。

ブロードキャスト.py

>>> A = np.zeros((3, 3))
>>> A
array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])
>>> a = np.array([1, 2, 3])

# aが縦にコピーされる
>>> A + a
array([[1., 2., 3.],
       [1., 2., 3.],
       [1., 2., 3.]])

Juliaでもそのような機能はある。Numpyと異なり、ベクトルは列(縦)ベクトルであるため、挙動が一見すると異なる。でもそこだけ注意すれば、Numpyと同じように扱えるであろう。

ブロードキャスト.jl

julia> A = zeros(3, 3)
3×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0

# カンマ区切りで宣言すると、これは縦ベクトル。
julia> a_vec = [1, 2, 3]
3-element Vector{Int64}:
 1
 2
 3

# 縦ベクトルが横にコピーされる
julia> A .+ a_vec
3×3 Matrix{Float64}:
 1.0  1.0  1.0
 2.0  2.0  2.0
 3.0  3.0  3.0

# スペースまたはtab区切りで宣言するとこれは行列。
julia> a_mat = [1 2 3]
1×3 Matrix{Int64}:
 1  2  3

# 縦にコピーされて足される
julia> A .+ a_mat
3×3 Matrix{Float64}:
 1.0  2.0  3.0
 1.0  2.0  3.0
 1.0  2.0  3.0

# ちなみに .+ じゃないとエラーになる。
julia> A + a
ERROR: DimensionMismatch("dimensions must match: a has dims (Base.OneTo(3), Base.OneTo(3)), b has dims (Base.OneTo(1), Base.OneTo(3)), mismatch at 1")

# 掛け算などでも同様。
julia> B = ones(3, 3)
3×3 Matrix{Float64}:
 1.0  1.0  1.0
 1.0  1.0  1.0
 1.0  1.0  1.0

julia> B .* a
3×3 Matrix{Float64}:
 1.0  2.0  3.0
 1.0  2.0  3.0
 1.0  2.0  3.0

ブロードキャストのルールはほとんどNumpyと同じ模様。
Numpyの便利ルールがそのまま使えるのはありがたい。

その他豆知識

Numpyとは関係ない、便利機能や補足のセクションです。

カンマ区切りやタブ・スペース区切りの違い

;区切りとスペース区切りは、ベクトル宣言と行列宣言の違いではないみたい。
;区切り→垂直に結合
スペース区切り→水平に結合
という意味。この説明はv1.6のArrayの公式ドキュメントによれば

If the arguments inside the square brackets are separated by semicolons (;) or newlines instead of commas, then their contents are vertically concatenated together instead of the arguments being used as elements themselves.

適当に和訳してみると、「[]の中で、セミコロン(;)または改行されているものは、垂直方向に結合されます。また仮にカンマ区切りであれば、そのまま要素として使われます。」
ふーん？以下のプログラム例が載っていた。

julia> [1:2, 4:5] # Has a comma, so no concatenation occurs. The ranges are themselves the elements
2-element Vector{UnitRange{Int64}}:
 1:2
 4:5

julia> [1:2; 4:5]
4-element Vector{Int64}:
 1
 2
 4
 5

julia> [1:2
        4:5
        6]
5-element Vector{Int64}:
 1
 2
 4
 5
 6

Similarly, if the arguments are separated by tabs or spaces, then their contents are horizontally concatenated together.

「同様に、タブやスペース区切りの場合は、水平方向に結合されます。」
なるほどね(?)以下も公式ドキュメントより。

julia> [1:2  4:5  7:8]
2×3 Matrix{Int64}:
 1  4  7
 2  5  8

julia> [[1,2]  [4,5]  [7,8]]
2×3 Matrix{Int64}:
 1  4  7
 2  5  8

julia> [1 2 3] # Numbers can also be horizontally concatenated
1×3 Matrix{Int64}:
 1  2  3

なるほど。

Vector, Matrix 扱いになる型

coming soon...

まとめ

Python, Numpy使っていた方が、Juliaでの演算の違いの参考になったら幸いです。

今後も間違い・非推奨な関数等が判明次第追記していきたいと思います。
またJuliaは非常に多くの型があるので、これらのNumpyの型との対応関係も調査できたら示していきたいです。

間違いなどありましたらコメント等よろしくお願いします。

参考資料等

• Juliaで最低限やっていくための配列操作まとめ
  • 演算以外の、配列操作に関する情報量と密度は随一かと。
• 逆引きJulia 配列要素の参照、色々
  • 行列のアクセスに関して、かなりの数を網羅している。
• 黒木先生による記事初版に対するコメント
  • 記事の間違いの指摘、ベストプラクティスの提示をしていただきました。