Juliaで最低限やっていくための配列操作まとめ

はじめに

新しくJuliaを始めた時に配列操作で困らない程度にまとめたものです(演算は含みません)。
量が多いので必要に応じて目次から飛ぶことをオススメします。

誤字脱字、もっといい書き方などがあれば教えて頂けると嬉しいです。

動作環境

macOS 10.15.4において
Version 1.0.5
Version 1.1.1
Version 1.2.0
Version 1.3.1
Version 1.4.0
で以下のコードが動作することを確認済みです。

出力が異なったものはコメントでv1.x.yと表記しました。

配列を作成する

1次元配列

各要素は,で区切る。1次元配列は列ベクトルであることに注意。

julia> [1]
1-element Array{Int64,1}:
 1

julia> [1, 3, 4]
3-element Array{Int64,1}:
 1
 3
 4

julia> Float32[1, 3, 4]  # type指定は前に
3-element Array{Float32,1}:
 1.0
 3.0
 4.0

連番や等差数列

Base.collect

julia> Vector(1:5)  # start:end
5-element Array{Int64,1}:
 1
 2
 3
 4
 5

julia> Vector(1:2:5)  # start:step:end
3-element Array{Int64,1}:
 1
 3
 5

julia> Array(1:2:5)
3-element Array{Int64,1}:
 1
 3
 5

julia> [1:2:5;]
3-element Array{Int64,1}:
 1
 3
 5

julia> collect(1:2:5)
3-element Array{Int64,1}:
 1
 3
 5

julia> [i for i in 1:2:5]  # 内包表記
3-element Array{Int64,1}:
 1
 3
 5

start:end:stepではなくstart:step:endとすることに注意。

2次元配列

各要素は空白で区切る。行を追加するなら;または改行を使う。

julia> [1 3 4]
1×3 Array{Int64,2}:
 1  3  4

julia> [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> [1 2
        3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> [1 2;  # ;と改行を合わせても大丈夫
        3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> [1; 3; 5]  # 各行の要素が一つなら1次元配列になる
3-element Array{Int64,1}:
 1
 3
 5

単位行列

Iを使うためにusing LinearAlgebraをする。

julia> using LinearAlgebra

julia> Matrix(1.0I, 3, 3)
3×3 Array{Float64,2}:
 1.0  0.0  0.0
 0.0  1.0  0.0
 0.0  0.0  1.0

julia> Matrix{Int32}(1I, (3, 3))  # tupleでもok
3×3 Array{Int32,2}:
 1  0  0
 0  1  0
 0  0  1

julia> Array(1I, (3, 3))  # Arrayでも
3×3 Array{Int64,2}:
 1  0  0
 0  1  0
 0  0  1

julia> collect(1I(3))  # v1.2.0以降
3×3 Array{Int64,2}:
 1  0  0
 0  1  0
 0  0  1

Base.oneやBase.oneunitに正方行列を渡す。

julia> a = rand(3, 3); one(a)
3×3 Array{Float64,2}:
 1.0  0.0  0.0
 0.0  1.0  0.0
 0.0  0.0  1.0

julia> b = rand(Int32, 2, 2); oneunit(b)
2×2 Array{Int32,2}:
 1  0
 0  1

julia/array.jl at master · JuliaLang/Julia - Github

ベクトルから行列に

julia> a = Vector(1:3)
3-element Array{Int64,1}:
 1
 2
 3

julia> a[:, :]  # 軸追加
3×1 Array{Int64,2}:
 1
 2
 3

julia> b = Vector(4:6); [a b]  # 結合
3×2 Array{Int64,2}:
 1  4
 2  5
 3  6

n次元配列

全要素0の配列

Base.zeros
引数は配列の各次元。

julia> zeros(1)
1-element Array{Float64,1}:
 0.0

julia> zeros(2, 2)
2×2 Array{Float64,2}:
 0.0  0.0
 0.0  0.0

julia> zeros((2, 2))  # tupleでもok
2×2 Array{Float64,2}:
 0.0  0.0
 0.0  0.0

julia> zeros(Int32, (3, 2, 1))  # type指定は一番最初の引数に
3×2×1 Array{Int32,3}:
[:, :, 1] =
 0  0
 0  0
 0  0

Base.zero

julia> a = rand(2, 2)
2×2 Array{Float64,2}:
 0.787291  0.299069
 0.647972  0.561586

julia> zero(a)  # 引数と同じ形状の全要素0の配列を作れる
2×2 Array{Float64,2}:
 0.0  0.0
 0.0  0.0

全要素1の配列

Base.ones
使い方はzerosと同じ。

julia> ones(Int8, (3, 2, 1))
3×2×1 Array{Int8,3}:
[:, :, 1] =
 1  1
 1  1
 1  1

任意の値で初期化した配列

Base.fill
最初の引数は初期化する値、そのあとは生成する配列の形状。

julia> fill(3, 2, 2)
2×2 Array{Int64,2}:
 3  3
 3  3

julia> fill(5.0, (2, 2, 1))  # tupleでもok
2×2×1 Array{Float64,3}:
[:, :, 1] =
 5.0  5.0
 5.0  5.0

未初期化の配列

julia> Vector{Int32}(undef, 3)  # 1次元配列
3-element Array{Int32,1}:
 779479344
     32525
 725270768

julia> Matrix{Float64}(undef, 2, 3)  # 2次元配列
2×3 Array{Float64,2}:
 6.90183e-310  6.90183e-310  6.90183e-310
 6.90183e-310  6.90183e-310  6.90183e-310

julia> Array{Float64}(undef, 2, 3)  # n次元配列
2×3 Array{Float64,2}:
 6.90183e-310  6.90183e-310  6.90183e-310
 6.90183e-310  6.90183e-310  6.90183e-310

julia> Array{Float32}(undef, (3, 3, 1))  # tupleでもok
3×3×1 Array{Float32,3}:
[:, :, 1] =
 1.68211e-11  4.55772e-41  1.68216e-11
 4.55772e-41  1.68214e-11  4.55772e-41
 1.68213e-11  4.55772e-41  8.0396e-13 

乱数

一様分布に従う乱数

Base.rand

julia> rand(2)  # 0~1の一様分布
2-element Array{Float64,1}:
 0.9730703223244999
 0.6378299748997536

julia> rand(Int32, 3, 1)  # type指定は一番最初の引数に
3×1 Array{Int32,2}:
    42502547
 -1786881158
  1936441579

julia> rand(Float16, (3, 3))  # tupleでもok
3×3 Array{Float16,2}:
 0.701   0.9404  0.8955
 0.2568  0.2178  0.376
 0.3643  0.9795  0.6006

要素がBoolの乱数

Random.bitrand
要素数が大きい時はbitrandを使った方が高速。コメント欄を参考にして下さい。

julia> using Random

julia> bitrand((2, 2))  # tupleでもok
2×2 BitArray{2}:  # v1.0.5, 1.1.1
  true  false
 false  false

2×2 BitArray{2}:  # v1.2.0, v1.3.1
 1  0
 0  0

標準正規分布に従う乱数

Base.randn

julia> randn(Float32, (2, 2))  # tupleでもok
2×2 Array{Float32,2}:
 -0.0751658  -1.95547 
  1.51167    -0.790138

配列の要素にアクセスする

1次元配列

一つの要素を取り出す

基本はa[index]で指定する(Linear indexing)。indexは0ではなく1から開始することに注意。

julia> a = Vector(1:3)
3-element Array{Int64,1}:
 1
 2
 3

julia> a[1]  # Linear indexing
1

julia> a[begin]  # v1.4.0以降
1

julia> a[3]
3

julia> a[end]
3

julia> a[CartesianIndex(end)]
3

julia> a[2, 1, 1, 1]  # これでも大丈夫
2

julia> a[CartesianIndex(2, 1, 1, 1)]
2

最後の要素のindexは-1ではなくendを使う。

複数の要素を取り出す

スライスが使える。

julia> a = Vector(1:5)
5-element Array{Int64,1}:
 1
 2
 3
 4
 5

julia> a[1:end]
5-element Array{Int64,1}:
 1
 2
 3
 4
 5

julia> a[begin:end]  # v1.4.0以降
5-element Array{Int64,1}:
 1
 2
 3
 4
 5

julia> a[2:end-1]
3-element Array{Int64,1}:
 2
 3
 4

julia> a[1:2:end]
3-element Array{Int64,1}:
 1
 3
 5

startやendは片方だけでスライスできない。

julia> a = Vector(1:5); a[:3]  # startを指定しないとendの要素のみ
3

julia> a[2:]  # endを指定しないとError
ERROR: syntax: missing last argument in "2:" range expression

各要素がindexの配列でも可能。

julia> a = Vector(1:5); a[[1, 2, 5]]
3-element Array{Int64,1}:
 1
 2
 5

julia> a[[3, 5, 3]]
3-element Array{Int64,1}:
 3
 5
 3

julia> a[[CartesianIndex(3), CartesianIndex(end), CartesianIndex(3)]]
3-element Array{Int64,1}:
 3
 5
 3

2次元配列

1つの要素を取り出す

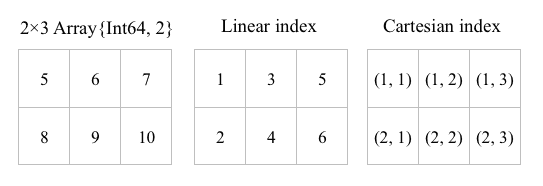
a[index]で指定するときは左の列から順番にindexがついていることに注意。
またはa[縦方向のindex, 横方向のindex]で指定する。
Linear indexは配列を1列に並べたときのindex。
Cartesian indexは配列の次元ごとのindex。

julia> a = [5 6 7; 8 9 10]
2×3 Array{Int64,2}:
 5  6   7
 8  9  10

julia> a[1]  # Linear indexing
5

julia> a[begin]  # v1.4.0以降
5

julia> a[1, 1]  # Cartesian indexing
5

julia> a[begin, begin] # v1.4.0以降
5

julia> a[end]  # Linear indexing
10

julia> a[1, 3]  # Cartesian indexing
7

julia> a[end, end]  # Cartesian indexing
10

endは配列の各次元の最後のindexを指す。そのためa[end]はa[6]、a[end, end]はa[2, 3]と同じ。

複数の要素を取り出す

スライス、またはlinear index(cartesian index)を要素にもつ配列が使える

行や列を1次元配列で

1つの列、特に1つの行を取り出すときに1次元配列なることに注意

julia> a = reshape(1:9, (3, 3))
3×3 reshape(::UnitRange{Int64}, 3, 3) with eltype Int64:
 1  4  7
 2  5  8
 3  6  9

julia> a[:, 1]  # 1列目
3-element Array{Int64,1}:
 1
 2
 3

julia> a[2, :]  # 2行目
3-element Array{Int64,1}:
 2
 5
 8

julia> a[[2, 5, 8]]  # Linear indexを要素にもつ配列でも可能
3-element Array{Int64,1}:
 2
 5
 8

# CartesianIndexを要素にもつ配列でも可能
julia> a[[CartesianIndex(2, 1), CartesianIndex(2, 2), CartesianIndex(2, 3)]]
3-element Array{Int64,1}:
 2
 5
 8

julia> a[CartesianIndex.(2, 1:3)]  # ブロードキャスト
3-element Array{Int64,1}:
 2
 5
 8

行や列を2次元配列で

julia> a = reshape(1:9, (3, 3))
3×3 reshape(::UnitRange{Int64}, 3, 3) with eltype Int64:
 1  4  7
 2  5  8
 3  6  9

julia> a[:, 2:end]  # 複数列
3×2 Array{Int64,2}:
 4  7
 5  8
 6  9

julia> a[:, 1:1]  # 1つの列を2次元配列で取り出したい時
3×1 Array{Int64,2}:
 1
 2
 3

julia> a[1:2, :]  # 複数行
2×3 Array{Int64,2}:
 1  4  7
 2  5  8

julia> a[2:2, :]  # 1つの行を2次元配列で取り出したい時
1×3 Array{Int64,2}:
 2  5  8

正方行列の対角成分のみ

LinearAlgebra.diag
CartesianIndexとブロードキャスト.を使うか、diagを使う。

julia> a = [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> a[CartesianIndex.(1:2, 1:2)]  # 対角成分
2-element Array{Int64,1}:
 1
 4

julia> a[CartesianIndex.(1:2, 2:-1:1)]  # 反対角成分
2-element Array{Int64,1}:
 2
 3

julia> using LinearAlgebra

julia> diag(a)  # 対角成分
2-element Array{Int64,1}:
 1
 4

n次元配列

条件を満たす部分を取り出す

trueとfalseを要素にもつ配列を使って取り出せる(Logical indexing)。
条件式にはブロードキャスト.を使うこと。

julia> a = reshape(1:9, (3, 3))
3×3 reshape(::UnitRange{Int64}, 3, 3) with eltype Int64:
 1  4  7
 2  5  8
 3  6  9

julia> a[a .< 5]
4-element Array{Int64,1}:
 1
 2
 3
 4

julia> a[a .> 5]
4-element Array{Int64,1}:
 6
 7
 8
 9

julia> a[a .== 5]
1-element Array{Int64,1}:
 5

julia> a[3 .< a .<= 7]
4-element Array{Int64,1}:
 4
 5
 6
 7

フィルターを使って偶奇

Base.filter
filiterは最初の引数に関数を渡す。

julia> a = reshape(1:9, (3, 3))
3×3 reshape(::UnitRange{Int64}, 3, 3) with eltype Int64:
 1  4  7
 2  5  8
 3  6  9

julia> filter(isodd, a)  # 奇数
5-element Array{Int64,1}:
 1
 3
 5
 7
 9

julia> filter(iseven, a)  # 偶数
4-element Array{Int64,1}:
 2
 4
 6
 8

配列の要素に代入する

複数の要素への代入はブロードキャスト.を使用する。

1次元配列

julia> a = Vector(1:4)
4-element Array{Int64,1}:
 1
 2
 3
 4

julia> a[2] = 0; a
4-element Array{Int64,1}:
 1
 0
 3
 4

julia> a[a .< 4] .= 0; a
4-element Array{Int64,1}:
 0
 0
 0
 4

julia> b = a; b[end] = 0; a  # 参照先の値も変わる
4-element Array{Int64,1}:
 0
 0
 0
 0

2次元配列

julia> a = [1 2 3; 4 5 6]
2×3 Array{Int64,2}:
 1  2  3
 4  5  6

julia> a[1, :] .= 0; a  # 1行に代入
2×3 Array{Int64,2}:
 0  0  0
 4  5  6

julia> a[:, 2:end] .= 2; a  # 複数列に代入
2×3 Array{Int64,2}:
 0  2  2
 4  2  2

julia> a[a .== 2] .= 3; a
2×3 Array{Int64,2}:
 0  3  3
 4  3  3

julia> a .= 1
2×3 Array{Int64,2}:
 1  1  1
 1  1  1

RangeをreshapeしたあとはArrayに変換してから代入することに注意。

julia> a = reshape(1:6, (2, 3))
2×3 reshape(::UnitRange{Int64}, 2, 3) with eltype Int64:
 1  3  5
 2  4  6

julia> a[1, 1] = 0  # Arrayではないので代入できない
ERROR: indexed assignment fails for a reshaped range; consider calling collect

julia> a = Array(a)  # Arrayに変換
2×3 Array{Int64,2}:
 1  3  5
 2  4  6

julia> a[1, 1] = 0; a  # Arrayなので代入できる
2×3 Array{Int64,2}:
 0  3  5
 2  4  6

配列の情報を取得する

次元数を取得する

Base.ndims

julia> a = ones(2, 3, 4); ndims(a)  # 3次元配列
3

形状を取得する

Base.size

julia> a = ones(2, 3, 4); size(a)
(2, 3, 4)

julia> size(a, 2)  # 取得したい次元が1つだけなら
3

全要素数を取得する

Base.length

julia> a = [1, 2, 3]; length(a)
3
julia> b = [1 2; 3 4]; length(b)
4

型を取得する

Base.eltype, Core.typeof

julia> a = ones(2, 3)
2×3 Array{Float64,2}:
 1.0  1.0  1.0
 1.0  1.0  1.0

julia> eltype(a) # 要素の型
Float64

julia> typeof(a)  # 配列の型
Array{Float64,2}

配列の形状や次元数の操作をする

形状を変える

Base.reshape
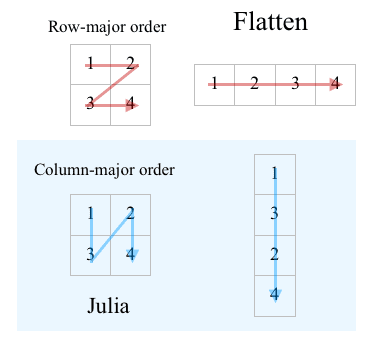
Juliaはcolumn-major orderなのでreshape後の順番に注意。Row- and column-major order - Wikipedia

julia> a = Vector(1:4)
4-element Array{Int64,1}:
 1
 2
 3
 4

julia> reshape(a, 2, 2)
2×2 Array{Int64,2}:
 1  3
 2  4

julia> reshape(1:4, (2, 2, 1))  # tupleでもok
2×2×1 reshape(::UnitRange{Int64}, 2, 2, 1) with eltype Int64:
[:, :, 1] =
 1  3
 2  4

軸を入れ替える

1次元配列と2次元配列(転置)

Base.transpose

julia> a = Vector(1:3)
3-element Array{Int64,1}:
 1
 2
 3

julia> transpose(a)  # 行ベクトル
1×3 LinearAlgebra.Transpose{Int64,Array{Int64,1}}:
 1  2  3

julia> a'  #　transpose(a)と同じ
1×3 LinearAlgebra.Adjoint{Int64,Array{Int64,1}}:
 1  2  3

julia> b = [1 2; 3 4; 5 6]
3×2 Array{Int64,2}:
 1  2
 3  4
 5  6

julia> transpose(b)
2×3 LinearAlgebra.Transpose{Int64,Array{Int64,2}}:
 1  3  5
 2  4  6

julia> b'
2×3 LinearAlgebra.Adjoint{Int64,Array{Int64,2}}:
 1  3  5
 2  4  6

n次元配列

Base.permutedims

julia> a = [1 2 3; 4 5 6]
2×3 Array{Int64,2}:
 1  2  3
 4  5  6

julia> permutedims(a)  # permutedims(a, (2, 1))と同じ
3×2 Array{Int64,2}:
 1  4
 2  5
 3  6

julia> b = ones(4, 5, 6); size(permutedims(b, (2, 1, 3)))  # 入れ替える軸の順番はtupleとか配列だけ
(5, 4, 6)

軸を追加する

後ろのみ

julia> a = [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> a[:, :, :]
2×2×1 Array{Int64,3}:
[:, :, 1] =
 1  2
 3  4

julia> a[:, :, :, :]
2×2×1×1 Array{Int64,4}:
[:, :, 1, 1] =
 1  2
 3  4

任意の位置

julia> a = [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> const newaxis = [CartesianIndex()]  # numpyっぽく
1-element Array{CartesianIndex{0},1}:
 CartesianIndex()

julia> a[:, newaxis, newaxis, :]
2×1×1×2 Array{Int64,4}:
[:, :, 1, 1] =
 1
 3

[:, :, 1, 2] =
 2
 4

Julia Users - equivalent of numpy newaxis?

軸を削除する

Base.dropdims
dimsで指定した1次元の軸を削除できる。

julia> a = reshape(1:4, (2, 1, 2, 1))
2×1×2×1 reshape(::UnitRange{Int64}, 2, 1, 2, 1) with eltype Int64:
[:, :, 1, 1] =
 1
 2

[:, :, 2, 1] =
 3
 4

julia> dropdims(a, dims=2)
2×2×1 reshape(::UnitRange{Int64}, 2, 2, 1) with eltype Int64:
[:, :, 1] =
 1  3
 2  4

julia> size(dropdims(a, dims=(2, 4)))  # 複数落とす
(2, 2)

n次元配列を1次元配列にする

Base.vec
Column-major orderなので、順番に注意。

julia> a = [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> vec(a)
4-element Array{Int64,1}:
 1
 3
 2
 4

julia> a[:]
4-element Array{Int64,1}:
 1
 3
 2
 4

Access arrays in memory order, along columns - The Julia Language

配列の型を変換する

Base.convert

julia> a = [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> Array{Float32}(a)
2×2 Array{Float32,2}:
 1.0  2.0
 3.0  4.0

julia> b = Vector(1:3)
3-element Array{Int64,1}:
 1
 2
 3

julia> Array{Float16}(b)  # Vector{Float16}(b)でも可
3-element Array{Float16,1}:
 1.0
 2.0
 3.0

julia> convert(Array{Float16}, b)
3-element Array{Float16,1}:
 1.0
 2.0
 3.0

配列同士を結合する

縦に結合する

Base.cat, Base.vcat
catを使うときはdims=1にする。[ ; ]を使ってもいい。

julia> a = ([0, 1, 2], [3, 4]); vcat(a...)  # 列ベクトル同士
5-element Array{Int64,1}:
 0
 1
 2
 3
 4

julia> b = [0 1 2; 3 4 5]
2×3 Array{Int64,2}:
 0  1  2
 3  4  5

julia> c = [6, 7, 8]'
1×3 LinearAlgebra.Adjoint{Int64,Array{Int64,1}}:
 6  7  8

julia>  vcat(b, c)  # 行列と行ベクトルの結合
3×3 Array{Int64,2}:
 0  1  2
 3  4  5
 6  7  8

julia> vcat(b, b)  # 行列同士
4×3 Array{Int64,2}:
 0  1  2
 3  4  5
 0  1  2
 3  4  5

julia> cat(b, b, dims=1)
4×3 Array{Int64,2}:
 0  1  2
 3  4  5
 0  1  2
 3  4  5

julia> [b; b]
4×3 Array{Int64,2}:
 0  1  2
 3  4  5
 0  1  2
 3  4  5

横に結合する

Base.cat, Base.hcat
catを使うときはdims=2にする。[ ]を使ってもいい。

julia> a = ([0 1 2], [3 4 5]); hcat(a...)
1×6 Array{Int64,2}:
 0  1  2  3  4  5

julia> b = ([0, 1, 2], [3, 4, 5]); hcat(b...)  # 列ベクトル同士
3×2 Array{Int64,2}:
 0  3
 1  4
 2  5

julia> c = [0 1; 2 3; 4 5]
3×2 Array{Int64,2}:
 0  1
 2  3
 4  5

julia> d = [6, 7, 8]
3-element Array{Int64,1}:
 6
 7
 8

julia> hcat(c, d)  # 行列と列ベクトルの結合
3×3 Array{Int64,2}:
 0  1  6
 2  3  7
 4  5  8

julia> hcat(c, c)  # 行列同士
3×4 Array{Int64,2}:
 0  1  0  1
 2  3  2  3
 4  5  4  5

julia> cat(c, c, dims=2)
3×4 Array{Int64,2}:
 0  1  0  1
 2  3  2  3
 4  5  4  5

julia> [c c]
3×4 Array{Int64,2}:
 0  1  0  1
 2  3  2  3
 4  5  4  5

その他

ソートする

Base.sort

julia> a = [3, 1, 4, 2]
4-element Array{Int64,1}:
 3
 1
 4
 2

julia> sort(a)  # 昇順
4-element Array{Int64,1}:
 1
 2
 3
 4

julia> sort(a, rev=true)  # 降順
4-element Array{Int64,1}:
 4
 3
 2
 1

2次元以上はdimsでソートする方向を指定する

julia> a = [3 1 4 2]
1×4 Array{Int64,2}:
 3  1  4  2

julia> sort(a, dims=2)
1×4 Array{Int64,2}:
 1  2  3  4

逆順にする

Base.reverse

julia> a = Vector(0:2)
3-element Array{Int64,1}:
 0
 1
 2

julia> reverse(a)
3-element Array{Int64,1}:
 2
 1
 0

julia> a[end:-1:1]  # スライスでも可能
3-element Array{Int64,1}:
 2
 1
 0

引数を追加することで逆順にする範囲を指定できる

julia> a = Vector(1:5)
5-element Array{Int64,1}:
 1
 2
 3
 4
 5

julia> reverse(a, 3)  # index3から最後まで逆順
5-element Array{Int64,1}:
 1
 2
 5
 4
 3

julia> reverse(a, 2, 4)  # index2から4まで逆順
5-element Array{Int64,1}:
 1
 4
 3
 2
 5

dimsで軸を指定できる。

julia> a = [0 1 2; 3 4 5]
2×3 Array{Int64,2}:
 0  1  2
 3  4  5

julia> reverse(a, dims=2)  # 横方向で逆順
2×3 Array{Int64,2}:
 2  1  0
 5  4  3

julia> a[:, end:-1:1]  # スライスでも
2×3 Array{Int64,2}:
 2  1  0
 5  4  3

繰り返す

Base.repeat

要素ごとに繰り返す

配列の後の引数が1つなら縦方向に、引数が2つなら縦方向と横方向に繰り返す。横方向のみに繰り返したいなら, 縦方向を1にすればよい。

julia> repeat([0], 3)  # 縦方向に
3-element Array{Int64,1}:
 0
 0
 0

julia> repeat([0], 1, 3)  # 横方向に
1×3 Array{Int64,2}:
 0  0  0

julia> repeat([0], 1, 3, 1)
1×3×1 Array{Int64,3}:
[:, :, 1] =
 0  0  0

要素が複数あるときはinnerを使うといい

julia> repeat([1 2 3], inner=(1, 2))
1×6 Array{Int64,2}:
 1  1  2  2  3  3

julia> a = [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> repeat(a, inner=(1, 3, 1))
2×6×1 Array{Int64,3}:
[:, :, 1] =
 1  1  1  2  2  2
 3  3  3  4  4  4 

タイル状に並べる

julia> a = Vector(1:2)
2-element Array{Int64,1}:
 1
 2

julia> repeat(a, 2)  # 縦方向に
4-element Array{Int64,1}:
 1
 2
 1
 2

julia> repeat(a, 1, 2)  # 横方向に
2×2 Array{Int64,2}:
 1  1
 2  2

julia> b = [0 1 2]
1×3 Array{Int64,2}:
 0  1  2

julia> repeat(b, 3)  # 縦方向に
3×3 Array{Int64,2}:
 0  1  2
 0  1  2
 0  1  2

julia> repeat(b, 1, 3)  # 横方向に
1×9 Array{Int64,2}:
 0  1  2  0  1  2  0  1  2

julia> repeat(b, 1, 3, 1)
1×9×1 Array{Int64,3}:
[:, :, 1] =
 0  1  2  0  1  2  0  1  2

outerを使う場合はinnerと合わせて使うことができる

julia> a = [1 2 3]
1×3 Array{Int64,2}:
 1  2  3

julia> repeat(a, outer=(2, 2, 1))  # outerだけ
2×6×1 Array{Int64,3}:
[:, :, 1] =
 1  2  3  1  2  3
 1  2  3  1  2  3

julia> repeat(a, inner=(1, 1, 2), outer=(2, 2))  # innerと組み合わせる
2×6×2 Array{Int64,3}:
[:, :, 1] =
 1  2  3  1  2  3
 1  2  3  1  2  3

[:, :, 2] =
 1  2  3  1  2  3
 1  2  3  1  2  3

julia> repeat(a, inner=(1, 1, 2))  # innerだけだと
1×3×2 Array{Int64,3}:
[:, :, 1] =
 1  2  3

[:, :, 2] =
 1  2  3

回転させる

90度

Base.rotl90, Base.rotr90

julia> a = [0 1; 3 4]
2×2 Array{Int64,2}:
 0  1
 3  4

julia> rotl90(a)  # 左に90度
2×2 Array{Int64,2}:
 1  4
 0  3

julia> rotl90(a, 2)  # 左に180度
2×2 Array{Int64,2}:
 4  3
 1  0

julia> rotr90(a)  # 右に90度
2×2 Array{Int64,2}:
 3  0
 4  1

julia> rotr90(a, 2)  # 右に180度
2×2 Array{Int64,2}:
 4  3
 1  0

180度

Base.rot180

julia> a = [0 1; 3 4]
2×2 Array{Int64,2}:
 0  1
 3  4

julia> rot180(a)
2×2 Array{Int64,2}:
 4  3
 1  0

julia> rot180(a, 2)  # 元の位置に戻る
2×2 Array{Int64,2}:
 0  1
 3  4

シフトさせる

Base.circshift

julia> circshift(1:5, 2)
5-element Array{Int64,1}:
 4
 5
 1
 2
 3

julia> a = reshape(1:9, (3, 3))
3×3 reshape(::UnitRange{Int64}, 3, 3) with eltype Int64:
 1  4  7
 2  5  8
 3  6  9

julia> circshift(a, -1)  # 上にシフト
3×3 Array{Int64,2}:
 2  5  8
 3  6  9
 1  4  7

julia> circshift(a, 1)  # 下にシフト
3×3 Array{Int64,2}:
 3  6  9
 1  4  7
 2  5  8

julia> circshift(a, (0, -1))  # 左にシフト
3×3 Array{Int64,2}:
 4  7  1
 5  8  2
 6  9  3

julia> circshift(a, (0, 1))  # 右にシフト
3×3 Array{Int64,2}:
 7  1  4
 8  2  5
 9  3  6

最大値(最小値)を取得する

Base.maximum, Base.minimum, Base.extrema

julia> a = reshape(1:6, (2, 3))
2×3 reshape(::UnitRange{Int64}, 2, 3) with eltype Int64:
 1  3  5
 2  4  6

julia> maximum(a)  # 最大値
6

julia> minimum(a)  # 最小値
1

julia> extrema(a)  # 最小値と最大値の両方
(1, 6)

dimsで取得したい最大値(最小値)の方向を指定する

julia> a = reshape(1:6, (2, 3))
2×3 reshape(::UnitRange{Int64}, 2, 3) with eltype Int64:
 1  3  5
 2  4  6

julia> maximum(a, dims=1)  # 縦方向に
1×3 Array{Int64,2}:
 2  4  6

julia> maximum(a, dims=2)  # 横方向に
2×1 Array{Int64,2}:
 5
 6

julia> maximum(a, dims=(1, 2))  # dimsにtupleもok
1×1 Array{Int64,2}:
 6

julia> extrema(a, dims=2)
2×1 Array{Tuple{Int64,Int64},2}:
 (1, 5)
 (2, 6)

インデックスを取得する

Base.argmax, Base.argmin

julia> argmax([1, 2, 3, 4])
4

julia> a = [1 4; 4 3]
2×2 Array{Int64,2}:
 1  4
 4  3

julia> argmax(a)  # 最初の最大値のindex
CartesianIndex(2, 1)

julia> a[CartesianIndex(2, 1)]  # 最大値を取得できる
4

dimsで取得したいインデックスの方向を指定する

julia> a = [1 4; 4 3]
2×2 Array{Int64,2}:
 1  4
 4  3

julia> argmax(a, dims=1)  # 縦方向に
1×2 Array{CartesianIndex{2},2}:
 CartesianIndex(2, 1)  CartesianIndex(1, 2)

julia> argmax(a, dims=2)  # 横方向に
2×1 Array{CartesianIndex{2},2}:
 CartesianIndex(1, 2)
 CartesianIndex(2, 1)

julia> argmax(a, dims=(1, 2))
1×1 Array{CartesianIndex{2},2}:
 CartesianIndex(2, 1)

最小値ならargmaxをargminに変えればいい。

最大値(最小値)とインデックスを取得する

Base.findmax, Base.findmin

julia> a = [1 4; 3 4]
2×2 Array{Int64,2}:
 1  4
 3  4

julia> findmax(a)  # 最初の最大値とindex
(4, CartesianIndex(1, 2))

dimsで取得したい最大値(最小値)とインデックスの方向を指定する。

julia> a = [1 4; 3 4]
2×2 Array{Int64,2}:
 1  4
 3  4

julia> findmax(a, dims=1)  # 縦方向に
([3 4], CartesianIndex{2}[CartesianIndex(2, 1) CartesianIndex(1, 2)])

julia> findmax(a, dims=2)  # 横方向に
([4; 4], CartesianIndex{2}[CartesianIndex(1, 2); CartesianIndex(2, 2)])

julia> findmax(a, dims=(1, 2))
([4], CartesianIndex{2}[CartesianIndex(1, 2)])

最小値ならfindmaxをfindminに変えればいい。

シャッフルする

Random.shuffle
using Randomを使う

julia> using Random

julia> shuffle(1:3)
3-element Array{Int64,1}:
 3
 2
 1

julia> a = [1 2; 3 4]
2×2 Array{Int64,2}:
 1  2
 3  4

julia> a[shuffle(1:end), :]  # 縦方向に
2×2 Array{Int64,2}:
 3  4
 1  2

julia> a[:, shuffle(1:end)]  # 横方向に
2×2 Array{Int64,2}:
 2  1
 4  3

julia> shuffle(a)  # 次元を保ったまま全体で
2×2 Array{Int64,2}:
 4  3
 2  1

二つの配列の対応関係を保ったままシャッフルする

julia> using Random

julia> a = Vector(6:10); b = Vector(11:15); idx = shuffle(1:5)
5-element Array{Int64,1}:
 3
 2
 4
 5
 1

julia> a[idx]
5-element Array{Int64,1}:
  8
  7
  9
 10
  6

julia> b[idx]
5-element Array{Int64,1}:
 13
 12
 14
 15
 11

コピーする

Base.copy, Base.deepcopy

julia> a = [1 2 3; 4 5 6]
2×3 Array{Int64,2}:
 1  2  3
 4  5  6

julia> b = copy(a)
2×3 Array{Int64,2}:
 1  2  3
 4  5  6

julia> a[2, 2] = 0; a
2×3 Array{Int64,2}:
 1  2  3
 4  0  6

julia> b  # 変化なし
2×3 Array{Int64,2}:
 1  2  3
 4  5  6

deepcopyは配列の配列などを扱う時に役立つ。

julia> a = [[1, 2, 3], [4, 5, 6]]
2-element Array{Array{Int64,1},1}:
 [1, 2, 3]
 [4, 5, 6]

julia> b = copy(a)
2-element Array{Array{Int64,1},1}:
 [1, 2, 3]
 [4, 5, 6]

julia> c = deepcopy(a)
2-element Array{Array{Int64,1},1}:
 [1, 2, 3]
 [4, 5, 6]

julia> a[1][2] = 0; a
2-element Array{Array{Int64,1},1}:
 [1, 0, 3]
 [4, 5, 6]

julia> b
2-element Array{Array{Int64,1},1}:
 [1, 0, 3]
 [4, 5, 6]

julia> c  # 変化なし
2-element Array{Array{Int64,1},1}:
 [1, 2, 3]
 [4, 5, 6]

What is the difference between copy() and deepcopy()? - Usage - JuliaLang

参考文献

The Julia Language v1.4.0
MATLAB–Python–Julia cheatsheet — Cheatsheets by QuantEcon documentation
ベクトルや行列の作り方.ipynb