対象
- AIに興味がある人
- 興味があるけど何からすれば良いか分からない人
- AIで何ができるのか知りたい人
前提
- Googleアカウントを持っている
- Google Driveの基本的な使い方を知っている
- Python3の基本的な使い方を知っている
- 機械学習の理論については扱わない
機械学習の概要に関しては以下を参照
ゴール
- テーブルデータの目的の列の値をある程度の精度で予測できる
- データ分析に必要な専門用語が少し分かる
- データをグラフで表示できる
前知識
予測するデータの種類によって使うモデルが変わる
-
分類
0か1の2種類のラベルを予測すること
例)ウイルス検査の陽性・陰性、ある顧客がサービスを解約するか否か -
回帰
数値を予測すること
例)売上、来客数
今回扱うのは回帰である
流れ
- Google Colaboratoryの準備
- 初期画面
- ランタイムの接続
- 画面の説明
- セルの追加
- データの読み込み
- データの確認
- 先頭表示(head)
- カラムの説明
- 詳細情報の確認(describe)
- 各カラムの欠損値と型確認(info)
- ヒストグラム(hist)
- 相関の確認(scatter_matrix)
- 場所ごとの住宅価格の中央値を確認(Basemap)
- ここまでで分かったこと - part1
- モデルの学習と予測 - part1
- データを学習用・検証用・テスト用に分割
- 何故検証用データを用意するのか?
- 予測結果の精度を描画する関数を定義
- 線形回帰の学習と予測精度の可視化(前処理なし)
- XGBoostの学習と予測精度の可視化(前処理なし)
- ランダムフォレストの学習と予想精度の可視化(前処理なし)
- ここまでで分かったこと - part2
- 前処理
- 外れ値の確認
- 外れ値の削除
- all_dataをtrainとtestに分割
- モデルの学習と予測 - part2
- データを学習用・検証用・テスト用に分割
- 標準化
- 線形回帰の学習と予測精度の可視化(前処理あり)
-
- XGBoostの学習と予測精度の可視化(前処理あり)
- ランダムフォレストの学習と予想精度の可視化(前処理あり)
- まとめ
- その他参考文献
Google Colaboratoryの準備
- Google Driveにアクセス
- 作業用にフォルダを作成(今回はhandsonという名前のフォルダを作成)
- 作成したフォルダに移動
- 「右クリック」 => 「その他」 => 「Google Colaboratory」を選択
初期画面
ランタイムの接続
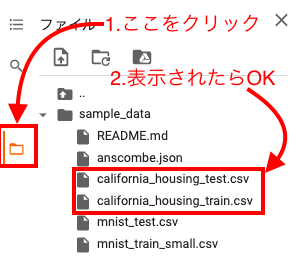
左側のタブからsample_dataを開いて、california_housing_{train/test}.csvがあることを確認できたらOK
画面の説明
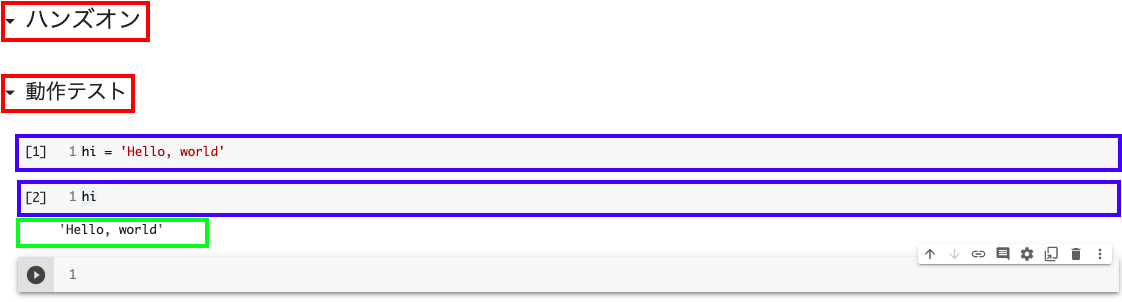
赤枠:テキストセル(マークダウン記法)
青枠:コードセル(python)
緑枠:出力結果
セルの実行はセルを選択した状態で「Shift」+「Enter」かセル左側のスタートアイコンで実行できる
実行はセルごとに行われ、変数の値はセルを移動しても保持される
コードセルの実行した順番は青枠の左側の数字で分かる
コードセルの最後の変数が出力されるためprint(hi)を記述する必要がない(超便利!)
セルの追加
以下の画像左上の「+ コード」、「+ テキスト」やセル中央にカーソルを合わせると表示されるボタンで追加できる

詳細な使い方は以下を参照
ここからは適宜セルを追加して実行しよう
データの読み込み
今回はサンプルデータのcalifornia housingデータを使う
Colaboratoryにはあらかじめサンプルデータが用意されている
import pandas as pd
pd.options.display.precision = 3
train = pd.read_csv('sample_data/california_housing_train.csv')
test = pd.read_csv('sample_data/california_housing_test.csv')
pandasとは? - wiki
pandasは、プログラミング言語Pythonにおいて、データ解析を支援する機能を提供するライブラリである。特に、数表および時系列データを操作するためのデータ構造と演算を提供する
pd.options.display.precisionで小数点以下何桁を表示するか設定している(今回は説明の都合上、小数点以下3桁としている)
read_csvでcsvファイルを読み込むことができる
データの確認
ここからは、データを眺めてみます
先頭表示(head)
train.head()

headで先頭5行までのテーブルデータを確認できる(引数に値を入れるとその数まで表示される)
testも確認してみよう!
各カラムの説明
| カラム名 | 説明 |
|---|---|
| longitude | 経度 |
| latitude | 緯度 |
| housing_median_age | ブロックの築年数の中央値 |
| total_rooms | ブロック内の部屋の総数 |
| total_bedrooms | ブロック内の寝室の総数 |
| population | ブロック内に住む人の総数 |
| households | 1ブロックあたりの世帯数 |
| median_income | ブロック内の世帯収入の中央値 [万ドル] |
| median_house_value | ブロック内の住宅価格の中央値 [ドル] |
各カラムの詳細は以下
今回予測するカラムはmedian_house_valueでこれを目的変数と呼ぶ
それ以外のカラムは予測に必要なデータでこれを説明変数と呼ぶ
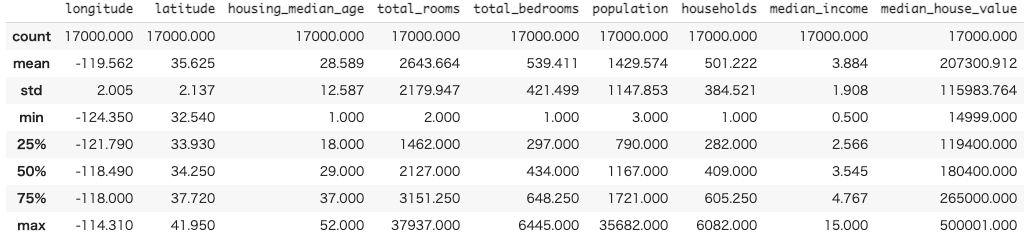
詳細情報の確認(describe)
train.describe()
describeで各列の以下の情報が表示される
| 名前 | 意味 |
|---|---|
| count | 行数 |
| mean | 平均値 |
| std | 標準偏差 |
| min | 最小値 |
| 25% | 第一四分位数 |
| 50% | 中央値 |
| 75% | 第三四分位数 |
| max | 最大値 |
testも確認してみよう!
各カラムの欠損値と型確認(info)
train.info()
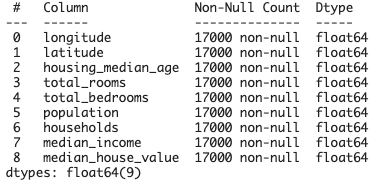
Non-Null Countの各項目の値がdescribeで確認したcountと同じ17000であるため、欠損値はないことが分かる
欠損値がある場合は、何かの値で補完したり、その行を削除して学習データに使わないなどの処理が必要となる
testも確認してみよう!
ヒストグラム(hist)
グラフ表示に必要なライブラリのインストール
import matplotlib.pyplot as plt
%matplotlib inline
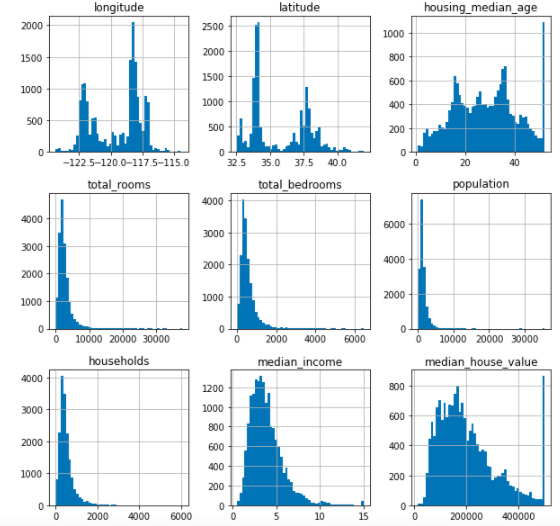
ヒストグラムの表示
train.hist(bins=50, figsize=(10, 10))
matplotlibとは? - wiki
Matplotlibは、プログラミング言語Pythonおよびその科学計算用ライブラリNumPyのためのグラフ描画ライブラリ
-
%matplotlib inlineはおまじないのようなもの -
histでヒストグラム表示 -
binsは棒の数 -
figsizeでグラフサイズ変更(お好みでどうぞ)
testも確認してみよう!
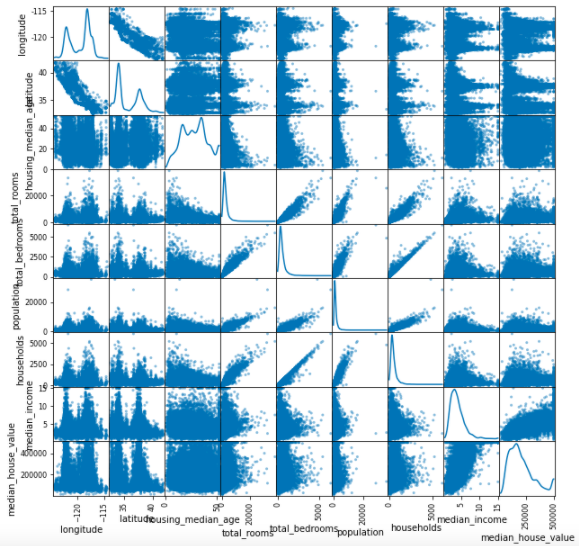
相関の確認(scatter_matrix)
pd.plotting.scatter_matrix(train, diagonal='kde', figsize=(10, 10))
参考文献
testも確認してみよう!
場所ごとの住宅価格の中央値を確認(Basemap)
Basemapのインストール
!apt-get install libgeos-3.5.0
!apt-get install libgeos-dev
!pip install https://github.com/matplotlib/basemap/archive/master.zip
以下が表示されたら、下のボタンからランタイムを再起動する

再起動したら、Basemapのインストールを含めて上から実行していく
Successfully built basemapが表示されたらOK
Basemapのインストールと地図上にプロットを表示する関数を定義
from mpl_toolkits.basemap import Basemap
def basemap(x, y, target):
fig = plt.figure(dpi=300)
xyrange = 0.5
m = Basemap(projection="cyl", resolution="i", llcrnrlat=y.min()-xyrange, urcrnrlat=y.max()+xyrange, llcrnrlon=x.min()-xyrange, urcrnrlon=x.max()+xyrange)
m.drawparallels(np.arange(-90, 90, 0.5), labels=[True, False, True, False],linewidth=0.0, fontsize=4)
m.drawmeridians(np.arange(0, 360, 0.5), labels=[True, False, False, True],linewidth=0.0, rotation=45, fontsize=4)
m.drawcoastlines(color='k')
m.arcgisimage(service='World_Street_Map', verbose=True, xpixels=1000, dpi=300)
plt.scatter(x, y, c=target, s=5, cmap=plt.get_cmap('jet'), alpha=0.4, linewidths=0)
plt.colorbar()
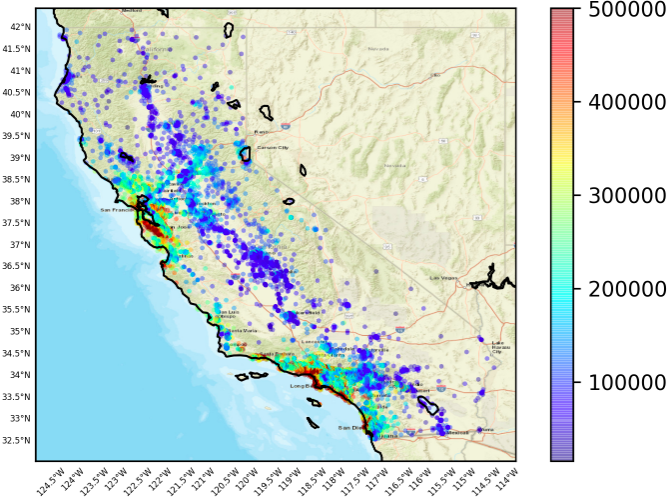
カリフォルニア周辺にデータをプロット
basemap(train['longitude'], train['latitude'], train['median_house_value'])
testも確認してみよう!
ここまでで分かったこと - part1
-
trainとtestのデータの分布がほとんど同じ(describeの各項目やヒストグラムがほとんど似てるため) -
housing_median_age、median_house_valueの最大値あたりが外れ値っぽい(ヒストグラムから) -
total_rooms、total_bedrooms、population、householdsがそれぞれ相関関係にありそう(相関のグラフより) - 海沿い物件の住宅価格の中央値は高そうだ(Basemapより)
外れ値とは? - wiki
外れ値(はずれち、英: outlier)は、統計学において、他の値から大きく外れた値のこと
これらを踏まえて、本来なら次に前処理を行う
しかし、前処理の重要性を理解するために、敢えて行わず機械学習モデルの学習に取り組む
モデルの学習と予測 - part1
前処理を行わず、学習を行なってみる
今回使うモデルは以下
- 線形回帰(線形モデル)
- XGBoost(決定木モデル)
- ランダムフォレスト(決定木モデル)
線形モデルの特徴
- 特徴量は数値
- 欠損値が扱えない
- 標準化が必要
- 単体では精度は高くなく、GBDTやニューラルネットに勝てることはほとんどない
決定木モデルの特徴
- 特徴量は数値
- 欠損値も扱える
- パラメータチューニングをしなくても精度が出やすい
- 不要な特徴量を追加しても精度が落ちにくい
- 特徴量をスケーリング(標準化や正規化)しなくて良い
ある程度の精度で予測したい場合は、決定木モデルの方が扱いやすくて簡単
今回は比較として、線形モデルも扱う
線形モデルには特徴量の標準化が必要だが、part1では、敢えて標準化を行わず、part2でどのくらい精度が変わるのか確認する
標準化とは? - データ科学便覧
統計学における標準化 (standardization) とは,与えられたデータを平均が0で分散が1のデータに変換する操作のことをいう.
データを学習用・検証用・テスト用に分割
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 目的変数
obj_var = 'median_house_value'
# テスト用の説明変数
x_test = test.drop(obj_var, axis=1)
# テスト用の目的変数
y_test = test[obj_var]
# 学習用の説明変数
x = train.drop(obj_var, axis=1)
# 学習用の目的変数
y = train[obj_var]
# 学習用データを、学習用と検証用に分割
x_train, x_valid, y_train, y_valid = train_test_split(x, y, test_size=0.2, random_state=144, shuffle=True)
-
train_test_splitでデータを学習用と検証用に分割する -
test_size=0.2で学習用と検証用を8:2の割合で分割 -
random_stateは疑似乱数でこれを指定しないと、実行のたびに結果が変わってしまう
数字は自身のお好みの数字でどうぞ
-
shuffle=Trueで分割をシャッフルする
指定しない(False)場合、データの先頭から8割が学習用、残り2割が検証用として分割される
-
mean_squared_errorは予測精度を確認するために後で使う
なぜ検証用データを用意するのか?
学習用データとテスト用データのみで予測精度を評価した場合、テスト用データの予測に特化したモデルができてしまうため(過学習という)
例えば、ある年の1月から5月までのデータを使って天気を予測したい場合
テスト用のデータによる評価のみで予測精度を高める(過学習)と、その年の1月から5月までの天気は上手く予測できる
しかし、次の年の1月から5月の天気は前年とは異なり予測精度が悪くなる
これは、未知のデータに対して、予測できていないためである
検証用データを用意して、検証用とテスト用の2つのデータを同じくらいの精度で予測できるようにしておくと、未知のデータに対してある程度の精度を維持したまま予測することができる(過学習の防止)
過学習とは? - wiki
過剰適合(かじょうてきごう、英: overfitting)や過適合(かてきごう)や過学習(かがくしゅう、英: overtraining)とは、統計学や機械学習において、訓練データに対して学習されているが、未知データ(テストデータ)に対しては適合できていない、汎化できていない状態を指す。汎化能力の不足に起因する。
今回は、一番簡単なhold-out法を用いる
他にもクロスバリデーションやk-foldなど様々
予測結果の精度を描画する関数を定義
def predict_visualizer(valid, valid_predict, test, test_predict, title):
valid_array = np.array(valid)
test_array = np.array(test)
va_pred_array = np.array(valid_predict)
ts_pred_array = np.array(test_predict)
y_values = np.concatenate([valid_array, va_pred_array]).flatten()
ymin, ymax = np.amin(y_values), np.amax(y_values)
fig = plt.figure(figsize=(10, 10))
plt.scatter(valid_array, va_pred_array, label='valid', color='aqua', alpha=0.4)
plt.scatter(test_array, ts_pred_array, label='test', color='tomato', alpha=0.4)
plt.plot([ymin, ymax], [ymin, ymax])
plt.xlabel('test', fontsize=24)
plt.ylabel('predict', fontsize=24)
plt.title(f'{title}-Test-Predict Plot', fontsize=24)
plt.tick_params(labelsize=16)
plt.legend()
plt.show()
線形回帰の学習と予測精度の可視化(前処理なし)
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(x_train, y_train)
y_pred = lr.predict(x_valid)
y_pred_test = lr.predict(x_test)
print('='*20)
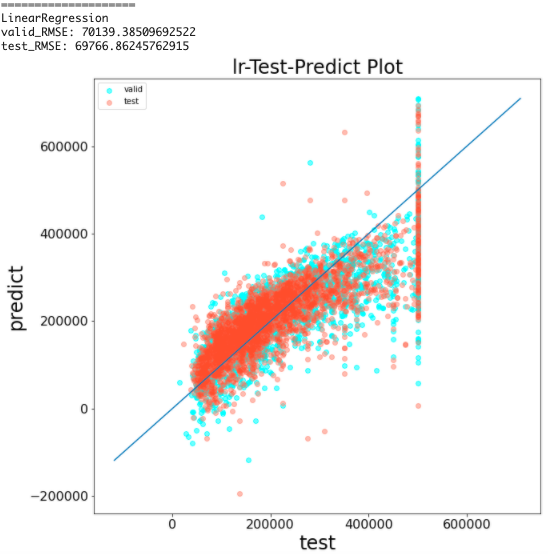
print('LinearRegression')
print(f'valid_RMSE: {np.sqrt(mean_squared_error(y_valid, y_pred))}')
print(f'test_RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_test))}')
predict_visualizer(y_valid, y_pred, y_test, y_pred_test, 'lr')
-
fitでモデルを学習させる -
predictで目的変数を予測する
今回は検証用とテスト用のデータ2つをそれぞれ予測する
予測精度を評価するために、今回はRMSE(Root Mean Squared Error)と呼ばれる平均平方2乗誤差を用いる
計算式は以下
$RMSE=\sqrt{\displaystyle\frac{1}{N}\sum_{i=1}^{n}(y_i-\hat{y_i})^2}$
$N$:予測対象データの総数
$y_i$:$i$番目の実際の値
$\hat{y_i}$:$i$番目の予測した値
mean_sqared_errorで平均2乗誤差を求め、np.sqrtで平方根をとる
結果から、RMSEは約7万となった
このモデルで住宅価格の予測を行なった場合、平均7万ドルの誤差で予測できることを意味している
散布図の見方として、青い直線に点が近いほど精度の高い予測であることを表す
この結果を見ると、testが500000の時、上手く予測できていない
これは外れ値の影響を強く受けているためだと考えられる
同様にして、他のモデルも見てみよう
XGBoostの学習と予測結果の可視化(前処理なし)
import xgboost as XGB
xgb = XGB.XGBRegressor(random_state=144)
xgb.fit(x_train, y_train)
y_pred = xgb.predict(x_valid)
y_pred_test = xgb.predict(x_test)
print('='*20)
print('XGBRegressor')
print(f'valid_RMSE: {np.sqrt(mean_squared_error(y_valid, y_pred))}')
print(f'test_RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_test))}')
predict_visualizer(y_valid, y_pred, y_test, y_pred_test, 'xgbr')
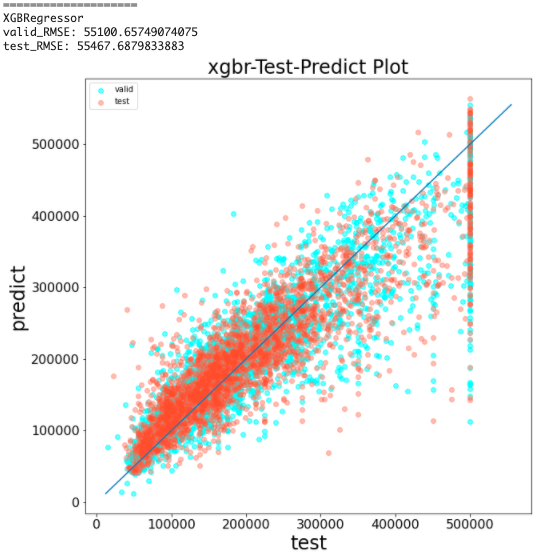
結果から、RMSEは約55000となった
線形回帰モデルよりも高い精度で予測できている
しかし、testが500000の時に上手く予測できていないことは同じである
ランダムフォレストの学習と予測結果の可視化(前処理なし)
from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(random_state=144, n_estimators=100)
rfr.fit(x_train, y_train)
y_pred = rfr.predict(x_valid)
y_pred_test = rfr.predict(x_test)
print('='*20)
print('RandomForestClassifier')
print(f'valid_RMSE: {np.sqrt(mean_squared_error(y_valid, y_pred))}')
print(f'test_RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_test))}')
predict_visualizer(y_valid, y_pred, y_test, y_pred_test, 'rfr')
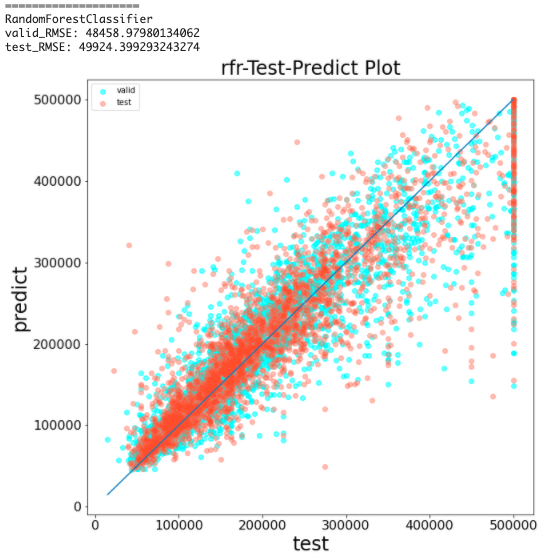
n_estimatorsで木の数を設定できる(今回は決め打ちで100)
結果から、RMSEは約49000となった
XGBoostよりも高い精度で予測できている
しかし、testが500000の時に上手く予測できていないことは同じである
ここまでで分かったこと - part2
| モデル | 検証用RMSE | テスト用RMSE |
|---|---|---|
| 線形回帰 | 70139 | 69766 |
| XGBoost | 55100 | 55100 |
| ランダムフォレスト | 48458 | 49924 |
- ランダムフォレストが一番精度の高い予測を行えている
-
testが500000の時の予測はどのモデルも上手くできていない
「ここまでで分かったこと - part1」でも述べた、外れ値が悪さをしているようだと予想できる
ここからは、前処理によって外れ値による影響を解消する
前処理
前処理する前に全てのデータ(trainとtest)を一つにまとめる
train_mid = train.copy()
test_mid = test.copy()
train_mid['train_test'] = 'train'
test_mid['train_test'] = 'test'
all_data = pd.concat([train_mid, test_mid]).reset_index(drop=True)
all_data.head()
-
copy()でtrainとtestのデータを汚さないようにする -
train_testカラムを追加 -
pd.concatで複数のDataFrameを結合 -
reset_indexでインデックスをリセット -
drop=Trueで元のインデックスを削除(これをしないと元のインデックスも含まれてしまう)
外れ値の確認
「ここまでで分かったこと - part1」の項目2.
housing_median_age、median_house_valueの最大値あたりが外れ値っぽい(ヒストグラムから)
を具体的に確認する
all_data['housing_median_age'].value_counts()
(結果一部省略)
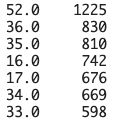
value_counts()でそれぞれの値の出現頻度を高い順に確認できる
結果から、最大値(describe参照)の52.0が最も多いことが分かる
median_house_valueカラムも確認する
all_data['median_house_value'].value_counts()
(結果一部省略)
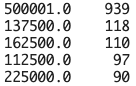
結果から、最大値の500001.0が最も多いことが分かる
2つの結果から、それぞれの最大値が外れ値であることが分かり、予測精度に悪影響を及ぼしていると考えられる
外れ値の削除
それぞれの最大値を削除する
all_data = all_data.query(' housing_median_age < 52 and median_house_value < 500000 ').reset_index(drop=True)
queryで条件に一致する行のみ抽出できる
抽出によってインデックスが飛び飛びになるのでreset_indexを忘れずに
describeやhistでどのように変わったか確認してみよう!
※KaggleやSIGNATEなどの分析コンペでは、testデータを削除してはいけない
分析コンペの場合、学習用データの外れ値のみ削除する
all_dataをtrainとtestに分割
外れ値を削除する前処理が終わったので、trainとtestに分割
train = all_data.query(" train_test == 'train' ").drop('train_test', axis=1)
test = all_data.query(" train_test == 'test' ").drop('train_test', axis=1)
モデルの学習と予測 - part2
「モデルの学習と予測 - part1」とほとんど同じように進める
データを学習用・検証用・テスト用に分割
part1の処理と同じ
x_test = test.drop(obj_var, axis=1)
y_test = test[obj_var]
x = train.drop(obj_var, axis=1)
y = train[obj_var]
x_train, x_valid, y_train, y_valid = train_test_split(x, y, test_size=0.2, random_state=144, shuffle=True)
標準化
線形モデルでは標準化が必要
「モデルの学習と予測 - part1」では敢えて行わなかった
from sklearn.preprocessing import StandardScaler
std_scl = StandardScaler()
x_train = std_scl.fit_transform(x_train)
x_valid = std_scl.transform(x_valid)
x_test = std_scl.transform(x_test)
StandardScalarメソッドの詳細は以下
線形回帰の学習と予測精度の可視化(前処理あり)
part1の処理と同じ
lr = LinearRegression()
lr.fit(x_train, y_train)
y_pred = lr.predict(x_valid)
y_pred_test = lr.predict(x_test)
print('='*20)
print('LinearRegression')
print(f'valid_RMSE: {np.sqrt(mean_squared_error(y_valid, y_pred))}')
print(f'test_RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_test))}')
predict_visualizer(y_valid, y_pred, y_test, y_pred_test, 'lr')
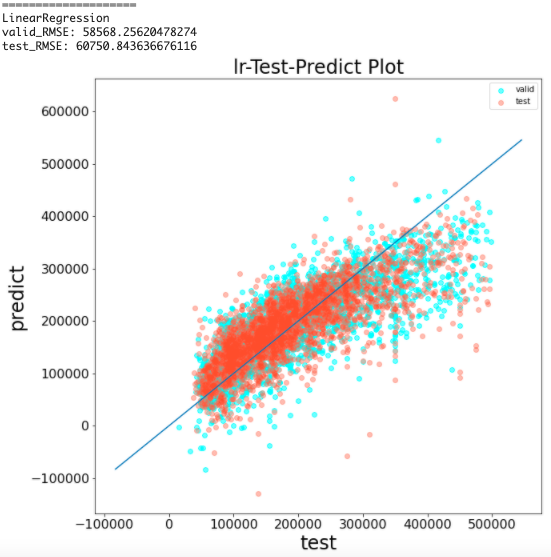
結果から、RMSEは約6万となった
part1では約7万だったため、精度が良くなっている
XGBoostの学習と予想精度の可視化(前処理あり)
part1の処理と同じ
xgb = XGB.XGBRegressor(random_state=144)
xgb.fit(x_train, y_train)
y_pred = xgb.predict(x_valid)
y_pred_test = xgb.predict(x_test)
print('='*20)
print('XGBRegressor')
print(f'valid_RMSE: {np.sqrt(mean_squared_error(y_valid, y_pred))}')
print(f'test_RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_test))}')
predict_visualizer(y_valid, y_pred, y_test, y_pred_test, 'xgbr')
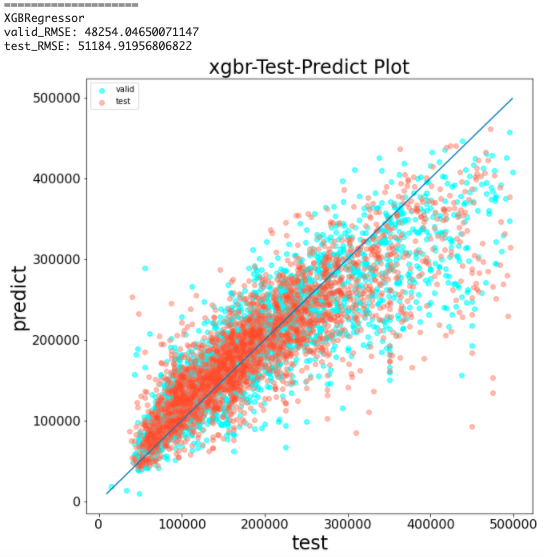
結果から、RMSEは約5万となった
part1では約55000だったため、精度が良くなっている
ランダムフォレストの学習と予測精度の可視化(前処理あり)
part1の処理と同じ
rfr = RandomForestRegressor(random_state=144, n_estimators=100)
rfr.fit(x_train, y_train)
y_pred = rfr.predict(x_valid)
y_pred_test = rfr.predict(x_test)
print('='*20)
print('RandomForestClassifier')
print(f'valid_RMSE: {np.sqrt(mean_squared_error(y_valid, y_pred))}')
print(f'test_RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_test))}')
predict_visualizer(y_valid, y_pred, y_test, y_pred_test, 'rfr')
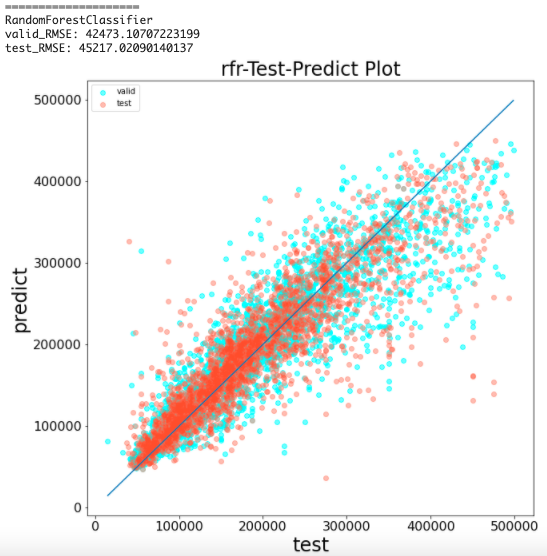
結果から、RMSEは約45000となった
part1では約49000だったため、精度が良くなっている
まとめ
- Google Colaboratoryで機械学習をやってみた
-
california_housingデータを確認 - 前処理なしと前処理ありで予測精度の比較を行なった
- 前処理を行なって学習したモデルの予測精度が向上したことを確認した
part1結果
| モデル | 検証用RMSE | テスト用RMSE |
|---|---|---|
| 線形回帰 | 70139 | 69766 |
| XGBoost | 55100 | 55100 |
| ランダムフォレスト | 48458 | 49924 |
part2結果
| モデル | 検証用RMSE | テスト用RMSE |
|---|---|---|
| 線形回帰 | 58568 | 60750 |
| XGBoost | 48254 | 51184 |
| ランダムフォレスト | 42473 | 45217 |
今回行った前処理は外れ値の削除のみだった
しかし、前処理が全行程の8割を占めると言われるデータ分析ではまだまだ改善すべき問題が残っている
これを機に少しでもデータ分析に興味が湧いたなら、より良い予測精度を求めて他の前処理を試してみて欲しい