9軸IMUによる姿勢推定
何番煎じか分からないが、拡張カルマンフィルタ (EKF) を用いて3次元空間での姿勢推定を実装する。
- 加速度センサ
- ジャイロセンサ
- 地磁気センサ
上記の3つのセンサから得られるデータを用いて、3次元空間における姿勢推定を行う。
今回の実装における推定結果はオイラー角 Z-Y-X系として得られる。
1つのセンサのみからでもある程度の姿勢を計算することできる。
が、複数のセンサを用いてより高精度な姿勢を得ることが今回の目的である。
細かいところは触れず、まずは一通りの計算を行うことを目指す。
各センサからの姿勢推定
それぞれのセンサによる姿勢推定の方法は、下記の記事にまとめている。
細かな導出方法は下記を参照してほしい。
加速度センサでオイラー角の姿勢推定 - Qiita
ジャイロセンサでオイラー角の姿勢推定 - Qiita
地磁気センサでオイラー角の姿勢推定 - Qiita
前提条件
座標軸
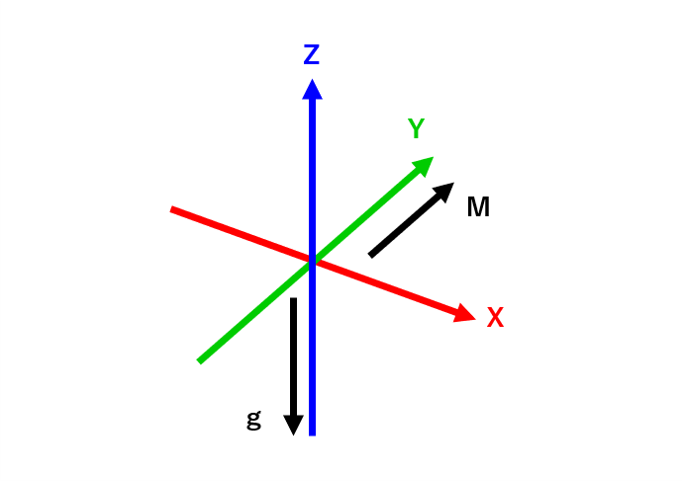
下図のような座標軸を基準に計算を進めていく。
z軸を上向き、重力方向をz軸の反対方向、地磁気方向 (北) をy軸と同一方向に設定。
オイラー角の系
今回の考えるオイラー角の系を、Z-Y-X系として計算する。
オイラー角の表現は$\boldsymbol{(\theta_x, \theta_y, \theta_z )}$の順で記載する.
例として、Z-Y-X系の$(\gamma , \beta, \alpha )$ が与えられた場合を考える。
- 初期の座標系を x-y-z とする
- z 軸周りで α 回転する
- 回転後のy' 軸周りで β 回転する
- 回転後のx'' 軸周りで γ 回転する
拡張カルマンフィルタ
・カルマンフィルタについて
あまり詳しいことは知らないので、下記の記事らを参考にしてほしい。
良くまとまっている記事を上げておく。
多分、大事なことは下記の3点。
- 現在の状態から1つ先の未来の状態を予測する。 ( $x_{t\_a} = A\ $ )
- 外部からの観測値による状態を計算する。 ( $x_{t\_b} = B\ $ )
- 足して1になるように係数をかける。 ( $x_t = kA + (1-k)B$ )
2つの状態を計算してその間を取る、ような感覚。
信頼性性の高い方の係数を大きくすることで、フィルタリングの精度を変更することが可能。
拡張カルマンフィルタの手順
・事前準備
- 推定対象の状態を設定:$\boldsymbol{x}$
- 推定対象の分散を設定:$\boldsymbol{\sigma^2}$
- 状態予測モデルを作成:$\boldsymbol{\hat{x}}$
- 状態観測モデルを作成:$\boldsymbol{\tilde{x}}$
- 状態遷移ノイズを設定:$\boldsymbol{Q}$
- 状態観測ノイズを設定:$\boldsymbol{R}$
・繰り返し計算
- 過去の状態から現在の状態を予測:$\boldsymbol{\hat{x}}$
- 観測値から現在の状態を予測:$\boldsymbol{\tilde{x}}$
- 予測状態のヤコビ行列を計算:$\boldsymbol{A}$
- 観測状態のヤコビ行列を計算:$\boldsymbol{C}$
- 予測分散を計算:$\boldsymbol{\sigma^2_Q}\ $
- 観測分散を計算:$\boldsymbol{\sigma^2_R}\ $
- カルマンゲインを計算:$\boldsymbol{K}$
- 推定対象の状態を更新:$\boldsymbol{x}$
- 推定対象の分散を更新:$\boldsymbol{\sigma^2}$
各単語の意味
上記に登場する単語の意味と設定内容を簡単に記載。
- 推定対象の状態 $\boldsymbol{x}$:求めたい値
- 推定対象の分散 $\boldsymbol{\sigma^2}$:求めたい値の分散
- 状態予測モデル $\boldsymbol{\hat{x}}$:状態を予測するときの計算式
- 状態観測モデル $\boldsymbol{\tilde{x}}$:観測値から状態を計算するときの計算式
- 状態遷移ノイズ $\boldsymbol{Q}$:状態の予測に含まれるノイズ
- 状態観測ノイズ $\boldsymbol{R}$:観測値からの状態の計算に含まれるノイズ
- 予測状態のヤコビ行列 $\boldsymbol{A}$:状態予測モデル$\boldsymbol{\hat{x}}$ の偏微分行列
- 観測状態のヤコビ行列 $\boldsymbol{C}$:状態予測モデル$\boldsymbol{\tilde{x}}$ の偏微分行列
- 予測分散 $\boldsymbol{\sigma^2_Q}$:状態を予測したときの分散
- 観測分散 $\boldsymbol{\sigma^2_R}$:観測値から状態を計算したときの分散
- カルマンゲイン$\boldsymbol{K}$:予測した状態と計算した状態の信頼性の割合
事前準備
1. 推定対象の状態を設定:$\boldsymbol{x}$
推定したい状態を設定する。
ここでは3次元空間における姿勢、ZYX系オイラー角を求めることとする。
初期値は全て0に設定する。
\begin{align}
&\boldsymbol{x} = (\theta_x, \theta_y, \theta_z) \\
&\boldsymbol{x_0} = (0,0,0)
\end{align}
2. 推定対象の分散を設定:$\boldsymbol{\sigma^2}$
状態変数の共分散行列を設定する。
ここでは、状態変数はそれぞれ独立しているとする。
\boldsymbol{\sigma^2} =
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}
共分散についてk知りたい方は下記記事が参考になると思う。
共分散行列とは?(定義、意味、分布の推定) - Qiita
3. 状態予測モデルを作成:$\boldsymbol{\hat{x}}$
時間 t-1 の状態 $\ \boldsymbol{x_{t-1}}$ から時間 t の状態 $\boldsymbol{x_t}$ を予測するための計算式を作成する。
今回の場合、予測にはジャイロセンサのデータを使用する。
基本的には、ジャイロセンサから姿勢を計算するだけの方程式である。
ジャイロセンサでオイラー角の姿勢推定 - Qiita
ジャイロセンサから得られた値を $\boldsymbol{\omega} = (\omega_x,\omega_y,\omega_z)$ とする。
前の状態から現在の状態までの時間間隔を $\Delta T$ とする。
\begin{pmatrix}
\hat{\theta}_x \\ \hat{\theta}_y \\ \hat{\theta}_z
\end{pmatrix}
= \begin{pmatrix}
\theta_x \\ \theta_y \\ \theta_z
\end{pmatrix}
+ \begin{pmatrix}
1 & \tan \theta_y \sin \theta_x & \tan \theta_y \cos \theta_x \\
0 & \cos \theta_x & -\sin \theta_x \\
0 & \frac{\sin \theta_x}{\cos \theta_y} & \frac{\cos \theta_x}{\cos \theta_y}
\end{pmatrix}
\begin{pmatrix}
\omega_{x} \\ \omega_{y} \\ \omega_{z}
\end{pmatrix}
\Delta T \
展開すると下記のようになる。(後で使う)
\begin{align}
&\hat{\theta}_x = \theta_x + (\omega_x + \omega_y \tan \theta_y \sin \theta_x + \omega_z \tan \theta_y \cos \theta_x)\Delta T \\
&\hat{\theta}_y = \theta_y + (\omega_y \cos \theta_x - \omega_z \sin \theta_x )\Delta T \\
&\hat{\theta}_z = \theta_z + (\omega_y {\scriptsize \frac{\sin \theta_x}{\cos \theta_y}} + \omega_z {\scriptsize \frac{\cos \theta_x}{\cos \theta_y}} )\Delta T
\end{align}
これはジャイロの観測値を使用しているのに予測モデルなのだろうか。
一刻前の状態を用いているから予想モデルなのだろう、うん。
4. 状態観測モデルを作成:$\boldsymbol{\tilde{x}}$
センサからの観測値を用いて現在の状態を求める計算式を作成する。
今回の場合、計算には加速度センサと地磁気センサのデータを用いる。
基本的には、加速度センサと地磁気センサから姿勢を計算するだけの方程式である。
加速度センサでオイラー角の姿勢推定 - Qiita
地磁気センサでオイラー角の姿勢推定 - Qiita
加速度センサから得られた値を $\boldsymbol{a} = (a_x, a_y, a_z)$ とする。
地磁気センサから得られた値を $\boldsymbol{m} = (m_x, m_y, m_z)$ とする。
\begin{align}
&\tilde{\theta}_x = \tan^{-1}\biggl(\frac{-a_y}{-a_z}\biggl) \\
&\tilde{\theta}_y = \tan^{-1}\biggl(\frac{a_x}{\sqrt{a_y^2+a_z^2}}\biggl) \\
&\tilde{\theta}_z = \tan^{-1}\biggl(\frac{m_x \cos \tilde{\theta}_y + m_y \sin \tilde{\theta}_y \sin \tilde{\theta}_x + m_z \sin \tilde{\theta}_y \cos \tilde{\theta}_x}{m_y \cos \tilde{\theta}_x - m_z \sin \tilde{\theta}_x} \biggl)
\end{align}
\\
5. 状態遷移ノイズを設定:$\boldsymbol{Q}$
時間 t-1 の状態 $\ \boldsymbol{x_{t-1}}$ から時間 t の状態 $\boldsymbol{x_t}$ を予測したときのノイズを設定する。
予測にはジャイロセンサのデータを使用しているため、ノイズは比較的小さいと考える。
また、各軸のノイズは独立しているとする。
\boldsymbol{Q} =
\frac{1}{100}
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}
\\
6. 状態観測ノイズを設定:$\boldsymbol{R}$
センサからの観測値を用いて現在の状態を計算したときのノイズを設定する。
計算には加速度センサと地磁気センサのデータを使用しているため、ノイズは比較的大きいと考える。
また、各軸のノイズは独立しているとする。
\boldsymbol{R} =
\frac{1}{10}
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}
\\
繰り返し計算
1. 過去の状態から現在の状態を予測:$\boldsymbol{\hat{x}}$
事前準備の 3. で用意した状態予測モデルで現在の状態を予測する。
\begin{align}
&\boldsymbol{\hat{x}} =
\begin{pmatrix}
\hat{\theta}_x \\ \hat{\theta}_y \\ \hat{\theta}_z
\end{pmatrix} \\
\\
&\hat{\theta}_x = \theta_x + (\omega_x + \omega_y \tan \theta_y \sin \theta_x + \omega_z \tan \theta_y \cos \theta_x)\Delta T \\
&\hat{\theta}_y = \theta_y + (\omega_y \cos \theta_x - \omega_z \sin \theta_x )\Delta T \\
&\hat{\theta}_z = \theta_z + (\omega_y {\scriptsize \frac{\sin \theta_x}{\cos \theta_y}} + \omega_z {\scriptsize \frac{\cos \theta_x}{\cos \theta_y}} )\Delta T
\end{align}
2. 観測値から現在の状態を計算:$\boldsymbol{\tilde{x}}$
事前準備の 4. で用意した観測モデルで現在の状態を計算する。
\begin{align}
&\boldsymbol{\tilde{x}} =
\begin{pmatrix}
\tilde{\theta}_x \\ \tilde{\theta}_y \\ \tilde{\theta}_z
\end{pmatrix} \\
\\
&\tilde{\theta}_x = \tan^{-1}\biggl(\frac{-a_y}{-a_z}\biggl) \\
&\tilde{\theta}_y = \tan^{-1}\biggl(\frac{a_x}{\sqrt{a_y^2+a_z^2}}\biggl) \\
&\tilde{\theta}_z = \tan^{-1}\biggl(\frac{m_x \cos \tilde{\theta}_y + m_y \sin \tilde{\theta}_y \sin \tilde{\theta}_x + m_z \sin \tilde{\theta}_y \cos \tilde{\theta}_x}{m_y \cos \tilde{\theta}_x - m_z \sin \tilde{\theta}_x} \biggl)
\end{align}
3. 予測状態のヤコビ行列を計算:$\boldsymbol{A}$
予測モデルのヤコビ行列 (偏微分行)を計算する。
\boldsymbol{A}
= \frac{d \boldsymbol{\hat{x}}}{d \boldsymbol{x}}
= \begin{pmatrix}
\large \frac{\partial \hat{\theta}_x}{\partial \theta_x}
& \large \frac{\partial \hat{\theta}_x}{\partial \theta_y}
& \large \frac{\partial \hat{\theta}_x}{\partial \theta_z} \\
\large \frac{\partial \hat{\theta}_y}{\partial \theta_x}
& \large \frac{\partial \hat{\theta}_y}{\partial \theta_y}
& \large \frac{\partial \hat{\theta}_y}{\partial \theta_z} \\
\large \frac{\partial \hat{\theta}_z}{\partial \theta_x}
& \large \frac{\partial \hat{\theta}_z}{\partial \theta_y}
& \large \frac{\partial \hat{\theta}_z}{\partial \theta_z}
\end{pmatrix} \\
\\
\begin{align}
&\frac{\partial \hat{\theta}_x}{\partial \theta_x} = 1 + (\omega_x + \omega_y \tan \theta_y \cos \theta_x - \omega_z \tan \theta_y \sin \theta_x)\Delta T \\
&\frac{\partial \hat{\theta}_x}{\partial \theta_y} = (\omega_y \frac{\sin \theta_x}{\cos^2 \theta_y} + \omega_z \frac{\cos \theta_x}{\cos^2 \theta_y})\Delta T \\
&\frac{\partial \hat{\theta}_x}{\partial \theta_y} = 0 \\
\\
&\frac{\partial \hat{\theta}_y}{\partial \theta_x} = (-\omega_y \sin \theta_x - \omega_z \cos \theta_x )\Delta T \\
&\frac{\partial \hat{\theta}_y}{\partial \theta_y} = 1 \\
&\frac{\partial \hat{\theta}_y}{\partial \theta_z} = 0 \\
\\
&\frac{\partial \hat{\theta}_z}{\partial \theta_x} = (\omega_y \frac{\cos \theta_x}{\cos \theta_y} - \omega_z \frac{\sin \theta_x}{\cos \theta_y} )\Delta T \\
&\frac{\partial \hat{\theta}_z}{\partial \theta_y} = (\omega_y \sin \theta_x \frac{\sin \theta_y}{\cos^2 \theta_y} + \omega_z \cos \theta_x \frac{\sin \theta_y}{\cos^2 \theta_y})\Delta T \\
&\frac{\partial \hat{\theta}_z}{\partial \theta_z} = 1
\end{align}
\\
4. 観測状態のヤコビ行列を計算:$\boldsymbol{C}$
観測モデルのヤコビ行列 (偏微分行)を計算する。
\boldsymbol{C}
= \frac{d \boldsymbol{\tilde{x}}}{d \boldsymbol{x}}
= \begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}
人によっては、$\boldsymbol{C} = \boldsymbol{0}\ $ と設定している方法もある。 (計算式に $\theta$ が含まれないため)
私の環境だと0行列では上手く計算できなかった。 (後のカルマンゲインが 0 になるため)
そのため、ここではヤコビ行列を単位行列としている。
5. 予測分散を計算:$\boldsymbol{\sigma^2_Q}$
一刻前の状態の分散、状態遷移ノイズ、予測モデルのヤコビ行列を用いて予測分散を計算する。
\boldsymbol{\sigma^2_Q} = \boldsymbol{A}\boldsymbol{\sigma^2}\boldsymbol{A}^T+\boldsymbol{Q}
6. 観測分散を計算:$\boldsymbol{\sigma^2_R}$
予測分散、観測ノイズ、観測モデルのヤコビ行列を用いて観測分散を計算する。
\boldsymbol{\sigma^2_R} = \boldsymbol{C}\boldsymbol{\sigma^2_Q}\boldsymbol{C}^T+\boldsymbol{R}
7. カルマンゲインを計算:$\boldsymbol{K}$
予測分散、観測分散、観測モデルのヤコビ行列を用いてカルマンゲインを計算する。
\boldsymbol{K} = \boldsymbol{\sigma^2_Q}\boldsymbol{C}^T(\boldsymbol{\sigma^2_R})^{-1}
8. 推定対象の状態を更新:$\boldsymbol{x}$
カルマンゲインを用いて現在の状態を更新する。
\boldsymbol{x} = \boldsymbol{\hat{x}} + \boldsymbol{K}(\boldsymbol{\tilde{x}} - \boldsymbol{C}\boldsymbol{\hat{x}} )
9. 推定対象の分散を更新:$\boldsymbol{\sigma^2}$
カルマンゲインを用いて現在の状態の分散を更新する。
\boldsymbol{\sigma^2} = (\boldsymbol{I} - \boldsymbol{K}\boldsymbol{C})\boldsymbol{\sigma^2_Q}
\\
1~9 までの計算後、新たな観測値を取得したらまた 1~9 の計算を繰り返す。
実装結果
上記の内容を実装した結果を下記に示す。
IMUは下記のセンサを使用。50Hz で観測値を取得。
LSM9DS1使用9軸センサモジュール - 秋月電子
プログラムはC#、表示はUnityで実装。
ベクトルや行列の計算ができれば何でもいい。
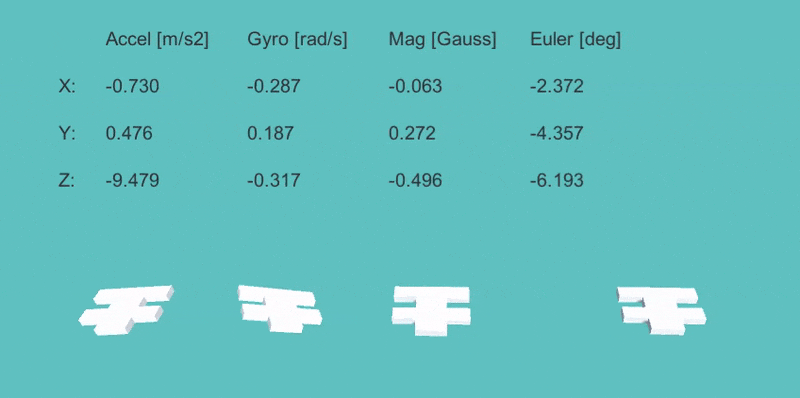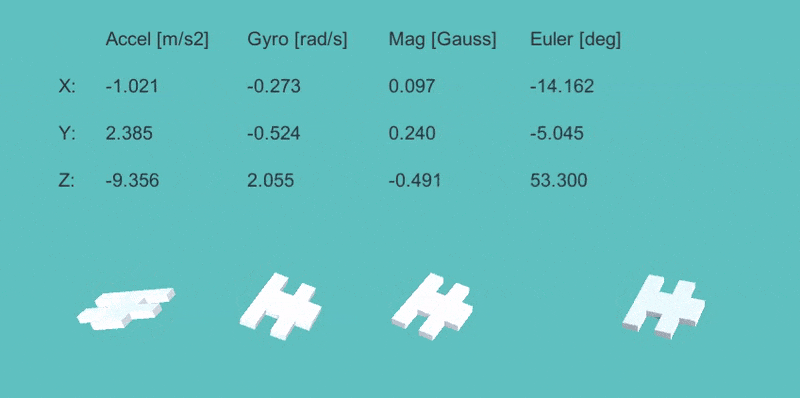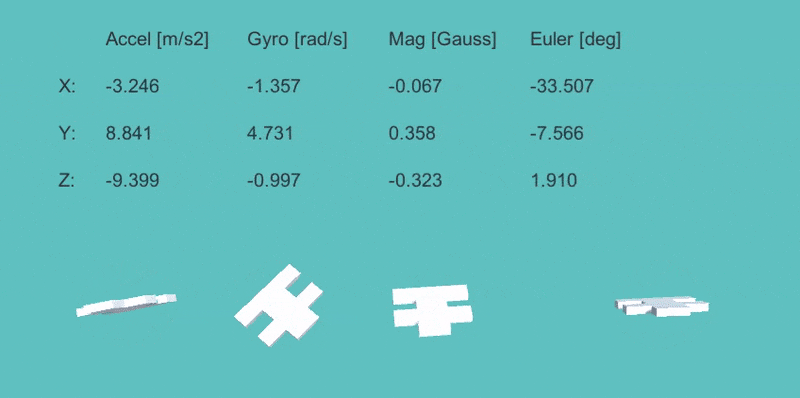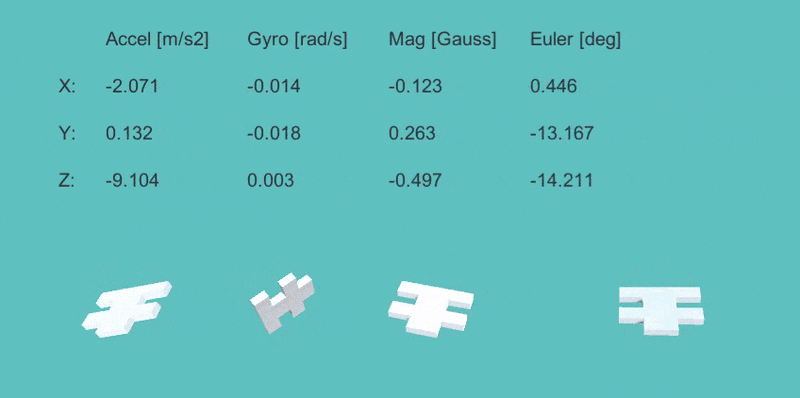
上の数値は左から、「加速度の観測値」「ジャイロの観測値」「地磁気の観測値」「9軸EKFでの姿勢(オイラー角)」の値。
下のモデルは左から、「加速度のみ」「ジャイロのみ」「地磁気のみ」「9軸EKF」による姿勢の計算結果を表示。
ポイント
- 加速度センサと地磁気センサによる姿勢推定は、センサのブレに弱いが姿勢の絶対値を取得可能。
- ジャイロセンサによる姿勢推定は、センサのブレに強いが姿勢の累積誤差によりズレが大きくなってく。
- 9軸EKF による姿勢推定は、ブレに強いジャイロセンサと、絶対値を取得可能な加速度センサと地磁気センサの良いとこ取り。
課題
-
9軸EKFを用いても、思っていたよりはキレイに姿勢を計算できていない。
- カルマンフィルタの基礎が疎かなまま実装しているため。
- 状態遷移ノイズや観測ノイズの設定がテキトーすぎるため。
-
角度が90度付近では姿勢が不安定。
- オイラー角で計算しているためジンバルロックの問題がある。
- クォータニオンによる9軸EKFは未着手。
-
IMUのセンサフュージョンには他にmadgwickフィルタ等もあるが、未着手。
以上です。
おかしな部分や間違っている部分もあると思うので、何かあればコメントください。
参考ページ
カルマンフィルタを用いた姿勢推定 - Qiita
6軸IMUを使ってオイラー角に対してEKFを組んでみた - Qiita
mbedとrosでドローンを飛ばす(5)~拡張カルマンフィルタによる姿勢推定~ - Qiita
Pythonで拡張カルマンフィルタを実装してみる
カルマンフィルタについて - こうきょの日記