mbedとrosでドローンを飛ばす(5)~拡張カルマンフィルタによる姿勢推定~

こんにちは。takepiyoです。今回はドローンの姿勢推定アルゴリズムの実装をします

状態方程式

$\phi, \theta, \psi$をグローバルな座標系から見たロール・ピッチ・ヨーのオイラー角,$\omega_x, \omega_y, \omega_z$を加速度センサの座標系から見たx,y,z軸の角速度としたとき、状態方程式は以下のように表されます。

\begin{bmatrix}
\dot{\phi}\\
\dot{\theta}\\
\dot{\psi}
\end{bmatrix}
=
\begin{bmatrix}
1 & \sin\phi\tan\theta & \cos\phi\tan\theta \\
0 & \cos\phi & -\sin\phi \\
0 & \frac{\sin\phi}{\cos\theta} & \frac{\cos\phi}{\cos\theta}
\end{bmatrix}

\begin{bmatrix}
\omega_x \\
\omega_y \\
\omega_z \\
\end{bmatrix}

観測方程式

$a_x, a_y, a_z$をセンサから得られる加速度、重力加速度を$g$すると観測方程式は以下のようにあわらされます。(鉛直下向きを正とする)

\begin{bmatrix}
a_x \\
a_y \\
a_z \\
\end{bmatrix}
=
\begin{bmatrix}
-g\sin\theta \\
g\cos\theta\sin\phi \\
g\cos\theta\cos\phi
\end{bmatrix}

これにより$\phi$と$\theta$を加速度から求めることができます。

\begin{bmatrix}
\phi \\
\theta
\end{bmatrix}
=
\begin{bmatrix}
\tan^{-1}\frac{a_y}{a_z} \\
-\tan^{-1}\frac{a_x}{\sqrt{a_y^2+a_z^2}}
\end{bmatrix}

ヨー角の変化は重力加速度の分量を変化させないので、加速度からヨー角を求めることはできません。後述する拡張カルマンフィルタは、２つの方法で値を推定できないと使えないのでヨー角には使えないことが分かります。

状態空間モデルと観測方程式の定義

実際に得られる加速度と角速度にはノイズが含まれており、正しい姿勢を計算することができません。そのノイズの影響を最小化して正しい値を推定するのがカルマンフィルタです。
状態方程式が非線形なのでヤコビアンで近似を行います。この場合のカルマンフィルタを拡張カルマンフィルタと呼ぶようです。
前述の通り、ヨー角にはカルマンフィルタを適用できないので、推定量$\hat{x}$を
$$\hat{\boldsymbol{x_{n}}} = [\phi_{n} ;; \theta_{n}]^T$$
と定義します。また、真の値を装飾なし$\boldsymbol{x}$で表すと、離散化された状態方程式は以下のようになります。

\begin{align}
\boldsymbol{x_{n}} &= \boldsymbol{x_{n-1}}+\dot{\boldsymbol{x_n}}\Delta t + \begin{bmatrix} N(0, q_1) \\ N(0, q_2) \end{bmatrix} \\
&= \begin{bmatrix} \phi_{n-1} + \Delta t (\omega_x + \omega_y\sin\phi_{n-1}\tan\theta_{n-1} + \omega_z\cos\phi_{n-1}\tan\theta_{n-1}) \\ \theta_{n-1} + \Delta t(\omega_y\cos\phi_{n-1}-\omega_z\sin\phi_{n-1}) \end{bmatrix} + \begin{bmatrix} N(0, q_1) \\ N(0, q_2) \end{bmatrix}
\end{align}\\
\boldsymbol{x_{n}} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\boldsymbol{x_{n}}

$N(0, q_1), N(0, q_2) $は互いに独立な正規分布(ノイズ)です。今回の状態方程式の場合、3行目の式が単位行列で表現できるので意味がありませんが、ほかのモデルの場合この行列が単位行列でない場合があるのでそれを意識するために一応書いておきました。この行列はあとに出てくる$\boldsymbol{H}$です。

観測方程式は

\boldsymbol{y_n}
=
\begin{bmatrix}
\tan^{-1}\frac{a_y}{a_z} \\
-\tan^{-1}\frac{a_x}{\sqrt{a_y^2+a_z^2}}
\end{bmatrix}
+
\begin{bmatrix} N(0, r_1) \\ N(0, r_2) \end{bmatrix}

$N(0, r_1), N(0, r_2) $は互いに独立な正規分布(ノイズ)です。

拡張カルマンフィルタ

パラメータ初期化

ノイズの分散の値を決め(後でチューニングするべき？)、更に推定量や共分散行列の初期化を行います。

q_1 = q_2 = \sqrt{1.74} \times 10^{-1} \times \Delta t \\
\boldsymbol{Q} = \begin{bmatrix}q_1^2 & 0 \\ 0 & q_2^2 \end{bmatrix} \\
r_1 = r_2 = 1.0 \times \Delta t \\
\boldsymbol{R} = \begin{bmatrix}r_1^2 & 0 \\ 0 & r_2^2 \end{bmatrix} \\
\boldsymbol{\hat{x_{0}}} = \begin{bmatrix}0.0\\0.0 \end{bmatrix} \\
\boldsymbol{\hat{P_0}}= \boldsymbol{Q} \\

$\boldsymbol{Q}$と$\boldsymbol{R}$は共分散行列です。非対角成分は$(q_1,q_2)$,$(r_1,r_2)$がそれぞれ互いに独立であることから$0$となります。

状態値、共分散行列予測

\boldsymbol{\bar{x}_n} = \begin{bmatrix} \phi_{n-1} + \Delta t (\omega_x + \omega_y\sin\phi_{n-1}\tan\theta_{n-1} + \omega_z\cos\phi_{n-1}\tan\theta_{n-1}) \\ \theta_{n-1} + \Delta t(\omega_y\cos\phi_{n-1}-\omega_z\sin\phi_{n-1}) \end{bmatrix} \\

\boldsymbol{\bar{P}_n} = \boldsymbol{\hat{F}_{t-1}}\boldsymbol{\hat{P}_{n-1}}\boldsymbol{\hat{F}_{n-1}^T} + \boldsymbol{Q}

ここで$\boldsymbol{F}$は

\boldsymbol{f(\boldsymbol{x})}=\begin{bmatrix} \phi + \Delta t (\omega_x + \omega_y\sin\phi\tan\theta + \omega_z\cos\phi\tan\theta) \\ \theta + \Delta t(\omega_y\cos\phi-\omega_z\sin\phi) \end{bmatrix} \\

としたときのヤコビアンです。

\begin{align}
\boldsymbol{F_{t-1}}&=\frac{\partial\boldsymbol{f(\boldsymbol{x})}}{\partial\boldsymbol{x}}|_{\boldsymbol{x}=\boldsymbol{\hat{x}_{n-1}}} \\
&=
\begin{bmatrix} 
1 + \Delta t (\cos\phi_{n-1}\tan\theta_{n-1}\omega_y-\sin\phi_{n-1}\tan\theta_{n-1}\omega_z) & \Delta t (\frac{\sin\phi_{n-1}}{\cos^2\theta_{n-1}}\omega_y+\frac{\cos\phi_{n-1}}{\cos^2\theta_{n-1}}\omega_z) \\
-\Delta t(\sin\phi_{n-1}\omega_y + \cos\theta_{n-1}\omega_z) & 1
\end{bmatrix}　
\end{align}

カルマンゲイン、状態値、共分散行列更新

\boldsymbol{K_n}=\boldsymbol{\bar{P}_n}\boldsymbol{H^T_n}(\boldsymbol{H_n}\boldsymbol{\bar{P_n}}\boldsymbol{H_n^T}+\boldsymbol{R})^{-1}\\
\boldsymbol{\hat{x}_n}=\boldsymbol{\hat{x}_n} + \boldsymbol{K_n}(\boldsymbol{y_n}-\boldsymbol{H_n}\boldsymbol{\bar{x}_n})\\
\boldsymbol{\hat{P}_n}=(\boldsymbol{I}-\boldsymbol{K_n}\boldsymbol{H_n})\boldsymbol{\bar{P_n}}

実装

クラスで書いてみました

ExtendedKalmanFilter.cpp

#include "ExtendedKalmanFilter.h"
#include "Eigen/Dense.h"
using namespace Eigen;
using namespace std;

#include <ros.h>
#include <geometry_msgs/Vector3.h>

Ekf::Ekf(double delta_t)
{
  this->_delta_t = delta_t;
  this->_covariance_q << 1.74E-2*delta_t*delta_t, 0,
                         0                      , 1.74E-2*delta_t*delta_t;
  this->_covariance_r << 1.00*delta_t*delta_t, 0,
                         0                      , 1.00*delta_t*delta_t;
  this->_covariance_p = this->_covariance_q;
  this->_roll_pitch << 0.0,
                  0.0;
  this->_yaw = 0.0;
  this->_observation_matrix_H << 1.0, 0.0,
                                 0.0, 1.0;
}

Ekf::~Ekf()
{

}

geometry_msgs::Vector3 Ekf::get_corrected(const geometry_msgs::Vector3& linear_acc,
                                          const geometry_msgs::Vector3& angular_vel)
{
  this->_linear_acc << linear_acc.x,
                       linear_acc.y,
                       linear_acc.z;

  this->_angular_vel << angular_vel.x,
                        angular_vel.y,
                        angular_vel.z;

  Matrix<double, 2, 1> pre_angle = _predict_angle();
  Matrix<double, 2, 2> state_jacobian_F = _get_state_jacobian();
  Matrix<double, 2, 2> pre_covariance_p = _predict_covariance_p(state_jacobian_F);
  
  Matrix<double, 2, 1> actual_observation_angle = _get_actual_observation_angle();

  //  Because observatio matrix H is identity, pre_angle is able to be used as pred_observation_angle
  Matrix<double, 2, 2> kalman_gain = _get_kalman_gain(pre_covariance_p);
  _update_covariance_p(kalman_gain, pre_covariance_p);
  return _get_corrected_angle(pre_angle, actual_observation_angle, kalman_gain);
}

 Matrix<double, 3, 2> Ekf::_get_trigonometric(const Matrix<double, 2, 1>& angle)
{
  Matrix<double, 3, 2> trigonometric;
  trigonometric << sin(angle(0)), sin(angle(1)), 
                   cos(angle(0)), cos(angle(1)), 
                   tan(angle(0)), tan(angle(1));
  return trigonometric;
}

Matrix<double, 2, 1> Ekf::_predict_angle()
{
  Matrix<double, 3, 2> tri;
  tri = _get_trigonometric(this->_roll_pitch);
  Matrix<double, 2, 3> A;
  A << 1.0, tri(0, 0) * tri(2, 1), tri(1, 0) * tri(2, 1),
       0.0, tri(1, 0)            , -1.0 * tri(0, 1); 
  Matrix<double, 2, 1> pred_angle;
  pred_angle = this->_roll_pitch + this->_delta_t * (A * this->_angular_vel);

  // predict yaw angle here to minimize tri calcurate
  this->_yaw += this->_delta_t * ((this->_angular_vel(1) * tri(0, 0)) / tri(1, 1) + (this->_angular_vel(2) * tri(1, 0)) / tri(1, 1));
  return pred_angle;
}

Matrix<double, 2, 2> Ekf::_get_state_jacobian()
{
  Matrix<double, 3, 2> tri;
  tri = _get_trigonometric(this->_roll_pitch);
  Matrix<double, 2, 2> state_jacobian_F;
  state_jacobian_F << 1 + this->_delta_t * (this->_angular_vel(1) * tri(1,0) * tri(2,1) - this->_angular_vel(2) * tri(0,0) * tri(2,1)), this->_delta_t * ((this->_angular_vel(1) * tri(0,0)) / pow(tri(1,1), 2) + (this->_angular_vel(2) * tri(1,0)) / pow(tri(1,1), 2)),
                     -1 * this->_delta_t * (this->_angular_vel(1))                                                                    , 1.0 + (-1) * this->_angular_vel(2) * tri(1,1); 
  return state_jacobian_F;
}

Matrix<double, 2, 2> Ekf::_predict_covariance_p(const Matrix<double, 2, 2>& state_jacobian_F)
{
  Matrix<double, 2, 2> pre_covariance_p;
  pre_covariance_p = state_jacobian_F * this->_covariance_p * state_jacobian_F.transpose() + this->_covariance_q;
  return pre_covariance_p;
}

Matrix<double, 2, 1> Ekf::_get_actual_observation_angle()
{
  Matrix<double, 2, 1> observation_angle;
  observation_angle << atan2(this->_linear_acc(1), this->_linear_acc(2)), 
                       -1 * atan2(this->_linear_acc(0), hypot(this->_linear_acc(1), this->_linear_acc(2)));
  return observation_angle;
}

Matrix<double, 2, 2> Ekf::_get_kalman_gain(const Matrix<double, 2, 2>& pre_covariance_p)
{
  Matrix<double, 2, 2> _kalman_gain;
  _kalman_gain = pre_covariance_p * this->_observation_matrix_H.transpose() * (this->_observation_matrix_H * pre_covariance_p * this->_observation_matrix_H.transpose() + this->_covariance_r).inverse();
  return _kalman_gain;
}

void Ekf::_update_covariance_p(const Matrix<double, 2, 2>& kalman_gain, const Matrix<double, 2, 2>& pre_covariance_p)
{
  this->_covariance_p = (Matrix<double, 2, 2>::Identity() - kalman_gain * this->_observation_matrix_H) * pre_covariance_p;
}

geometry_msgs::Vector3 Ekf::_get_corrected_angle(const Matrix<double, 2, 1>& predict_angle,
                                                 const Matrix<double, 2, 1>& actual_observation_angle,
                                                 const Matrix<double, 2, 2>& kalman_gain)
{
  geometry_msgs::Vector3 output;
  this->_roll_pitch = predict_angle + kalman_gain * (actual_observation_angle - predict_angle);
  output.x = this->_roll_pitch(0);
  output.y = this->_roll_pitch(1);
  output.z = this->_yaw;
  return output;
}

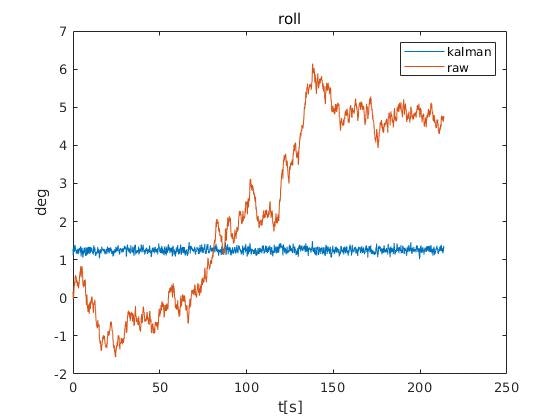
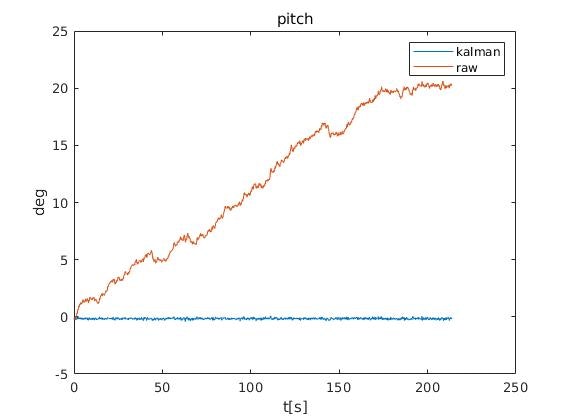
評価

機体を静止させたままで、カルマンフィルタ無しで単純に時間積分したもの(raw)とカルマンフィルタを使用して推定したもの(kalman)を比較したところ、ドリフトが抑えられているようです。

しかしroll角は1°あたりをずっとさまよっているので、バイアスを補正したほうが良いかもしれません。

バイアスの補正はyaw角の時間積分による推定にも使用できるかもしれないので、次回は推定値にジャイロのバイアスを推定する実装を作製してみようと思います。
ここまで読んで頂きありがとうございました。
最新版のコードはgithubにあるのでもしよろしければご覧ください。ミスがありましたら教えていただけますと嬉しいです。

参考

これらのサイトを自分でまとめたり実装を真似したりしました。わかり易すぎて感謝しかないです。

https://www.youtube.com/watch?v=okzVQab36SE
https://qiita.com/Soonki/items/3e9ffb072ba3ba11490e
https://qiita.com/calm0815/items/92021ccea35c28b078e2
https://memo.soarcloud.com/6%E8%BB%B8imu%EF%BD%9E%E6%8B%A1%E5%BC%B5%E3%82%AB%E3%83%AB%E3%83%9E%E3%83%B3%E3%83%95%E3%82%A3%E3%83%AB%E3%82%BF
https://hamachannel.hatenablog.com/entry/2018/05/13/155504
https://myenigma.hatenablog.com/entry/2015/11/09/183738