共分散行列とは？(定義、意味、分布の推定)

「共分散行列」という仰々しい名前から、なんだか堅苦しそうだなと思っていましたが、意味さえ分かってしまえば簡単だったので共有したいと思います。数学的な厳密性については不問としてください。
また、本稿は堀玄先生・平岡和幸先生の「プログラミングのための確率統計(オーム社)」を大いに参考にして書きました。とても分かりやすいので、この手の話で困っている学生は是非手に取ってみてください。

結論から申し上げますと、共分散行列が分かると共分散行列に用いられている乱数の分布が分かるというありがたみがあります。そこで本稿では、「共分散行列から分布のだいたいの形を推定できるようになる」ということを目標にしたいと思います。

#1.定義
$\boldsymbol{X}=(X_1,X_2,...,X_n)$という$X_1$から$X_n$までの確率変数をまとめたベクトルをまず定義しましょう。次に、${\rm V[{\boldsymbol{X}}]}$を$\boldsymbol{X}$の共分散行列だとすると、その定義は以下のようになります。

{\rm V[{\boldsymbol{X}}]}=\left(
\begin{array}{ccc}
 {\rm V}[X_1] & {\rm Cov}[X_1,X_2] & \ldots &  {\rm Cov}[X_1,X_n]\\
 {\rm Cov}[X_2,X_1] & {\rm V}[X_2] & \ldots & {\rm Cov}[X_2,X_n] \\
\vdots & \vdots & \ddots & \vdots \\
{\rm Cov}[X_n,X_1] & {\rm Cov}[X_n,X_2] & \ldots & {\rm V}[X_n]
\end{array}
\right)

${V[X]}$、${{\rm Cov}[X,Y]}$はそれぞれ$X$の分散と$X,Y$の共分散です。定義はどんな教科書にも載っていると思いますので詳しくは参照してほしいと思います。
上式は$\boldsymbol X$がn次元のときの定義ですが、以下ではイメージを捉えやすくするためにn=2としたいと思います。つまり、ここから共分散行列は以下のような形の行列と思ってください。

{\rm V[{\boldsymbol{X}}]}=\left(
\begin{array}{ccc}
 {\rm V}[X_1] & {\rm Cov}[X_1,X_2] \\
{\rm Cov}[X_2,X_1] & {\rm V}[X_2]
\end{array}
\right)

#2.意味
本稿ではあくまでイメージをざっくりと説明していくので
${V[X]}$：$X$の分布の広がり
${{\rm Cov}[X,Y]}$：$X,Y$の一致度
という程度にイメージを持っておくといいと思います。

一度具体例をみてみましょう。たとえば

という分布があるとすると、その共分散行列はCPU計算の結果

{\rm V[{\boldsymbol{X}}]}=\left(
\begin{array}{ccc}
 0.88 & -0.25 \\
-0.25 & 8.15
\end{array}
\right)

となるそうです。対角項は非対角項に比べて大きく、さらに(2,2)成分(=8.15)は(1,1)成分(=0.88)よりもかなり大きい値であることがわかります。

後出しになりますが、$X_1$は平均0,分散1の正規分布に従う乱数であり、$X_2$は$X_1$とは独立な平均0,分散9の正規分布に従う乱数としてシミュレーションを実行しました。これは100個の点でシミュレーションをしているのですが、次は10000個の点を生成して同じようにシミュレーションをしてみます。

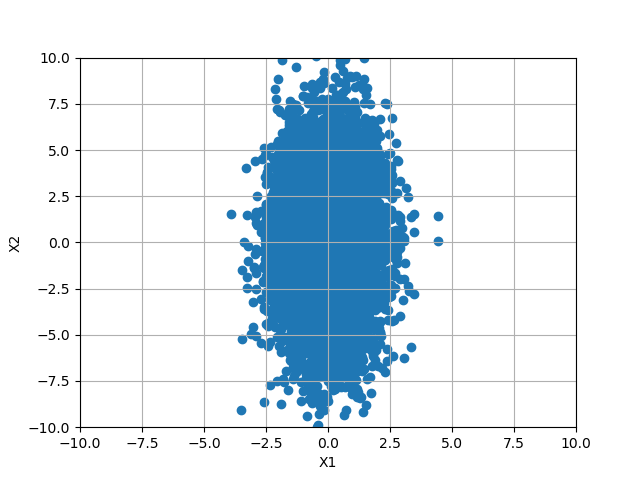
この場合の共分散行列は、計算によると

{\rm V[{\boldsymbol{X}}]}=\left(
\begin{array}{ccc}
 1.00 & 0.03 \\
 0.03 & 9.15
\end{array}
\right)

どうでしょう、だんだん共分散行列の意味が分かってきたのではないでしょうか。
生成する乱数の数を大きくしていくと、対角項は各次元の乱数の分散に、非対角項はその一致度に収束していきます。
上の例の場合では、(1,1)成分は$X_1$の分散である1に、(2,2)成分は$X_2$の分散である9に収束します。また、$X_1$と$X_2$は独立であるので、その一致度は0に収束していきます。
「なんだ、そんなもんかよ。ただ単純に分散を計算するだけならわざわざ行列にしなくてもいいじゃん」とこの段階では思うかもしれませんが、共分散行列という形にすることによる威力が発揮されるのは次のような場合です。

#3.分布の推定
たとえば

{\rm V[{\boldsymbol{X}}]}=\left(
\begin{array}{ccc}
 5 & 4 \\
 4 & 5
\end{array}
\right)

という共分散行列から、$X_1,X_2$の2次元正規分布を推定しなければならない場合、どのようにしたら良いでしょうか。
2章で述べたパターンでは各次元の乱数に相関が無かったので簡単に分布の形を知ることができましたが、今回は非対角項に値があるのでどうやら$X_1$と$X_2$の間には何らかの相関があるようです。では、具体的な分布を推定するためにはどのような手続きを踏めばよいのでしょうか。
そのためにまずは、${\rm V[{\boldsymbol{X}}]}$の固有値と固有ベクトルを求めてみましょう。すなわち、以下のような等式を満たす$\lambda$と$\boldsymbol r$を求めます。

{\rm V[{\boldsymbol{X}}]}{\boldsymbol r} = {\lambda}{\boldsymbol r}

固有値・固有ベクトル求め方や意味に関しては本筋から離れてしまうので、本稿では略すことにします。(また別の記事で書きます)
上記の例の場合、${\lambda}=1,9$でその時の$\boldsymbol r$はそれぞれ一例として$[1,-1]^{\rm T},[1,1]^{\rm T}$があります。
少しズルいですが、先に$X_1,X_2$の分布をカンニングしましょう。

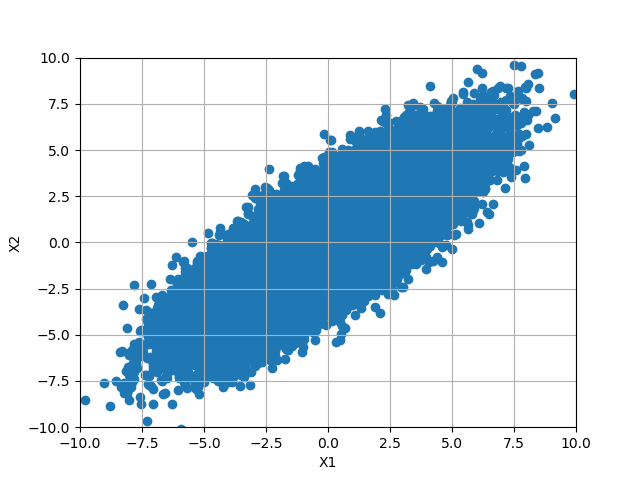
カンニングした結果と固有値、固有ベクトルをジッと眺めているとなにか見えてくることはないでしょうか。そう、
${\lambda}=1$は短軸方向の広がり、$[1,-1]^{\rm T}$は短軸方向を示すベクトル、
${\lambda}=9$は長軸方向の広がり、$[1,1]^{\rm T}$は長軸方向を示すベクトルを表していますね。
このように、「共分散行列の固有値・固有ベクトルを求めることで分布の大体の様子が分かる」ということがわざわざ乱数を共分散行列という形にまとめることの意義です。

#4.まとめ
1章では共分散行列の定義から紹介し、2章では2次元正規分布に従い乱数を生成しシミュレーションにより共分散行列を計算しました。ここで、対角項には各次元の乱数の値の広がりが表れて、さらにもし各次元の乱数が独立だった場合には非対角項は0に収束することを示しました。
3章では本稿の目標を達成するために、一般的な形の共分散行列から大体の分布を推定する方法について説明しました。

#5.コード
クソコードですが貼っておきます。$X_1,X_2$の分散や平均を変えてみたり、分布の回転角(theta)を変えてみたりすることでたしかに共分散行列の固有値・固有ベクトルが$\boldsymbol X$の分布を表していることを実感してもらえると思います。

import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt

#データ数　上げると精度が上がる
N = 10 ** 5

#乱数の生成
x1 = np.random.normal(0, 1, N)
x2 = np.random.normal(0, 3, N)

#二つの乱数列の結合　それぞれ異なるパラメータを設定したいため後から結合する
x = np.vstack([x1, x2])

#回転前の分布の表示　この時点ではx軸方向かy軸方向へ平べったい楕円形
#plt.scatter(x[0][:], x[1][:])

#xの分布の回転　これによって一般系の2次元正規分布に変形
theta = np.pi / 4
rot = np.array([[np.cos(theta), np.sin(theta)], [-np.sin(theta), np.cos(theta)]], np.float32)
x = np.dot(rot, x)
plt.scatter(x[0][:], x[1][:])
plt.grid()
plt.xlabel('X1')
plt.ylabel('X2')
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.show()

#共分散行列の計算
V_x1 = np.dot(x[0][:].T, x[0][:]) / N - (np.sum(x[0][:]) / N)**2
Cov_x1x2 = np.dot(x[1][:].T, x[0][:]) / N - (np.sum(x[1][:]) / N)*(np.sum(x[0][:]) / N)
Cov_x2x1 = np.dot(x[0][:].T, x[1][:]) / N - (np.sum(x[0][:]) / N)*(np.sum(x[1][:]) / N)
V_x2 = np.dot(x[1][:].T, x[1][:]) / N - (np.sum(x[1][:]) / N)**2
V_X = np.array([[V_x1, Cov_x1x2], [Cov_x2x1, V_x2]], np.float32)

#共分散行列の固有値と固有ベクトルの表示
eigenvector = LA.eig(V_X)
print(V_X)
print(eigenvector)