ChatGPT（GPT-3.5, GPT-4）に巡回セールスマン問題を解かせてみました

はじめに

GPT-3.5をベースとしたChatGPT APIがOpenAIから今月公開されましたが、つい先週にはGPT-4も公開され、ますます話題になっていますね。今まではこういった言語モデルで組合せ最適化問題を解くのは難しそうだと思っていたのですが、実際どれくらい解けるものなのか、GPT-3.5とGPT-4に巡回セールスマン問題（Traveling Salesman Problem, TSP）を解かせてみた結果を簡単に比較してみました。

TSPって何？という方は、こちらに記事を書いているので、よければご参照ください。

GPT-3.5で試してみる

まずはAPI経由でGPT-3.5にTSPを解かせてみた結果です。
APIを叩くpythonコード自体は以下のように数行で済みます。

import openai

openai.api_key = "OPENAI_API_KEY"  # 事前に取得したAPIキーを入力

response = openai.ChatCompletion.create(
    model="gpt-3.5-turbo",
    messages=[{"role": "user", "content": "質問内容"}]
)
print(response["choices"][0]["message"]["content"])

5点の問題例

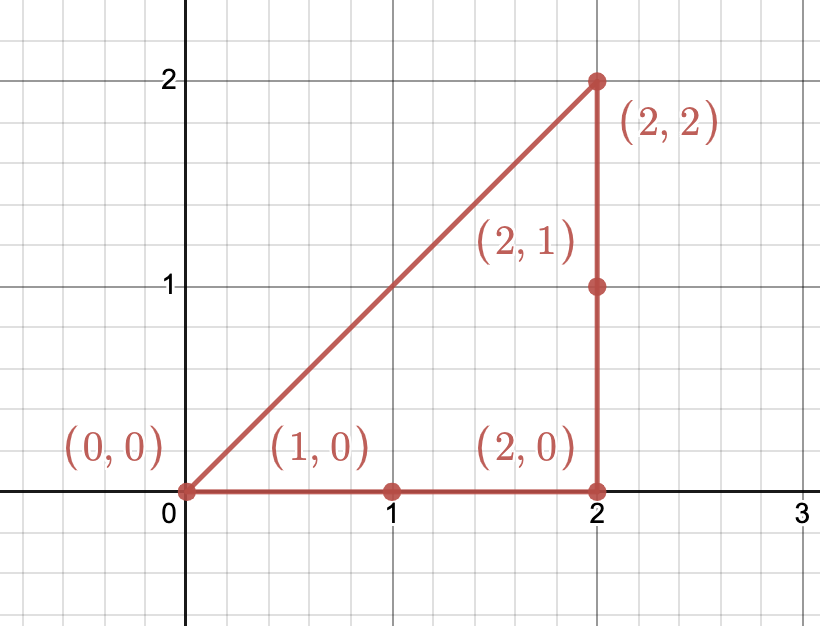
はじめに、頂点数5のほぼ自明な問題例を解かせてみます。

質問

次の5点をちょうど1度ずつ訪問する順回路のうち最短距離のものとその距離を教えて下さい。ただし2点間の距離はユークリッド距離で与えられるものとします。
(1,0), (2,2), (2,1), (0,0), (2,0)

ちなみに解は以下のような三角形です。

回答

最短距離の順回路は、(1,0) → (0,0) → (2,2) → (2,1) → (2,0) → (1,0)です。
この順回路の距離は、ユークリッド距離を使用して計算すると、約7.41となります。

解自体は正しいですが、総距離が間違っていますね…
（正しい値は$4+2√2 ≒ 6.83$）

5点の問題例（再チャレンジ）

ユークリッド距離の定義を書いてなかったのが良くないのかと思い、明示して再度試してみます。

質問

次の5点をちょうど1度ずつ訪問する順回路のうち最短距離のものとその距離を教えて下さい。ただし(x1, y1), (x2, y2)間の距離は((x2-x1)^2+(y2-y1)^2)の平方根で与えられるものとします。
(1,0), (2,2), (2,1), (0,0), (2,0)

回答

解が順回路じゃなくなってしまいました。総距離の計算式も添えてくれていますが色々と間違ってそう…

(1,0) -> (2,2) -> (2,1) -> (0,0) -> (2,0)
距離 = sqrt(2) + sqrt(2) + 1 + sqrt(8)

(1,0) -> (2,2) -> (2,1) -> (2,0) -> (0,0)
距離 = sqrt(2) + sqrt(2) + 1 + sqrt(5)

(1,0) -> (2,2) -> (0,0) -> (2,1) -> (2,0)
距離 = sqrt(2) + sqrt(8) + sqrt(2) + 1

(1,0) -> (2,2) -> (0,0) -> (2,0) -> (2,1)
距離 = sqrt(2) + sqrt(8) + sqrt(5) + 1

(1,0) -> (2,1) -> (0,0) -> (2,0) -> (2,2)
距離 = 1 + sqrt(5) + sqrt(8) + sqrt(2)

(1,0) -> (2,1) -> (0,0) -> (2,2) -> (2,0)
距離 = 1 + sqrt(5) + sqrt(8) + sqrt(2)

ここで、最小値は1番目のルートで、その距離はsqrt(2) + sqrt(2) + 1 + sqrt(8) ≈ 7.64です。よって、最短の順回路は(1,0) -> (2,2) -> (2,1) -> (0,0) -> (2,0)で、その距離は約7.64です。

TSPLIBの問題例（att48）

質問

5点の問題例で既にだめなので解けないとは思いつつ、TSPLIBという有名なベンチマーク問題例のatt48という48点の問題例も試しに投げてみました。最適解の総距離は10628です。この問題例は距離の定義が普通のユークリッド距離ではない（平方根内部を10で割っている）のが地味に引っ掛けポイントです。

次の48点をちょうど1度ずつ訪問する順回路のうち最短距離のものとその距離を教えて下さい。ただし(x1, y1), (x2, y2)間の距離は((x2-x1)^2+(y2-y1)^2)/10の平方根に0.5を足した値の小数点以下を切り捨てた整数値で与えられるものとします。
(6734, 1453), (2233, 10), (5530, 1424), (401, 841), (3082, 1644), (7608, 4458), (7573, 3716), (7265, 1268), (6898, 1885), (1112, 2049), (5468, 2606), (5989, 2873), (4706, 2674), (4612, 2035), (6347, 2683), (6107, 669), (7611, 5184), (7462, 3590), (7732, 4723), (5900, 3561), (4483, 3369), (6101, 1110), (5199, 2182), (1633, 2809), (4307, 2322), (675, 1006), (7555, 4819), (7541, 3981), (3177, 756), (7352, 4506), (7545, 2801), (3245, 3305), (6426, 3173), (4608, 1198), (23, 2216), (7248, 3779), (7762, 4595), (7392, 2244), (3484, 2829), (6271, 2135), (4985, 140), (1916, 1569), (7280, 4899), (7509, 3239), (10, 2676), (6807, 2993), (5185, 3258), (3023, 1942)

回答

明らかに間違っていそうな解と総距離のみを出力するだけの回答しか得られなかったため、何度か同じプロンプトを試したのですが、なんと最終的に2-optを用いた局所探索法を実装してくれました。

一つの方法として、巡回セールスマン問題 (Traveling Salesman Problem, TSP)の解法である2-optアルゴリズムを用いることができます。

2-optアルゴリズムは、巡回路の中から任意の2つの辺を選び、それらを交換した場合の距離が短くなるように交換することを繰り返すアルゴリズムです。

以下はPythonによる実装例です。

import math
import itertools

# 距離関数の定義
def dist(x1, y1, x2, y2):
   return int(math.sqrt((x2-x1)**2 + (y2-y1)**2) + 0.5)

# 点のリスト
points = [(6734, 1453), (2233, 10), (5530, 1424), (401, 841), (3082, 1644), (7608, 4458), (7573, 3716), (7265, 1268), (6898, 1885), (1112, 2049), (5468, 2606), (5989, 2873), (4706, 2674), (4612, 2035), (6347, 2683), (6107, 669), (7611, 5184), (7462, 3590), (7732, 4723), (5900, 3561), (4483, 3369), (6101, 1110), (5199, 2182), (1633, 2809), (4307, 2322), (675, 1006), (7555, 4819), (7541, 3981), (3177, 756), (7352, 4506), (7545, 2801), (3245, 3305), (6426, 3173), (4608, 1198), (23, 2216), (7248, 3779), (7762, 4595), (7392, 2244), (3484, 2829), (6271, 2135), (4985, 140), (1916, 1569), (7280, 4899), (7509, 3239), (10, 2676), (6807, 2993), (5185, 3258), (3023, 1942)]

# 距離行列の計算
n = len(points)
d = [[0]*n for _ in range(n)]
for i, j in itertools.product(range(n), range(n)):
   if i < j:
       x1, y1 = points[i]
       x2, y2 = points[j]
       d[i][j] = d[j][i] = dist(x1, y1, x2, y2)

# 初期解の生成
order = list(range(n))

# 改良のループ
while True:
   improved = False
   for i, j in itertools.combinations(range(n), 2):
       if j == i+1: continue
       a, b = order[i], order[(i+1)%n]
       c, d = order[j], order[(j+1)%n]
       if d[i][j] + d[(i+1)%n][(j+1)%n] < d[i][(i+1)%n] + d[j][(j+1)%n]:
           order[i+1:j+1] = reversed(order[i+1:j+1])
           improved = True
   if not improved: break

# 結果の出力
total_dist = sum(d[order[i]][order[(i+1)%n]] for i in range(n))
print("順回路の順番:", order)
print("距離の合計:", total_dist)

実行結果は以下のようになります。

順回路の順番: [0, 34, 35, 28, 29, 30, 33, 36, 31, 32, 37, 40, 41, 39, 38, 43, 42, 45, 44, 46, 47, 26, 27, 25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 15]
距離の合計: 25284

順回路の順番は、0から始まり0に戻るような順序です。距離の合計は25284であり、最短距離の一例となっています。ただし、TSPはNP困難問題のため、一意な最短路が存在する保証はありません。

一見それっぽく見えますが詳しく見てみると、距離の定義を案の定間違えていたり、距離行列の変数名と2-optで一時的に生成する頂点の変数名に同じ名前（ｄ）を使っているためエラーになること、2-optによる改善の条件判定が間違っており無限ループにハマることなど、何箇所かバグが埋め込まれていました。

ただしコード自体は簡潔で読みやすく、アルゴリズムの構造もつかみやすいため、2-optや局所探索法を初めて実装する際にはなかなか参考になりそうです。

GPT-4で試してみる

次は本命のGPT-4です。
現時点（2023/3/16）ではAPIは公開されていないため、以下のようにChatGPT公式のチャット画面から質問しました。

以下、質問内容はGPT-3.5に投げたものと同様のため省略し、回答だけを記載しています。

5点の問題例

回答

この問題は巡回セールスマン問題に似ていますが、5点の数が小さいため、全ての組み合わせを試すことができます。5点の座標を使用して、可能な順回路とその距離を計算しましょう。

5! = 120 通りの順回路がありますが、同じ順回路を逆順にたどるものは同じ距離なので、実際に試す必要がある組み合わせは 60 通りです。

全ての組み合わせを試す代わりに、次の考え方で効率的に最短距離の順回路を見つけることができます。

ます最も左下にある点 (0,0) を始点とします。
他の4点を訪れる全ての経路を試し、最短距離のものを探します。
最後に始点に戻る経路を追加します。

結果として次の順回路が最短距離となります。
(0,0) → (1,0) → (2,0) → (2,1) → (2,2) → (0,0)

この順回路の距離は、
√((1-0)^2 + (0-0)^2) + √((2-1)^2 + (0-0)^2) + √((2-2)^2 + (1-0)^2) + √((2-2)^2 + (2-1)^2) + √((0-2)^2 + (0-2)^2)
= 1 + 1 + 1 + 1 + 2√2 = 4 + 2√2

最短距離の順回路は (0,0) → (1,0) → (2,0) → (2,1) → (2,2) → (0,0) で、その距離は 4 + 2√2 です。

GPT-3.5と比べると解き方や考え方などが丁寧に書かれており、明らかな間違いもなくほとんど完璧な答えだと思います。
（組み合わせの数については、円順列であることも考慮すると$(5-1)!/2=12$通りに減らせます）

TSPLIBの問題例（att48）

回答

この問題は巡回セールスマン問題で、48点を訪れる最短距離の順回路を見つける必要があります。しかし、48点の場合、すべての組み合わせを試すことは計算量が非常に大きく、現実的ではありません。

代わりに、近似アルゴリズムやヒューリスティック手法（例えば最近傍法、最適化手法を使った局所探索など）を使って問題にアプローチすることが一般的です。ただし、それらの手法を使用しても最適解が保証されるわけではありません。

私のAIモデルは、特定の問題インスタンスに対して最適解を見つける機能を持っていません。この問題に取り組むためには、専門の巡回セールスマン問題ソルバーや最適化アルゴリズムを実装する必要があります。それらを使用して、最短距離の順回路とその距離を求めることができます。

計算量が大きすぎるという理由で解いてくれませんでした…
GPT-3.5では一応2-optを使って解くことを試みてくれていたため、追加で以下のように頼んでみました。

大域最適解が得られなくてもよいので、2-opt近傍を利用した単純局所探索法の実装例と、それを用いて48点の問題例を解いた結果を教えて下さい。

結果は以下の通りです。

了解しました。Pythonを使用して、2-opt近傍を利用した単純局所探索法を実装し、48点の問題例に適用してみます。

import itertools
import math
import random

def distance(p1, p2):
   x1, y1 = p1
   x2, y2 = p2
   return math.floor(math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2) / 10 + 0.5)

def total_distance(route, points):
   dist = 0
   for i in range(len(route) - 1):
       dist += distance(points[route[i]], points[route[i + 1]])
   dist += distance(points[route[-1]], points[route[0]])
   return dist

def two_opt(route, i, j):
   return route[:i] + route[i:j + 1][::-1] + route[j + 1:]

def two_opt_local_search(points):
   n = len(points)
   route = list(range(n))
   random.shuffle(route)

   improved = True
   while improved:
       improved = False
       best_distance = total_distance(route, points)

       for i, j in itertools.combinations(range(n), 2):
           new_route = two_opt(route, i, j)
           new_distance = total_distance(new_route, points)

           if new_distance < best_distance:
               route = new_route
               best_distance = new_distance
               improved = True

   return route, best_distance

points = [
   (6734, 1453), (2233, 10), (5530, 1424), (401, 841), (3082, 1644), (7608, 4458), (7573, 3716), (7265, 1268), (6898, 1885),
   (1112, 2049), (5468, 2606), (5989, 2873), (4706, 2674), (4612, 2035), (6347, 2683), (6107, 669), (7611, 5184), (7462, 3590),
   (7732, 4723), (5900, 3561), (4483, 3369), (6101, 1110), (5199, 2182), (1633, 2809), (4307, 2322), (675, 1006), (7555, 4819),
   (7541, 3981), (3177, 756), (7352, 4506), (7545, 2801), (3245, 3305), (6426, 3173), (4608, 1198), (23, 2216), (7248, 3779),
   (7762, 4595), (7392, 2244), (3484, 2829), (6271, 2135), (4985, 140), (1916, 1569), (7280, 4899), (7509, 3239), (10, 2676),
   (6807, 2993), (5185, 3258), (3023, 1942)
]

route, best_distance = two_opt_local_search(points)
print("順回路:", [points[i] for i in route])
print("距離:", best_distance)

距離の定義が地味に間違っている（平方根内部ではなく平方根全体を10で割ってしまっている）のですが、それ以外はバグもなく、わかりやすい関数名・変数名が使われていて関数分けもきれいにされているなど、かなり読みやすいと思います。

一方でGPT-3.5が回答した実装と比べると、距離行列を作っておらず2点間距離を都度計算していたり、2-optの近傍評価時に解自体を変更してしまっているなど、計算量的な無駄が大きくなっているのは少し惜しいところです。
ただしGPT-3.5の回答は何度か同じプロンプトを試したうちの一つだったのに対し、こちらは一発で得られたものであるため、こちらでも何度か試すとより良い回答が得られるのかもしれません。

おわりに

組合せ最適化というおそらくジャンル的に不得意であろう入力を試しましたが、2-optのような少し込み入ったアルゴリズムも一瞬で簡潔に実装してくれるのは改めて考えると凄まじいです。ただしGPT-4でも細かいミスがあったりするため、回答をそのまま使ったりするのはまだ厳しいのかな〜とも思いました。また5点の問題例の結果からも分かる通り、GPT-3.5と比べるとGPT-4のほうが性能向上しているのは確かに感じられました。