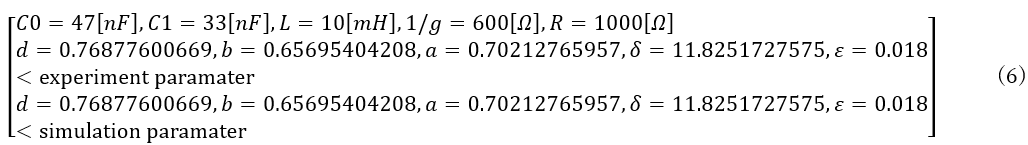●はじめに
こんにちは。ビットキーでエンジニアとして働いている平瀬です。
普段は、ハードウェア開発や電子回路設計を中心に、自社製品の仕様検討から試作、評価まで幅広く携わっています。新しい部品の選定や回路の最適化、実機評価など、ものづくりならではの試行錯誤を楽しみながら日々業務に取り組んでいます。
本投稿では、プライベートで試している技術や、個人的に注目しているツール・開発手法などを気軽に紹介していきたいなと思います。
仕事とは少し違った視点での技術探求や、小さな発見が誰かの役に立てば嬉しいです。
今回取り上げるテーマは、電子回路で見るChaos(カオス)です。
はて???と思われる方もたくさんいらっしゃるかと思いますが、カオスは相対性理論や量子力学とともに20世紀3大発見の一つと言われている極めて重要な概念と言われ、一時期だいぶ盛り上がりを見せた現象です。
そんなカオスではありますが、カオスとは何かを説明するにはとてもとても難しい言葉を沢山並べないと説明ができませんので、別の機会があれば説明するものとして今回はエレキエンジニアならでは(?)の視点でもってカオスを紹介したいと思います。
※カオスとは何かを本で見たい方いたら(いるのか?)、おすすめしたい本がこちら。
カオス: カオス理論の基礎と応用 (Information&Computing 49) 合原 一幸
カオスと言えば合原先生。知らない人は居ないんじゃないかな?というぐらい有名な人の本です。
私の書庫にも並んでおります。
●電子回路で表現するカオスの世界
本題に入ると、そんなカオスを電子回路で表現するのが今回の肝になります。
あーだこーだと理論を並べたいところではありますが、電子回路で表現したカオスとはどのようなものか、先に結果をお見せします。

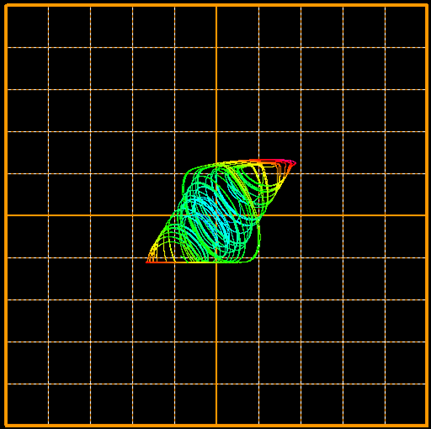
図1.アナログオシロスコープで見るカオス図形コレクション抜粋
何枚か貼りました。これは、電子回路で表現したカオス発振させた様子です。
この様子は電圧信号と時間との関係を視覚化するためのツールとして昔から電子回路エンジニアが使っているオシロスコープという測定器を使用しておりまして、そのオシロスコープの機能にあるリサージュ図形表示機能で描画したカオスになります。
どうでしょう?不思議な図形に見えませんか?
私が電子回路でカオスを表現したいなぁと思ったのはこの図形がとてもとても不思議で綺麗だなぁ~と感じたことから始まっています。
※リサージュ図形と聞くと工学とか音楽あたりを学んだ経歴がある方は馴染みあると思いますが、他分野のかただと頭に?マークがつく方もいらっしゃると思います。リサージュ図形はざっくりいうと、2つの信号を合成した軌跡を画面上に表示し、視覚的に確認する方法で工学の他、音楽でも使われている図形です。カオスを表示すると通常の正弦波のような発振波形では想像できない複雑な図形になります。詳しくはインターネットで、「リサージュ図形とは」のようなワードで調べてみてください。どんなところで使われるのか、通常どんな図形になるのかがわかると思います。インターネット上で検索できるリサージュ図形には上図であげたカオスのような図形は見つからず(多分)、いかにカオスが摩訶不思議な形なのかがわかるかなと思います。
●カオス発振回路
さてさて、実は既に一番の目的は達成してしまいました。
私が今回投稿してみようかなと思ったのは、“電子回路で表現したカオスの世界がどんな感じに見えるのかを、見てもらいたい”だからです。前の項で、カオスのリサージュ図形を見ていただけたので、もう満足。お腹いっぱいです。ごちそうさま。
ここから先は、カオス発振回路の話と何をもってカオスと呼ぶかなどの理論武装になってしまうので、お堅いお話になります。そのため、興味がある人だけゆっくりスクロールしていただき、それ以外の方はそっと閉じるか終わりまで飛びましょう!
では、早速実際のカオス発振回路を見ていきます。
★重要なのは、カオス発振回路を実験で再現しました!これはこれで良いのですが、理論的にも再現できることが重要です。そこで、無料で誰もが使えるLTspiceという回路シミュレータを使って再現してみます。
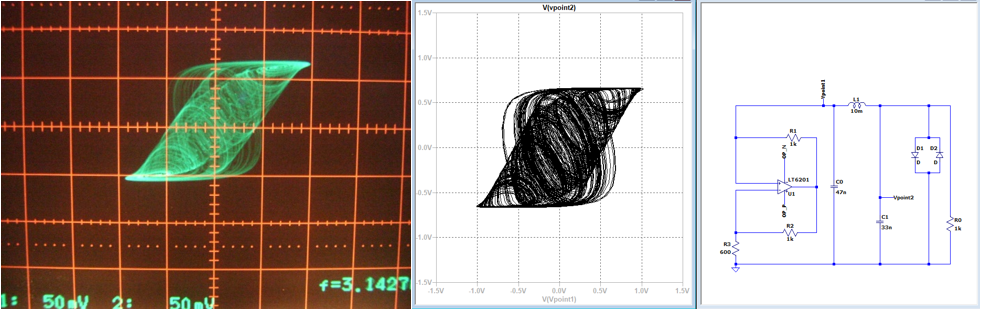
結果が、図2です。
図2.実験とシミュレーションによるカオス
(左から順に実験図、シミュレーション図、回路図)
見ていただくとわかるように、実験で得られた図とシミュレーションで得られた図がほぼ同じになっていますね。
これは、実験で得られた結果を理論でもって証明できることになります。
LTspiceのアルゴリズム詳細は明かされてはいませんが、spiceの名を冠しているので中身の核はニュートン法と呼ばれる手法になっています。
ざっくり言うと、回路のネット情報から非線形方程式を組んで、これを数値積分とニュートン法によって解くのがspiceです。このあたりの原理は色々な情報が転がっていると思いますので興味がある方は探してみてください。
というわけで、spiceと同じようなこと=方程式作って、数値積分してニュートン法で解く!ことをしてみました。
図3.spiceを真似た数値解析の結果
実験図やspiceシミュレーションに近い図形になっていると思います。
こちらの図はCでコード書いて得られた結果です。
図形を表示する枠はオシロスコープっぽくしてみました(笑)
波形が色付けされていますが、これは数値解析によって得られたノルム量を色で表したもので、具体的にはノルムの最小値を青,最大値をマゼンタとし,256階調で表示しています。大まかな色の流れとしては青→シアン→緑→黄→赤→マゼンタの順にノルムの量が大きくなります。ノルムはベクトル空間における距離のことですが、ここで言うノルムは言い方をかえると、1回のステップでの変化量です。つまり、青いところはあまり変化しないところ、赤いところは大きく変化するところになります。
ノルムの色付けは一応、変化量の観測をするためなのですが、何故そんなことをしたのか細かく言うのはここではおいておきます。
ここで一番大事なことは、とりあえず、spiceと同じようなことは自分で方程式立てて数値解析すれば誰でも再現できるよとなるわけで、それはつまり、実験はspice使わなくても自力で再現できるということです。
次の項目では実際組み立てた方程式と実際のパラメータを紹介したいと思います。
●カオス発振器の回路方程式
図4.カオス発振回路の部品番号設定
-gは負性抵抗です。回路図のオペアンプで組んだところですね。
ここで、非線形素子のダイオード対を図5のように区分線形化して定義します。

図5.ダイオードの区分線形化
すると、次の無次元化方程式となります。図5のように区切ると3パターン生まれます。

このように3つの線形な微分方程式で表すことができます。
ダイオードを区分線形化したのは、回路方程式を解く上で単純にしたいことと、3組分けることでそれぞれの組の領域での固有値と固有空間から挙動を説明しやすくするためです。
無次元化したのは次元量を無くして、方程式を簡単にするためです。
ちょっとだけ補足です。
固有値は別の言い方をすると特性値になります。
固有値は固有方程式の解を指すのですが、分野によっては固有方程式を特性方程式と呼び、特性方程式の解を特性値と呼ぶことがあります。
また、次元という言い方をしていますが、物理学における言葉です。今回の回路においては、3次元になるのですが、ものすごく簡単に言うと、コンデンサとコイルの数の総数が次元数になります。回路ではコンデンサ2個、コイルが1個になっていますね。なので、3次元。これら3個の素子は時間の概念を持つ素子なので次元扱いに。ちなみに抵抗は物理学的な次元を持たないので次元数にはカウントしません。
あとは単純に方程式を解いて、固有値を求めます。
式(3)~(5)に相当する固有値を求めた結果が以下です。

●カオス的であることを何を持って証明するか
カオス的であるという方法にはいくつか方法がありまして、その一つにリアプノフ指数というものがあります。
初期値がほんのわずかに異なる二つの軌道がどのくらいの速さで離れていくかをあらわす指標です。カオスの場合、この指数値が正であることが条件になっていますので、計算してみて正の値になればカオス的と判断できます。
リアプノフ指数とカオスをキーワードに検索するとたくさん説明や文献出てきますので細かい計算方法についてはそちらにお任せして、結果だけを書きますね。
と計算できます。これの最大リアプノフ指数が正となるとカオス的となりますので、今回の結果では最大リアプノフ指数が正となり、カオス的と言えます。
尚、数値解析では収束しているかの確認が重要なので、収束性を確認しています。

図6.リアプノフ指数λ1の収束の様子
●終わりに
本投稿は論文ではなく筆者が趣味で行っている内容を気軽に書いているため、電子回路で見るカオスの紹介と今回の回路がカオスであることを表す手法をざっくりとご紹介しました。
カオスは本当に奥がとても深く、何をもってカオスと言うのかに対して様々な数学的なアプローチが成されます。
どれも興味を引くような美しい数式や図形の数々。学びを得るのにとても楽しい分野です。そして、電子回路で見るカオスはとても不思議な波形で見た目がとても楽しい。実験をしているとついつい目を奪われて時間を忘れてしまいます。
全ての人に刺さるようなメジャーで煌びやかなものではありませんが、とてもとてもマニアックできっとどこかの誰かの心をくすぐるようなそんな現象がカオスだと私は思っています。
もし、カオスに興味が湧いた方がいらっしゃいましたら是非、電子回路(シミュレーションでもOK)でのカオス体験にチャレンジしてみてください。