お絵かきロジックを誰でも理解できるシンプルな背理法だけで解くアルゴリズム（お試しも出来ます）

はじめに

お絵かきロジック（ののぐらむ、イラストロジック）は、数字のヒントを元にマスを塗りつぶして絵を完成させるパズルです。この記事では、シンプルな背理法を使ってお絵かきロジックを解くアルゴリズムを紹介します。

背理法とは

ある仮定をおいて矛盾すれば仮定が誤りであると確定する手法
つまりお絵かきロジックの解法においては
・黒マスと仮定し、矛盾すれば白マスと確定
・白マスと仮定し、矛盾すれば黒マスと確定
する方法です

お絵かきロジックを解くプログラム

まずは、実際にランダムに作ったパズルをコンピューターが解く様子を体験してみてください

起動時および「再作成」ボタンでランダムに問題を作成します
「クリア」→「解析実行」で問題を解きます

もっと詳しい操作方法はこちらのREADMEを参照ください
※フレーム数でアニメーションのスピードを調整することが出来ます
　詳しくはこちらの記事を参照ください
　

アルゴリズム

まず要となる２つの関数を紹介します

leftAlignLineCells関数

// 定数定義
const BLACK = 1;
const WHITE = 2;
const UNKNOWN = 0;

/**
 * いずれかの1行または1列について、対応するヒントに基づき
 * ブロックを出来る限り左揃えにした配列を取得する
 * @param lineHints 行または列のヒントを格納した配列	例：[1,2,1]
 * @param lineCells 現在のブロック状態（白,黒,未）を格納した配列	例：[未,未,未,未,黒,未,白,未]
 * @returns 左揃えのブロック状態（白,黒,未）を格納した配列、エラー時はnull	例：[黒,白,白,黒,黒,白,白,黒]
 */
function leftAlignLineCells(lineHints: number[], lineCells: number[]): number[] | null {
  const blockCount = lineHints.length;
  const cellCount = lineCells.length;

  // 最も右端の黒マスの位置を保存（存在しない場合は-1を設定）
  const maxRightPos = lineCells.lastIndexOf(BLACK);

  // 各ブロックの右端と左端の位置を格納する配列を定義
  const rightPos: number[] = new Array(blockCount);
  const leftPos: number[] = new Array(blockCount);

  let k = 0;
  rightPos[k] = lineHints[k] - 1;

  outer: while (true) {
    // 最後(最も右端)のブロックの時
    if (k === blockCount - 1) {
      // もっと右に黒マスがあればその位置まで右側にシフト
      if (rightPos[k] < maxRightPos) {
        rightPos[k] = maxRightPos;
      }
    }

    // カレントブロックの左端を設定
    leftPos[k] = rightPos[k] - lineHints[k] + 1;

    // カレントブロック内を右端から左端に向かって1文字ずつ照合
    for (let i = rightPos[k]; i >= leftPos[k]; i--) {
      if (lineCells[i] === WHITE) {
        // 白マスの右にカレントブロック全体をシフト
        rightPos[k] = i + lineHints[k];
        if (rightPos[k] >= cellCount) return null;// ブロックの右端がはみ出た
        // カレントブロックをやり直し
        continue outer; // 外側のループを続ける
      }
    }

    // カレントブロックの左隣のマスから左側のブロックまで1文字ずつ照合
    const tmp = k > 0 ? rightPos[k - 1] + 1 : 0;
    for (let i = leftPos[k] - 1; i >= tmp; i--) {
      if (lineCells[i] === BLACK) {
        if (k === 0) return null; // 先頭(最も左端)ブロックのさらに左に黒マスあり
        // 左側のブロックの右端を黒マスの位置まで右側にシフト
        rightPos[k - 1] = i;
        // 1つ前(左)のブロックをやり直し
        k--;
        continue outer; // 外側のループを続ける
      }
    }

    // 次のブロックへ進む
    k++;
    if (k >= blockCount) break;

    rightPos[k] = rightPos[k - 1] + 1 + lineHints[k];
    if (rightPos[k] >= cellCount) return null;
  }

  // 結果の配列を作成（すべて白で初期化）
  const result: number[] = new Array(lineCells.length).fill(WHITE);
  for (let i = 0; i < blockCount; i++) {
    // leftPos[i]～rightPos[i]までの範囲を黒で埋める
    result.fill(BLACK, leftPos[i], rightPos[i] + 1);
  }
  return result;
}

特定の行または列に対して、ヒントと現在のブロック状態に基づいて、出来るだけ左寄せの状態を作ります

fixLineCells関数

/**
 * いずれかの1行または1列について、ヒントと現在のブロック状態に基づいて、
 * 確定可能なマスを全て確定する
 * 引数:
 * @param lineHints 行または列のヒントを格納した配列 	例：[2,2]
 * @param lineCells 現在のブロック状態（白,黒,未）を格納した配列  例：[未,未,白,未,未,未]
 * @returns Tuple
 * - number: 確定したマスの数、エラー時は-1
 * - number[]: 確定可能なマスを全て確定した後の配列  例：[黒,黒,白,未,黒,未]
 */
function fixLineCells(lineHints: number[], lineCells: number[]): [number, number[]] {
  // ブロックを左寄せする
  const leftAligned = leftAlignLineCells(lineHints, lineCells);
  if (leftAligned === null) return [-1, []];

  const result = Array.from(lineCells);
  const testLineCells = Array.from(lineCells);
  let count = 0;

  for (let i = 0; i < lineCells.length; i++) {
    if (testLineCells[i] === UNKNOWN) {
      testLineCells[i] = leftAligned[i] == BLACK ? WHITE : BLACK;
      if (leftAlignLineCells(lineHints, testLineCells) === null) {
        // 矛盾すれば仮定と反対の色で確定
        result[i] = leftAligned[i];
        count++;
      }
      // 元に戻す
      testLineCells[i] = UNKNOWN;
    }
  }
  return [count, result];
}

特定の行または列に対して、leftAlignLineCells関数を実行し、
その結果を使って左端のマスから順番に背理法を実行し、確定できるマスをすべて確定させます

背理法の実行方法は
leftAlignLineCells関数の実行結果が
黒になったマスについては、いったん白マスに確定させてからleftAlignLineCells関数を実行し、エラーになったら黒マスで確定します
白になったマスについては、その反対のことを実行します
※leftAlignLineCells関数の結果が黒のマスについては、黒マスで矛盾しないことが明らかなので黒マスと仮定することはわざわざしません。白のマスについても同様です

leftAlignLineCells関数 と fixLineCells関数のお試し

文章で説明するよりも、体験した方が理解しやすいと思いますので、お試しください

See the Pen ワンラインお絵かきロジック by takanaweb5 (@takanaweb5) on CodePen.

全体のロジック

ソースはこちらのGithubリポジトリにあります

一次元背理法(後述の二次元背理法に対して)

確定できるマスがなくなるまで、すべての行と列に対してfixLineCells関数を実行し続けます

二次元背理法

もしも一次元背理法でパズルが完成しなかった場合に、以下のロジックを実行します
一次元背理法で確定できなかったマスを１つ選択し、
黒マスと仮に確定して一次元背理法を実行し、エラーになれば白で確定、エラーにならなければ白マスと仮に確定して同じことを行います
上記を確定できるマスがなくなるまで繰り返します

全ての未確定マスについて仮定を実行すると非効率なのでパフォーマンスを重視して、隣接するマスが確定マスか四隅の境界にあるマスのみを対象としています

※雑誌等で紹介されている問題では、一次元背理法で完成し二次元背理法を使うことはほとんどないと思います

注意事項

解が複数の問題では、この手法では問題を完成させることが出来ません
例えば次のようなヒントの時です

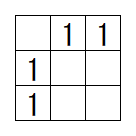
最後に

パズルを解く過程をアニメーションするために以下の記事の手法を使っています

TypeScriptを直接読み込んで実行するために以下の記事の手法を使っています

この記事のアルゴリズムが理解出来てなるほどと思われた方はぜひいいねお願いします