やりたいこと
PRML10章で紹介される一変数ガウス分布の変分事後分布のプロットを行います。混合ガウスや前回に私が書いた分解の近似は意外と記事になっているのですが、一変数ガウスの変分推論は予測分布のプロットが多くて、事後分布自体をプロットする記事はあまり見かけませんでした。「PRMLの事後分布のプロットしたいよ!」という方の参考になれば幸いです。
平均未知、分散未知のガウス分布
観測データが平均と精度が未知のガウス分布から取り出されるとすると、観測データの共役事前分布はガウスガンマ分布となります。ここで注意したいのは、ガウスガンマ分布はガウス分布とガンマ分布の単純な積で表されているわけではありません。ガンマ分布から取り出される値によってガウス分布の精度が変化します。
観測値の事前分布:
P_{rior}( \mu, \lambda ) = N( \mu | \mu_{0} , ( \lambda_{0} \tau )^{-1} )Gam( \tau | a_{0}, b_{0} )
事後分布は厳密に求まり、ガウスガンマ分布になります。
P_{osterior}( \mu, \tau | D ) = N( \mu | \mu_{N} , ( \lambda_{N} \tau )^{-1} )Gam( \tau | a_{N}, b_{N} ) \\
\begin{align}
\mu_{N} &= \frac{ \Sigma_{n=1}^{N} x_{n} + \lambda_{0} \mu_{0} }{ \lambda_{N} } \\
\lambda_{N} &= N + \lambda_{0} \\
a_{N} &= a_{0} + \frac{N}{2} \\
b_{N} &= b_{0} + \frac{1}{2} ( \Sigma_{n}^{N} x_{n}^2 + \lambda_{0} \mu_{0}^{2} - \lambda_{N} \mu_{N}^{2} ) \\
\end{align}
ただし、$D = { x_{1}, x_{2}, ... , x_{N} }$は観測データです。
さて、変分推論では分布を独立な積で表すことができるという仮定を置きます。1変数ガウス分布の事後分布を変分推論の枠組みで考えると、近変分事後分布は次のようになります。解析的に求められる事後分布とは違い、各分布の確率変数が独立に生成されることがわかります。
変分事後分布:
q( \mu, \lambda ) = N( \mu | \mu_{N} , \lambda_{N}^{-1} )Gam( \tau | a_{N}, b_{N} )
パラメータの更新式
今回も前回同様に更新式のみを取り上げます。詳しい計算はPRMLの演習問題2.44でググるとたくさんでてきますので、そちらを参考にしてください。なるべく実装と同じような式変形で表したいと思っているので、$b_{N}$は展開していることに注意してください。
\begin{align}
\mu_{N} &= \frac{ \lambda_{0} \mu_{0} + N \bar x }{ \lambda_{0} + N } \\
\lambda_{N} &= (\lambda_{0} + N )E[\tau] \\
a_{N} &= a_{0} + \frac{N + 1}{2} \\
b_{N} &= b_{0} + \frac{1}{2} ( ( N + \lambda_{0} )E[\mu^{2}] -2E[\mu]( \Sigma_{n}^{N} x_{n} + \lambda_{0} \mu_{0} ) + \Sigma_{n}^{N} x_{n}^{2} + \lambda_{0} \mu_{0}^{2} ) \\
\end{align}
式を見ると、分布のパラメータはお互いのモーメントに依存し合っていることがわかります。なのでパラメータを更新するときは、例えばまず$E[\tau]$を初期化、その後ガウス分布のパラメータを更新します。更新されると$E[\mu],E[\mu^{2}]$が計算できるのでこれらのモーメントを用いてガンマ分布のパラメータを更新すします。以上を繰り返していきます。
では各分布のモーメントを見てみましょう。PRMLでは、なだらかな無情報事前分布を導入していますが、本記事ではパラメータは0にせず式変形を行います。
\begin{align}
E[\mu] &= \mu_{N} \\
E[\mu^{2}] &= \frac{ 1 }{ ( \lambda_{0} + N )E[\tau] + E[\mu]^{2} } \\
E[\lambda] &= \frac{ a_{N} }{ b_{N} } \\
\\
∵\lambda_{N} &= ( E[\mu^{2}] - E[\mu]^{2} )^{-1} = (\lambda_{0} + N )E[\tau] \\
\end{align}
実装
実装に際して、私が一番悩んだことを説明します。それは疑似データの作り方です。単純に平均と分散を決めて乱数を出してはいけません。例えば、平均0.、分散1.のガウス分布から疑似データを取り出すとき、事前分布は( 0.、1. )を中心としたデルタ分布を仮定していることになります。
ベイズ推定は観測データを条件とする事後分布から物事を議論します。今回はパラメータについて議論したいためパラメータの事後分布を設計する必要があります。そして事後分布を計算するには基本的にすべてのパラメータ、観測データまた未知のデータに関する結合分布を設計します。なので観測データを生成する分布というのは、全枠組みの結合分布の観測データに関する周辺分布のことを指します。
p(x) = \int p( x, \mu, \lambda ) d \mu d \lambda = \int p( x | \mu, \lambda )p(\mu | \lambda)p(\lambda) d \mu d\lambda
今回の例を見てみると疑似データ、すなわち観測データを平均0.分散1.のガウス分布とする場合、次のような分布を設計していることになります。
p(x) = \int p( x, \mu, \lambda ) d \mu d \lambda = \int p( x | \mu, \lambda )\delta( \mu - 0 )\delta( \lambda - 1 ) d \mu d\lambda
これでは事後分布が所望のガウスガンマ分布ではなく(0.、1.)を中心とするデルタ分布なので、今回の要件には正しくありません。以上のように疑似データを作るときはパラメータの事後分布をどのような設計にするのかを考える必要があります。
今回は事後分布をガウスガンマ分布で設計するため、疑似データを生成するガウス分布のパラメータもガウスガンマ分布から取り出した値を使用するべきです。実装ではcreate_data( obs_n, p::param )で疑似データを生成しています。疑似データの作り方は、まずガンマ分布から精度部分を取り出します。その精度を使って今度はガウス分布から平均部分を取り出します。最後に取り出したそれぞれの平均と精度を使ってデータを生成します。
function create_data( obs_n, p::param )
N = obs_n
data = zeros(N)
for i in 1:N
λ = rand( Gamma( p.a, p.b ) )
mu = rand( Normal( p.μ, ( p.λ*λ )^-0.5 ) )
data[i] += rand( Normal( mu, λ^-0.5 ) )
end
data
end
ソースコード
module uni_gauss_variations
using Distributions
using Plots
using StatsPlots
using LinearAlgebra
using Random
const rng = MersenneTwister(20210701)
# パラメータ
mutable struct param{T}
μ::T
λ::T
a::T
b::T
end
# ガウスガンマ分布のパラメータの更新
# PRML p185
function q_gauss!( poster_variations::param, prior::param, expectations, data )
N = size(data)[1]
expectations[2] = ( prior.λ*prior.μ + N*mean( data ) ) / ( prior.λ + N ) # E[μ]
expectations[3] = 1 / ( prior.λ + N )expectations[1] + expectations[2]^2.0 # E[μ^2]
poster_variations.μ = expectations[2]
poster_variations.λ = (prior.λ + N) * expectations[1] # E[τ] = expectations[1]
end
function q_gamma!( poster_variations::param, prior::param, expectations, data )
N = size(data)[1]
poster_variations.a = prior.a + (N + 1) / 2
poster_variations.b = prior.b + ((N + prior.λ)expectations[3] -2expectations[2]*( sum( data ) + prior.λ*prior.μ )
+ sum(data.^2) + prior.λ*prior.μ^2) / 2
expectations[1] = poster_variations.a / poster_variations.b # E[τ]
end
# 事後確率を解析的に求める
function posterior( prior::param, data )
N = size( data )[1]
λ = N + prior.λ
μ = ( sum( data ) + prior.λ*prior.μ ) / λ
a = prior.a + N / 2
b = prior.b + ( sum( data.^2 ) + prior.λ*prior.μ^2 - λ*μ^2 ) / 2
param( μ, λ, a, b )
end
# 解析的に求めた事後分布の確率密度
function create_gauss_gamma_pdf( p::param, gauss_range, gamma_range )
N = size(gauss_range)[1]
X = zeros( N, N )
for (idx, i) in enumerate(gauss_range)
for (idy, j) in enumerate(gamma_range)
# プロットは行がx軸に対応して、列にy軸が対応する
X[idy,idx] = pdf.( Normal( p.μ, (p.λ*j)^-0.5 ), i ) * pdf.( Gamma( p.a, p.b ), j )
end
end
X
end
# 近似した事後分布の確率密度
function create_variation_gauss_gamma_pdf( p::param, gauss_range, gamma_range )
N = size(gauss_range)[1]
X = zeros( N, N )
for (idx, i) in enumerate(gauss_range)
for (idy, j) in enumerate(gamma_range)
# プロットは行がx軸に対応して、列にy軸が対応する
X[idy,idx] = pdf.( Normal( p.μ, (p.λ)^-0.5 ), i ) * pdf.( Gamma( p.a, p.b ), j )
end
end
X
end
# ガウス分布とガウスガンマ分布の結合分布のガウスガンマ分布に関する周辺分布からデータを生成
function create_data( obs_n, p::param )
N = obs_n
data = zeros(N)
for i in 1:N
λ = rand( rng, Gamma( p.a, p.b ) )
mu = rand( rng, Normal( p.μ, ( p.λ*λ )^-0.5 ) )
data[i] += rand( rng, Normal( mu, λ^-0.5 ) )
end
data
end
function main()
# データの事前分布
prior = param( 0.0, 2.0, 2.0, 3.0 )
# データの生成
N = 10
data = create_data( N, prior )
# パラメータの事前分布
p = param( 0.0, 0.0, 0.0, 0.0 )
# パラメータの真の事後分布
poster = posterior( p, data )
length= 201
gauss_range = range( -1, 1, length=length )
gamma_range = range( 0, 20, length=length )
# 真の事後分布の確率密度
poster_pdf = create_gauss_gamma_pdf( poster, gauss_range, gamma_range )
# τの期待値と近似分布のパラメータの初期化
expected_τ = expected_μ = expected_square_μ = 1.0
poster_variations = param( 10.0, 2.0, 10.0, 30.0 )
expectations = [ expected_τ, expected_μ, expected_square_μ ]
anim = @animate for n in 1:10
if n % 2 == 1
variations_pdf = create_variation_gauss_gamma_pdf( poster_variations, gauss_range, gamma_range )
contour( gauss_range, gamma_range, poster_pdf, levels=5, title="n = $n" )
contour!( gauss_range, gamma_range, variations_pdf, levels=5 )
q_gauss!( poster_variations, p, expectations, data )
else
variations_pdf = create_variation_gauss_gamma_pdf( poster_variations, gauss_range, gamma_range )
contour( gauss_range, gamma_range, poster_pdf, levels=5, title="n = $n" )
contour!( gauss_range, gamma_range, variations_pdf, levels=5 )
q_gamma!( poster_variations, p, expectations, data )
end
end
# gif画像保存
gif( anim, "variation.gif", fps=5 )
end
end
実際に動かしてみます。分布が形を変えて動いているほうが変分のプロットです。おにぎり型の分布も少し動いていますがこれはプロットの関係で動いてしまっているだけで、パラメータは何も変わっていません。
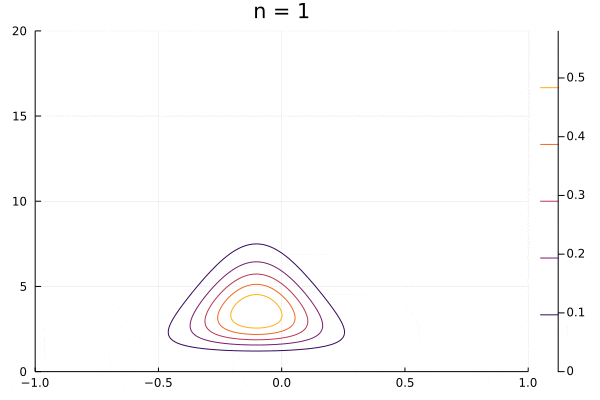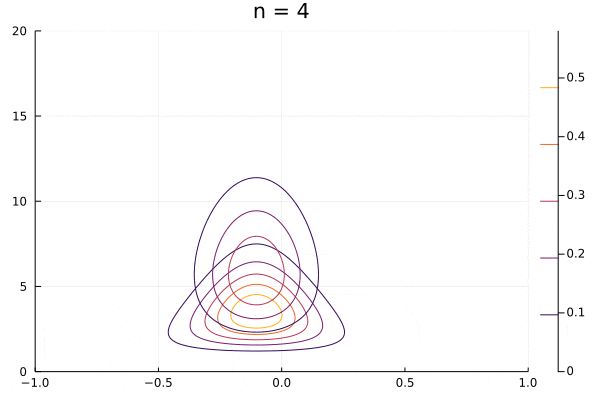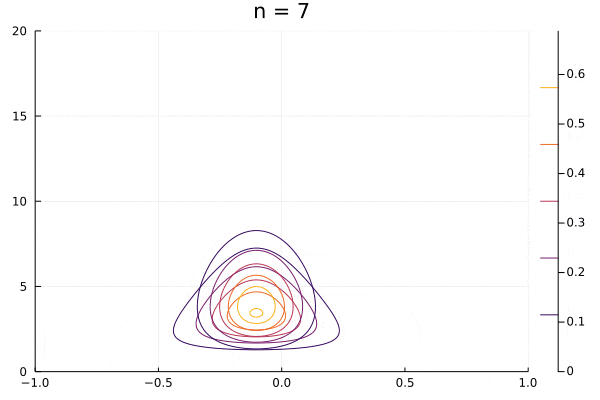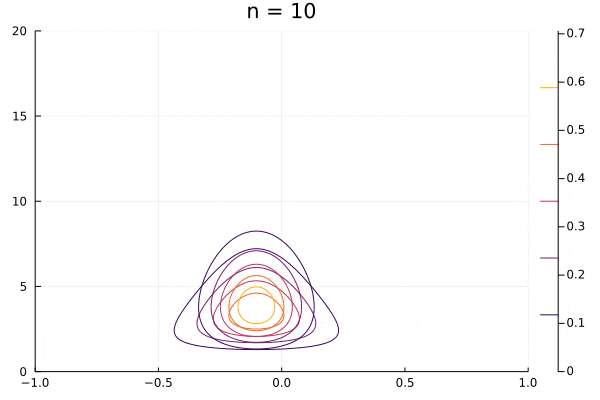
勉強するにあたってはまったこと
- もっとPRMLの画像に似せたかったのですがここら辺が限界でした。初期値をもっと調整すれば似せられるかもしれません。
- ベイズ推定の式は、確率変数とパラメータが似たような文字を使うのでごちゃごちゃになって混乱しました。例えば、$\mu$とかたくさん出てきますが、その出てきた$\mu$は確率変数なのかパラメータなのかを意識することですっきり物事を考えられるようになります。
- データの生成部分はなかなか理解できなかった部分です。観測分布は結合分布の周辺分布であるということをいったん受け入れると話がすんなり進みます。