やりたいこと
変分推論は真の事後分布を分解によって近似します。今回はPRML下巻10.1.2を参考に実際にパラメータの事後分布のパラメータを計算、プロットをJuliaで書いてみます。
ソースコードは須山さんのブログを参考にしました。
パラメータの更新式
詳しい計算は、須山さんのブログがわかりやすいのでそちらを参考にしてください。ここではパラメータの更新の式だけ書いておきます。
今回は二変数ガウス分布を以下の1変数ガウス分布で表せると仮定します。
q(\boldsymbol{z}) = q_{1}(z_{1})q_{2}(z_{2})
$q(\boldsymbol{z})$に対して、求めたい分布の因子以外の因子について期待値を取り、
\log q_{1}(z_{1}) = E_{z_{2}}[ \log q(\boldsymbol{z}) ] + const \\
\log q_{2}(z_{2}) = E_{z_{1}}[ \log q(\boldsymbol{z}) ] + const
計算を進めていくとそれぞれ$z_{1}, z_{2}$についての二次の式となるので、分布$q_{1}(z_{1}), q_{2}(z_{2})$はガウス分布となります。
q_{1}(z_{1}) = N( z_{1} | m_{1}, \lambda_{11}^{-1} ) \\
q_{2}(z_{2}) = N( z_{2} | m_{2}, \lambda_{22}^{-1} ) \\
m_{1} = \mu_{1} - \lambda_{11}^{-1}\lambda_{12}( E_{z_{2}}[z_{2}] - \mu_{2} ) \\
m_{2} = \mu_{2} - \lambda_{22}^{-1}\lambda_{21}( E_{z_{1}}[z_{1}] - \mu_{1} ) \\
ここで、$E_{z_{1}}[z_{1}] = m_{1}, E_{z_{2}}[z_{2}] = m_{2}$であるので、パラメータの更新式は相互に依存し合います。これは連立方程式が解け、直ちに$m_{1} = \mu_{1}, m_{2} = \mu_{2}$となりますが、今回はパラメータの収束の様子を見るので、パラメータは交互に更新させます。うまく更新ができると、平均はきちんと近似できることになります。
各分布は独立であると仮定しているので、共分散行列の対角成分は0になります。また、非対角成分は分解した分布の分散に等しくなります。つまり、分散はうまく表せないことが予想されます。
では実際に見てみましょう。
ソースコード
using Distributions
using Plots
using StatsPlots
using LinearAlgebra
function update_param!( m, μ, λ )
m[1] = μ[1] - inv(λ[1,1])*λ[1,2]*(m[2] - μ[2])
m[2] = μ[2] - inv(λ[2,2])*λ[2,1]*(m[1] - μ[1])
end
function main()
# truth dist
true_μ = [0.0, 0.0]
# 回転行列は直行行列でもある
theta = 2.0*pi/12
A = reshape([cos(theta), -sin(theta),
sin(theta), cos(theta)], 2, 2)
true_Λ = inv(A * inv(reshape([1,0,0,10], 2, 2)) * A')
# init
# プロットがきれいになりそうな値で初期化した
m = [3.0,7.0]
Λ = [true_Λ[1,1] 0;0 true_Λ[2,2]]
anim = @animate for i in 1:20
update_param!( m, true_μ, true_Λ )
covellipse( true_μ, inv(true_Λ), xlim=[-2, 2], ylim=[-2, 2], title= "n=$i", label="truth_dist" )
plot!( [true_μ[1]], [true_μ[2]], markershape=:x, markersize=5, label=false )
covellipse!( m, inv(Λ), color="blue", coloralpha=0.3,label="approximate_dist" )
end
gif( anim, fps=5 )
end
main()
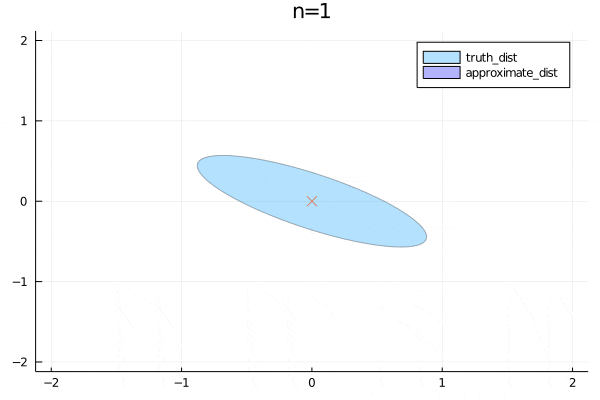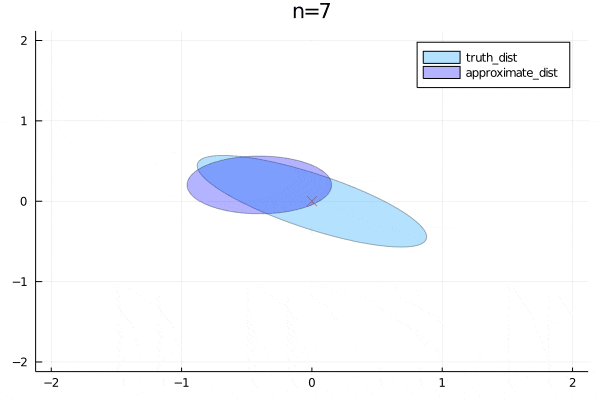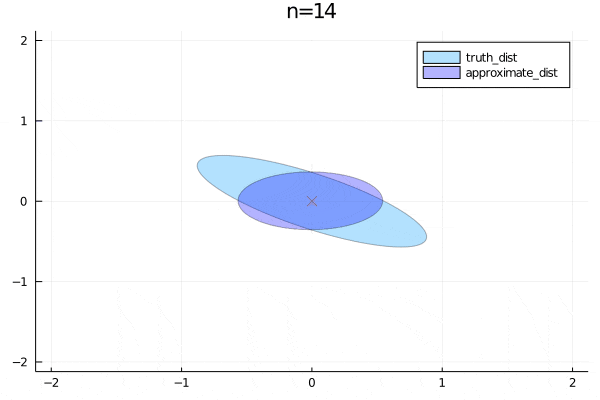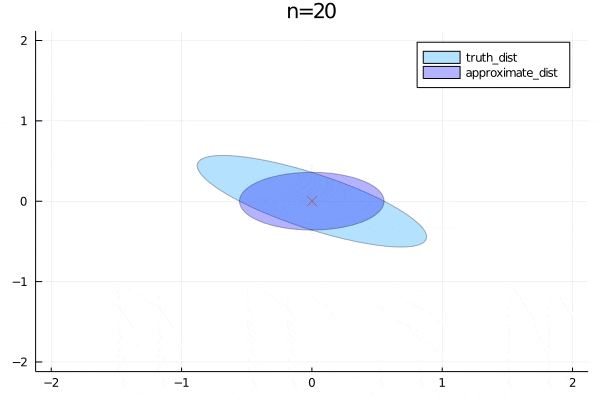
まずは平均についてです。パラメータを更新すると徐々に真の分布の平均に近づくことがわかります。分散は非対角成分が0なので変数間の関係をうまく表せていないことがわかります。
勉強するにあたってハマったとことか
- 近似した事後分布の共分散行列の非対角成分は、分布同士が独立という仮定を置いているので$\lambda_{12}=\lambda_{21}=0$です。でも、パラメータの更新に使う共分散行列の非対角成分は、0ではないので注意しましょう。(私はプログラムを書くときにごっちゃになったので覚書として)
- 正定値行列を作るのに、今までは固有値が全て正になるように行列の成分をいちいち調整していたのですが、回転行列という直行行列を使うことで、簡単に正定値行列を作れることを須山さんのソースコードで知りました。
- juliaでgifを作るのやり方はここを参考にしました。
PCAでも同じことができる?
データにPCA(主成分分析)を適用し個々のデータの相関をなくしたうえで、パラメータを推定すれば同じ結果が出るのではないか、と上司にアドバイスを頂いたので次はそれもやってみたいと思います。