Rでガウス分布の平均・精度パラメータを変分ベイズ推定

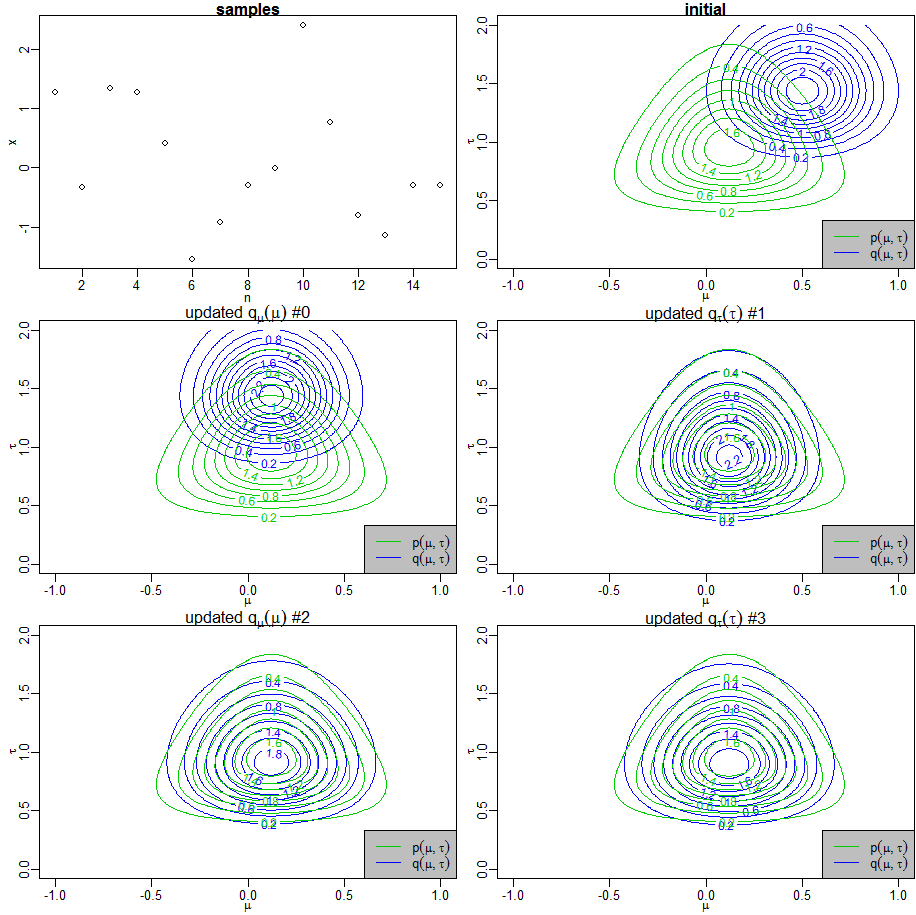
PRML図10.4と同様に、ガウス分布の平均・精度パラメータに関する共役事前分布に対して、厳密に求めた事後分布と、変分近似した事後分布の等高線を重ねて、変分近似の過程を描画します。また、与えたデータ集合も描画します。

まず、ガウス分布$N(x_n|\mu,\tau^{-1})$から独立に生成されたデータ$\mathbf{X}=(x_1,\dots,x_N)$が与えられたとき、平均パラメータ$\mu$と精度パラメータ$\tau$に関する共役事前分布は、以下のガウスガンマ分布となります。(PRML 2.3.6参照)

p(\mu,\tau)=p(\mu|\tau)p(\tau)=N(\mu|\mu_0,(\lambda_0\tau)^{-1})Gam(\tau|a_0,b_0)

ここでは、この共役事前分布に対する事後分布$p(\mu,\tau|\mathbf{X})$を分解して、事後分布の変分近似$q(\mu,\tau)=q_\mu(\mu)q_\tau(\tau)$を求めます。なお実際には、PRML演習2.44の通り、事後分布は以下の形で厳密に求まります。

\begin{aligned}
p(\mu,\tau|\mathbf{X}) &= N(\mu|\mu_N,(\lambda_N\tau)^{-1})Gam(\tau|a_N,b_N) \\
\mu_N &= \frac{N\mu_{ML}+\lambda_0\mu_0}{N+\lambda_0} \\
\lambda_N &= \lambda_0+N \\
a_N &= a_0+\frac{N}{2} \\
b_N &= b_0+\frac{1}{2}\left(N\sigma^2_{ML}+\frac{\lambda_0 N(\mu_{ML}-\mu_0)^2}{\lambda_0+N}\right)
\end{aligned}

変分近似により、最適な因子$q_\mu^\star(\mu),q_\tau^\star(\tau)$を求めると、以下のようになります。

\begin{aligned}
q_\mu^\star(\mu) &= N(\mu|\mu_N,\lambda_N^{-1}) \\
\mu_N &= \frac{\lambda_0\mu_0+N\bar{x}}{\lambda_0+N} \\
\lambda_N &= (\lambda_0+N)E_\tau[\tau] \\
q_\tau^\star(\tau) &= Gam(\tau|a_N,b_N) \\
a_N &= a_0+\frac{N+1}{2} \\
b_N &= b_0+\frac{1}{2}E_\mu\left[\sum_{n=1}^N(x_n-\mu)^2+\lambda_0(\mu-\mu_0)^2\right] \\
 &=b_0+\frac{N+\lambda_0}{2}E_\mu[\mu^2]-\left(\sum_{n=1}^Nx_n+\lambda_0\mu_0\right)E_\mu[\mu]+\frac{1}{2}\left(\sum_{n=1}^Nx_n^2+\lambda_0\mu_0^2\right)
\end{aligned}

各期待値は、以下のようになります。

\begin{aligned}
E_\mu[\mu] &= \mu_N \\
E_\mu[\mu^2] &= Var(N(\mu|\mu_N,\lambda_N^{-1}))+E_\mu[\mu]^2 \\
 &= \lambda_N^{-1}+\mu_N^2 \\
E_\tau[\tau] &= \frac{a_N}{b_N}
\end{aligned}

適当な初期値から初めて、$q_\mu^\star(\mu), q_\tau^\star(\tau)$を順に更新していき、$q(\mu,\tau)$を求めています。

frame()
set.seed(0)
par(mfrow=c(3, 2))
par(mar=c(2.3, 2.5, 1, 0.1))
par(mgp=c(1.3, .5, 0))
murange <- c(-1, 1)
taurange <- c(0, 2)
mu <- seq(murange[1], murange[2], 0.01)
tau <- seq(taurange[1], taurange[2], 0.01)

# 観測点を生成する
N <- 15
MU <- 0
TAU <- 1
x <- rnorm(N, MU, sqrt(TAU ^ -1))
plot(x, xlab="n", main="samples")

# 平均・精度パラメータの事前分布を設定する
ngmu0 <- 0
nglambda0 <- 1.0E-6  # 平均パラメータの事前分布の分散(nglambda*λ)^-1を大きく取る
nga0 <- 1
ngb0 <- 1.0E-6  # 精度パラメータの事前分布の分散nga/ngbを大きく取る

# 真の事後分布であるガウスガンマ分布のパラメータを求める
uml <- mean(x)
sigma2ml <- var(x) * (N - 1) / N
nga <- nga0 + N / 2
ngb <- ngb0 + (N * sigma2ml + nglambda0 * N * (uml - ngmu0) ^ 2 / (nglambda0 + N)) / 2
ngmu <- (N * uml + nglambda0 * ngmu0) / (N + nglambda0)
nglambda <- nglambda0 + N

# 適当な初期値に設定する
muN <- 0.5
lambdaN <- 20
Emu <- muN
Emu2 <- lambdaN ^ -1 + muN ^ 2
aN <- 24
bN <- 16
Etau <- aN / bN

for (iteration in -1:3) {
    if (iteration >= 0) {
        if (iteration %% 2 == 0) {
            # 因子 qmu(mu)=N(mu|muN,lambdaN) を求める
            muN <- (nglambda0 * ngmu0 + sum(x)) / (nglambda0 + N)
            lambdaN <- (nglambda0 + N) * Etau
            Emu <- muN
            Emu2 <- lambdaN ^ -1 + muN ^ 2
        } else {
            # 因子 qtau(tau)=Gam(tau|aN,bN) を求める
            aN <- nga0 + (N + 1) / 2
            bN <- ngb0 + (N + nglambda0) / 2 * Emu2 - (sum(x) + nglambda0 * ngmu0) * Emu +
                (sum(x ^ 2) + nglambda0 * ngmu0 ^ 2) / 2
            Etau <- aN / bN
        }
    }

    # 近似した分布を描画する
    q <- outer(mu, tau, function(mu, tau) {
        dnorm(mu, muN, sqrt(lambdaN ^ -1)) * dgamma(tau, aN, rate=bN)
        });
    contour(mu, tau, q, xlim=murange, ylim=taurange, xlab=expression(mu), ylab=expression(tau), col=4)

    # 真の分布を描画する
    p <- outer(mu, tau, Vectorize(function(mu, tau) 
        dnorm(mu, ngmu, sqrt(1 / (nglambda * tau))) * dgamma(tau, nga, rate=ngb)
        ))
    contour(mu, tau, p, xlab="", ylab="", col=3, add=T)

    legend("bottomright", c(
        expression(p(mu,tau)), 
        expression(q(mu,tau))
        ), col=c(3, 4), lty=1, bg="gray")
    if (iteration >= 0) {
        if (iteration %% 2 == 0) {
            title(bquote(paste("updated ", q[mu](mu), " #", .(iteration))))
        } else {
            title(bquote(paste("updated ", q[tau](tau), " #", .(iteration))))
        }
    } else {
        title("initial")
    }
}