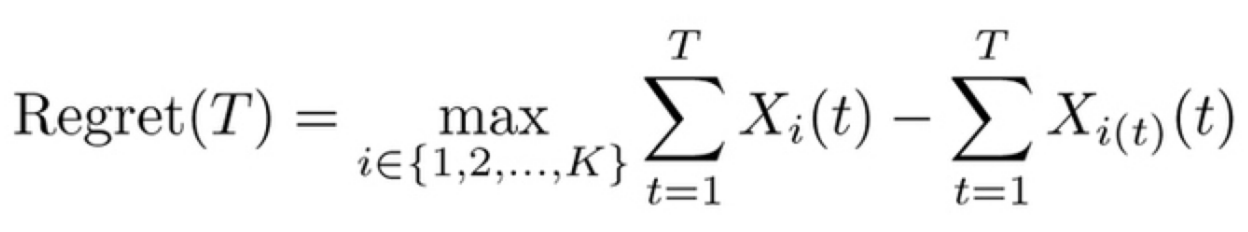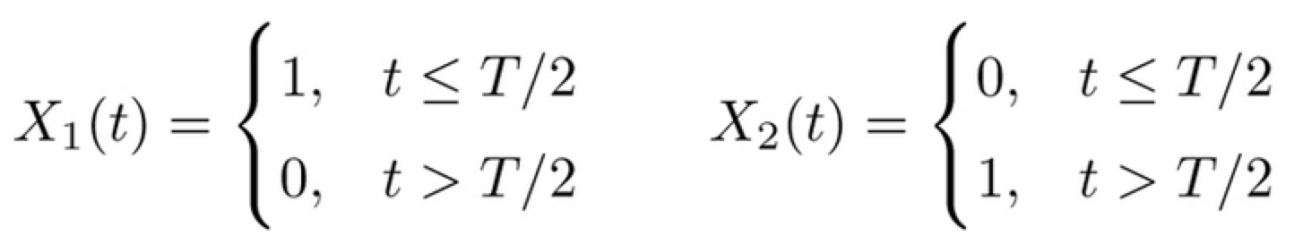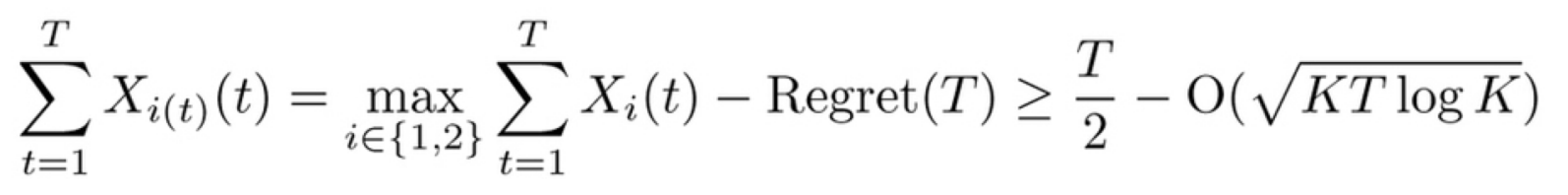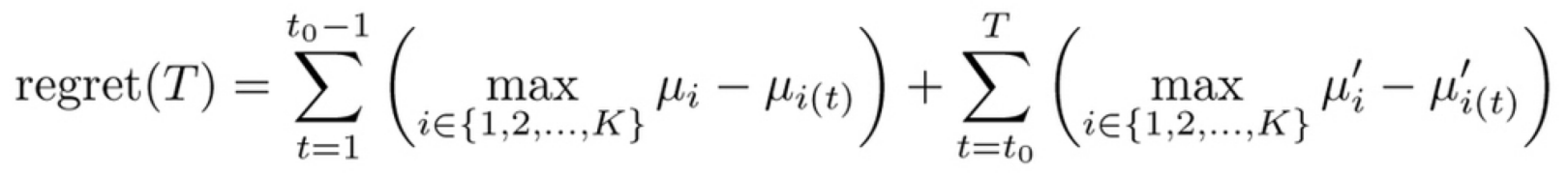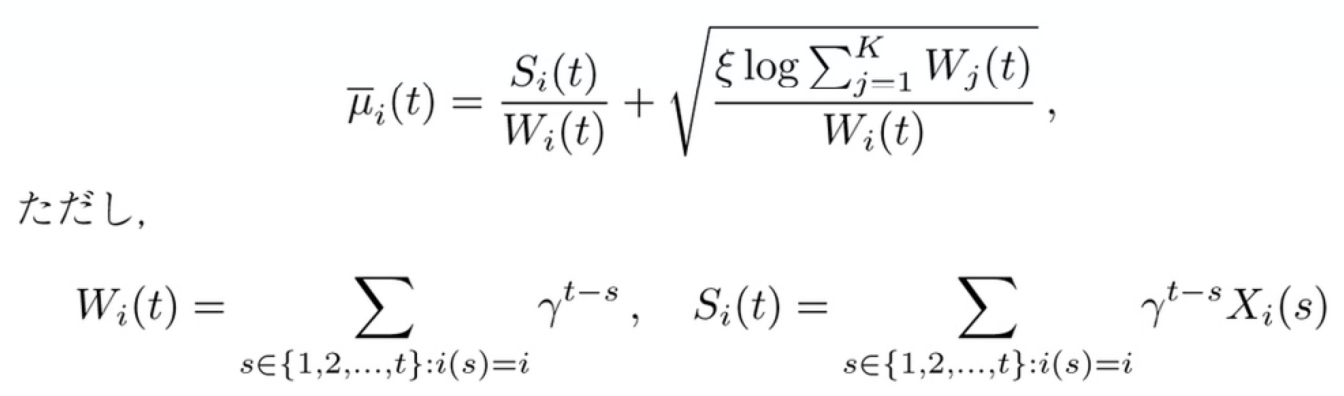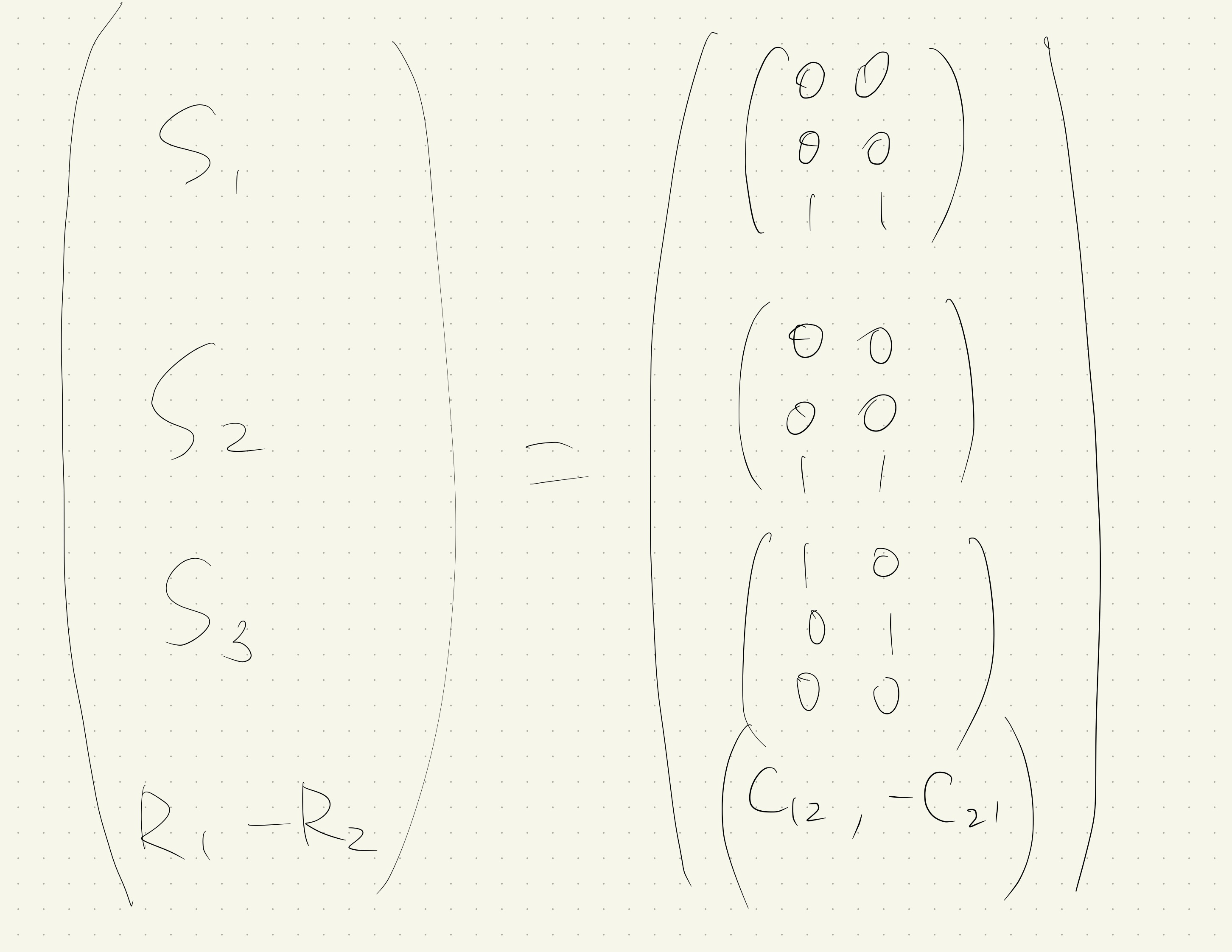はじめに
書籍 バンディット問題の理論とアルゴリズムの9章(p147~p170)のまとめです。
この章では大きく
- アームの報酬確率が時間で変化するバンディット問題
- アームの評価を比較によって行うバンディット問題
- 報酬をそのまま検知することができないバンディット問題
を扱う。
9.1 時間変化のあるバンディット問題
クリックなどの報酬の確率が時刻と共に変化する場合を考える。
例:ニュース推薦(最新のニュースの方がクリックされやすい)
(他に広告などでもありそう(季節性のある商品等))
このような問題に対する定式化としては、
- 文脈つきバンディットに基づく方法
- 敵対的バンディットに基づく方法
が考えられる。
9.1.1 文脈つきバンディットに基づく方法
文脈つきバンディット(Contextual Bandit)とは、
- 時刻tにおける各行動iの特徴量として、$a_{i, t} \in \mathbb{R}^{d}$が与えられているもの
だった。
そこで、この $a_{i,t}$の要素の1つをf(記事iが配信開始されてからの経過時間)にすることを考える。
注意点
報酬期待値の時間変化のパターンがある程度わかってる必要がある。
パターンがあるなら、それを別の特徴量によって表現できるようなモデルを導入する必要
例
- 日焼け対策の記事はクリック率が夏に上がり、冬が下がる
- 新商品の紹介記事は徐々にクリック率が下がっていく
9.1.2 敵対的バンディットに基づく方法
敵対的バンディットは報酬が何らかの確率分布に従うことを仮定していない。
そのため時間変化があるバンディットの様な、「報酬が確率的ではあるが非定常的」な設定も扱える。
しかし、高い累積報酬を達成できるとは限らない。
達成できない理由
敵対的バンディット問題の設定では、リグレットの定義は下記で、これは
- 「常に同じアームを選択し続ける」という方策の内で最良もの(右辺の左側) と
- 実際の累積報酬(右辺の右側)を
比較することを意味している。
そのため、途中で引くアームを変更するような方策と比較することは考慮していない。
例
- アーム数:2
- 時刻はT(偶数)まで
- 前半はアーム1を引くと報酬1、後半はアーム2を引くと報酬1
(昼間は広告1、夜間は広告2がクリックされやすいような場合)
1)敵対的バンディットの設定では比較対象として考えるのは、「アーム1を選択し続ける」または「アーム2を選択し続ける」という方策。
そして上記の例だとその場合の累積報酬はいずれも $T/2$。
2)敵対的バンディットのExp3方策はリグレット上界
$ O(\sqrt{KT\log{K}})$を持つ。
1、2より累積報酬は
を変形して
となることまでしか保証できない。
上記の例での真の最大の累積報酬 $T$ とは $T-(T/2-O(\sqrt{KT\log{K}})=O(T)$ の差がある。
この様に、敵対的バンディットが高い累積報酬を達成できるとは限らない。
- 時間的変化はするが最良な選択は変わらない(クリック率の順位は変わらない)場合には有効と考えられるが、
- 最良の選択が変わるような場合には必ずしも高い累積報酬を達成できない
9.1.3 有限回の時間変化がある場合
確率的な設定として、下記のような報酬分布の組を考える。
\left\{\mu_{i}, \mu_{i}^{\prime}\right\}_{i=1}^{K}
各アーム$i$からの報酬はある時点$t_0$を境に変化する。
K=3の時の例
| アーム $i$ | 1 | 2 | 3 |
|---|---|---|---|
| $\mu_i$ | 0.4 | 0.5 | 0.6 |
| $\mu'_i$ | 0.9 | 0.4 | 0.3 |
- 時刻 $t \leq t_0$では$\rm{Ber}(\mu_i)$に従い、
- 時刻 $t \gt t_0$では$\rm{Ber}(\mu'_i)$に従う
ここで、
- $t_0$と前後の報酬分布がわかっている場合の最大の期待報酬と
- 実際の報酬期待値の差
は下記の式で表される。
プレイヤーはこの値の最小化を目指す。
この問題ではどのような方策を用いたとしても任意の十分大きい $T$ でリグレットが
$$\mathbb{E}[\operatorname{regret}(T)]=\Omega(\sqrt{T})$$
となることが知られている。
確率的バンディットにおいて確率分布の変化点がある場合の単純な方策としては割引UCB方策がある。
- $\sqrt{\frac{\log t}{2 N_{i}(t)}}$は信頼区間の上限と平均の差
- $N_i(t)$はアーム$i$をt時点までに選んだ回数
- 割引UCBは直近のスコアを重要視する加重平均
- そのため確率分布に時間変化がある場合にも適応的に探索できる
- $\gamma$は時刻が1離れた時の割引率
- $\xi$は信頼区間の上限を調整するパラメータ(?)
結果
- パラメータを調整することで、リグレットを$\mathrm{O}(\sqrt{c_{T} T} \log T)$と抑えられる
- 敵対的バンディットではExp3.S方策を用いることで同様のリグレット上界
9.1.4 その他の手法
- 睡眠型バンディット:時刻ごとに選択可能なアームが変化する
- 滅亡型バンディット:各アームについて選択可能な回数の上限がある
- 非休止型バンディット:各アームに有限通りの状態があり引かれなかったアームについても、その状態がマルコフ的に変化する
9.2 比較バンディット
この本のこれまで:報酬は明示的に観測される(クリックの有無など)
比較バンディット:相対評価を観測する。それに基づいて全体として「良い」候補を提示する(映画など)
例:9.1 交互配置フィルタリング
いくつかある検索アルゴリズムのうち、どれが最も良いかを探る様な場合
- 検索アルゴリズムのペアを選ぶ
- それぞれのアルゴリズムの結果を交互に混ぜたものを表示する
- クリックされた方の結果を出したアルゴリズムが、もう一方のアルゴリズムより好まれたと見なす
- これを繰り返し、ペアとして最も良いアルゴリズム同士を選ぶ様になることを目指す。
9.2.1 定式化
- K個のスロットマシーンのアームがある
- アームの各ペアには未知の確率 $\mu_{i,j} = $「アームiがアームjに勝利する確率」が定まっている
- プレイヤーは時刻$t$に、それらのアームからペア($i_1(t),i_2(t)$)を選ぶ
- プレイヤーは$i_1(t),i_2(t)$のどちらかが勝ったかという情報を確率$\mu_{i,j}$に従って観測する
- (この勝ち負けでプレイヤーの報酬が決まるわけではない。どちらかが勝ちどちらかが負けるだけ)
ここで、
- $\mu_{j,i} = 1 - \mu_{i,j}$(アームjがアームiに勝つ確率は、アームiがアームjに勝つ確率を1から引いたもの)
- $\mu_{i,i} = 1/2$と定義
🤔プレイヤーがしたいのは、「良いアーム」を選ぶこと。「良いアーム」を選んでいる時に報酬が高くなる様に定式化したい。
ただ比較バンディットは複数の人間の曖昧な選好関係を考えるモデルであるため、報酬や良いアームの定義が一つに定まり辛い。
定りづらい例:アーム間の勝敗関係が循環系(ジャンケン)になっていて、
「相対的に最も良いアーム」を定義できない場合
そのため比較バンディットの定式化では、各アームのペアの勝率の組み合わせ
\left\{\mu_{i, j} \right\}_{(i, j) \in \{1,2, ..., K\}^{2}}
に何らかの制約を入れることが多い。
制約の代表的なものとして、
- コンドルセ勝者の仮定
がある。
なお、この後で、
- ボルダ勝者
- コープランド勝者
も出てくる。これらは常に存在する勝者の定式化。
コンドルセ勝者は必ずしも存在しない(が経験的に多くの場面で存在する)ため「仮定」としている。
コンドルセ勝者
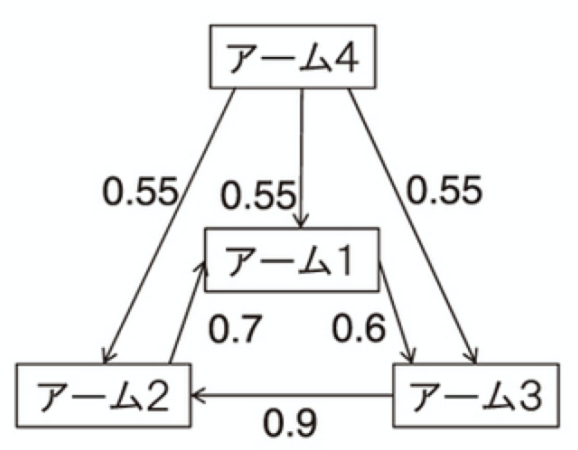
コンドルセ勝者とは、他の全てのアームに対して $1/2$ より大きい確率で勝利するアームのこと。
必ずしも存在するわけではないが、この様な存在を仮定してしまう。
(経験上、たいていの場合にこの様なアームが存在するらしい。)
↑アーム4がコンドルセ勝者。なお1〜3は循環になっている。(許容される)
コンドルセ勝者の損失例1
コンドルセ勝者 $i^*$が存在する場合の損失の例としては下記がある。
\begin{aligned} l(t) &=\left(\mu_{i^{*}, i_{1}(t)}-1 / 2\right)+\left(\mu_{i^{*}, i_{2}(t)}-1 / 2\right) \\ &=\mu_{i^{*}, i_{1}(t)}+\mu_{i^{*}, i_{2}(t)}-1 \end{aligned}
↑ある時刻$t$でペアとしてアーム$i_1(t)$とアーム$i_2(t)$を選んだときの損失
$l(t)=0$となるのは$i_1(t) = i_2(t) = i^*$としたとき。
コンドルセ勝者以外を選んだとき、コンドルセ勝者との勝率が$1/2$に近いほど(拮抗してるほど)損失は小さくなる。
プレイヤーのregretは時刻1〜Tを合計して
\operatorname{regret}(T)=\sum_{t=1}^{T} l(t)
コンドルセ勝者の損失例2
映画や音楽の推薦では同じ候補を2つユーザーに提示するのは無意味とも考えられる。その様な場合には損失を下記の様に考えることができる。
l(t)=\mathbb{1}\left[i_{1}(t) \neq i^{*} \land i_{2}(t) \neq i^{*}\right]
↑2つ提示した候補のうちいずれかがコンドルセ勝者となっていれば損失0。
なお上記の定義のもとでのリグレットを「弱リグレット」と呼ぶ。
ボルダ勝者
- 「対戦相手」がK個のアームを一様ランダムに選択したと仮定したときにその対戦相手に対する勝率が最も高くなるアーム
- 言い換えると、各アームごとに、その他のアームとの勝率から平均勝率を求め、その平均勝率が最も高いアームをボルダ勝者とする(同じアーム同士の勝率も計算に用いることもあるが、ボルダ勝者は変わらない)
i_{\mathrm{Borda}}^{*}=\underset{i \in\{1,2, \ldots, K\}}{\operatorname{argmax}} \frac{1}{K} \sum_{j=1}^{K} \mu_{i j}=\underset{i \in\{1,2, \ldots, K\}}{\operatorname{argmax}} \frac{1}{K-1} \sum_{j \neq i}^{K} \mu_{i j}
↑
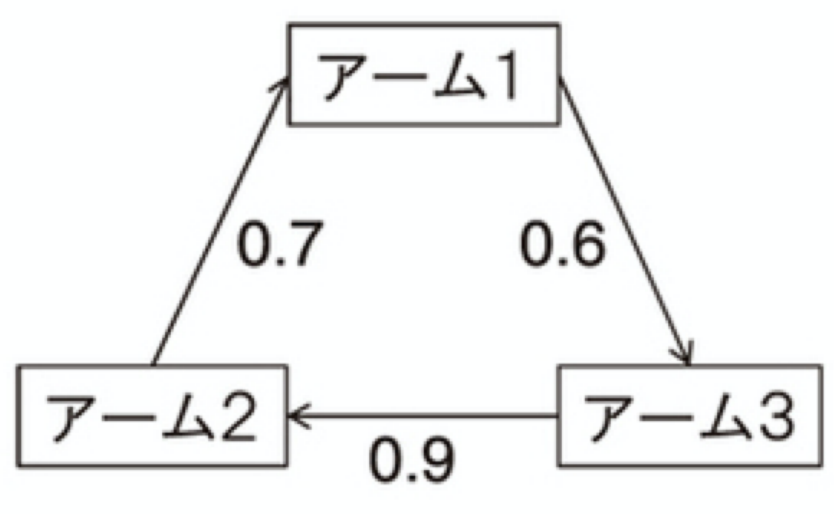
アーム1:アーム2に対して0.3,アーム3に対して0.6なので0.45
アーム2:アーム1に対して0.7,アーム3に対して0.1なので0.4
アーム3:アーム1に対して0.4,アーム2に対して0.9なので0.65
よってアーム3がボルダ勝者
コープランド勝者
勝ち越す相手が最も多いアームをコープランド勝者と呼ぶ(勝率が $1/2$ より大きいか否かしか見ない)
i_{\text {Copeland }}^{*}=\underset{i \in\{1,2, \ldots, K\}}{\operatorname{argmax}} \sum_{j=1}^{K} \mathbb{1}\left[\mu_{i j}>1 / 2\right]
↑アーム1,2,3共に勝ち越すアームが1つのため、全てコープランド勝者。
9.2.2 比較バンディットの方策
比較バンディットでは、トンプソン抽出を行っても、同じアームをペアとして選択するだけで、意味のある結果が得られない。
🤔よくわからない
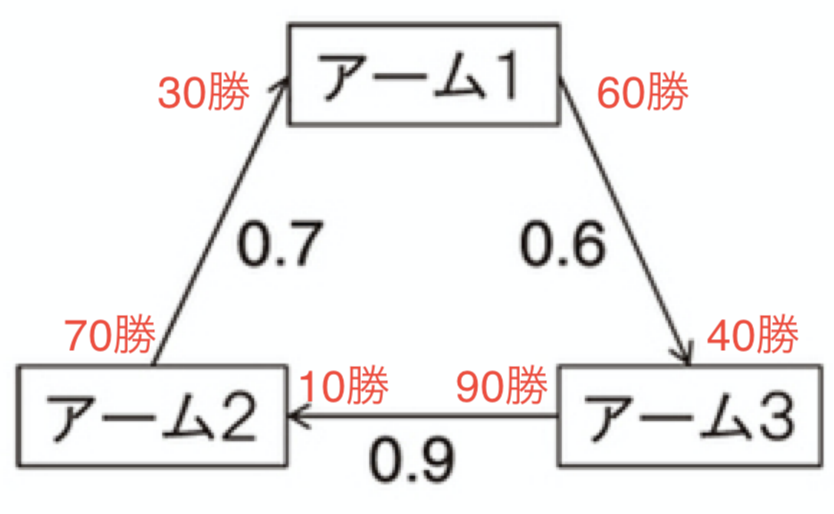
例えばアームのペアを100回ずつ、合計300回候補に選び、上記の様な勝率になっていたとする。
このときトンプソン抽出では、
- 各アーム間の勝率をトンプソン抽出で求め(?)
- その勝率が正しいものとして最適となる行動を取る。ボルダ勝者の規準やコープランドの規準のどれを選ぶにせよ、最適となる行動は、サンプリングで求めた候補のペアとしてその規準の上で最も良いアームをを2つペアとして選ぶこと。
- 同一のアーム同士の比較のみが行われてしまい、意味のある情報が得られない
(🤔ペアの一方を選ぶごとにパラメータをトンプソン抽出で選び直せばいいのでは?と思ったが、
プレイヤーが行うことは「ペアを選ぶ」であり、そのため行うパラメータ抽出は1回のみ、ということか?)
9.2.2.1 ボルダ勝者のための方策
ボルダ勝者は
\bar{\mu}_{i} .=\frac{1}{K-1} \sum_{j \neq i}^{K} \mu_{i j}
が最大になるアームのこと。
アーム $i$の比較対象 $j \neq i$ をランダムに選べば、アーム $i$の $\bar{\mu}_i$は推定できる。
そのため、通常のバンディット問題の方策において「アーム$i$を引く」を「アーム$i$と、ランダムに選んだ $j \neq i$と比較する(ペアに選ぶ)」と置き換えたものを適用すると良い。
リグレットについては下記2つの場合が考えられる。
弱リグレットの場合
弱リグレット(ペアのうちどちらかに最適アームが含まれていれば損失0)を $\rm{O}(K\log{T})$で抑えることができる。
(時刻Tに対しlogオーダーで小さい)
式9.2 や 式9.5の場合
式9.2(コンドルセ勝者の仮定における損失)
\begin{aligned} l(t) &=\left(\mu_{i^{*}, i_{1}(t)}-1 / 2\right)+\left(\mu_{i^{*}, i_{2}(t)}-1 / 2\right) \\ &=\mu_{i^{*}, i_{1}(t)}+\mu_{i^{*}, i_{2}(t)}-1 \end{aligned}
式9.5
l(t)=\left(\bar{\mu}_{i^{*}\cdot} -\bar{\mu}_{i_{1}(t) \cdot}\right)+\left(\bar{\mu}_{i^{*}\cdot} -\bar{\mu}_{i_{2}(t)\cdot}\right)
損失の基準として上記などを用いる場合、損失を0とするにはペアに同じアームを選ぶ必要がある。
いい感じにすることで $\rm{O}(K\log{T})$のリグレットが達成できる。
9.2.2.2 コンドルセ勝者のための方策
ボルダ勝者の規準のもとでは小さいリグレットを比較的容易に達成できた。これは各アームの「良さ」を期待値の和により単純に数値化できるから。
コンドルセ勝者(他の全てのアームに対して $1/2$ より大きい確率で勝利するアーム)や
コープランド勝者(勝率が $1/2$ より大きく勝ち越す相手が最も多いアーム)は
$\mu_{i,j}$がそれぞれ$1/2$より大きいかという関係に依存していて、相対比較による優劣を考える比較バンディット特有の難しさが現れる。
🤔ここからよくわからなかった↓
- $L_C$:現在のループで引くべきアームのリスト
- $L_N$:次のループで引くべきアームのリスト
- DMED方策の本質は「3.11を満たすアームがあったらそれを定数時間内に引く」と言う性質
9.3 部分観測問題
各時刻に
- プレイヤーが行動$i \in \mathcal{I}={1,2, \ldots, K}$を
- 敵対者が内部状態$j \in \mathcal{J}={1,2, \ldots, M}$を
選ぶ。
そして行動と内部状態によって、
- 報酬$r_{i j} \in \mathbb{R}$と
- 信号$h_{i j} \in \mathcal{S}={1,2, \ldots, A}$
が定まる。プレイヤーは信号$h_{ij}$のみ観測する。
(報酬$r_{i j}$を観測することはできない)
報酬行列と反応行列(信号)はそれぞれ既知とする。
例9.3 効率的ラベル予測
画像などへのラベル付作業を考える。
作業者(プレイヤー)の行動は
- アイテムをラベル1に自力で分類
- アイテムをラベル2に自力で分類
- 専門家に正しいラベルを尋ねる
の3つ、
評価者の様な人(敵対者)の内部状態は
- アイテムの正解ラベルは1
- アイテムの正解ラベルは2
の2つがある設定を考える。
この時、報酬と反応は
- タイプ1、タイプ2に自力で分類した場合
- 報酬(損失):間違っていた時、損失$c_jj'>0$を知らず知らずのうちに被る
- 反応:あっていても間違っていても、作業者が得られる反応はなし
- 専門家に正しいラベルを尋ねた場合
- 報酬(損失):手間として損失$q>0$を被る
- 反応:アイテムの正しいラベルが得られる
とする。
つまり、こんな感じ
報酬(観測できない)
| 行動 \ 内部状態 | タイプ1 | タイプ2 |
|---|---|---|
| 自力でタイプ1 | 0 | $-c_{21}$ |
| 自力でタイプ2 | $-c_{12}$ | 0 |
| 専門家に聞く | $-q$ | $-q$ |
反応(観測するもの)
観測できるのは、反応1、反応2、反応3の3パターンのみ。
| 行動 \ 内部状態 | タイプ1 | タイプ2 |
|---|---|---|
| 自力でタイプ1 | 3 | 3 |
| 自力でタイプ2 | 3 | 3 |
| 専門家に聞く | 1 | 2 |
これを行列に書き直した、報酬行列と反応行列は下記。(「信号行列」は改めて出てくる)
R=\left(\begin{array}{cc}{0} & {-c_{21}} \\ {-c_{12}} & {0} \\ {-q} & {-q}\end{array}\right), \quad H=\left(\begin{array}{ll}{3} & {3} \\ {3} & {3} \\ {1} & {2}\end{array}\right)
内部状態$j$は確率分布
p=\left(p_{1}, p_{2}, \ldots, p_{M}\right) \in \mathcal{P}_{M}
に従って時刻ごとに独立に選ばれるものとする。
p=\left(p_{1}, p_{2}, \ldots, p_{M}\right) \in \mathcal{P}_{M}
各行動を選択することによる報酬の期待値ベクトルは
報酬行列$R$に各内部状態が現れる確率$p$をかけることで求まる。($\left(\mu_{1}, \mu_{2}, \ldots, \mu_{K}\right)^{\top}$)
つまり、プレイヤーの取れる各行動に対する期待値がわかる。
期待値最大の行動は
i^{*}=\operatorname{argmax}_{i \in \mathcal{I}} R_{i} p
または、
i^{*}=\operatorname{argmax}_{i \in \mathcal{I}} \mu_i
と表せる。
(なお$i$はとる行動が報酬行列$R$の何行目か)
これはリグレット
\operatorname{regret}(T)=\sum_{t=1}^{T}\left(R_{i^{*}}-R_{i(t)}\right) p
の最小化と同等になる。
例9.3に戻ると
R=\left(\begin{array}{cc}{0} & {-c_{21}} \\ {-c_{12}} & {0} \\ {-q} & {-q}\end{array}\right)
仮に正解ラベル1と2の比率が7:3とすると、
Rp=\left(\begin{array}{cc}{0 \times 0.7 + -c_{21} \times 0.3} \\ {-c_{12} \times 0.7 + 0 \times 0.3} \\ {-q \times 0.7 + -q \times 0.3 }\end{array}\right)
となる。
🤔例えば$c_{12},c_{21}$が$q$と比べて極めて大きい場合(間違ったラベルを付けるとすごい怒られが発生する)なら、i=2(専門家に質問する)が最も期待値の高い行動になるし、逆に専門家への質問コストが大きい場合は、質問せずに選んだ方が良かったりする、のかな。
9.3.2 分類と理論限界
部分観測問題に置いては最悪時に関する解析が多く行われているらしい。
そして達成可能なリグレットは報酬行列 $R$と反応行列$H$の構造により、下記の4つに分けられる。
- 自明な問題
- 簡単な問題(≒自明でなく、局所観測可能な問題)
- 困難な問題(=局所観測可能な問題でなく、大域的観測可能な問題)
- 絶望的な問題(どれにも当てはまらない問題)
そしてある問題がこの分類のどれに当たるかの判断に用いられるのが パレート最適性という概念と、信号行列。
パレート最適性
行動$i$が唯一の最適行動となる様な内部状態の分布があること、
すなわち、
R_{i} p=\max _{i^{\prime} \neq i} R_{i^{\prime}} p
(🤔この式は>ではないか?)
となる様な内部状態の分布$p \in \mathcal{P}_{M}$が存在することをパレート最適であるという。
例9.3を元にすると、
R=\left(\begin{array}{cc}{0} & {-c_{21}} \\ {-c_{12}} & {0} \\ {-q} & {-q}\end{array}\right)
上記で内部状態の分布が(1,0)だった時(つまり正しいラベルが1のみの時)、
行動1が唯一の最適行動になる(行動1のみ報酬(損失)が0。他は負の報酬)。
同様に内部状態の分布が(0,1)の時、行動2が唯一の最適行動。
(🤔行動3(正しいラベルを専門家に尋ねる)はパレート最適でないとされてるが、
上記の報酬行列の$c$と$q$の値次第では、内部状態の分布が(0.5,0.5)などの時にパレート最適になるのでは?)
信号行列
次に反応行列から定まる信号行列($S_{i} \in{0,1}^{|\mathcal{S}| \times|\mathcal{J}|}$)を定義する。
信号行列は行動ごとに作成される。
行が信号の種類、列が内部状態の種類になっている。
例9.3を元にすると、
ユーザーが行動1をとる時、内部状態が何であれ得られる信号は3。
行動2も同様。
行動3は内部状態が1の時信号1を得て、内部状態が2の時信号2を得る。
それを信号行列として表すと下記。
S_{1}=\left(\begin{array}{ll}{0} & {0} \\ {0} & {0} \\ {1} & {1}\end{array}\right), S_{2}=\left(\begin{array}{ll}{0} & {0} \\ {0} & {0} \\ {1} & {1}\end{array}\right), S_{3}=\left(\begin{array}{ll}{1} & {0} \\ {0} & {1} \\ {0} & {0}\end{array}\right)
問題の分類はどの様に行うか
自明な問題
パレート最適な行動が1つしかない時、その問題は自明であると言う。唯一のパレート最適な行動$i$を選び続ければ良い。
(それ以外の行動は、最も最適となる様な内部状態の分布が存在しないということ。そのため行動$i$以外を選んだ方が良い様な場合が存在しない。
この時、リグレット0を達成できる。
簡単な問題(自明でなく局所観測可能な問題)
任意のパレート最適な行動のペア$\left(i_{1}, i_{2}\right) \in \mathcal{I}$に対して、
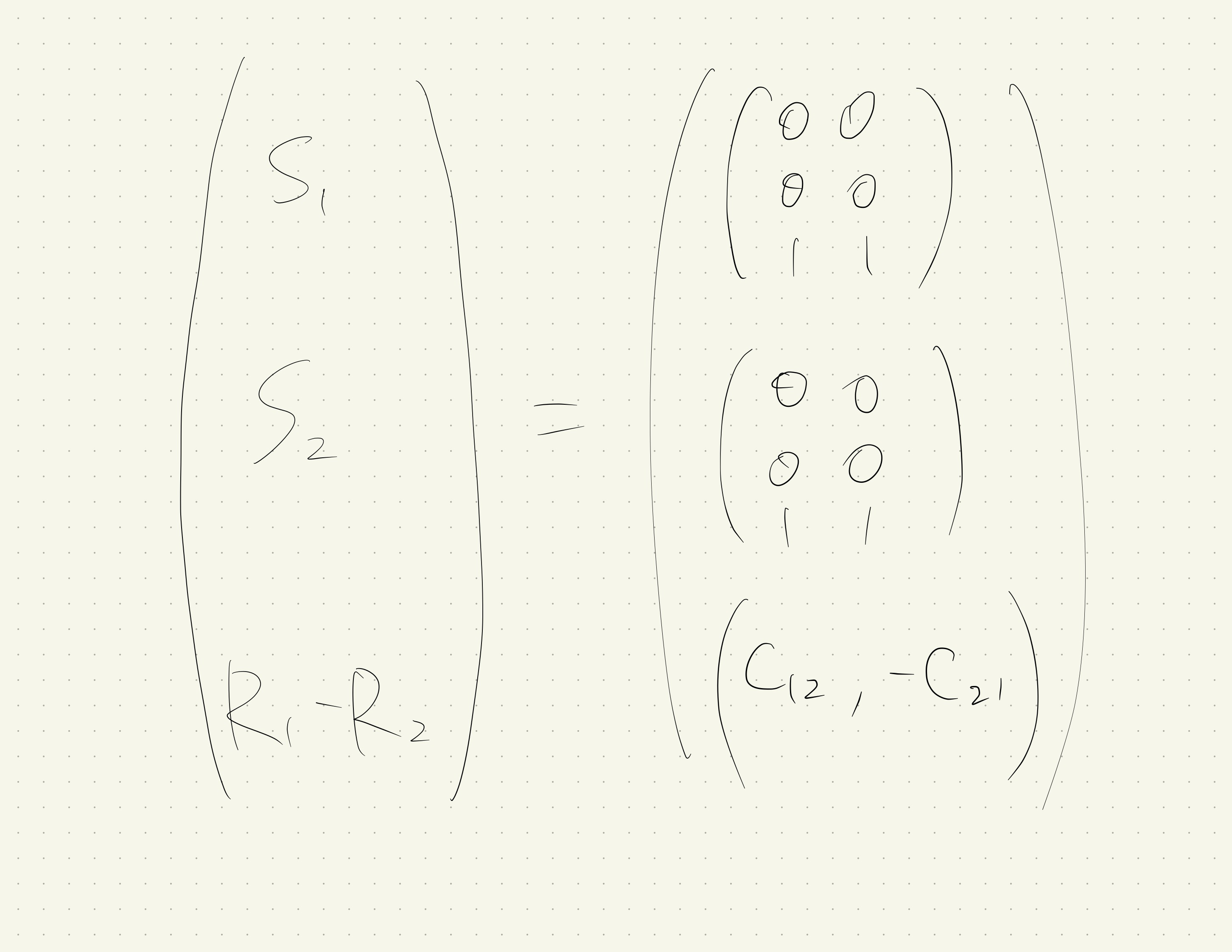
\operatorname{rank}\left(\begin{array}{c}{S_{i_{1}}} \\ {S_{i_{2}}} \\ {R_{i_{1}}-R_{i_{2}}}\end{array}\right)=\operatorname{rank}\left(\begin{array}{c}{S_{i_{1}}} \\ {S_{i_{2}}}\end{array}\right)
の時、局所観測可能であるという。
$S_{i_{1}}$は行x列が信号の種類x内部状態の種類
$S_{i_{2}}$も同様
$R_{i_{1}}-R_{i_{2}}$は 1x内部状態の種類。
なお、例9.3はこれに当てはまらない。
なぜなら、行動1、2のペアについて考えたとき、
となり、条件を満たさないので。
($R_1-R_2$を他の行で表すことができない)
局所観測可能な問題は行動$i_1$と行動$i_2$を十分な回数行うことで、期待値の優劣関係を判断できる(パレート最適な行動のみ行えば良い)
自明でなく、局所観測可能な時、簡単な問題という。
$\tilde{\mathrm{O}}\left(T^{1 / 2}\right)$の最悪時リグレットを達成可能で、かつそれ以上は改善不可能であることが知られている。
困難な問題(大域的観測可能な問題)
任意のパレート最適な行動のペア$\left(i_{1}, i_{2}\right) \in \mathcal{I}$に対して、
\operatorname{rank}\left(\begin{array}{c}{S_{1}} \\ {\vdots} \\ {S_{|\mathcal{I}|}} \\ {R_{i_{1}}-R_{i_{2}}}\end{array}\right)=\operatorname{rank}\left(\begin{array}{c}{S_{1}} \\ {\vdots} \\ {S_{|\mathcal{I}|}}\end{array}\right)
が成り立つ時、その問題を帯域的観測可能であるという。
この様な問題では、「全ての」行動を十分な回数行えば、行動$i_1$と$i_2$の期待値の優劣関係を判断することができる。(パレート最適でない行動も行う必要がある)
例9.3はこれに当てはまる。
例9.3で言えば、行動3を繰り返すことで内部状態1と2の比率がわかり、その結果最適な行動がわかる。
絶望的な問題
どの様な方策を取ったとしても、$p$によってはリグレット$\Omega(T)$となる。
pを定数とみなす問題依存リグレット
スキップ
9.3.3 部分観測問題の方策
部分観測問題はまだ研究途上の分野。
トンプソン抽出の応用が難しいらしい。
よくわからなかったです。
9.4 その他の拡張
組み合わせバンディット
行動の候補が$a \in \mathcal{A} \subset{0,1}^{d}$と言った組み合わせ的な量で表される設定。
一例として、行動の各構成要素に対応する報酬$\theta_j$の和、$\theta^{\top} a=\sum_{j=1}^{d} \theta_{j} a_{j}$が観測される設定などがある。
複数選択バンディット
- 各時刻に$K$個のスロットマシンのうち、L個を同時に選択し、それぞれに対応する報酬を観測する設定。
- ウェブサイト上に広告枠がL個あり、K個の広告から選び、どの広告がクリックされたかを観測する、という問題はこれにあたる
半バンディット
選択した行動の報酬だけでなくそれ以外の情報も部分的に観測される設定。
🤔複数選択バンディットはこれにあたる?
予算制約付きバンディット
各アーム$i$に選択コスト$c_i$が割り当てられていて、累計のコストが予算$B$を超えない様にアームを選択するという設定。
この問題では、コストパフォーマンス($\mu_i / c_i$)がいいアームを発見することが報酬の最大化に必要となる。
おしまい