はじめに
前回と前々回の記事では一般化加法モデルの中でも誤差が正規分布に従うケースを扱いました。一般化線形モデルと同様に一般化加法モデルも目的変数が指数型分布族に従うような場合にまで拡張することができます。今回の記事ではロジスティック回帰に一般化加法モデルを適用した「加法ロジスティック回帰」についてまとめます。
RとかPythonのライブラリを使えば簡単に実行できますが、できるだけ頼らずにどんな原理でパラメータの推定を行なっているか整理しようと思います。
一般化加法モデル (GAM)
$Y_1, \ldots,Y_n$を指数型分布族に従う独立な確率変数、$a$個の説明変数を$x_{i1},\ldots,x_{ia}$とします。
一般化線形モデル(GLM)では
g(\mu_i)=\beta_0 + \beta_1 x_{i1} + \cdots + \beta_a x_{ia}
のようなモデルを想定します。ここで、$\beta$は未知パラメータ、$g$はリンク関数 $E[Y_i]=\mu_i$です。
一方で、GAMでは非線形関数$f$を用いて
g(\mu_i)= f_1(x_{i1})+\cdots+f_a(x_{ia})
のようなモデルを想定します。そして、各$f(x)$は既知の$p$個の基底関数$b_{j}(x)$と未知のパラメータ$\beta_{j}$の線形結合として
f_{}(x)=\sum_{j=1}^{p}\beta_{j} b_{j}(x)
のように表現することができるとします。結局のところ、各説明変数を適当な基底関数を用いて変換した各$b(x)$を新たな説明変数と考えればGAMのモデルはGLMのモデルと同じ形になります。したがって、未知パラメータの推定は基本的には通常のGLMと同じ方法で行うことができます。
未知パラメータの推定
最尤推定
GLMと同様にGAMでも未知パラメータの推定は最尤法で行います。$\boldsymbol{Y}$を正準形の指数型分布族に従う互いに独立な目的変数のベクトル、$\boldsymbol{X}$をデザイン行列、$\boldsymbol{\beta}$を未知パラメータのベクトルとします。正準形の指数型分布族の確率密度関数は
f(y_i;\theta_i)=exp\{y_ib(\theta_i)+c(\theta_i)+d(y_i)\}
のように書くことができます。さらに、
E[Y_i]=\mu_i=-\frac{c'(\theta_i)}{b'(\theta_i)}
V[Y_i]=\frac{b''(\theta_i)c'(\theta_i)-c''(\theta_i)b'(\theta_i)}{b'(\theta_i)^3}
g(\mu_i)=\boldsymbol{X_i}\hspace{1pt}\boldsymbol{\beta}=\eta_i
となります。なお、$\boldsymbol{X_i}$は$\boldsymbol{X}$の$i$行目の行ベクトル、$g$はリンク関数です。$\boldsymbol{\beta}$に対する対数尤度関数$l(\boldsymbol{\beta})$は
l(\boldsymbol{\beta})=\sum_{i=1}^{n}\log f(y_i;\theta_i)=\sum_{i=1}^{n}\{y_ib(\theta_i)+c(\theta_i)+d(y_i)\}
となります。$l(\boldsymbol{\beta})$を最大にする$\boldsymbol{\beta}=\hat{\boldsymbol{\beta}}$が最尤推定量になりますが、解析的に求めることが難しい場合が多いため、Newton-Raphson法などを用いて数値的に解を求める必要があります。今回はNewton-Raphson法の一種であるスコア法を用いて$\boldsymbol{\beta}$の最尤推定値を求めます。スコア法では以下の推定方程式を用いて$\boldsymbol{\beta}$の推定値が収束するまで反復計算を行います。
\boldsymbol{B}^{[m-1]}\boldsymbol{\beta}^{[m]}=\boldsymbol{B}^{[m-1]}\boldsymbol{\beta}^{[m-1]}+\boldsymbol{U}^{[m-1]}\hspace{5pt}\cdots\hspace{5pt}(1)
ここで、$\boldsymbol{U}$はスコアベクトル、$\boldsymbol{B}$はFisher情報行列、上付きの添字$[m]$は$m$回目の反復で得られた値であることを示しています。$\boldsymbol{U}$及び$\boldsymbol{B}$の各成分は
U_j=\frac{\partial l(\boldsymbol{\beta})}{\partial \beta_j}=\sum_{i=1}^{n} \biggr\{ \frac{(y_i-\mu_i)}{V[Y_i]}\cdot x_{ij}\cdot \Bigr(\frac{\partial\mu_i}{\partial\eta_i} \Bigl) \biggr\}
B_{jk}=\sum_{i=1}^{n}\biggr\{\frac{x_{ij}x_{ik}}{V[Y_i]}\cdot \Bigr(\frac{\partial\mu_i}{\partial\eta_i} \Bigl)^2 \biggr\}
のように表されます。ここで、行列$\boldsymbol{W}$を
W_{ii}=\frac{1}{V[Y_i]}\cdot\Bigr(\frac{\partial\mu_i}{\partial\eta_i}\Bigl)^2
を$(i,i)$成分としてもつ対角行列とするとFisher情報行列$\boldsymbol{B}$は
\boldsymbol{B}=\boldsymbol{X}^T\boldsymbol{W}\boldsymbol{X}
と書き直すことができます。また、$(1)$式の右辺は
z_i=(y_i-\mu_i)\Bigr(\frac{\partial\mu_i}{\partial\eta_i}\Bigl)^{-1}+\hspace{3pt}\eta_i
を成分に持つベクトル$\boldsymbol{z}$を用いて
\boldsymbol{B}^{[m-1]}\boldsymbol{\beta}^{[m-1]}+\boldsymbol{U}^{[m-1]}=\boldsymbol{X}^T\boldsymbol{W}\boldsymbol{z}
と表現することができます。これらの計算には$(m-1)$回目の計算で得られた$\boldsymbol{\beta}^{[m-1]}$を用います。これを用いて$(1)$式を以下のように書き直すことができます。
\boldsymbol{X}^T\boldsymbol{W}\boldsymbol{X}\boldsymbol{\beta}^{[m]}=\boldsymbol{X}^T\boldsymbol{W}\boldsymbol{z}
これは正規方程式と同じ形をしているので、$\boldsymbol{\beta}$の最尤推定値は以下の二乗誤差を最小にする推定値になっています。
||\boldsymbol{M}\boldsymbol{z}-\boldsymbol{M}\boldsymbol{X}\boldsymbol{\beta}^{[m]}||^2
ここで、行列$\boldsymbol{M}$は$\boldsymbol{W}$の各成分の平方根をとった行列になります。したがって、$\boldsymbol{\beta}$の最尤推定値は目的変数を$\boldsymbol{M}\boldsymbol{z}$、デザイン行列を$\boldsymbol{M}\boldsymbol{X}$とした最小二乗法で推定することができます。ただし、$\boldsymbol{\beta}^{[m]}$を推定するのに必要な$\boldsymbol{W}$と$\boldsymbol{z}$の値は$\boldsymbol{\beta}^{[m-1]}$に依存しているため反復的に計算を行う必要があります。GAMでは単に上記の二乗誤差を最小にする推定値を求めるだけでは過学習の危険性が高いため、パラメータに対して適切なペナルティをかけることが必須になります。そこで、上記の二乗誤差にペナルティを追加した、
||\boldsymbol{M}\boldsymbol{z}-\boldsymbol{M}\boldsymbol{X}\boldsymbol{\beta}^{[m]}||^2 + \boldsymbol{\beta}^{[m]}\boldsymbol{S}\boldsymbol{\beta}^{[m]}
を最小化することにします。ここで、$\boldsymbol{S}$はペナルティ行列です。さらに、上記のペナルティ付き二乗誤差は$\boldsymbol{D}^T\boldsymbol{D}=\boldsymbol{S}$となるような行列を用いて、以下のようにペナルティ無しの二乗誤差として表現することができます。
\begin{Vmatrix}
\left[
\begin{array}{ll}
\boldsymbol{M} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{I}
\end{array}
\right]
\left[
\begin{array}{ll}
\boldsymbol{z} \\
\boldsymbol{0}
\end{array}
\right]-
\left[
\begin{array}{ll}
\boldsymbol{M} & \boldsymbol{0} \\
\boldsymbol{0} & \boldsymbol{I}
\end{array}
\right]
\left[
\begin{array}{ll}
\boldsymbol{X} \\
\boldsymbol{D}
\end{array}
\right]
\boldsymbol{\beta}^{[m]}
\end{Vmatrix}^2\hspace{5pt}\cdots\hspace{5pt}(2)
$\boldsymbol{I}$は単位行列です。これにより、GAMでの未知パラメータ$\boldsymbol{\beta}$の推定は以下の手順で行うことができます。
①:現在の$\boldsymbol{\mu}^{[m]}$と$\boldsymbol{\eta}^{[m]}$を用いて、$\boldsymbol{z}^{[m]}$と$\boldsymbol{W}^{[m]}$を計算する。
②:最小二乗法により式$(2)$を最小化する$\boldsymbol{\beta}^{[m+1]}$を得る。
③:$\boldsymbol{\eta}^{[m+1]}=\boldsymbol{X}\boldsymbol{\beta}^{[m+1]}$及び$\boldsymbol{\mu}^{[m+1]}=\boldsymbol{g}^{-1}(\boldsymbol{\eta}^{[m+1]})$に更新する。
この計算を$\boldsymbol{\beta}$の推定値が収束するまで繰り返すことで未知パラメータ最尤推定値を得ることができます。この方法はpenalized iteratively re-weighted least squares (P-IRLS)と呼ばれています。計算の初期値には$\mu_{i}^{[0]}=y_i$及び$\eta_{i}^{[0]}=g(\mu_{i}^{[0]})$を設定することが多いです。ただし、$\eta_{i}^{[0]}$が発散しないように初期値を調整する必要があります。
ロジスティック回帰の場合
ロジスティック回帰の場合、目的変数$Y_i$はそれぞれ独立にベルヌーイ分布$B(1, \theta_i)$に従う{$0, 1$}の2値を取る確率変数です。期待値は$E[Y_i]=\mu_i=\theta_i$、分散は$V[Y_i]=\theta_i(1-\theta_i)$となります。リンク関数にはロジットリンク関数を用いて
g(\mu_i)=\log \Bigr(\frac{\mu_i}{1-\mu_i} \Bigl)=\boldsymbol{X}_i\hspace{1pt}\boldsymbol{\beta}=\eta_i
のようなモデルの未知パラメータ$\boldsymbol{\beta}$を推定します。$\eta_i$が既知のとして逆関数を考えると
\mu_i=\frac{e^{\eta_i}}{1+e^{\eta_i}}
のように$\mu_i$を求めることができます。また、数値計算に必要な$\boldsymbol{W}$及び$\boldsymbol{z}$の各成分は
W_{ii}=\frac{1}{V[Y_i]}\cdot\Bigr(\frac{\partial\mu_i}{\partial\eta_i}\Bigl)^2=\mu_i(1-\mu_i)
z_i=(y_i-\mu_i)\Bigr(\frac{\partial\mu_i}{\partial\eta_i}\Bigl)^{-1}+\hspace{3pt}\eta_i=\frac{y_i-\mu_i}{\mu_i(1-\mu_i)}+\eta_i
のようになります。
加法ロジスティック回帰 (説明変数が1つ)
以下のようなデータを用いて加法ロジスティック回帰による2値分類を行なってみます。$x$が説明変数、$y$が$0, 1$の2値の値をとる目的変数になっています。
> head(test_data)
# A tibble: 6 x 2
x y
<dbl> <int>
1 -5 1
2 -4.90 1
3 -4.80 1
4 -4.70 1
5 -4.60 0
6 -4.49 1

普通のロジスティック回帰
まずは比較のために通常のロジスティック回帰のパラメータ推定値を確認し、予測確率及びPartial residualをplotしてみます。
> # ロジスティック回帰実行
> model_glm <- glm(y ~ x, data = test_data, family = binomial(link = "logit"))
> model_glm$coefficients
(Intercept) x
-0.08126824 -0.08502768
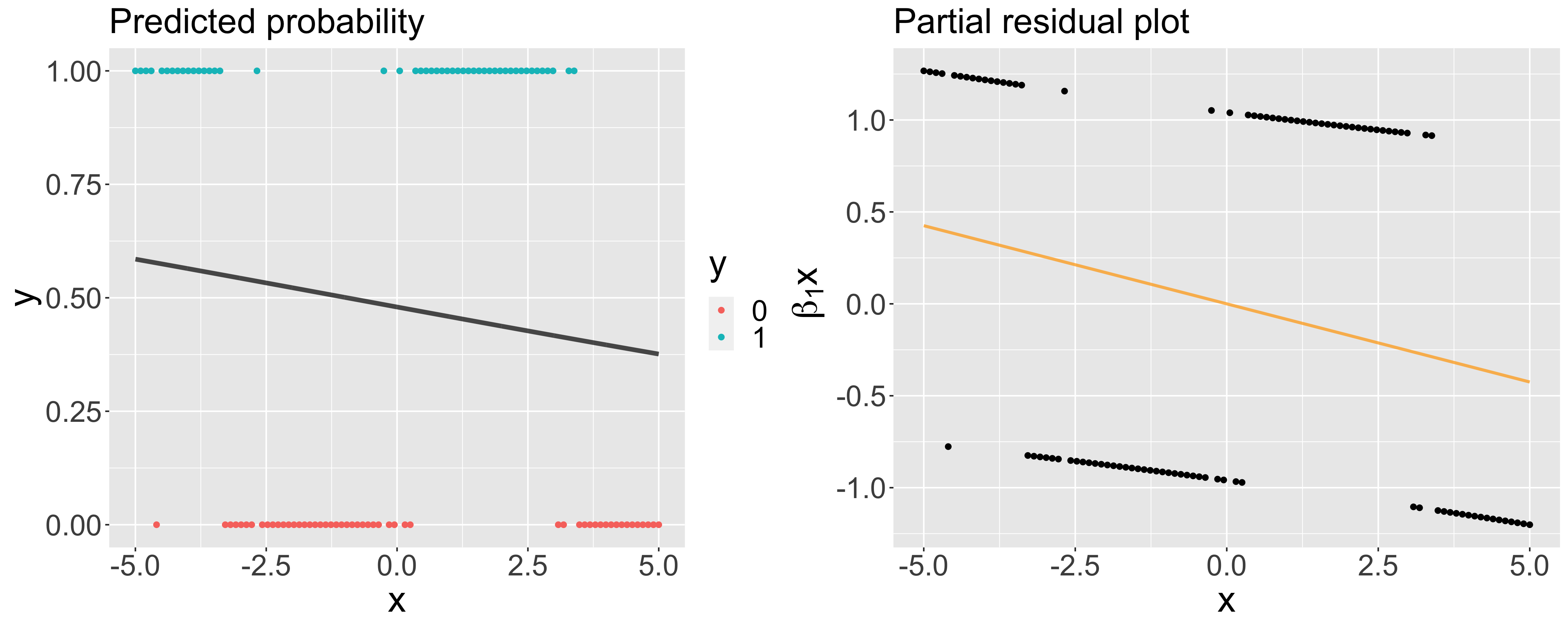
上のplotを確認してみると普通のロジスティック回帰ではあまりデータを上手く表現できていないことがわかります。分類結果の混同行列を以下に示しています。Accuracyは0.45でした。
加法ロジスティック回帰
加法ロジスティック回帰を用いて分類を行います。今回は基底関数にはB-spline基底を用いることにします。まずは、説明変数をB-spline基底で変換したデザイン行列$\boldsymbol{X}$とペナルティ行列$\boldsymbol{S}$を準備します。このあたりの詳細に関しては前回の記事を参照してください。
# データ
x <- test_data$x
y <- test_data$y
N <- nrow(test_data)
# 平滑化パラメータ
lambda <- 2.5
# ノットベクトル
knot <- c(-9.3042857,-7.8728571,-6.4414286,-5.0100000,-3.5785714,-2.1471429,-0.7157143,
0.7157143,2.1471429,3.5785714,5.0100000,6.4414286,7.8728571,9.3042857)
# デザイン行列の作成
X <- splineDesign(knot, x)
QR <- qr(t(matrix(1, nrow = 1, ncol = N) %*% X))
Z <- qr.Q(QR, complete = TRUE)[, 2:ncol(X)]
X <- X %*% Z
X <- cbind(1, X)
# ペナルティ行列(2階差分ペナルティ)
S <- crossprod(diff(diag(length(knot)-4), differences = 2))
S <- (t(Z) %*% S %*% Z)/norm(S)
S <- lambda * S
S <- cbind(0, S)
S <- rbind(0, S)
必要な行列を準備することができたので、実際に未知パラメータを最尤推定します。平滑化パラメータの値はとりあえず$2.5$に設定しています。反復計算の回数は10回にしていますが、これくらいかなって感覚で決めているので収束しているかちゃんと確認しましょう。
# 初期値
mu <- y*0.8 + 0.1
eta <- log(mu/(1-mu))
# P-IRLS
for (i in 1:10){
# ①ベクトルzの計算
z <- ((y-mu)/(mu*(1-mu))) + eta
z <- matrix(z)
# ①行列Wの計算
W <- mu*(1-mu)
W <- diag(W)
# ②未知パラメータの推定
M <- sqrt(W)
SVD <- svd(S)
D <- SVD$u %*% diag(sqrt(SVD$d)) %*% t(SVD$v)
XD <- rbind(X, D)
z0 <- rbind(z, matrix(0, ncol = 1, nrow = nrow(D)))
WI <- rbind(cbind(M, matrix(0, ncol = nrow(D), nrow = nrow(M))),
cbind(matrix(0, ncol = ncol(M), nrow = nrow(D)), diag(1, nrow = nrow(D), ncol = nrow(D))))
QR <- qr(WI%*%XD)
beta <- backsolve(qr.R(QR), qr.qty(QR, WI%*%z0))
# ③eta, muの更新
eta <- as.numeric(X%*%beta)
mu <- 1/(1+exp(-1*eta))
}
> as.numeric(beta)
[1] -0.2565651 2.7848339 -2.2172244 -5.8924840 -5.1985421 -0.7790684 0.6469540 -3.3073689 -7.7851337 -12.2097671
パラメータ推定値を得ることができたので、予測確率及びPartial residualをplotしてみます。

明らかに普通のロジスティック回帰よりもデータを上手く表現できていることがわかります。混同行列を確認してみるとAccuracyが0.9まで改善していることがわかります。
実際には平滑化パラメータはクロスバリデーションで適切な値を選択する必要があります。平滑化パラメータの値が大きくなるほどモデルは単純になっていきます。
加法ロジスティック回帰 (説明変数が2つ)
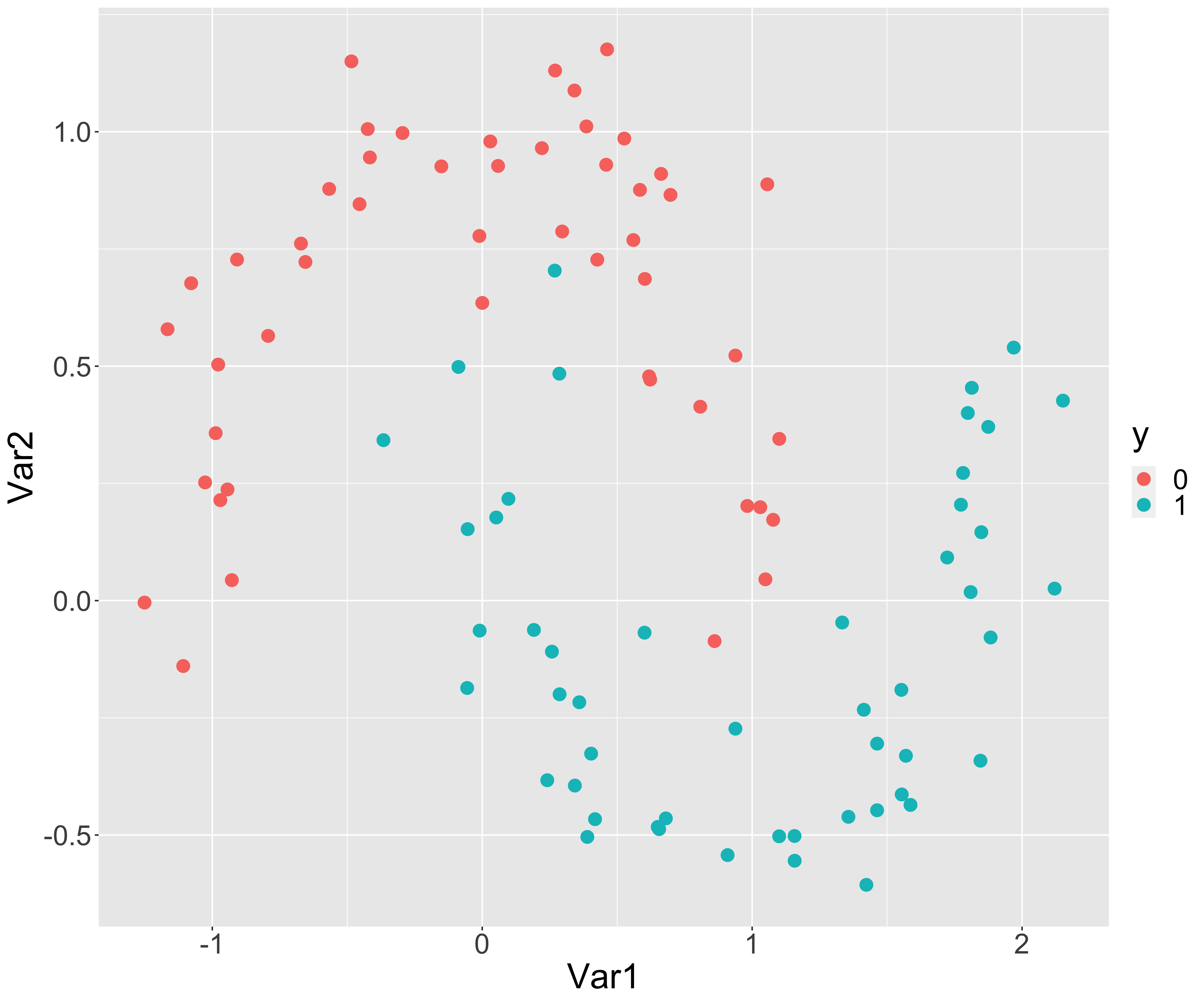
例として説明変数が2つある場合も見てみます。以下のような$0, 1$の$2$値を取る目的変数$y$と2つの説明変数Var1, Var2を持つデータに対してロジスティック回帰による2値分類を行います。
> head(test_data)
# A tibble: 6 x 3
Var1 Var2 y
<dbl> <dbl> <int>
1 -0.793 0.565 0
2 -0.485 1.15 0
3 1.36 -0.461 1
4 0.258 -0.109 1
5 2.15 0.427 1
6 0.418 -0.466 1
普通のロジスティック回帰
まずは普通のロジスティック回帰を行なって、分類の境界線を書いてみます。
> # ロジスティック回帰実行
> model_glm <- glm(y ~ Var1 + Var2, data = test_data, family = binomial(link = "logit"))
> model_glm$coefficients
(Intercept) Var1 Var2
0.6071223 1.3283576 -4.7405215

上のグラフのように普通のロジスティック回帰では分類境界は直線になるため、上手くデータの特徴を捉えた分類が行えない場合があります。まあ、今回の例では直線でも割と上手く分類できているような気もしますが。
加法ロジスティック回帰
1変数の時と同じようにB-spline基底を用いて加法ロジスティック回帰を行います。まずは、説明変数をB-spline基底で変換したデザイン行列$\boldsymbol{X}$とペナルティ行列$\boldsymbol{S}$を準備しましょう。
# データ
var1 <- test_data$Var1
var2 <- test_data$Var2
y <- test_data$y
N <- nrow(test_data)
# 平滑化パラメータ
lambda1 <- 1
lambda2 <- 2
# ノットベクトル
knot1 <- c(-2.7156358,-2.2285810,-1.7415261,-1.2544713,-0.7674164,-0.2803616,0.2066933,
0.6937481,1.1808030,1.6678578,2.1549126,2.6419675,3.1290223,3.6160772)
knot2 <- c(-1.37318817,-1.11812781,-0.86306744,-0.60800707,-0.35294671,-0.09788634,0.15717402,
0.41223439,0.66729475,0.92235512,1.17741548,1.43247585,1.68753621,1.94259658)
# デザイン行列の作成
X1 <- splineDesign(knot1, var1)
QR1 <- qr(t(matrix(1, nrow = 1, ncol = N) %*% X1))
Z1 <- qr.Q(QR1, complete = TRUE)[, 2:ncol(X1)]
X1 <- X1 %*% Z1
X2 <- splineDesign(knot2, var2)
QR2 <- qr(t(matrix(1, nrow = 1, ncol = N) %*% X2))
Z2 <- qr.Q(QR2, complete = TRUE)[, 2:ncol(X2)]
X2 <- X2 %*% Z2
X <- cbind(1, X1, X2)
# ペナルティ行列
S1 <- crossprod(diff(diag(length(knot1)-4), differences = 2))
S1 <- (t(Z1) %*% S1 %*% Z1)/norm(S1)
S1 <- lambda1 * S1
S2 <- crossprod(diff(diag(length(knot2)-4), differences = 2))
S2 <- (t(Z2) %*% S2 %*% Z2)/norm(S2)
S2 <- lambda2 * S2
S <- rbind(cbind(S1, matrix(0, ncol = ncol(S2), nrow = nrow(S1))),
cbind(matrix(0, ncol = ncol(S1), nrow = nrow(S2)), S2))
S <- cbind(0, S)
S <- rbind(0, S)
パラメータの推定の計算については説明変数が1つの場合と全く同じです。推定されたパラメータの値を以下に示します。
> as.numeric(beta)
[1] 0.1440492 -5.7028720 1.4627238 6.3826616 9.7494472 4.9018292 1.8276606 6.3164296 10.0046231
[10] 14.2315375 5.8777856 0.6895253 -2.0757022 -4.1050686 -5.0077996 -6.9177117 -10.2949817 -10.9852868
[19] -12.7342627
とはいえパラメータの推定値を見ても何が何だかよくわからないので、分類境界とPartial residualをグラフにしてみましょう。
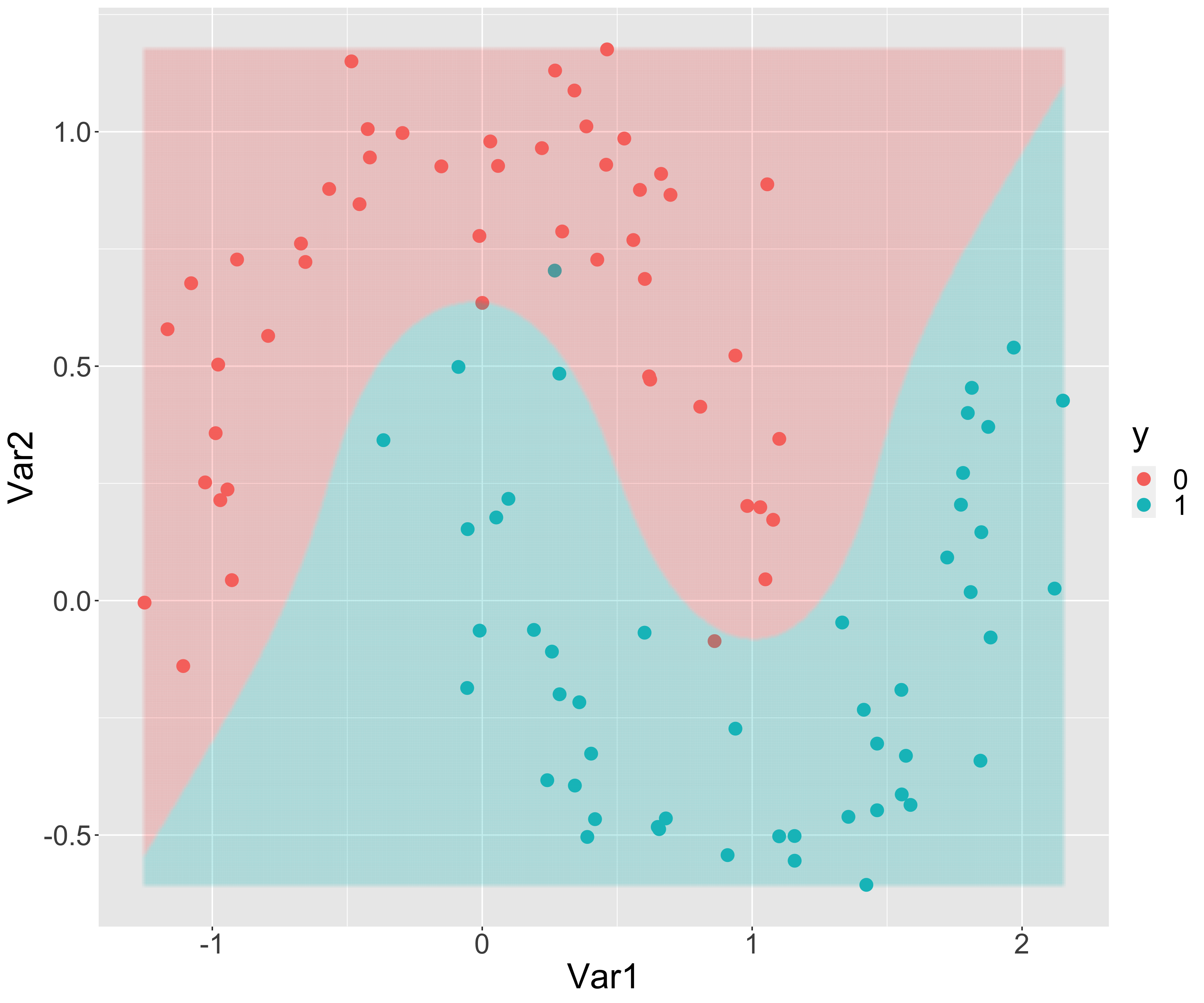

加法ロジスティック回帰を用いることで曲線の分類境界を描くことができます。Partial residual plotを見てもモデルの当てはまりはかなり良さそうです。ただし、過学習には十分注意を払う必要があります。モデルの解釈性に関しては、Partial residual plotを確認することで各説明変数によって対数オッズがどのように変化しているかが分かるため解釈性はかなり高いと思います。このようなデータの分類には色々な方法がありますが、解釈性の高いモデルが得られることは加法ロジスティック回帰の利点の一つだと思います。
mgcvで加法ロジスティック回帰
Rのmgcvパッケージを用いれば簡単に加法ロジスティック回帰を行えます。先程の2変数の場合の加法ロジスティック回帰と同じパラメータ推定値が得られます。
model_gam <- gam(
y ~ s(Var1, bs = "ps", k = 10, sp = 1) + s(Var2, bs = "ps", k = 10, sp = 2),
data = test_data,
family = binomial(link = logit)
)
> model_gam$coefficients
(Intercept) s(Var1).1 s(Var1).2 s(Var1).3 s(Var1).4 s(Var1).5 s(Var1).6
0.1440492 -5.7028719 1.4627237 6.3826615 9.7494471 4.9018293 1.8276608
s(Var1).7 s(Var1).8 s(Var1).9 s(Var2).1 s(Var2).2 s(Var2).3 s(Var2).4
6.3164295 10.0046232 14.2315376 5.8777857 0.6895253 -2.0757022 -4.1050686
s(Var2).5 s(Var2).6 s(Var2).7 s(Var2).8 s(Var2).9
-5.0077996 -6.9177117 -10.2949818 -10.9852868 -12.7342627
参考文献
- Generalized Additive Models:an introduction with R
- Annette J.Dobson 一般化線形モデル入門
記事内で使用したプログラム

