はじめに
一般化加法モデルを用いた回帰分析について勉強したのでまとめておくことにします。基礎的な線形回帰の知識(最小二乗法、デザイン行列、正規方程式とか)があることは前提としています。
一般化加法モデル (GAM)
一般化加法モデル(Generalized Additive Model: GAM)の導入として、応答変数$y$と一つの説明変数$x$の関係性を表現するようなモデルを考えることにします。いま、応答変数$y$と説明変数$x$の以下のグラフに示すようなデータが得られているとします。

グラフから応答変数$y$と説明変数$x$の間には明らかに非線形な関係性があることが見て取れます。このような場合、通常の線形回帰では応答変数$y$と説明変数$x$の関係を十分に表現することはできません。このような場合は、例えば多項式回帰・サポートベクター回帰・ニューラルネットワークなど、非線形な関数を学習できる手法を適用することになります。今回取り上げるGAMも応答変数と説明変数の非線形な関係を学習することができる統計モデルの一つです。
GAMでは応答変数$y$と説明変数$x$の関係を以下のようにモデル化します。1
y_i=f(x_i)+\epsilon_i, \hspace{5pt}\epsilon_i\tilde{}\hspace{2pt}N(0, \sigma^2)\hspace{20pt} (i=1, 2, \ldots, n)
$f(x)$は説明変数$x$の関数でなので、$f(x)$を非線形な関数とすればこのモデルを用いて応答変数と説明変数の非線形な関係を表現することができそうです。しかし、このままでは「$f(x)$は説明変数$x$の関数」という条件しかないのでデータからどのように$f(x)$を推定すれば良いのかわかりません。そこで、$f(x)$を$p$個の基底関数$b_j(x)$と未知のパラメータ$\beta_j$の線形結合として以下のように表現することができるとします。
f(x)=\sum_{j=1}^{p}\beta_j b_j(x)
$f(x)$を上記のように表現することで、応答変数$y$と説明変数$x$の関係を以下のように書き直すことができます。
y_i=\sum_{j=1}^{p}\beta_j b_j(x_i)+\epsilon_i, \hspace{5pt}\epsilon_i\tilde{}\hspace{2pt}N(0, \sigma^2)\hspace{20pt} (i=1, 2, \ldots, n)
このように基底関数を用いて表現することで「$f(x)$を推定する」という問題を「$p$個の未知パラメータ$\beta_j$を推定する」という問題に置き換えることができました。しかも、上記の式は$b_j(x_i)$を説明変数とする線形回帰になっているので未知パラメータ$\beta_j$は最小二乗法で求めることができそうです。
最小二乗法でパラメータの推定を行う場合はデザイン行列$\boldsymbol{X}$を基底関数$b_j(x)$を用いて、
\boldsymbol{X} =
\left(
\begin{matrix}
b_{1}(x_1) & b_{2}(x_1) & \cdots & b_{p}(x_1) \\\
b_{1}(x_2) & b_{2}(x_2) & \cdots & b_{p}(x_2) \\\
\vdots & \vdots & \ddots &\vdots \\\
b_{1}(x_n) & b_{2}(x_n) & \cdots & b_{p}(x_n)
\end{matrix}
\right)
のように構成します。すると、以下のように正規方程式を解くことでパラメータの最小二乗推定量$\hat{\boldsymbol{\beta}}$を求めることができます。
\hat{\boldsymbol{\beta}}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}
予測値$\hat{\boldsymbol{y}}$はパラメータ推定値$\hat{\boldsymbol{\beta}}$とデザイン行列$\boldsymbol{X}$を用いて以下のように算出できます。
\hat{\boldsymbol{y}}=\boldsymbol{X}\hat{\boldsymbol{\beta}}
当然ですが、基底関数は分析を行う前に自分で選択しなければなりません。GAMでは「基底関数$b_j(x)$を決める」→「デザイン行列$X$を構成する」→「正規方程式を解いてパラメータ推定値$\hat{\boldsymbol{\beta}}$を得る」という流れで回帰分析をおこないます。
多項式基底
GAMの簡単な例として、以下のような$(p+1)$個の基底関数を考えます。
b_j(x)=x^j \hspace{10pt} (j=0, 1,\ldots, p)
このような基底関数を$p$次の多項式基底と呼びます。見てわかる通り、$p$次の多項式基底を用いたGAMは$p$次の多項式回帰と全く同じになります。この場合のデザイン行列$\boldsymbol{X}$は以下のようになります。
\boldsymbol{X} =
\left(
\begin{matrix}
1 & x_{1} & x_{1}^2 & \cdots & x_{1}^p \\\
1 & x_{2} & x_{2}^2 & \cdots & x_{2}^p \\\
\vdots & \vdots & \vdots & \ddots & \vdots \\\
1 & x_{n} & x_{n}^2 & \cdots & x_{n}^p
\end{matrix}
\right)
それでは$p=9$として、$10$個の基底関数を用いた回帰分析を実際に行ってみましょう。

なかなか良い感じに曲線を引くことができている気がします。以下のグラフは基底関数とパラメータ推定値の積をプロットしたものです。10個の基底関数すべてをプロットすると多いので、ここでは$\beta_0b_0(x),\ldots,\beta_5b_5(x)$の6個を示しています。以下のグラフに示した関数(と残り4個で計10個の関数)をすべて足し合わせることで最終的に上記のグラフに示したような回帰曲線を得ることができます。
このように基底関数の線形結合によって一つの関数を作ろうというのがGAMによる回帰分析の考え方です。一つ一つの基底関数はシンプルな形をしていても、その線形結合はなかなか複雑な形を表現できていることがわかります。
また、多項式基底で$p=1$とすれば普通の単回帰モデル$y_i=\beta_0+\beta_1x+\epsilon_i$になることがわかります。このように考えると、GAMは線形回帰を含むより一般的なモデルであると言えます。基底関数を変えることで様々な回帰分析を行うことができそうですね。
区分多項式基底
区分多項式とは?
多項式基底を用いたGAMでなかなかに良い感じにデータにフィットする曲線を引くことができました。しかし、多項式基底には過学習しやすかったり、データ範囲外では回帰曲線が大きく変動してしまったりといった欠点もあります。
このような欠点を回避するために出来るだけ低次の多項式で回帰分析を行いたいです。しかし、次数が低いと柔軟な曲線を引くことができません。どのように対応すれば良いでしょうか?
この問題を解決するために、以下のグラフのように$x$軸でデータを分割することを考えます。青の点線の位置で$S1, S2, S3, S4$の4つの区分に分割しましょう。分割位置は$x=6$, $x=12$, $x=18$です。また、この分割位置のことをknot (ノット)と呼びます。
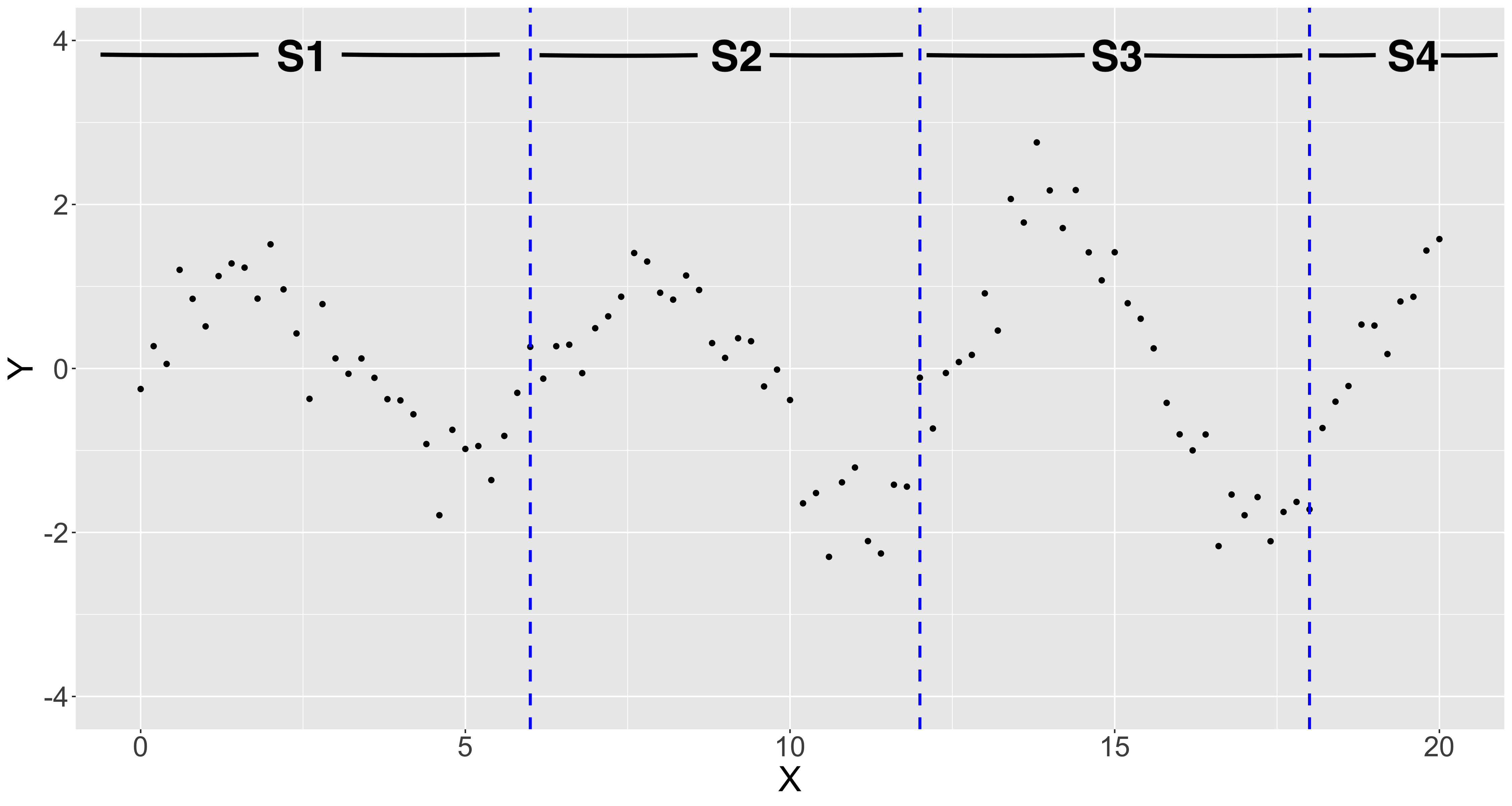
データ全体を一つの多項式で表現するには次数の高い多項式が必要ですが、データを分割すると各区分内は次数の低い多項式で表現することができそうです。そこで、以下のように各区分をそれぞれ異なるp次多項式で回帰することを考えます。これを区分多項式と呼びます。
\displaylines{S1: y_i=\beta_{10}+\beta_{11}x_i+\beta_{12}x_i^2+\cdots+\beta_{1p}x_i^p\\\
S2: y_i=\beta_{20}+\beta_{21}x_i+\beta_{22}x_i^2+\cdots+\beta_{2p}x_i^p \\\
S3: y_i=\beta_{30}+\beta_{31}x_i+\beta_{32}x_i^2+\cdots+\beta_{3p}x_i^p \\\
S4: y_i=\beta_{40}+\beta_{41}x_i+\beta_{42}x_i^2+\cdots+\beta_{4p}x_i^p }
区分が増えるほど推定するパラメータは増えてしまいますが、多項式の次数は低く抑えることができます。各区分ごとに別々に正規方程式を解いてパラメータ推定値を求めても良いのですが、今回は基底関数を上手く作ることで一度の計算ですべてのパラメータを求めるようにしましょう。
###区分多項式を基底関数を用いて表現する
K個のknotを$a_1, a_2, \ldots, a_K$とします。また、$i<j$ならば$a_i<a_j$となるようにknotは値の小さい順に並べて、同じ値は無いようにします。knotで分割した各区分で$p$次多項式を用いた回帰分析を行うとき、推定すべきパラメータは$(K+1)\times(p+1)$個です。そこで、以下のように基底関数を定義すると一度の計算ですべてのパラメータ推定値を得ることができます。
b_{00}(x)=1, \hspace{5pt}
b_{10}(x)= \left\{
\begin{array}{ll}
1 & (a_1 \leq x < a_2) \\
0 & (otherwise)
\end{array}
\right.,\hspace{5pt}
b_{20}(x)= \left\{
\begin{array}{ll}
1 & (a_2 \leq x < a_3) \\
0 & (otherwise)
\end{array}
\right.,\cdots,
b_{K0}(x)= \left\{
\begin{array}{ll}
1 & (a_K \leq x) \\
0 & (otherwise)
\end{array}
\right.
b_{0j}(x)=x^j, \hspace{5pt}
b_{1j}(x)= \left\{
\begin{array}{ll}
1 & (a_1 \leq x < a_2) \\
x^j & (otherwise)
\end{array}
\right.,\hspace{5pt}
b_{2j}(x)= \left\{
\begin{array}{ll}
1 & (a_2 \leq x < a_3) \\
x^j & (otherwise)
\end{array}
\right.,\cdots,
b_{Kj}(x)= \left\{
\begin{array}{ll}
1 & (a_K \leq x) \\
x^j & (otherwise)
\end{array}
\right.
(j=1, 2, \ldots, p)
デザイン行列$\boldsymbol{X}$は、$\boldsymbol{b_j}(x)=(b_{0j}(x)\hspace{6pt}b_{1j}(x)\hspace{6pt}\cdots\hspace{6pt}b_{Kj}(x))\hspace{8pt}(j=0, 1, \ldots, p)$と置くと以下のように構成することができます。
\boldsymbol{X} =
\left(
\begin{matrix}
\boldsymbol{b_0}(x_1) & \boldsymbol{b_1}(x_1) & \cdots & \boldsymbol{b_p}(x_1) \\\
\boldsymbol{b_0}(x_2) & \boldsymbol{b_1}(x_2) & \cdots & \boldsymbol{b_p}(x_2) \\\
\vdots & \vdots & \ddots & \vdots \\\
\boldsymbol{b_0}(x_n) & \boldsymbol{b_1}(x_n) & \cdots & \boldsymbol{b_p}(x_n)
\end{matrix}
\right)
そこそこ複雑な形になってしまいましたが、なんとか我慢してこのデザイン行列でパラメータ推定値を計算して$p=3$の回帰曲線を書いてみることにします。
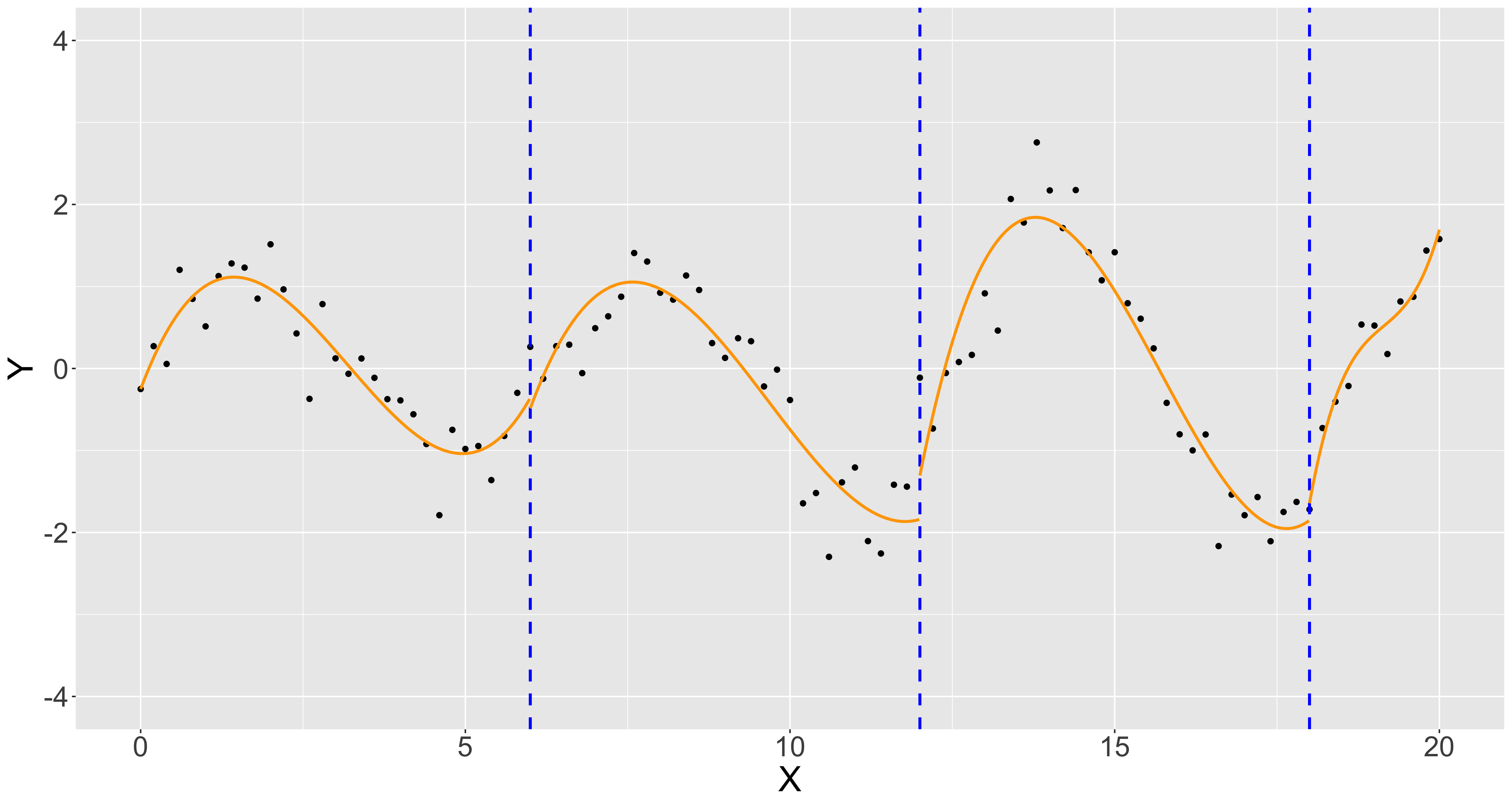
グラフを見てみると、各区分で使用しているのは3次多項式にも関わらず、回帰曲線全体としてはデータの特徴をよく表現できていることがわかります。区分多項式を用いることで多項式の次数は低く抑えつつ、柔軟な曲線を描くことができました。
スプライン基底
スプラインとは?
区分多項式を用いたGAMの不満なところは、各区分の回帰曲線がつながっていないところです。そこで、各区分の回帰曲線がつながるような曲線を描くことを考えます。しかも、単につながるだけではなくて滑らかにつながるようにします。どれくらい滑らかかと言うと、各区分を$p$次多項式で回帰分析を行った場合、各区分点 (knotの位置)で$p-1$次導関数が連続になるようにします。このような制約を入れた区分多項式のことを$p$次スプラインと呼びます。
スプラインを基底関数を用いて表現する
区分多項式と同様にK個のknotを$a_1, a_2, \ldots, a_K$とします。$p$次スプラインは$(K+p+1)$個の基底関数を用いて以下のように表現することができます。
\displaylines{b_j(x)=x^j\hspace{48pt}(j=0, 1, \ldots, p)\\
b_{p+k}(x)=(x-a_k)_+^p\hspace{15pt}(k=1, 2, \ldots, K)}
ここで、$(x)_+^p=\{max(0,x)\}^p$と定義します。$p$次スプラインでは関数が連続になるような制約条件を課したことで、未知パラメータの数が区分多項式よりも少なくなり$(K+p+1)$個になっています。
デザイン行列$\boldsymbol{X}$は以下のように構成することができます。
\boldsymbol{X} =
\left(
\begin{matrix}
b_0(x_1) & b_1(x_1) & \cdots & b_p(x_1) & b_{p+1}(x_1) & b_{p+2}(x_1) & \cdots & b_{p+K}(x_1) \\\
b_0(x_2) & b_1(x_2) & \cdots & b_p(x_2) & b_{p+1}(x_2) & b_{p+2}(x_2) & \cdots & b_{p+K}(x_2) \\\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\\
b_0(x_n) & b_1(x_n) & \cdots & b_p(x_n) & b_{p+1}(x_n) & b_{p+2}(x_n) & \cdots & b_{p+K}(x_n)
\end{matrix}
\right)
それでは準備が整ったので、例として3次スプライン基底(cubic spline)を用いたGAMで回帰曲線を書いてみましょう。knotは区分多項式の時と同様に$x=6$, $12$, $18$とします。

確かに回帰曲線は滑らかにつながっているように見えますが、なんだか平坦な曲線になってしまいました。これは関数が連続になるような制約条件を課して自由に選べるパラメータの数が減ったためだと思います。
この問題を解決するには4次スプラインや5次スプラインなどさらに次数の高いスプライン基底を用いるか、knotの数を増やす必要があります。ここではあまり次数の高い多項式は使いたくないので、3次スプライン基底のままでknotの数を増やすことにします。思い切ってknotを$x=2$, $4$, $6$, $8$, $10$, $12$, $14$, $16$, $18$の9個に増やしてみましょう。

knotの数を増やすことで今度はデータの特徴をよく表現した曲線を描くことができました。knotの数もスプライン基底を用いたGAMを行う際には考慮すべき重要なパラメータであることがわかりますね。
3次自然スプライン基底
3次自然スプラインとは?
先ほど行った3次スプライン基底を用いたGAMの問題点を確認するために、回帰曲線をデータの範囲外まで伸ばしたグラフを描いてみます。

上のグラフではデータに含まれている$x$軸の範囲は0~20ですが、そこから$\pm5$の範囲まで回帰曲線を伸ばしています。データの範囲内ではデータによくフィットした曲線になっていましたが、データの範囲から離れるほど大きく値が変化してしまっていることがわかります。そもそも回帰曲線をデータの範囲外に適応するのは難しいのですが、値が大きく変化する傾向をなんとか緩和することはできないでしょうか?
そこで、3次スプラインにさらに制約条件を追加することにします。データの両端を$x_0, x_n$とした時に、
f''(x_0)=f''(x_n)=0
という条件を入れましょう。関数$f$で3次スプライン基底を用いた回帰曲線全体を表しています。このようにデータの両端での2次導関数の値を0とする制約条件を入れた3次スプラインを3次自然スプラインと呼びます。この制約条件によりデータの範囲の外側に線形制約が課されたことになるため、値が大きく変化する問題を緩和することができそうです。
3次自然スプラインを基底関数を用いて表現する
これまでと同様にK個のknotを$a_1, a_2, \ldots, a_K$とします。3次自然スプライン基底は以下のように表すことができるようです。
\displaylines{b_1(x)=1 \\
b_2(x)=x \\
b_{2+m}(x)=d_m(x)-d_{K-1}(x)\hspace{10pt}(m=1, 2, \ldots, K-2)}
ここで、$d_m(x)$は以下のように定義される関数です。
d_m(x)=\frac{(x-a_m)_+^3-(x-a_K)_+^3}{a_K-a_m}
3次スプラインにさらに制約条件を追加したことで、基底関数の数はknotと同じ数であるK個まで減りました。当然ですが、推定すべき未知パラメータの数もK個です。
デザイン行列$\boldsymbol{X}$は以下のように構成することができます。
\boldsymbol{X} =
\left(
\begin{matrix}
b_1(x_1) & b_2(x_1) & \cdots & b_K(x_1) \\\
b_1(x_2) & b_2(x_2) & \cdots & b_K(x_2) \\\
\vdots & \vdots & \ddots & \vdots \\\
b_1(x_n) & b_2(x_n) & \cdots & b_K(x_n)
\end{matrix}
\right)
それでは3次自然スプライン基底(natural cubic spline)を用いたGAMで回帰曲線を描いてみましょう。knotは3次スプラインで上手くいった$x=2$, $4$, $6$, $8$, $10$, $12$, $14$, $16$, $18$の9個にします。

先ほどの3次スプライン基底と今回の3次自然スプライン基底では回帰曲線も少し変化していることがわかります。3次自然スプライン基底では左端の方で少し当てはまりが悪くなっているように見えます。当てはまりを良くしたい場合はより柔軟な曲線が描けるようにknotを追加したり、knotの位置を変えたりと適切な回帰曲線が得られるようにknotを上手く調整してあげる必要があります。
3次自然スプライン基底関数は以下のようになっています。基底関数とパラメータ推定値の積をプロットしているので、以下のグラフの関数を全て足すことで回帰曲線が作られています。
また、3次自然スプラインを導入した目的はデータ範囲外で値が大きく変化しないようにすることだったので、回帰曲線をデータ範囲外まで伸ばしたグラフを描いてみます。

上のグラフでは3次スプライン基底と3次自然スプライン基底を用いたGAMによる回帰曲線を比較しています。明らかに3次自然スプライン基底を用いた方がデータ範囲外での曲線の変化が小さいことがわかります。
ペナルティ付き最小二乗法
knotの影響
3次自然スプライン基底を用いたGAMでknotの数や位置がどのように回帰曲線に影響するか見てみることにします。以下のグラフでは青の点線がknotの位置、$K$でknotの数を示しています。
knotが少ないと適合不足、knotが多いと今度は過剰適合しているような曲線になっています。また、knotの位置によっても曲線の形状が大きく変わることがわかります。上のグラフはかなり極端な例ではありますが、knotの選択はとても重要な要素になっていることがわかると思います。
ペナルティ付き最小二乗法
ここで、今までとは少し異なる方法で曲線の形を制御する方法を考えることにします。これまでのGAMでは基底関数を決めた後、最小二乗法を使って以下の二乗誤差を最小化する$f(x)$を求めていました。
\sum_{i=1}^{n}\{y_i-f(x_i)\}^2
ここにペナルティ項を加えて、以下のようなペナルティ付き二乗誤差を最小化するような$f(x)$を求めることにします。
\sum_{i=1}^{n}\{y_i-f(x_i)\}^2+\lambda\int_{x_0}^{x_n}\{f''(x)\}^2dx
追加した項をここではペナルティ項と呼んでいますが、Ridge回帰やLasso回帰で使用するような正則化項と同じ働きをする項です。$f(x)$の二次導関数の2乗を説明変数の範囲全体で積分しているので、ペナルティ項は曲線$f(x)$の曲がり具合を示しています。つまり、ペナルティ項を加えることで曲線の当てはまり具合と曲線のグニャグニャ度のバランスをとった回帰曲線$f(x)$を求めたい、というアイディアです。ペナルティ項の影響の強さを決める定数$\lambda$を平滑化パラメータと呼びます。
実はペナルティ付き二乗誤差を最小化する$f(x)$は$x_i$をknotとする3次自然スプラインであることが知られています。ただし、データ数が十分多い時は$x_i$全てをknotにはせずに、データの中からいくつか選ぶことが多いと思います。したがって、以下のように3次自然スプライン基底のデザイン行列$\boldsymbol{X}$を使ってペナルティ付き二乗誤差を表現することができます。
(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})^T(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})+\lambda\boldsymbol{\beta}^T\boldsymbol{S}\boldsymbol{\beta}
ここで、行列$\boldsymbol{S}$は$(i, j)$成分$s_{ij}$が
s_{ij} = \int_{x_0}^{x_n}b_i''(x)b_j''(x)dx
であるようなペナルティ行列です。パラメータ推定値$\boldsymbol{\hat{\beta}}$は以下のよう計算することができます。
\boldsymbol{\hat{\beta}}=(\boldsymbol{X}^T\boldsymbol{X}+\lambda\boldsymbol{S})^{-1}\boldsymbol{X}^T\boldsymbol{y}
それでは実際にペナルティ付き最小二乗法で平滑化パラメータ$\lambda$の値とknotの数を変えながら回帰曲線を描いてみましょう。
平滑化パラメータ$\lambda$の値が小さいと回帰曲線はグニャグニャした形になり、大きくすると平坦な形になることがわかります。また、平滑化パラメータ$\lambda$の値を固定するとknotの数を変えても曲線の形がほとんど変化しません。したがって、ペナルティ付き最小二乗法を使用することによって曲線の形はほとんど$\lambda$で決定されることになります。そのため、柔軟な回帰曲線が描けるようにknotを数を多めにしておいて、最適な$\lambda$を選ぶことで過剰適合を防ぐ、という戦略で回帰分析を行います。
このような3次自然スプラインを用いたペナルティ付き最小二乗法はcubic regression splineとしてGAMで多く利用されているようです。GAMは普通の線形回帰を含むモデルですが、実際はスプラインを利用した非線形回帰を指していることが多いと思います。
Rのパッケージを活用しよう
実際にGAMによる回帰分析を行う場合は、自分で正規方程式を解いても良いですが、既存のパッケージを使用する方がプログラミングも簡単だし正確な結果が得られます。2今回はRのmgcvパッケージを使用してGAMを行うことにします。以下のプログラムで簡単にGAMを行って回帰曲線を得ることができます。
library("tidyverse")
library("mgcv")
# GAMの実行
gam.model <- gam(y~s(x, bs = "cr"), data = test.data)
# 予測値の計算
x <- tibble(x = seq(0, 20, by = 0.005)) #説明変数のデータセット
y <- predict(gam.model, x) #予測値の計算
gam.pred <- x %>% dplyr::mutate(y = y) #予測値と説明変数のデータセット(プロット用)
# プロット
ggplot(NULL) +
geom_point(data = test.data, aes(x = x, y = y)) +
geom_line(data = gam.pred, aes(x = x, y = y), color = "orange") +
# knotの可視化
geom_vline(xintercept = gam.model$smooth[[1]]$xp, linetype = "dashed", color = "blue")

gam関数を使ってGAMによる回帰分析を行います。「test.data」はy列に応答変数、x列に説明変数が入っているデータフレームです。モデルの式の書き方はlm関数と基本的に同じですが、説明変数をs()で囲む必要があります。s()の中の「bs = "cr"」でcubic regression splineを指定しています。
gam関数を使えばknotも平滑化パラメータもいい感じの値を自動で選んでくれます。もし自分でknotと平滑化パラメータを指定したい場合は以下のようにすればOKです。
# knots
knot_list <- list(x = seq(0, 20, length.out = 10))
# GAMの実行
gam.model <- gam(y~s(x, bs = "cr", k = 10, sp = 1), knots = knot_list, data = test.data)
knotはリストにしてgam関数の「knots」のところで指定します。また、s()の中の「k」でknotの数を指定します。リストに含まれるknotの数と「k」で指定したknotの数は一致している必要があります。平滑化パラメータはs()の中の「sp」で指定することができます。
このようにmgcv等のパッケージを使うと簡単にGAMを実装できるのでとても便利です。
平滑化パラメータの選び方
mgcvのgam関数を使用すると自動的に平滑化パラメータの値を選んでくれますが、どのように選んでいるのでしょうか。まず、選ばれた平滑化パラメータは以下のように確認することができます。
> gam.model$sp
s(x)
0.08077458
この平滑化パラメータはデフォルトでは一般化クロスバリデーション(Generalized Cross Validation:GCV)誤差を最小にするという基準で選ばれています。以下でGCV誤差とは何かについて説明します。
予測値$\boldsymbol{\hat{y}}$が実際の観測値$\boldsymbol{y}$によらない行列$\boldsymbol{H}$を用いて、
\boldsymbol{\hat{y}}=\boldsymbol{H}\boldsymbol{y}
と表現することができるとします。ペナルティ付き最小二乗法では、
\boldsymbol{\hat{y}}=\boldsymbol{X}\boldsymbol{\hat{\beta}}=\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X}+\lambda\boldsymbol{S})^{-1}\boldsymbol{X}^T\boldsymbol{y}
ですから、
\boldsymbol{H}=\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X}+\lambda\boldsymbol{S})^{-1}\boldsymbol{X}^T
となるので、条件を満たしていることがわかります。このとき、一個抜き交差検証(leave-one-out cross-validation:LOOCV)誤差は訓練データと検証データを分けずに全てのデータを使用して作ったモデルから以下のように計算することができます。
LOOCV=\frac{1}{n}\sum_{i=1}^{n}\bigl(\frac{y_i-\hat{y_i}}{1-H_{ii}}\bigl)^2
$H_{ii}$は行列$\boldsymbol{H}$の$(i, i)$成分です。GCV誤差は以下のように$H_{ii}$の部分を行列$\boldsymbol{H}$の対角成分の平均で置き換えた値です。
GCV=\frac{1}{n}\sum_{i=1}^{n}\bigl(\frac{y_i-\hat{y_i}}{1-\frac{tr\boldsymbol{H}}{n}}\bigl)^2
GCVはLOOCVに比べて計算が容易・尺度変換に対して不変といったメリットがあるようです。どちらの基準も汎化性能を考慮した上で平滑化パラメータを決めようという基準になっています。
平滑化パラメータを変えながらGCVとLOOCVの値をプロットしてみます。x軸は平滑化パラメータ、y軸はGCV(赤線)とLOOCV(青線)の値です。縦の点線でそれぞれの値が最小になる位置を示しています。点線の位置のx軸の値が最終的な平滑化パラメータの値として選択されます。GCVとLOOCVでは若干異なる平滑化パラメータが選択されることもわかります。

説明変数を増やす
ここまで1変数の場合のみを扱ってきました。説明変数が増えても基本的に同じ考え方でGAMを行うことができますが、少し変わるところもあります。例えば説明変数が$x_{1}$と$x_{2}$の2つある時は、
y_i=f(x_{i1})+g(x_{i2})+\epsilon_i, \hspace{5pt}\epsilon_i\tilde{}\hspace{2pt}N(0, \sigma^2)\hspace{20pt} (i=1, 2, \ldots, n)
のように表して$f$と$g$の2つの関数を推定することになります。そして、これまでと同じように$f$と$g$それぞれを基底関数の線形結合で表して未知パラメータを推定します。そのため変数が増えるとそれぞれの説明変数について①基底関数の選択、②(必要な場合は)knotの選択、③平滑化パラメータの選択、といった作業を行う必要があります。でも、パッケージに任せるだけで問題なければ説明変数が増えても手間はほとんど変わりません。
mtcarsデータを使ってcubic regression splineを用いたGAMを行ってみます。目的変数をmpg(燃費)、説明変数は適当にdisp(排気量), hp(馬力), wt(重量)を使うことにします。
gam.model <- gam(mpg ~ s(disp, bs = 'cr') + s(hp, bs = 'cr') + s(wt, bs = 'cr'), data = mtcars)
説明変数と目的変数の間にどのような関係があるかを知りたいので、推定したパラメータを確認します。
> gam.model$coefficients
(Intercept) s(disp).1 s(disp).2 s(disp).3 s(disp).4 s(disp).5 s(disp).6 s(disp).7 s(disp).8 s(disp).9
20.0906250 3.4033025 -1.4169032 0.1685064 -4.1810545 -2.8412124 -5.3363467 -4.5008059 -0.3994391 -4.6846908
s(hp).1 s(hp).2 s(hp).3 s(hp).4 s(hp).5 s(hp).6 s(hp).7 s(hp).8 s(hp).9
1.0216879 0.7326252 0.5458943 0.2105009 -0.2632256 -1.6608013 -1.3946367 -2.3547655 -3.2957380
s(wt).1 s(wt).2 s(wt).3 s(wt).4 s(wt).5 s(wt).6 s(wt).7 s(wt).8 s(wt).9
1.9501294 1.0466587 -0.1145877 -0.9706933 -0.9238744 -2.7207909 -2.3510963 -2.6440014 -6.0883345
少し見辛いですが、各説明変数に対するパラメータ推定値を確認することができます。デフォルトでは各説明変数に対して10個のknotが設定されるので、説明変数が3つの場合は未知パラメータの数は30個になります。ただし、3次自然スプライン基底の一つ目の基底関数$b_1(x)=1$に対応する未知パラメータについては、説明変数が複数あると一意に決めることができないので、(Intercept)という形で一つにまとめられています。したがって、上記では28個のパラメータ推定値が表示されています。
説明変数を基底関数を用いて変換しているので、パラメータ推定値を見ても何を意味しているかよくわかりません。各説明変数に対して関数(上の例では$f$とか$g$とか)を推定しているので、それをプロットすることにします。plot(gam.model)だけで済むんですが、見た目が気に入らないので、少し頑張ってggplotを使います。
library("gridExtra")
plot <- plot(gam.model, residual = TRUE)
for (i in 1:3){
g <- ggplot(NULL) +
geom_point(data = tibble(x = plot[[i]]$raw, y = plot[[i]]$p.resid), aes(x = x, y = y)) +
geom_line(data = tibble(x = plot[[i]]$x, y = plot[[i]]$fit), aes(x = x, y = y), color = "orange", size = 1) +
geom_vline(xintercept = gam.model$smooth[[i]]$xp, linetype = "dashed", color = "blue") +
xlab(gam.model$smooth[[i]]$term) + ylab(paste('s(',gam.model$smooth[[i]]$term, ')', sep = '')) +
theme(axis.text = element_text(size = 20), axis.title = element_text(size = 25))
assign(paste('g', i, sep = ''), g)
}
layout <- rbind(c(1, 2, 3))
gridExtra::grid.arrange(g1, g2, g3, layout_matrix = layout)
モデルの良し悪しはともかくとして、プロットすると説明変数が応答変数にどのような影響を与えるかが分かりやすくなりますね。プロットを見てみるとhpとwtはほぼ直線になっています。全ての説明変数を3次自然スプライン基底で変換する必要はないので、このような説明変数は普通の線形の項としてモデルに入れた方が、通常の回帰係数が得られるのでモデルの意味が分かりやすくなると思います。以下のように説明変数をs()で囲うのをやめればOKです。
gam.model <- gam(mpg ~ s(disp, bs = 'cr') + hp + wt, data = mtcars)
> summary(gam.model)
#一部省略してます
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.247349 4.000423 7.561 1.21e-07 ***
hp -0.017224 0.009028 -1.908 0.0691 .
wt -2.371666 1.196088 -1.983 0.0596 .
summaryでもパラメータ推定値を確認することができます。s()で囲んでいない変数については普通の回帰係数が表示されるので、モデルが分かりやすくなりますね。
終わりに
他にも色々なスプラインがあったり、正規分布以外の分布でもGAMを行えたりするので、その辺りもそのうちまとめたいです。
参考文献
Generalized Additive Models:an introduction with R
Part IV: Basis expansion methods
Splines and Friends: Basis Expansion and Regularization




