一般化加法モデルを用いた回帰分析②：P-spline

はじめに

こちらの記事の続きです。今回の記事ではP-splineについて勉強したことをまとめておこうと思います。

一般化加法モデル (GAM)

GAMについて簡単におさらいします。以下のような応答変数yと説明変数xのデータを用いて、非線形回帰を行うことを考えます。サインカーブにノイズを乗せて適当に作ったデータです。

R

> test.data
# A tibble: 101 x 2
       x       y
   <dbl>   <dbl>
 1   0    0.635 
 2   0.2  0.0663
 3   0.4 -0.525 

# プロット
ggplot(data = test.data, aes(x = x, y = y)) +
  geom_point()

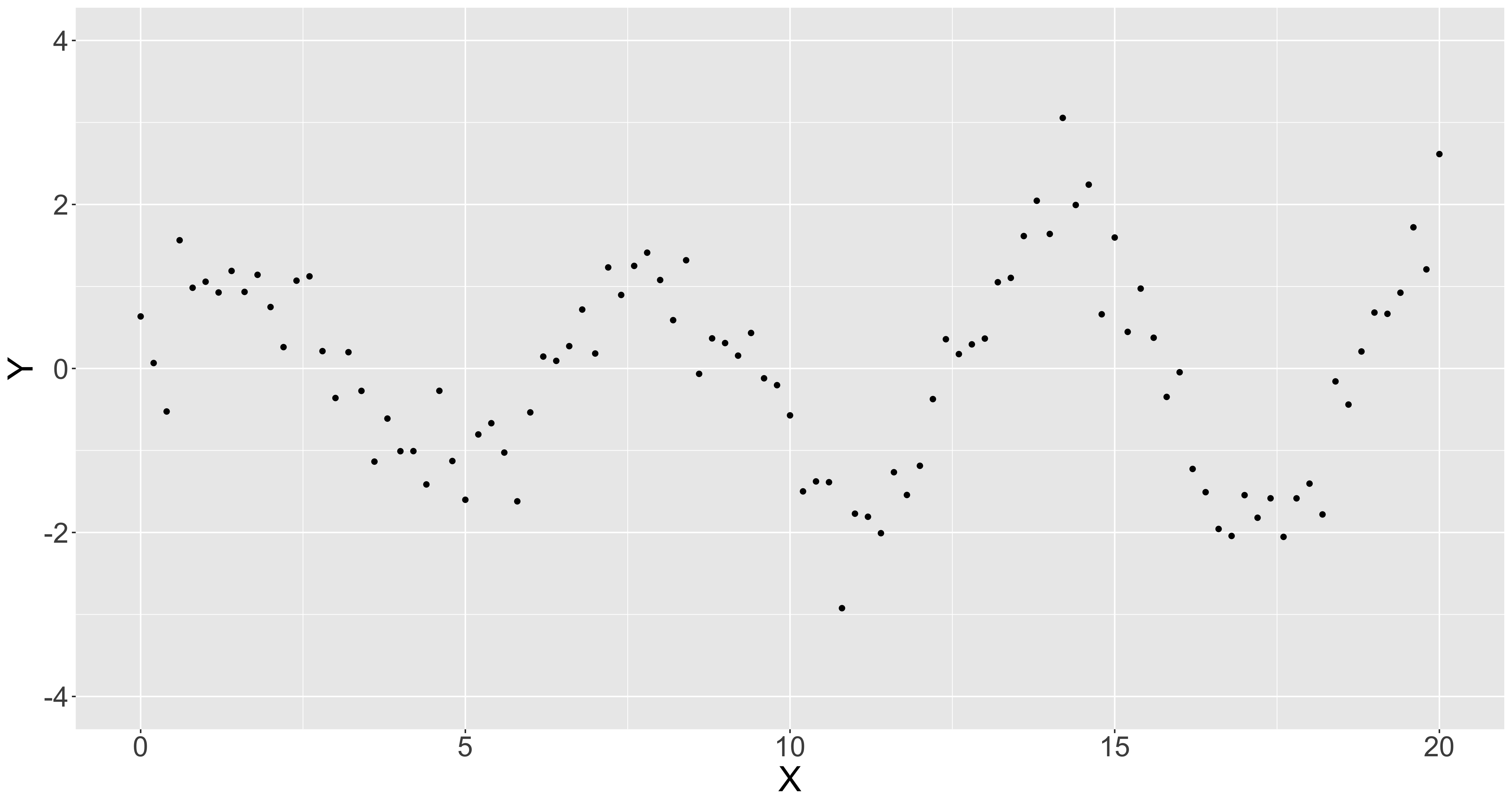
GAMでは応答変数$y$と説明変数$x$の関係を以下のように表現します。

y_i=f(x_i)+\epsilon_i, \hspace{5pt}\epsilon_i\tilde{}\hspace{2pt}N(0, \sigma^2)\hspace{20pt} (i=1, 2, \ldots, n)

そして、$f(x)$を既知の$p$個の基底関数$b_j(x)$と未知のパラメータ$\beta_j$の線形結合として

f(x)=\sum_{j=1}^{p}\beta_j b_j(x)

のように表現することで$f(x)$の推定を未知のパラメータ$\beta_j$の推定に置き換えて回帰分析を実行することが可能になるのでした。今回の記事では基底関数としてB-splineを使用して、そこにパラメータに対するペナルティを設定したP-splineを用いたGAMについて考えることにします。

B-spline

スプラインを表現する方法の一つにB-splineを用いる方法があります。未知パラメータの数を$p$とすると、m次のB-spline基底関数$B^m_j(x)$は以下のように再帰的に定義される関数です。

B^m_j(x) = \frac{x-a_j}{a_{j+m}-a_j}B^{m-1}_j(x)\hspace{2pt}+\hspace{2pt}\frac{a_{j+m+1}-x}{a_{j+m+1}-a_{j+1}}B^{m-1}_{j+1}(x)\hspace{20pt}(j = 1,\ldots,p)

B^{0}_j(x) = \left\{
\begin{array}{ll}
1 & (a_j \leq x < a_{j+1}) \\
0 & (otherwise)
\end{array}
\right.

上記の式の$a_j$はknotです。B-spline基底関数の定義からわかるように、$p+m+1$個のknotを定義する必要があります。また、knotを小さい方から$a_1 < a_2 < \cdots <a_{p+m+1}$とすると、データが$[a_{m+1}, a_{p+1}]$の範囲内に収まるようにデータの外側にもknotを配置する必要があります。このような基底関数を用いると、回帰曲線$f(x)$を以下のように表現することができます。　

f(x)=\sum_{j=1}^{p}\beta_j B^m_j(x)

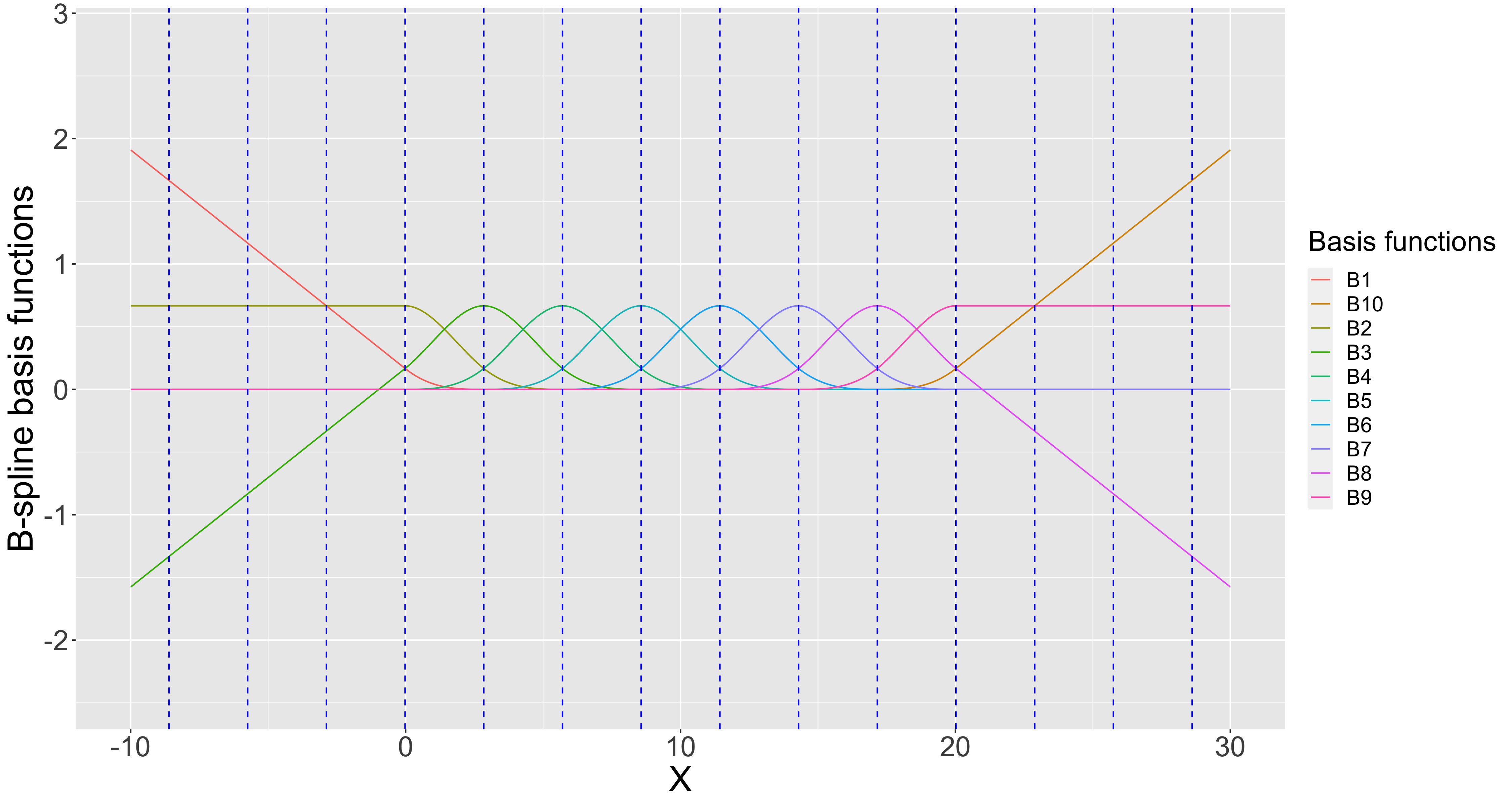
B-spline基底関数の式を見ても何が何だかよく分からないので、実際に基底関数のグラフを書いてみることにします。なお、今回の記事では$m=3$とした3次スプラインを扱い、$p=10$として未知パラメータの数は10個としています。

R

library('tidyverse')
library('splines')

# knotの定義
knots_vector <- c( -8.608571, -5.745714, -2.882857, -0.020000,  2.842857,  5.705714,  8.568571,
                   11.431429, 14.294286, 17.157143, 20.020000, 22.882857, 25.745714, 28.608571)

# 基底関数を作成するための説明変数xのベクトル（実際のデータより範囲広めに）
x <- seq(-10, 30, length.out = 1000)

# B-spline基底関数を作成（splineDesign関数）、データ整形
B_spline_basis <- splineDesign(knots = knots_vector, x = x, outer.ok = TRUE) %>% 
  cbind(x) %>% 
  as_tibble() %>% 
  pivot_longer(cols = V1:V10) %>% 
  arrange(name, x)
 
# プロット
ggplot(NULL) +
  geom_line(data = B_spline_basis, aes(x = x, y = value, color = name)) +
  geom_vline(xintercept = knots_vector, color = 'blue', linetype = 'dashed') 

上記のグラフでは14個のknot（青の縦破線）を定めて10個の3次B-spline基底関数を作っています。グラフを見るとそれぞれのB-spline基底は隣接したknot 5個分の領域でのみ非ゼロの値をとることがわかります。このように基底関数の値が局所的な領域でのみ非ゼロになることがB-spline基底の特徴の一つになっています。また、データの範囲は0~20なのでデータの外側にもknotが定義されていることもわかります。　

今回のデータでB-spline基底を用いたGAMを行うには、説明変数をB-spline基底で変換してから最小二乗法でパラメータを推定すれば良いので、簡単に実行することができます。

R

# 説明変数をB-spline基底で変換
B_spline_data <- splineDesign(knots = knots_vector, x = test.data$x) %>% 
  as_tibble() %>% 
  mutate(y = test.data$y)

# パラメータを推定
model <- lm(y ~ . -1, data = B_spline_data)

# 回帰曲線を描画
B_spline_data <- B_spline_data %>% 
  mutate(pred = predict(model, B_spline_data),
         x = test.data$x)

ggplot(data = B_spline_data) +
  geom_point(aes(x = x, y = y)) +
  geom_line(aes(x = x, y = pred), color = 'orange', size = 1)

P-spline

B-splineもknotの数を増やしていけばかなり柔軟な曲線を表現することができます。しかし、その分だけオーバーフィッティングも起こりやすくなっています。したがって、B-spline基底を用いてGAMを行う場合、何らかの方法で曲線の柔軟性を抑制することが必須になります。曲線の柔軟性を抑制するペナルティを設定したB-splineをP-splineと呼びます。

前回の記事の3次スプラインでは以下のように回帰曲線の2階微分の積分をペナルティ項として用いることで曲線のグニャグニャ度を制御していました。

\int_{x_0}^{x_n}\{f''(x)\}^2dx

一方で、P-splineでは各B-spline基底関数のパラメータに対して差分ペナルティ (difference penalty)と呼ばれるペナルティを導入することで曲線の柔軟性を制御します。差分ペナルティとは隣接する基底関数に対するパラメータの差をペナルティとして用いる方法です。Fused LASSOと似たようなイメージがわかりやすいと思います。例として以下に1階及び２階の差分ペナルティを示しています。　

1階の差分ペナルティ:\sum_{j=1}^{}(\beta_{j+1}-\beta_j)^2

2階の差分ペナルティ:\sum_{j=1}^{}\{(\beta_{j+2}-\beta_{j+1})-(\beta_{j+1}-\beta_j)\}^2=\sum_{j=1}^{}(\beta_{j+2}-2\beta_{j+1}+\beta_j)^2

B-spline基底は局所的な領域でのみ非ゼロの値をとるため、隣接するパラメータの値の差が小さいほど回帰曲線のグニャグニャ度は小さくなります。試しに回帰曲線のグニャグニャ度合いを変えてその時の差分ペナルティの値を見てみることにします。　

各グラフの左上に1階の差分ペナルティの値を示しています。確かに差分ペナルティの値が小さいほど回帰曲線のグニャグニャ度が小さくなっていることが確認できます。したがって、P-splineを用いたGAMでは以下のペナルティ付き二乗誤差を最小化するようなパラメータを推定することで回帰曲線の当てはまりとグニャグニャ度のバランスをとった、汎化性能の高いモデルを作ります。

\sum_{i=1}^{n}\{y_i-\sum_{j=1}^{p}\beta_j B^2_j(x_i)\}^2+\lambda\sum_{j=1}^{p-1}(\beta_{j+1}-\beta_j)^2

$\lambda$は平滑化パラメータです。上記の式では例として1階の差分ペナルティを用いていますが、2階やそれ以上の差分ペナルティを用いることも可能です。B-spline基底と差分ペナルティを用いることでかなり簡単な形で回帰曲線のグニャグニャ度に対するペナルティを設定することができました。　

P-splineを用いた1説明変数のGAMについては簡単に実装することができます。上記の目的関数を行列を用いて表現すると、

||\boldsymbol{y}-\boldsymbol{X\beta}||^2+\lambda\boldsymbol{\beta}^T\boldsymbol{S\beta}=\begin{Vmatrix}
\left[
\begin{array}{ll}
\boldsymbol{y}  \\
\boldsymbol{0}
\end{array}
\right]-
\left[
\begin{array}{ll}
\boldsymbol{\hspace{5pt}X}  \\
\boldsymbol{\sqrt{\lambda}D}
\end{array}
\right]\boldsymbol{\beta}
\end{Vmatrix}^2

のようになります。$\boldsymbol{y}$は目的変数ベクトル、$\boldsymbol{X}$はB-spline基底を用いたデザイン行列、$\boldsymbol{\beta}$は未知パラメータベクトル、$\boldsymbol{S}$はペナルティ行列、$\boldsymbol{D}$は$\boldsymbol{D}^T\boldsymbol{D}=\boldsymbol{S}$を満たす行列です。行列$\boldsymbol{S}$、$\boldsymbol{D}$は何階の差分ペナルティを用いるかによって変化します。$\boldsymbol{D}$の具体的な形は以下のプログラムを実行して確認できます。右辺はペナルティ無しの二乗誤差になっているので、右辺のように変換した行列に対して通常の最小二乗法でパラメータの推定を行います。また、既存の関数を使わずにB-spline基底を用いた変換を行なってみます。

R

# knotを決める
knots_vector <- c( -8.608571, -5.745714, -2.882857, -0.020000,  2.842857,  5.705714,  8.568571,
                   11.431429, 14.294286, 17.157143, 20.020000, 22.882857, 25.745714, 28.608571)

# 3次のB-spline基底を用いて説明変数を変換
bspline <- function(x, i, k = knots_vector, m = 3){
  if (m == 0){ 
    res <- as.numeric(x < k[i+1] & x >= k[i])
  } else { 
    z0 <- (x - k[i])/(k[i+m] - k[i])
    z1 <- (k[i+m+1] - x)/(k[i+m+1] - k[i+1])
    res <- z0*bspline(x, i, k, m-1) + z1*bspline(x, i+1, k, m-1) 
  }
  res 
}

for (j in 1:(length(knots_vector)-4)){
  test.data <- test.data %>%
    mutate(temp = mapply(bspline, x = x, i = j)) 
  colnames(test.data)[j+2] <- paste('B', j, sep = '')
}

# デザイン行列X, 目的変数ベクトルyを作成
X <- as.matrix(test.data[3:12])
y <- as.matrix(test.data$y)

# 行列Dを作成（2階の差分ペナルティを使用、differencesで指定）
D <- diff(diag(length(knots_vector)-4), differences = 2)

# 平滑化パラメータ
lambda <- 0

ここまでで必要な行列を準備することができたので、これらを用いて未知パラメータの推定を行います。平滑化パラメータの値は適当に変えてください。今回はデザイン行列のQR分解を行い、後退代入によって連立方程式を解くことで未知パラメータの値を求めます。

R

# 目的関数の右辺の形に行列を変形
X_aug <- rbind(X, sqrt(lambda)*D)
y_aug <- rbind(y, matrix(0, ncol = 1, nrow = nrow(D)))

# QR分解+パラメータ推定
QR <- qr(X_aug)
parameters <- backsolve(qr.R(QR), qr.qty(QR, y_aug))

# 予測値計算
fitted.values <- X %*% parameters

パラメータ推定〜予測値計算の流れはこのような感じになります。平滑化パラメータをいろいろ変えて回帰曲線を描いてみましょう。各グラフの左上に平滑化パラメータの値を示しています。平滑化パラメータを変えることで曲線の形が変化する様子が確認できます。

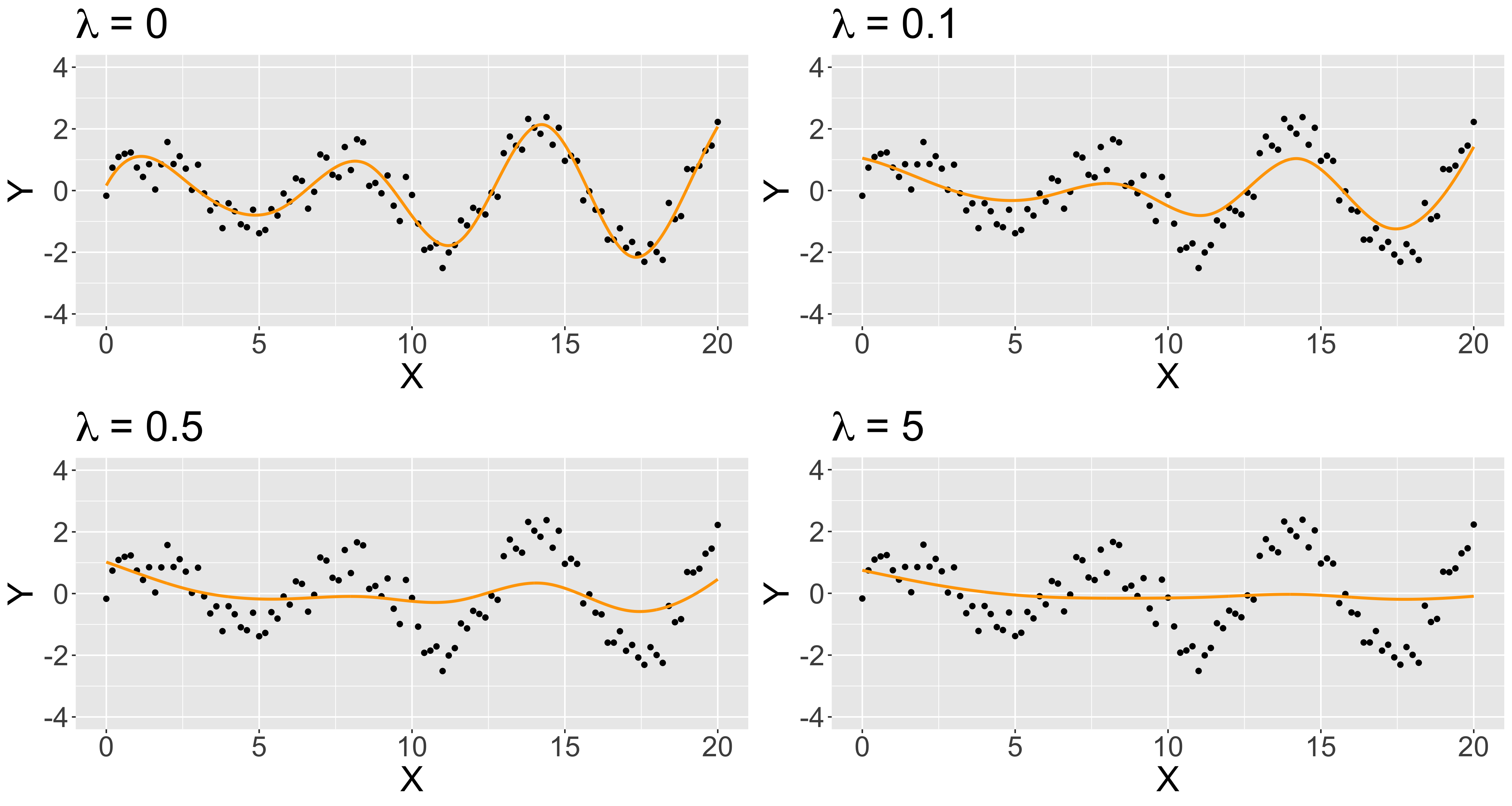
自然スプラインにする

次に回帰曲線をデータの範囲外まで伸ばしてみることにします。

上のグラフを見るとデータ範囲外でも回帰曲線が振動している、knotの外側では予測値が常に0になる、ということがわかります。つまり、B-spline基底そのままでは自然スプラインになっていません。そこで、B-splineを自然スプラインにすることを考えます。　

B-splineを自然スプラインにするには、未知パラメータの推定は先ほどと同様に行い、新規データの予測を行う際に外挿領域のデータのB-spline基底関数変換にこれまでとは異なる処理を入れればOKです。Rのコードを以下に示します。　

R

# 外挿領域を含んだデータを作成
test.data.extra <- tibble(x = seq(-15, 35, length.out = 1000))
x <- test.data.extra$x
n <- length(x)

# 特定の位置のknotの値を抽出
ll <- knots_vector[4]
ul <- knots_vector[length(knots_vector) - 3]

# 抽出したknotでのB-spline基底の値、その微分値を取得
D <- splineDesign(knots_vector, c(ll, ll, ul, ul), 4, c(0, 1, 0, 1))

# B-spline基底での変換結果を格納する行列を初期化
X <- matrix(0, n, ncol(D)) 

# 内挿範囲のデータは普通のB-spline基底で変換
ind <- x <= ul & x >= ll 
if (sum(ind) > 0){
  X[ind, ] <- splineDesign(knots_vector, x[ind])
}

# 外挿範囲（小さい側）のデータを変換
ind <- x < ll
if (sum(ind) > 0){
  X[ind, ] <- cbind(1, x[ind] - ll) %*% D[1:2, ]
}

# 外挿範囲（大きい側）のデータを変換
ind <- x > ul
if (sum(ind) > 0){
  X[ind, ] <- cbind(1, x[ind] - ul) %*% D[3:4, ]
}

上記の流れで作成した変数Xに説明変数を自然スプライン化したB-spline基底で変換した結果が格納されています。ごちゃごちゃ変換しましたが、実際に基底関数の形を見てみた方がわかりやすいのでプロットしてみます。

通常のB-spline基底とは異なり、データの範囲の末端のknot位置で非ゼロの値を持つ基底関数のグラフがその部分から真っ直ぐに伸びていることがわかります。このように変換した行列（変数X）にパラメータ推定値のベクトルを掛けることで外挿範囲を含んで予測値を算出・回帰曲線を描いてみます。

上のグラフに回帰曲線を示しています。オレンジがB-splineを自然スプラインになるように変換した曲線、黒が普通のB-splineを用いた曲線です。オレンジの曲線はデータの範囲外では直線になっており、自然スプラインになっていることがわかると思います。自然スプラインが良いのか、普通のB-splineが良いのかは状況によって変わってくると思うので必要に応じて使い分けができると良いのかなと思います。そもそもGAMに限らず外挿は難しいと思うので注意が必要ですね。

多変数に拡張する

制約条件を用いたモデルの書き換え

ここまでは説明変数が1つの場合について考えてきましたが、ここではP-splineを用いたGAMを多変数に拡張することを考えます。例として、以下のように説明変数が二つの場合を考えます。

y_i=f(x_{1i})+g(x_{2i})+\epsilon_i, \hspace{5pt}\epsilon_i\tilde{}\hspace{2pt}N(0, \sigma^2)\hspace{20pt} (i=1, 2, \ldots, n)

そして、$f(x_1), g(x_2)$を3次のB-spline基底$B_{1j}(x_{1}), B_{2j}(x_2)$と未知のパラメータ$\beta$の線形結合として

f(x_1)=\sum_{j=1}^{}\beta_{1j} B_{1j}(x_1)

g(x_2)=\sum_{j=1}^{}\beta_{2j} B_{2j}(x_2)

のように表現できるとします。しかし、2つの説明変数をB-spline基底で変換しても未知パラメータを一意に推定することができません。なぜなら、$f(x_1)$をある一定量上側にシフトさせた時、$g(x_2)$をその分下側にシフトさせればモデルとしては同一になるからです。そこで、$\sum f(x_{1i})=0$、$\sum g(x_{2i})=0$となるような制約条件を入れることで$f(x_1)、g(x_2)$の位置が0を中心に固定されるようにします。

上記の内容は一般的には以下のような制約条件付き最小二乗法として表現することができます。

minimize\hspace{5pt}||\boldsymbol{y}-\boldsymbol{X\beta}||^2\hspace{5pt}subject\hspace{2pt}to\hspace{5pt}\boldsymbol{C\beta}=\boldsymbol{0}

ここで$\boldsymbol{y}$はn次元目的変数ベクトル、$\boldsymbol{X}$はn×pデザイン行列、$\boldsymbol{\beta}$はp次元未知パラメータベクトル、$\boldsymbol{C}$は制約条件を表すm×p行列とします。これはデザイン行列と未知パラメータを上手く書き換えることで制約条件無しの最小二乗法に帰着させることができます。まず、$\boldsymbol{C}^T$に対してQR分解を行い、

\boldsymbol{C}^T = \boldsymbol{QR}= [\boldsymbol{Q_1}\hspace{2pt}\boldsymbol{Q_2}]\left[
\begin{array}{ll}
\boldsymbol{R_1}  \\
\hspace{2pt}\boldsymbol{0}
\end{array}
\right]

のように得られたp次直交行列$\boldsymbol{Q}$をp×m行列$\boldsymbol{Q_1}$とp×(p-m)行列$\boldsymbol{Q_2}$に分割します。また、$\boldsymbol{R}$はm×m上三角行列$\boldsymbol{R_1}$と残りの部分のゼロ行列に分割します。ここで、行列$\boldsymbol{Q_2}$を用いて

\boldsymbol{\beta} = \boldsymbol{Q_2\beta_{new}}

となるような新しい未知パラメータベクトル$\boldsymbol{\beta_{new}}$を作成します。ここで制約条件を考えると、

\boldsymbol{C\beta}=(\boldsymbol{QR})^T\boldsymbol{Q_2\beta_{new}}=[\boldsymbol{R_1}^T\hspace{2pt}\boldsymbol{0}]\left[
\begin{array}{ll}
\boldsymbol{Q_1}^T  \\
\boldsymbol{Q_2}^T
\end{array}
\right]
\boldsymbol{Q_2\beta_{new}}=[\boldsymbol{R_1}^T\hspace{2pt}\boldsymbol{0}]\left[
\begin{array}{ll}
\boldsymbol{0}  \\
\boldsymbol{I}
\end{array}
\right]\boldsymbol{\beta_{new}}=\boldsymbol{0}

となり、$\boldsymbol{\beta_{new}}$の値によらず常に制約条件が満たされることになります。したがって、二乗誤差を

||\boldsymbol{y}-\boldsymbol{X\beta}||^2=||\boldsymbol{y}-\boldsymbol{XQ_2\beta_{new}}||^2

のように書き換え、新しいデザイン行列を$\boldsymbol{XQ_2}$として新しい未知パラメータ$\boldsymbol{\beta_{new}}$を最小二乗推定することが、最初の制約条件付き最小二乗法を解く事と等しくなります。最後に$\boldsymbol{\beta_{new}}$の推定値$\boldsymbol{\hat{\beta}_{new}}$を用いて、　

\boldsymbol{\hat{\beta}}=\boldsymbol{Q_2\hat{\beta}_{new}}

のように元のパラメータの推定値を求めます。

今回のP-splineにおける制約条件は、まず$\sum f(x_{1i})=0$に着目して、$\boldsymbol{B_f}$を説明変数$x_1$をB-spline基底を用いて変換したデザイン行列、$\boldsymbol{\beta_f}$を$\boldsymbol{B_f}$に対応する未知パラメータのベクトル、$\boldsymbol{1}$を全ての成分が1の列ベクトルとすると、　

\boldsymbol{1}^T\boldsymbol{B_f\beta_f}=\boldsymbol{0}

と表現することができます。そこで、$(\boldsymbol{1}^T\boldsymbol{B_f})^T$をQR分解して得た直交行列の分割$\boldsymbol{Z_f}$（$\boldsymbol{Q_2}$に対応）を用いて、新しいデザイン行列$\boldsymbol{B_fZ_f}$と$\boldsymbol{\beta_f}=\boldsymbol{Z_f\beta_{fnew}}$となるような新しい未知パラメータ$\boldsymbol{\beta_{fnew}}$を考えます。また、$g(x_2)$に関する制約条件についても同様に考え、新しいデザイン行列を$\boldsymbol{B_gZ_g}$、新しい未知パラメータを$\boldsymbol{\beta_{gnew}}$とします。そして、モデル全体のデザイン行列$\boldsymbol{B}$と未知パラメータベクトル$\boldsymbol{\beta}$を

\boldsymbol{B} = [\boldsymbol{1}\hspace{5pt}\boldsymbol{B_fZ_f}\hspace{5pt}\boldsymbol{B_gZ_g}]

\boldsymbol{\beta}^T = [\beta_0^T\hspace{5pt}\boldsymbol{\beta_{fnew}}^T\hspace{5pt}\boldsymbol{\beta_{gnew}}^T]

として、未知パラメータを最小二乗法によって推定します。なお、制約条件により各曲線が平均0の位置に固定されてしまうため、モデルに切片$\beta_0$を追加することでデータへのモデルの当てはめを可能にしています。通常、切片に対応する未知パラメータの値は目的変数の平均値になります。また、$\boldsymbol{Z_f}$を用いれば$\boldsymbol{\hat{\beta}_{fnew}}$を元のB-spline基底に対するパラメータに戻すことも可能ですが、そもそもB-spline基底に対する個々のパラメータに意味を与えることが難しく、回帰曲線そのものに興味がある場合が多いため、パラメータを戻す必要はあまり無いと思います。

以下のRのコードで実際に新しいデザイン行列の作成を行い、プロットして形を確認してみます。例として、mtcarsデータセットを使用して目的変数をmpg（燃費）、説明変数をwt（重量）、disp（排気量）としてP-splineを用いたGAMを行います。途中までは自然スプラインを作った時と同じです。

R

# mtcarsデータ
> head(mtcars, n = 3)
               mpg cyl disp  hp drat    wt  qsec vs am gear carb
Mazda RX4     21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag 21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
Datsun 710    22.8   4  108  93 3.85 2.320 18.61  1  1    4    1

# Data
wt <- mtcars$wt
disp <- mtcars$disp
mpg <- as.matrix(mtcars$mpg)
n <- nrow(mtcars)

# knot vector
knot_wt <- c(-0.1704061, 0.3894256, 0.9492573, 1.5090890, 2.0689207, 2.6287524, 3.1885841, 
             3.7484159, 4.3082476, 4.8680793, 5.4279110, 5.9877427, 6.5475744, 7.1074061)
knot_disp <- c(-101.45881, -44.07284, 13.31313, 70.69910, 128.08507, 185.47104, 242.85701,
               300.24299, 357.62896, 415.01493, 472.40090, 529.78687, 587.17284, 644.55881)

# 特定の位置のknotの値を抽出
ll_wt <- knot_wt[4]
ul_wt <- knot_wt[length(knot_wt) - 3]

ll_disp <- knot_disp[4]
ul_disp <- knot_disp[length(knot_disp) - 3]

# 抽出したknotでのB-spline基底の値、その微分値を取得
D_wt <- splineDesign(knot_wt, c(ll_wt, ll_wt, ul_wt, ul_wt), 4, c(0, 1, 0, 1))
D_disp <- splineDesign(knot_disp, c(ll_disp, ll_disp, ul_disp, ul_disp), 4, c(0, 1, 0, 1))

# B-spline基底での変換結果を格納する行列を初期化
B_wt <- matrix(0, n, ncol(D_wt))
B_disp <- matrix(0, n, ncol(D_disp))

# 内挿範囲のデータは普通のB-spline基底で変換
ind <- wt <= ul_wt & wt >= ll_wt 
if (sum(ind) > 0){
  B_wt[ind, ] <- splineDesign(knot_wt, wt[ind])
}

ind <- disp <= ul_disp & disp >= ll_disp
if (sum(ind) > 0){
  B_disp[ind, ] <- splineDesign(knot_disp, disp[ind])
}

# 外挿範囲（小さい側）のデータを変換
ind <- wt < ll_wt
if (sum(ind) > 0){
  B_wt[ind, ] <- cbind(1, wt[ind] - ll_wt) %*% D_wt[1:2, ]
}

ind <- disp < ll_disp
if (sum(ind) > 0){
  B_disp[ind, ] <- cbind(1, disp[ind] - ll_disp) %*% D_disp[1:2, ]
}

# 外挿範囲（大きい側）のデータを変換
ind <- wt > ul_wt
if (sum(ind) > 0){
  B_wt[ind, ] <- cbind(1, wt[ind] - ul_wt) %*% D_wt[3:4, ]
}

ind <- disp > ul_disp
if (sum(ind) > 0){
  B_disp[ind, ] <- cbind(1, disp[ind] - ul_disp) %*% D_disp[3:4, ]
}

# 制約条件の行列をQR分解して行列Zを作成
# パラメータ推定時のみ実行、予測時はこのブロックは実行しない
QR_wt <- qr(t(matrix(1, nrow = 1, ncol = n) %*% B_wt))
Z_wt <- qr.Q(QR_wt, complete = TRUE)[, 2:ncol(B_wt)]

QR_disp <- qr(t(matrix(1, nrow = 1, ncol = n) %*% B_disp))
Z_disp <- qr.Q(QR_disp, complete = TRUE)[, 2:ncol(B_disp)]

# 新しいデザイン行列Bを作成
B_wt <- B_wt %*% Z_wt
B_disp <- B_disp %*% Z_disp
B <- cbind(1, B_wt, B_disp)

このように作成した行列$\boldsymbol{B}$をデザイン行列として未知パラメータの推定を行います。実際に制約条件により変換したB-spline基底関数の形状をプロットして確認してみます。切片はwtのグラフのみに表示しています。

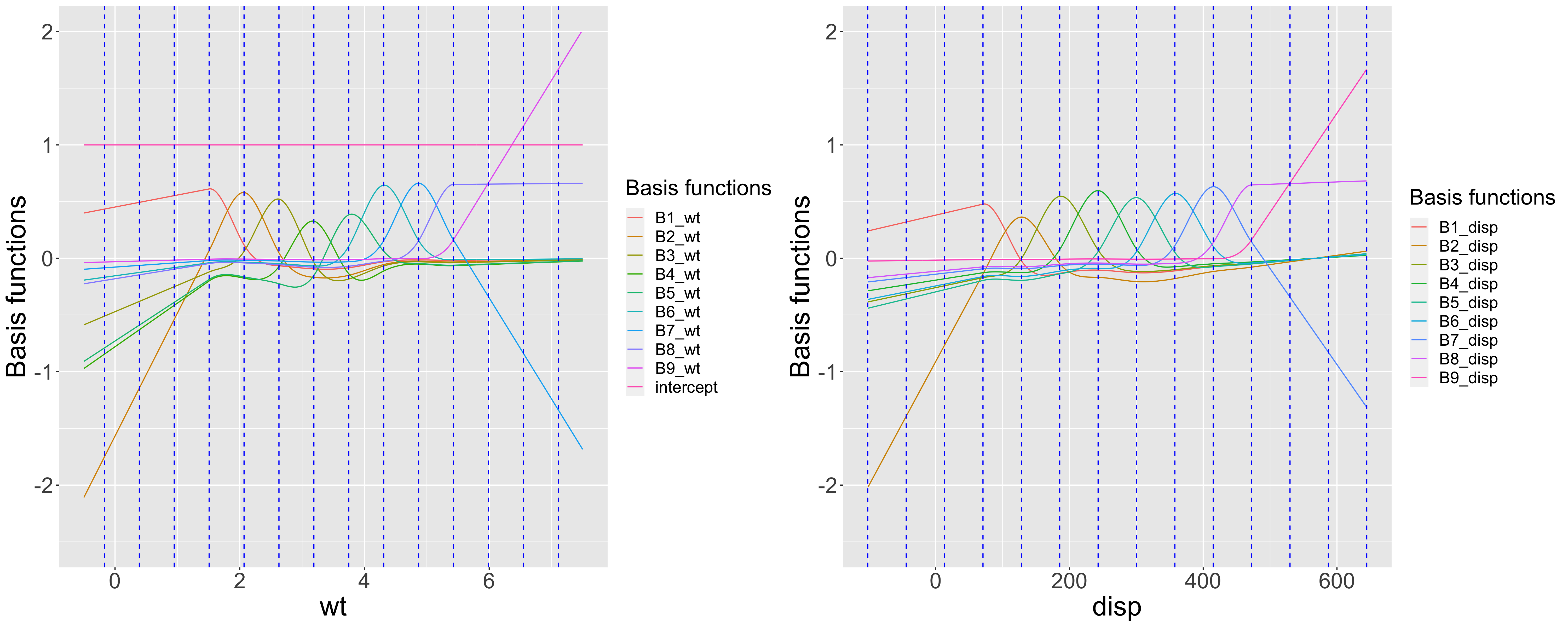
少しB-splineの面影は残っている気もしますが結構形が変わりました。また、切片を除くと各説明変数に対する基底関数の数が10個から9個になっており、制約条件によりパラメータ数が減少していることがわかります。

ペナルティの設定

未知パラメータの推定を行う前にパラメータに対してどのようにペナルティをかけるかについて考えます。B-spline基底を制約条件を用いて書き換えた新しいデザイン行列・未知パラメータを作っているため、差分ペナルティをそのまま使用しても回帰曲線のグニャグニャ度合いに対して上手くペナルティをかけることができません。しかし、実は差分ペナルティのペナルティ行列$\boldsymbol{S}$についても基底関数の書き換えに使用した行列$\boldsymbol{Z}$を用いて適切な形に変換することが可能です。

まずは$f(x_1)$について考えます。$\boldsymbol{B_f}$に対応する未知パラメータ$\boldsymbol{\beta_{f}}$の差分ペナルティを用いて作成したペナルティ行列を$\boldsymbol{S_f}$とします。この時、制約条件を用いて新規に作成したパラメータ$\boldsymbol{\beta_{fnew}}$に対するペナルティ行列$\boldsymbol{S_{fnew}}$は

\boldsymbol{S_{fnew}}=\boldsymbol{Z_f}^T\boldsymbol{S_f}\boldsymbol{Z_f}

のように作ることができます。同様に$g(x_2)$に関しても新規のパラメータ$\boldsymbol{\beta_{gnew}}$に対するペナルティ行列を$\boldsymbol{S_{gnew}}$とします。$f(x_1)$、$g(x_2)$に対する平滑化パラメータをそれぞれ$\lambda_f、\lambda_g$とすると、制約条件で書き換えた時のモデル全体のペナルティ行列$\boldsymbol{S}$は

\boldsymbol{S}=\begin{pmatrix}
0  & \cdots & 0 \\
\vdots & \lambda_f\boldsymbol{S_{fnew}} & \boldsymbol{0} \\
0 & \boldsymbol{0} & \lambda_g\boldsymbol{S_{gnew}}
\end{pmatrix}

となります。$\boldsymbol{S}$の1行目と1列目が全て0になっているのは回帰曲線のグニャグニャ度合いに関係しない切片にはペナルティをかけないことを意味しています。したがって、制約条件により書き換えたペナルティ付きのモデルは$\boldsymbol{D}^T\boldsymbol{D}=\boldsymbol{S}$となるような行列$\boldsymbol{D}$を用いて、以下のような二乗誤差を最小化する問題として定式化することができます。

||\boldsymbol{y}-\boldsymbol{B\beta}||^2+\boldsymbol{\beta}^T\boldsymbol{S\beta}=\begin{Vmatrix}
\left[
\begin{array}{ll}
\boldsymbol{y}  \\
\boldsymbol{0}
\end{array}
\right]-
\left[
\begin{array}{ll}
\boldsymbol{B}  \\
\boldsymbol{D}
\end{array}
\right]\boldsymbol{\beta}
\end{Vmatrix}^2

パラメータを推定する

P-splineを用いた多変量GAMの準備ができたので、上記の内容にしたがってペナルティの設定と未知パラメータの推定を行います。

R

# 平滑化パラメータ
lambda_wt <- 10
lambda_disp <- 0.1

# ペナルティ行列Sの作成
k_wt <- length(knot_wt) - 4
St <- crossprod(diff(diag(k_wt), differences = 2))
S_wt <- (t(Z_wt) %*% St %*% Z_wt)/norm(St)

k_disp <- length(knot_disp) - 4
St <- crossprod(diff(diag(k_disp), differences = 2))
S_disp <- (t(Z_disp) %*% St %*% Z_disp)/norm(St)

S <- matrix(0, ncol = k_wt+k_disp-1, nrow = k_wt+k_disp-1)
S[2:k_wt, 2:k_wt] <- lambda_wt*S_wt
S[(k_wt+1):(k_wt+k_disp-1), (k_wt+1):(k_wt+k_disp-1)] <- lambda_disp*S_disp

# 行列Dの作成
SVD <- svd(S)
D <- SVD$u %*% diag(sqrt(SVD$d)) %*% t(SVD$v) 

# パラメータ推定
B_aug <- rbind(B, D)
y_aug <- rbind(mpg, matrix(0, ncol = 1, nrow = nrow(D)))

QR <- qr(B_aug)
parameters <- backsolve(qr.R(QR), qr.qty(QR, y_aug))

> as.numeric(parameters)
 [1]  20.0906250   3.2495015   0.5237621  -1.1513342  -3.0862837
 [6]  -4.7219155  -3.7249887  -5.1613025  -7.6423625  -8.9762430
[11]  -3.7037993 -15.6287566 -10.7700353  -5.8997891 -15.1780538
[16] -14.3391167  -0.7758103  -7.3760281 -14.7432058

未知パラメータの推定値を得ることができました。切片に対応するパラメータの推定値が目的変数の平均値になっていることが確認できます。なお、使用した平滑化パラメータの値は適当に決めています。また、各曲線のペナルティ行列は定数倍しても問題ないので、差分ペナルティ行列のノルムで割算するという操作を行っています。

モデルの当てはまりの確認

パラメータの推定値が得られたので、モデルの当てはまりを確認します。まずは実測値と予測値を比較し、自由度調整済み決定係数を計算します。パラメータ推定時にペナルティを適用しているため、モデルの自由度はパラメータ数よりもペナルティの分だけ減少しています。そこで、モデルの有効自由度 (effective degrees of freedom: EDF)を用いて自由度調整済み決定係数を算出します。EDFはモデルのハット行列$\boldsymbol{H}$のトレースに等しいので$\boldsymbol{H}$を

\boldsymbol{H} = \boldsymbol{B}(\boldsymbol{B}^T\boldsymbol{B}+\boldsymbol{S})^{-1}\boldsymbol{B}^T

とすると、EDFは$tr(\boldsymbol{H})$となります。以下のプログラムでは先ほど用いたペナルティを用いて拡張したデザイン行列

\left[
\begin{array}{ll}
\boldsymbol{B}  \\
\boldsymbol{D}
\end{array}
\right]

のQR分解を用いて$tr(\boldsymbol{H})$を求めています。

R

# 予測値算出
pred_data <- tibble(actual = mpg[,1], predicted = (B %*% parameters)[,1]) %>% 
  # 残差計算
  mutate(residuals = actual - predicted) %>% 
  # wt, dispのみでそれぞれ予測値計算
  mutate(partial_pred_wt = (B[, 2:k_wt] %*% parameters[2:k_wt, , drop = FALSE])[,1],
         partial_pred_disp = (B[, (k_wt+1):(k_wt+k_disp-1)] %*% parameters[(k_wt+1):(k_wt+k_disp-1), , drop = FALSE])[,1]) %>% 
  # Partial residuals算出
  mutate(partial_residuals_wt = partial_pred_wt + residuals,
         partial_residuals_disp = partial_pred_disp + residuals)

# EDF
edf <- sum(diag((qr.Q(QR) %*% t(qr.Q(QR)))[1:n, 1:n]))

# 自由度調整済み決定係数
> 1 - (sum(pred_data$residuals**2)/(n-edf)) / 
+   (sum((pred_data$actual-mean(pred_data$actual))**2)/(n-1))
[1] 0.8955334

自由度調整済み決定係数はおよそ0.9となりました。また、各説明変数に対する回帰曲線をプロットすると以下のようになります。回帰曲線にPartial residualsを重ねてプロットしています。

モデルに制約条件を入れて切片$\beta_0$を追加しているため、モデルは以下のように表現することができます。

y_i=\beta_0+f(x_{1i})+g(x_{2i})+\epsilon_i, \hspace{5pt}\epsilon_i\tilde{}\hspace{2pt}N(0, \sigma^2)\hspace{20pt} (i=1, 2, \ldots, n)

$\beta_0$の推定値は目的変数の平均値なので、上記の回帰曲線は、説明変数がある値の時に目的変数を平均値からどれくらい変動させる効果があるかを意味しています。モデルに制約条件を入れたことによって結果の解釈もしやすくなっています。なお、回帰曲線のグニャグニャ度は平滑化パラメータによって変動するので、何らかの指標を用いてクロスバリデーション等で適切な値を設定する必要があります。

Rでmgcvを用いる

ここまでの内容はRでは以下のようにmgcvパッケージを使用することで1行で実行することができます。

R

library("mgcv")
gam.model <- gam(mpg ~ s(wt, bs = 'ps', sp = 10) + s(disp, bs = 'ps', sp = 0.1), data = mtcars)

# パラメータ推定値を表示
> gam.model$coefficients
(Intercept)     s(wt).1     s(wt).2     s(wt).3     s(wt).4     s(wt).5     s(wt).6 
 20.0906250   3.2495014   0.5237620  -1.1513342  -3.0862836  -4.7219155  -3.7249887 
    s(wt).7     s(wt).8     s(wt).9   s(disp).1   s(disp).2   s(disp).3   s(disp).4 
 -5.1613025  -7.6423624  -8.9762428  -3.7037997 -15.6287572 -10.7700352  -5.8997891 
  s(disp).5   s(disp).6   s(disp).7   s(disp).8   s(disp).9 
-15.1780538 -14.3391171  -0.7758106  -7.3760282 -14.7432062 

ここでは「bs = 'ps'」でP-splineを指定、「sp」で先ほどと同じ平滑化パラメータを設定しています。mgcvで推定したパラメータと先ほど手動で推定したパラメータ推定値が（計算上の誤差はありますが）一致していることがわかります。また、「sp」で平滑化パラメータを指定しなければ適切な値を一般化クロスバリデーションを用いて選択してくれます。色々な統計値も出力してくれるので実際にGAMを行うときはmgcvを用いるのが良いでしょう。なお、mgcvで作成したモデルで外挿範囲のデータを予測すると自然スプライン化されていることがわかります。

終わりに

P-splineを用いたmgcvの結果を再現する過程でGAMについての理解が少しずつ深まってきた気がします。

参考文献

1. Generalized Additive Models:an introduction with R
2. http://cse.naro.affrc.go.jp/takezawa/r-tips/r/20.html
3. Paul H. C. Eilers. Brian D. Marx. "Flexible smoothing with B-splines and penalties." Statist. Sci. 11 (2) 89 - 121 (1996). https://doi.org/10.1214/ss/1038425655
4. Wood, S.N. "P-splines with derivative based penalties and tensor product smoothing of unevenly distributed data." Stat Comput 27, 985–989 (2017). https://doi.org/10.1007/s11222-016-9666-x
5. Brian D. Marx, Paul H.C. Eilers. "Direct generalized additive modeling with penalized likelihood." Computational Statistics & Data Analysis, Volume 28, Issue 2, 193-209(1998). https://doi.org/10.1016/S0167-9473(98)00033-4.
6. Paul H.C. Eilers, Brian D. Marx, Maria Durbán. "Twenty years of P-splines”. SORT-Statistics and Operations Research Transactions, Vol. 39, Num. 2, 49-86 (2015)
7. Generalized Additive Models with P-splines