CNNによる画像分類：背景の影響を低減させる正則化

はじめに

CNNを用いた画像分類モデルを構築するときに、認識したい物体をちゃんと認識したモデルを作るのは結構難しかったりします。特に学習に用いるデータが少なくて偏りがあると以下の例のように画像の背景に基づいた分類モデルになってしまうこともあり得ます。

画像引用：https://arxiv.org/abs/1602.04938

この記事では画像の背景の影響を少しでも減らして認識したい物体を認識したモデルを作るための手法として、Orthogonal Sphere Regularizationという正則化があったので試してみます。

今回の記事で参考にした論文はこちら↓

使用したコードは以下のGitHubリポジトリに置いてあります。PyTorchでCNNを構築し、学習はGoogle ColaboratoryのGPUを用いて行なっています。

Orthogonal Sphere Regularization

画像$X$を入力すると$M$次元のベクトルを出力するCNNを考えます。ここでのCNNからの出力は、例えば全結合層の前のGlobal Average Poolingからの出力などのことで、分類に用いる最終的な出力ではありません。ミニバッチサイズを$d$として、$d$枚の画像をCNNに入力して得られる$d$個の$M$次元ベクトルを重ねて作る$d\times M$行列を$\boldsymbol{Z}$とします。Orthogonal Sphere (OS) Regularizationでは、この行列$\boldsymbol{Z}$を用いて以下のような正則化項を計算します。

L_{OS} = ||\hspace{2pt}\boldsymbol{Z}^T\boldsymbol{Z}-\boldsymbol{I}\hspace{2pt}||_{F}^2

ここで、$\boldsymbol{I}$は単位行列、$||\cdot||_{F}$はフロベニウスノルムです。そして通常のクロスエントロピー誤差$L_{CE}$に$L_{OS}$を加えた

L = L_{CE} + \alpha L_{OS}

をモデル全体の損失関数としてCNNの学習を行います。$\alpha$は正則化の強さを決めるハイパーパラメータです。$L_{OS}$の値はCNNから出力される特徴量ベクトル同士が直交していれば$0$になり、そうでなければ0以上の値を取ります。この正則化項はなるべく互いに相関のない特徴量を抽出するCNNを得やすくなるようにする働きをしています。

このような正則化を加えて学習を行うことで、画像背景の影響を抑えつつ、認識したい対象物により注目したモデルを学習しやすくなるようです。実際に上記の損失関数を用いてCNNの学習を行なって、Grad-CAMによる可視化を行なってみることにします。

実験してみる

使用するモデル

今回の実験ではCNNのアーキテクチャとしてResNet18を使うことにします。$L_{OS}$は全結合層の前のGlobal Average Poolingからの出力を用いて計算します。ResNet18ではGlobal Average Poolingの出力は512次元のベクトルです。ImageNetで学習済みのモデルをパラメータの初期値として学習を行います。

使用するデータ

学習用のデータには「Tiny ImageNet」データを使用します。これはImageNetの小さい版で、200分類の画像があり、各分類に対して500枚の訓練用画像、100枚の検証用/テスト用画像が含まれています。あまりたくさんのデータで学習するのは大変なのでこの小さめのデータセットで実験を行います。

モデルの実装

今回の実験では損失関数の計算にResNet18からの最終的な出力だけでなく、途中のGlobal Average Pooling層からの出力も必要になるので、少しモデルを書き換える必要があります。また、「Tiny ImageNet」は200分類ですが、ImageNetで学習済みのモデルは1000分類の出力になっているので、最後の全結合層の出力も200次元に修正します。

# ライブラリのインポート
import torch
from torch import nn
import torchvision.models as models

# GPU, CPUの設定
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")

# 学習済みResNet18の読み込み、全結合層の出力を200次元に変更
model = models.resnet18(pretrained = True)
num_ftrs = model.fc.in_features
model.fc = nn.Linear(num_ftrs, 200)
model = model.to(device)

# Global Average Pooling層の出力も取得できるモデルを作成
class SplittedResNet18(nn.Module):
    def __init__(self, resnet18):
        super().__init__()
        self.cnn = nn.Sequential(*list(resnet18.children())[:-1])
        self.flatten = nn.Flatten()
        self.fc = resnet18.fc

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        representation = self.flatten(self.cnn(x))
        output = self.fc(representation)
        return representation, output

# モデルのインスタンスを生成
splitted_model = SplittedResNet18(model)

これで全結合層からの出力とGlobal Average Pooling層からの出力の両方を取得するモデルを構築することができます。返り値の「representation」がGlobal Average Pooling層、「output」が全結合層からの出力となっています。

###損失関数の定義
OS Regularizationを用いた学習で使用する損失関数を定義します。

# ライブラリのインポート
import torch.nn.functional as F
from torch import linalg as LA

# 損失関数の定義
class CrossEntropyOSLoss(nn.Module):
    def __init__(self, regularization_param):
        super().__init__()
        self.Cross_Entropy_Loss = nn.CrossEntropyLoss()
        self.alpha = regularization_param

    def forward(self, output, representation, target):

        # 通常のクロスエントロピー誤差
        CEL_value = self.Cross_Entropy_Loss(output, target)

        # Orthogonal Sphere Regularization
        normalized_representation = F.normalize(representation, p = 2, dim = 1)
        OS_value = torch.add(
            torch.matmul(torch.t(normalized_representation), normalized_representation), 
            torch.eye(normalized_representation.size()[1], device = device), 
            alpha = -1
        )
        OS_value = self.alpha*LA.norm(OS_value, ord = "fro")

        return CEL_value + OS_value

# 損失関数のインスタンスを生成
alpha = 0.01 # 正則化パラメータ
loss_func = CrossEntropyOSLoss(alpha)

ここで定義した損失関数に全結合層からの出力、Global Average Pooling層からの出力、正解ラベルを入力することで損失の値を計算することができます。これでモデルと損失関数を準備できたので、後は普通に学習を行えばOKです。

精度比較

正則化パラメータを$\alpha = 0$（普通のResNet18）と$\alpha = 0.01$で30エポックの学習を行い、結果を比較します。以下にエポック毎のAccuracyの推移を示しています。

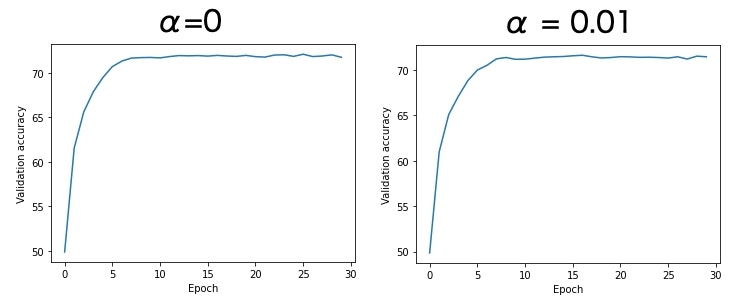
30エポックで学習は収束しているようです。最も良いときのAccuracyは普通のResNet18が72.12%、$\alpha = 0.01$として正則化を行なったモデルが72.30%でした。正則化を行なった方がAccuracyが0.18ポイント高いですが、分類精度に大きな差はなさそうです。

Grad-CAMによる可視化

以下のコアラの画像を例にGrad-CAMによる可視化を行なって、モデルが画像のどこを見て分類を行なっているかを確認してみます。コアラって言われないとコアラに見えないな・・・。

Grad-CAMで可視化した結果を見てみると、明らかに正則化を行なったモデルの方がよりコアラに集中して画像の認識を行なっていることがわかります。その結果、正則化なしのモデルでは「崖」と判定されていた画像を「コアラ」と正しく分類できるようになっています。背景の空の部分の重要度が減少したことが良い効果をもたらした感じでしょうか。

終わりに

Orthogonal Sphere Regularizationを試してみましたがなかなか良い結果を得ることができました。正則化の有無で全体的なモデルの精度はあまり変わりませんでしたが、背景に偏りのあるデータで実験してみるとまた違った結果になるかもしれません。実装するのも簡単なので余裕があればちょっと試してみても良いかも。

参考文献

・Orthogonal Sphere Regularizationの論文→https://arxiv.org/abs/2009.10762
・Grad-CAMの実装→https://axa.biopapyrus.jp/deep-learning/object-classification/pytorch-gradcam.html