Go to Qiita Advent Calendar 2024 Top
LoginSignup
7
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@tabintone(Komatsu)

分散分析の平方和のタイプについてまとめた

Last updated at Posted at 2021-01-01

はじめに

2要因以上のアンバランスなデータの分散分析をする場合、平方和の計算にはいくつかの方法があります。SASのGLM procedure1では「type I」「type II」「type III」「type IV」の4種類から選べるみたいなので、この4種類がメジャーな方法なんだと思います。今回はその中でtype I〜type IIIの違いについて二元配置分散分析を例にして勉強したことをまとめておくことにします。

アンバランスなデータ

アンバランスなデータとは以下のようにセルによっての観測値の数が異なるデータのことです。要因Aと要因Bにそれぞれ２つの水準がある以下の表のようなデータを考えます。$A_2B_1$のセルには観測値が2つありますが、それ以外のセルには値が一つしかありません。

$B_1$ $B_2$
$A_1$ $1$ $13$
$A_2$ $5,8$ $2$

全てのセルで観測値の数が同じ（バランスのとれたデータ）であればどのタイプの平方和を選んでも同じ分散分析の結果が得られます。しかし、現実のデータはアンバランスなデータの方が多いと思うので、分散分析を行うときは平方和のタイプを選択する必要があります。

平方和の分解

分散分析は正規線形モデルなので、観測値のベクトル$\boldsymbol{y}$、デザイン行列$\boldsymbol{X}$、未知パラメータのベクトル$\boldsymbol{\theta}$、成分が全て独立に正規分布$N(0, \sigma^2)$に従う誤差のベクトル$\boldsymbol{\epsilon}$を用いて以下のように表現できます。

\boldsymbol{y}=\boldsymbol{X}\boldsymbol{\theta}+\boldsymbol{\epsilon}

未知パラメータの最小二乗推定量は

\boldsymbol{\hat{\theta}}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}

で求めることができるので、残差平方和$SS_e$は残差ベクトル$\boldsymbol{\hat{\epsilon}}$を用いて

\displaylines{SS_e=\boldsymbol{\hat{\epsilon}}^T\boldsymbol{\hat{\epsilon}}\hspace{83pt}\\\
\hspace{17pt}=(\boldsymbol{y}-\boldsymbol{\hat{y}})^T(\boldsymbol{y}-\boldsymbol{\hat{y}})\hspace{31pt}\\\
\hspace{20pt}=(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\theta}})^T(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\hat{\theta}})\hspace{17pt}\\\
\hspace{29pt}=\boldsymbol{y}^T\boldsymbol{y}-\boldsymbol{y}^T\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}}

のように表すことができます。$\boldsymbol{y}^T\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}$の部分はデザイン行列が含まれているので、モデルにどのようなパラメータが入っているかによって値がかわります。そこで、モデルに含まれるパラメータを一緒に書いて$SS(\boldsymbol{\theta})$と表すことにします。そうすると、総平方和$SS_T=\boldsymbol{y}^T\boldsymbol{y}$について以下のような等式が成り立ちます。2

SS_T=SS(\boldsymbol{\theta})+SS_e

総平方和$SS_T$を残差平方和$SS_e$とそれ以外の部分$SS(\boldsymbol{\theta})$に分けています。この$SS(\boldsymbol{\theta})$はモデル平方和と呼ばれています。総平方和$SS_T$の値は常に一定ですが、どのようなモデルを使用するかによって総平方和に占める残差平方和$SS_e$とモデル平方和$SS(\boldsymbol{\theta})$の割合は変わってきます。

分散分析モデルをイメージすると、$SS(\boldsymbol{\theta})$はさらにモデルに含まれる要因毎に分解できそうです。このモデル平方和の分解方法の違いが平方和のタイプになっています。

一元配置分散分析

まずは一つの要因Aをもつ一元配置分散分析モデルを例に平方和の分解を考えます。データの総数を$N$とします。まず、要因Aの水準が含まれていないモデル①と要因Aの水準が含まれているモデル②を考えます。モデル②にはいま考えている全ての効果が含まれているのでフルモデル、モデル①は要因Aの効果が含まれていないので縮小モデルと呼ばれます。

 y_{ij}=\mu+\epsilon_{ij}\hspace{1cm}\cdots \hspace{1cm}モデル①

 \hspace{1cm}y_{ij}=\mu+\alpha_i+\epsilon_{ij}\hspace{1cm}\cdots \hspace{1cm}モデル②

モデル①は$\alpha_i$が消えているので水準によらず平均が同じ、モデル②は要因Aの水準によって平均が異なる、というモデルになっています。モデル②のデザイン行列を$\boldsymbol{X}$、モデル①のデザイン行列を$\boldsymbol{1}$（全ての成分が1のN×1行列）とすると、モデル平方和はそれぞれ、

 SS(\mu)=(\frac{1}{N})\boldsymbol{y}^T\boldsymbol{J}_N\boldsymbol{y}　\hspace{1cm}\cdots \hspace{1cm}モデル①

 SS(\mu,\boldsymbol{\alpha})=\boldsymbol{y}^T\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}\hspace{1cm}\cdots \hspace{1cm}モデル②

と書くことができます。$\boldsymbol{J_N}$は全ての成分が1のN次正方行列です。しかし、分散分析モデルでは$\boldsymbol{X}^T\boldsymbol{X}$が正則ではないので計算することができません。解決策としてモデルに制約条件を入れてデザイン行列を書きかえる、一般化逆行列を用いるといった方法がありますが、今回は前者の方法で進めます。制約条件として零和制約$\sum_{}{}\alpha_i=0$を入れるとデザイン行列は以下のように書きかえることができます。例として、要因の水準の数が2、水準1の観測値数が2、水準2の観測値数が3の簡単なデータを想定します。

\begin{pmatrix}
1 & 1 & 0 \\
1 & 1 & 0 \\
1 & 0 & 1\\
1 & 0 & 1\\
1 & 0 & 1
\end{pmatrix}
\Longrightarrow
\begin{pmatrix}
1 & 1  \\
1 & 1  \\
1 & -1 \\
1 & -1 \\
1 & -1 
\end{pmatrix}

左の行列が制約条件を入れる前のデザイン行列、右が制約条件を入れた後のデザイン行列です。このようにモデルに制約条件を入れて書き換えたデザイン行列$\boldsymbol{X}$を用いると、$\boldsymbol{X}^T\boldsymbol{X}$が正則になってモデル平方和の計算を行えるようになります。

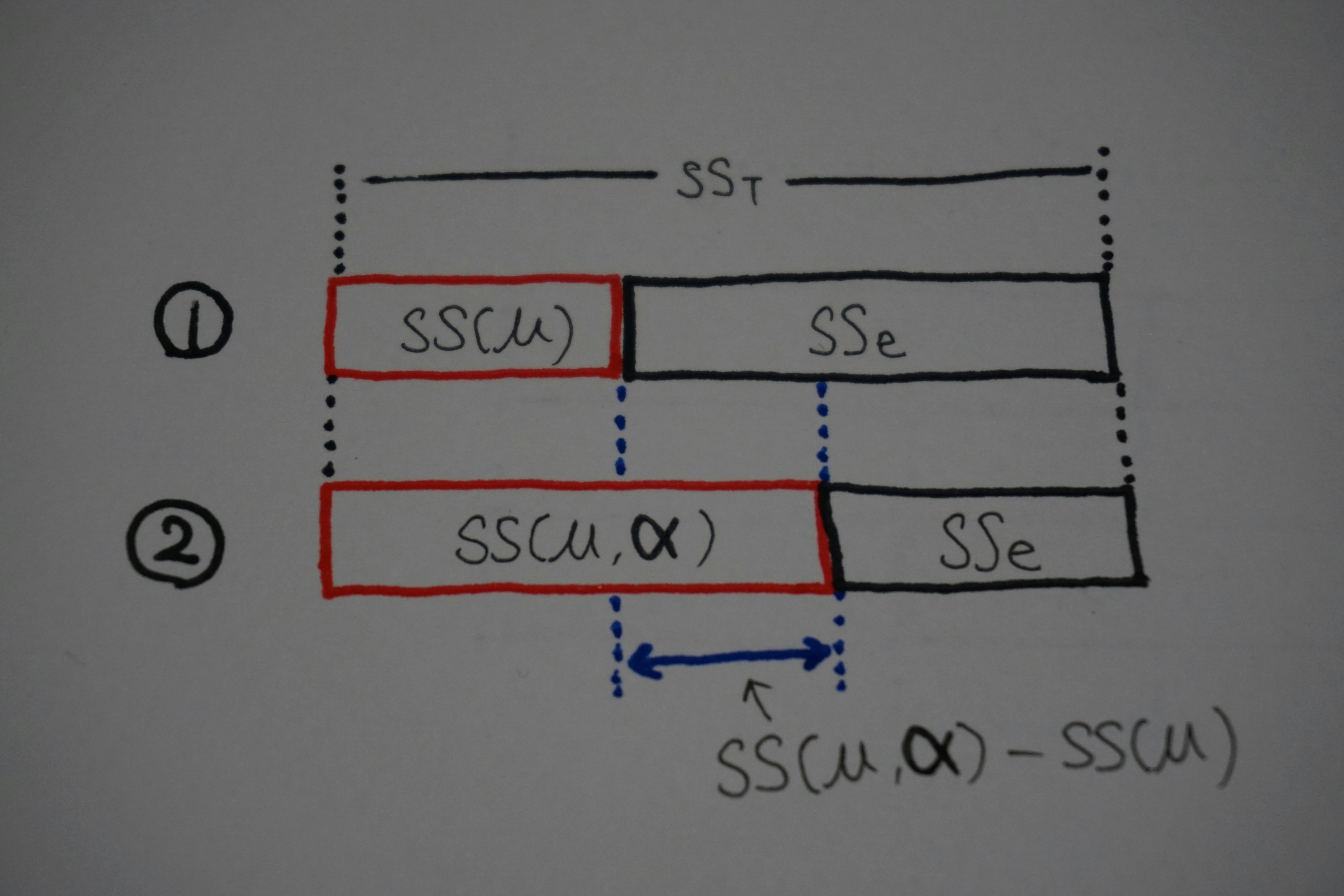
上記のように計算を行うことで、それぞれのモデルを用いて総平方和をモデル平方和と残差平方和に分解することができます。モデル①とモデル②の平方和の分解の違いは以下の絵のようになっています。

DSC00048.jpeg

$SS_T$はどんなモデルを使っても変わりませんが、モデル平方和はモデル①よりもモデル②の方が大きくなり、残差平方和は逆にモデル②の方が小さくなります。青矢印で示したモデル①とモデル②のモデル平方和の差分が要因Aの平方和（いわゆる群間平方和）です。上記の例では$SS(\mu,\boldsymbol{\alpha})-SS(\mu)$で計算することができます。なお、残差平方和はモデル②で計算します。

要因Aの平方和は「モデル①に要因Aを追加したときのモデル平方和の増加量」と考えることもできるし、「モデル②から要因Aを除いたときのモデル平方和の減少量」と考えることもできます。一元配置分散分析ではどちらでも同じことですが、アンバランスなデータで二元配置以上になると考え方によって平方和の値が変わってきます。前者の考え方で平方和を計算するのがType I、後者で計算するのがType IIやType IIIです。

ちなみに、分散分析で教科書とかによく出てくる、偏差平方和を群間平方和と残差平方和に分解する公式

\sum_{i}^{}\sum_{j}^{}(y_{ij}-\bar{y}_{..})^2=\sum_{i}^{}n_i(\bar{y}_{i.}-\bar{y}_{..})^2+\sum_{i}^{}\sum_{j}^{}(y_{ij}-\bar{y}_{i.})^2

はこれまでの表記に従うと、$SS_T-SS(\mu)=SS(\mu,\boldsymbol{\alpha})-SS(\mu)+SS_e$の計算を行うこととに相当しています。$SS_T-SS(\mu)$は平均調整総平方和と呼ばれるみたいです。

二元配置分散分析

以下のようなデータの二元配置分散分析を考えることにします。

$B_1$ $B_2$
$A_1$ $1$ $13$
$A_2$ $5,8$ $2$

まず、二元配置分散分析のフルモデル

y_{ijk}=\mu+\alpha_i+\beta_j+\gamma_{ij}+\epsilon_{ijk}

を考えます。$\alpha$は要因Aの効果、$\beta$は要因Bの効果、$\gamma$は交互作用を表しています。行列で表現すると、

\begin{pmatrix}
1\\
13\\
5\\
8\\
2\\
\end{pmatrix}=
\begin{pmatrix}
1 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0\\
1 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0\\
1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0\\
1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0\\
1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}
\mu\\
\alpha_1\\
\alpha_2\\
\beta_1\\
\beta_2\\
\gamma_{11}\\
\gamma_{12}\\
\gamma_{21}\\
\gamma_{22}\\
\end{pmatrix}
+\begin{pmatrix}
\epsilon_{111}\\
\epsilon_{121}\\
\epsilon_{211}\\
\epsilon_{212}\\
\epsilon_{221}\\
\end{pmatrix}

と書くことができます。一元配置のときと同様に制約条件を入れてデザイン行列を書き換えます。二元配置では$\sum_{}{}\alpha_i=0$, $\sum_{}{}\beta_j=0$, $\sum_{j}{}\gamma_{ij}=0$, $\sum_{i}{}\gamma_{ij}=0$を考えます。この制約条件によって、$\alpha_2=-\alpha_1$, $\beta_2 = -\beta_1$, $\gamma_{11}=-\gamma_{12}=-\gamma_{21}=\gamma_{22}$となるので、モデルの未知パラメータが$\mu, \alpha_1, \beta_1, \gamma_{11}$の4つに減ります。そうするとデザイン行列は以下のように書きかえることができます。

\boldsymbol{X}=
\begin{pmatrix}
1 & 1 & 1 & 1\\
1 & 1 & -1 & -1\\
1 & -1 & 1 & -1\\
1 & -1 & 1 & -1\\
1 & -1 & -1 & 1
\end{pmatrix}

このデザイン行列の1列目〜4列目がそれぞれ$\mu, \alpha_1, \beta_1, \gamma_{11}$に対応する列になっています。ここから一元配置のときと同じように縮小モデルを考えます。二元配置では以下のようなモデルとモデル平方和を考えます。

モデル（誤差項省略） モデル平方和 記号 モデル平方和の値
$y_{ijk}=\mu$ $(\frac{1}{N})\boldsymbol{y}^T\boldsymbol{J}_N\boldsymbol{y}$ $SS(\mu)$ $168.2$
$y_{ijk}=\mu+\alpha_i$ $\boldsymbol{y}^T\boldsymbol{X_{\mu\alpha}}(\boldsymbol{X_{\mu\alpha}}^T\boldsymbol{X_{\mu\alpha}})^{-1}\boldsymbol{X_{\mu\alpha}}^T\boldsymbol{y}$ $SS(\mu, \boldsymbol{\alpha})$ $173$
$y_{ijk}=\mu+\beta_j$ $\boldsymbol{y}^T\boldsymbol{X_{\mu\beta}}(\boldsymbol{X_{\mu\beta}}^T\boldsymbol{X_{\mu\beta}})^{-1}\boldsymbol{X_{\mu\beta}}^T\boldsymbol{y}$ $SS(\mu, \boldsymbol{\beta})$ $177.83333$
$y_{ijk}=\mu+\alpha_i+\beta_j$ $\boldsymbol{y}^T\boldsymbol{X_{\mu\alpha\beta}}(\boldsymbol{X_{\mu\alpha\beta}}^T\boldsymbol{X_{\mu\alpha\beta}})^{-1}\boldsymbol{X_{\mu\alpha\beta}}^T\boldsymbol{y}$ $SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta})$ $180.71428$
$y_{ijk}=\mu+\alpha_i+\gamma_{ij}$ $\boldsymbol{y}^T\boldsymbol{X_{\mu\alpha\gamma}}(\boldsymbol{X_{\mu\alpha\gamma}}^T\boldsymbol{X_{\mu\alpha\gamma}})^{-1}\boldsymbol{X_{\mu\alpha\gamma}}^T\boldsymbol{y}$ $SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\gamma})$ $242.42857$
$y_{ijk}=\mu+\beta_i+\gamma_{ij}$ $\boldsymbol{y}^T\boldsymbol{X_{\mu\beta\gamma}}(\boldsymbol{X_{\mu\beta\gamma}}^T\boldsymbol{X_{\mu\beta\gamma}})^{-1}\boldsymbol{X_{\mu\beta\gamma}}^T\boldsymbol{y}$ $SS(\mu, \boldsymbol{\beta}, \boldsymbol{\gamma})$ $249.85714$
$y_{ijk}=\mu+\alpha_i+\beta_j+\gamma_{ij}$ $\boldsymbol{y}^T\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}$ $SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})$ $258.5$

表の一番下がフルモデルで、それ以外が縮小モデルになっています。縮小モデルのデザイン行列は$\boldsymbol{X}$からモデルに含まれるパラメータに対応する列以外の列を削除した行列です。例えば、$\boldsymbol{X_{\mu\alpha}}$はモデルに含まれるパラメータ$\mu, \alpha_1$に対応する列である1列目、2列目を取り出した

\boldsymbol{X_{\mu\alpha}}=
\begin{pmatrix}
1 & 1 \\
1 & 1 \\
1 & -1 \\
1 & -1 \\
1 & -1 
\end{pmatrix}

のような感じです。各モデル平方和の値は以下のように計算しています。このモデル平方和を使って各タイプの平方和を計算していきます。

python
import numpy as np
import pandas as pd

#データセット
df = pd.DataFrame({'A':['A1','A1','A2','A2','A2'],
                   'B':['B1','B2','B1','B1','B2'],
                   'Value':[1,13,5,8,2]})

#測定値ベクトルとデザイン行列（フルモデル）
y = np.matrix(df['Value']).T
X = np.matrix([[1,1,1,1],
               [1,1,-1,-1],
               [1,-1,1,-1],
               [1,-1,1,-1],
               [1,-1,-1,1]])

#各モデル平方和の計算
SS_mu = y.T*X[:,0]*np.linalg.inv(X[:,0].T*X[:,0])*X[:,0].T*y
SS_mu_a = y.T*X[:,0:2]*np.linalg.inv(X[:,0:2].T*X[:,0:2])*X[:,0:2].T*y
SS_mu_b = y.T*X[:,0:3:2]*np.linalg.inv(X[:,0:3:2].T*X[:,0:3:2])*X[:,0:3:2].T*y
SS_mu_a_b = y.T*X[:,0:3]*np.linalg.inv(X[:,0:3].T*X[:,0:3])*X[:,0:3].T*y
SS_mu_a_g = y.T*X[:,[0,1,3]]*np.linalg.inv(X[:,[0,1,3]].T*X[:,[0,1,3]])*X[:,[0,1,3]].T*y
SS_mu_b_g = y.T*X[:,[0,2,3]]*np.linalg.inv(X[:,[0,2,3]].T*X[:,[0,2,3]])*X[:,[0,2,3]].T*y
SS_mu_a_b_g = y.T*X*np.linalg.inv(X.T*X)*X.T*y

Type I

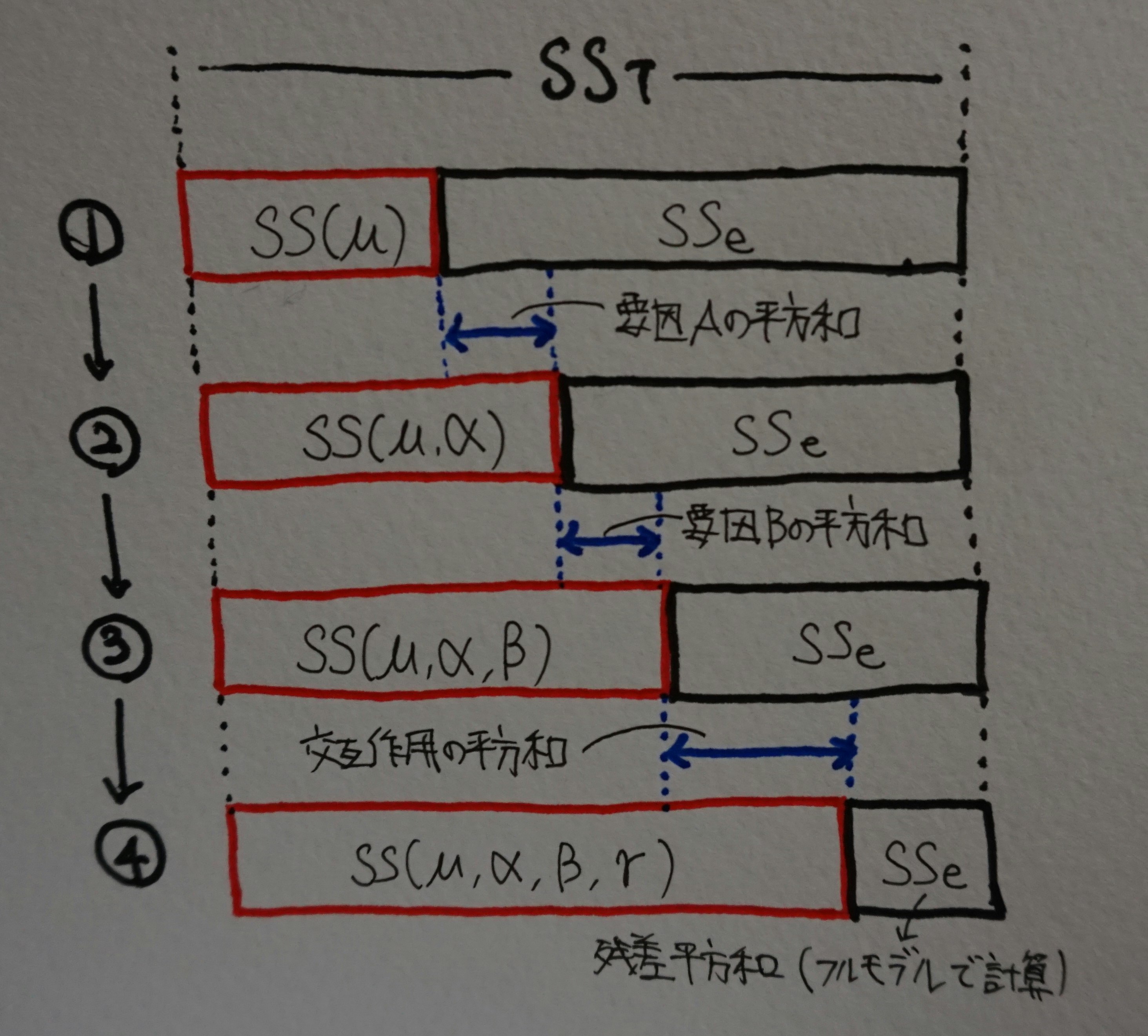
Type I平方和は以下のように計算します。type Iは要因をモデルに入れる順番に依存するので、要因はA→B→交互作用の順にモデルに入れることにします。

\displaylines{要因Aの平方和=SS(\mu, \boldsymbol{\alpha})-SS(\mu)\\
要因Bの平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta})-SS(\mu, \boldsymbol{\alpha})\\
交互作用の平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})-SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta})\\
残差平方和=SS_T-SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})}

総平均$\mu$のみのモデルからスタートして、要因を順番にモデルに入れていったときのモデル平方和の増加量を要因の平方和とするのがtype I平方和です。以下の絵のようなイメージです。

DSC00054.JPG

実際にtype I平方和を計算してみます。すでに各モデル平方和は先ほど計算済なので、その値を使います。

python
# Type I SS
A = SS_mu_a - SS_mu
B = SS_mu_a_b - SS_mu_a
AB = SS_mu_a_b_g - SS_mu_a_b
Residual = y.T*y - SS_mu_a_b_g

print(A)
print(B)
print(AB)
print(Residual)

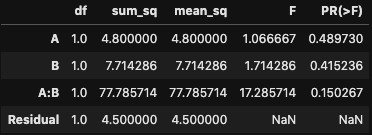
[[4.8]]         #要因Aの平方和
[[7.71428571]]  #要因Bの平方和
[[77.78571429]] #交互作用の平方和
[[4.5]]         #残差平方和

平方和の値が得られたのでstatsmodelsを使った分散分析と結果を比べてみます。

python
import statsmodels.formula.api as smf
import statsmodels.api as sm

model = smf.ols("Value ~ A*B", data = df).fit()
sm.stats.anova_lm(model, typ = 1)

スクリーンショット 2020-12-31 2.02.46.png

上の画像のsum_sq列の値と自分で計算した値を比べてみると一致していることがわかります。

type I平方和の性質として、①全ての平方和を足すと平均調整総平方和$SS_T-SS(\mu)$と一致する、②モデルに要因を入れる順番によって平方和の値が異なる、といった点が挙げられます。②についてはB→A→交互作用の順番にしてみると先ほどとは異なる値が得られることが確認できると思います。交互作用は最後にモデルに入れるので、順番を変えても交互作用の平方和の値は変化しません。また、残差平方和も同様に要因をモデルに入れる順番には依存しません。

Type II

Type II平方和は以下のように計算します。

\displaylines{要因Aの平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta})-SS(\mu, \boldsymbol{\beta})\\
要因Bの平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta})-SS(\mu, \boldsymbol{\alpha})\\
交互作用の平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})-SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta})\\
残差平方和=SS_T-SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})}

type IIでは全ての主効果が入ったモデルからスタートして、モデルからある要因を除いたときのモデル平方和の減少量を計算しています。交互作用と残差平方和についてはtype Iと全く同じです。以下の絵のようなイメージです。
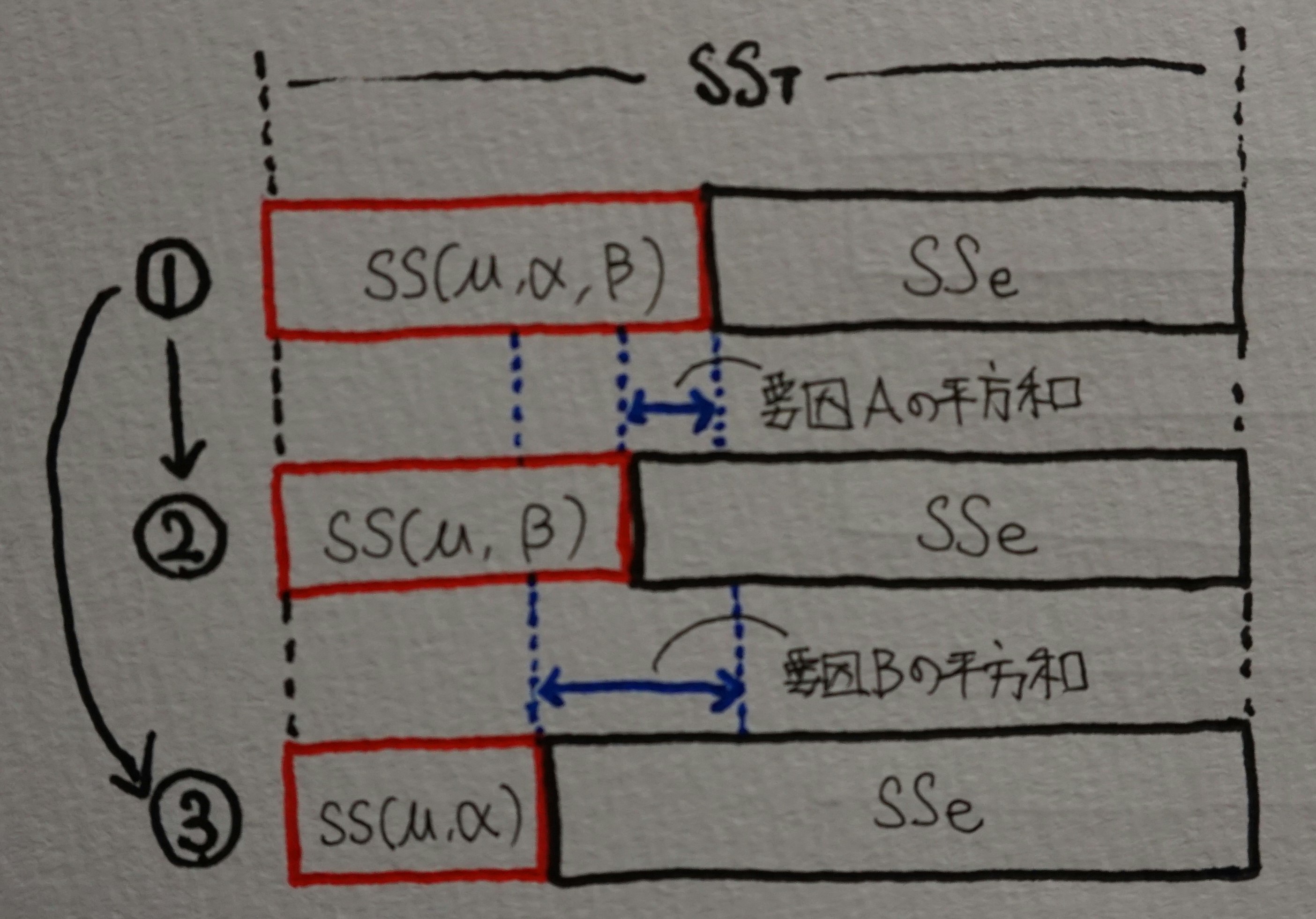
DSC00055.JPG

実際に平方和を計算してみます。

python
# Type II SS
A = SS_mu_a_b - SS_mu_b
B = SS_mu_a_b - SS_mu_a
AB = SS_mu_a_b_g - SS_mu_a_b
Residual = y.T*y - SS_mu_a_b_g

print(A)
print(B)
print(AB)
print(Residual)

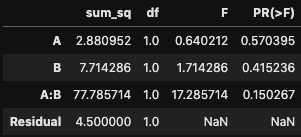
[[2.88095238]]  #要因Aの平方和
[[7.71428571]]  #要因Bの平方和
[[77.78571429]] #交互作用の平方和
[[4.5]]         #残差平方和

statsmodelsを使った分散分析も行います。

python
model = smf.ols("Value ~ A*B", data = df).fit()
sm.stats.anova_lm(model, typ = 2)

スクリーンショット 2020-12-31 20.37.21.png

これも自分で計算した値を比べてみるとちゃんと一致していることがわかります。

計算式からわかる通り、type IIはモデルに要因を入れる順番に依存しません。要因Aの平方和を先に計算しても、要因Bから計算しても得られる平方和の値は同じです。また、今回のデータで全ての平方和を足すと$92.88$になります。平均調整総平方和（偏差平方和）は$94.8$なので、type IIでは全ての平方和の和と平均調整総平方和が一致しないことがわかります。

Type III

Type III平方和は以下のように計算します。

\displaylines{要因Aの平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})-SS(\mu, \boldsymbol{\beta}, \boldsymbol{\gamma})\\
要因Bの平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})-SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\gamma})\\
交互作用の平方和=SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})-SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta})\\
残差平方和=SS_T-SS(\mu, \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma})}

type IIIでは二元配置のフルモデルからスタートして、モデルからある要因を除いたときのモデル平方和の減少量を計算しています。交互作用と残差平方和についてはtype I、IIと全く同じになっています。type IIIは主効果の平方和を計算するときに交互作用でも調整されることになります。絵はtype IIとほぼ同じなので省略です。

実際に平方和を計算してみます。

python
# Type III SS
A = SS_mu_a_b_g - SS_mu_b_g
B = SS_mu_a_b_g - SS_mu_a_g
AB = SS_mu_a_b_g - SS_mu_a_b
Residual = y.T*y - SS_mu_a_b_g

print(A)
print(B)
print(AB)
print(Residual)

[[8.64285714]]  #要因Aの平方和
[[16.07142857]] #要因Bの平方和
[[77.78571429]] #交互作用の平方和
[[4.5]]         #残差平方和

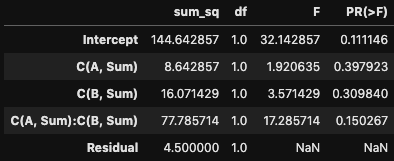
statsmodelsを使った分散分析も行いましょう。

python
model = smf.ols("Value ~ C(A, Sum)*C(B, Sum)", data = df).fit()
sm.stats.anova_lm(model, typ = 3)

スクリーンショット 2020-12-31 23.52.55.png

これも自分で計算した値を比べてみると、無事に一致していることがわかります。3

type IIIもtype IIと同様にモデルに要因を入れる順番に依存しません。今回のデータで全ての平方和を足すと$107$になります。平均調整総平方和（偏差平方和）は$94.8$なので、type IIIも全ての平方和の和と平均調整総平方和が一致しないことがわかります。計算式から分かる通り、モデルに交互作用を含まない場合はtype IIIとtype IIは一致します。

type IIとtype IIIの違い

もう少しtype IIとtype IIIの違いを見てみます。これまで制約条件として$\sum_{}{}\alpha_i=0$, $\sum_{}{}\beta_j=0$, $\sum_{j}{}\gamma_{ij}=0$, $\sum_{i}{}\gamma_{ij}=0$を考えていました。ここで、交互作用に関する制約条件を$\sum_{j}{}n_{ij}\gamma_{ij}=0$, $\sum_{i}{}n_{ij}\gamma_{ij}=0$に変更します。$n_{ij}$はセル$A_iB_j$の観測値の数です。今回のデータでは$n_{21}=2$でそれ以外は全て1になります。この制約条件は交互作用にデータの数で重みをつけていることになります。

この制約条件でパラメータを消去すると、$\gamma_{12}=-\gamma_{11}$、$\gamma_{21}=-(1/2)\gamma_{11}$、$\gamma_{22}=\gamma_{11}$になるので、制約条件を入れた後のデザイン行列$\boldsymbol{X}$は

\boldsymbol{X}=
\begin{pmatrix}
1 & 1 & 1 & 1\\
1 & 1 & -1 & -1\\
1 & -1 & 1 & -0.5\\
1 & -1 & 1 & -0.5\\
1 & -1 & -1 & 1
\end{pmatrix}

になります。このデザイン行列を使って先ほどのType IIIの方法で平方和の計算を行います。

python
#デザイン行列（フルモデル）
y = np.matrix(df['Value']).T
X = np.matrix([[1,1,1,1],
               [1,1,-1,-1],
               [1,-1,1,-0.5],
               [1,-1,1,-0.5],
               [1,-1,-1,1]])

#各モデル平方和の計算
SS_mu_a_b = y.T*X[:,0:3]*np.linalg.inv(X[:,0:3].T*X[:,0:3])*X[:,0:3].T*y
SS_mu_a_g = y.T*X[:,[0,1,3]]*np.linalg.inv(X[:,[0,1,3]].T*X[:,[0,1,3]])*X[:,[0,1,3]].T*y
SS_mu_b_g = y.T*X[:,[0,2,3]]*np.linalg.inv(X[:,[0,2,3]].T*X[:,[0,2,3]])*X[:,[0,2,3]].T*y
SS_mu_a_b_g = y.T*X*np.linalg.inv(X.T*X)*X.T*y

# Type IIIの方法で平方和を計算
A = SS_mu_a_b_g - SS_mu_b_g
B = SS_mu_a_b_g - SS_mu_a_g
AB = SS_mu_a_b_g - SS_mu_a_b
Residual = y.T*y - SS_mu_a_b_g

print(A)
print(B)
print(AB)
print(Residual)

[[2.88095238]]  #要因Aの平方和
[[7.71428571]]  #要因Bの平方和
[[77.78571429]] #交互作用の平方和
[[4.5]]         #残差平方和

この結果を見てみると先ほどのtype IIの結果と同じになっています。type IIIの計算方法でも制約条件を変えることによってtype IIの結果を得ることができます。計算方法をtype IIIの方法で固定すると、交互作用にセルのデータ数で重みをつけた制約条件を考えた平方和がtype II,データ数で重みをつけない制約条件を考えた平方和がtype IIIになります。このようにtype IIとtype IIIの違いは制約条件の違いと考えることもできます。

平方和の使い分け

平方和のタイプの使い分けですが、要因間に順序関係がある時はtype Iを使うことも選択肢に入るでしょう。type IIとtype IIIについては、アンバランスの度合いが大きいときはセルのデータ数を考慮するtype IIの方が良いような気がしてきます。ただ、type IIとtype IIIのどちらが良いかは色々な議論があるようです。分野でよく使われている方を使うとか、両方計算してみて結果を比べてみたりするのが無難なところでしょうか。

参考文献

①https://www.researchgate.net/publication/341426272_fensanfenxiniokeru3tsutaipunopingfanghe_-_Type_I_II_III_SS_-_Three_types_of_SS_in_ANOVA_-_yitengyaoer_-_KRyanjiuhui_2005nian9yue15ri
②https://www.sas.com/content/dam/SAS/ja_jp/doc/event/sas-user-groups/usergroups11-p-04.pdf

  1. SASで分散分析するときに使うやつです。 ↩

  2. ここでの総平方和は単に観測値の二乗和です。偏差平方和ではありません。 ↩

  3. type III平方和を使うときには「C(A, Sum)」のように要因の変数を記述しないと変な結果になります。これで1時間くらい悩みました。 ↩

7
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?