分位点回帰の基本的なところ

Last updated at 2024-02-22Posted at 2023-07-13

はじめに

最近、分位点回帰を扱うことがあったので基本的なところを整理しておきます。通常の回帰分析では「説明変数で条件付けた目的変数の条件付き期待値」を扱うのに対して、分位点回帰では「説明変数で条件付けた目的変数の条件付き分位点」を扱うことが可能になります。

最適化問題としての分位点推定

分位点回帰を行う前にデータの分位点の推定を最適化問題として扱うことを考えます。まずは分位点の推定の際に必要な関数を以下に定義しておきます。

累積分布関数及び分位点関数

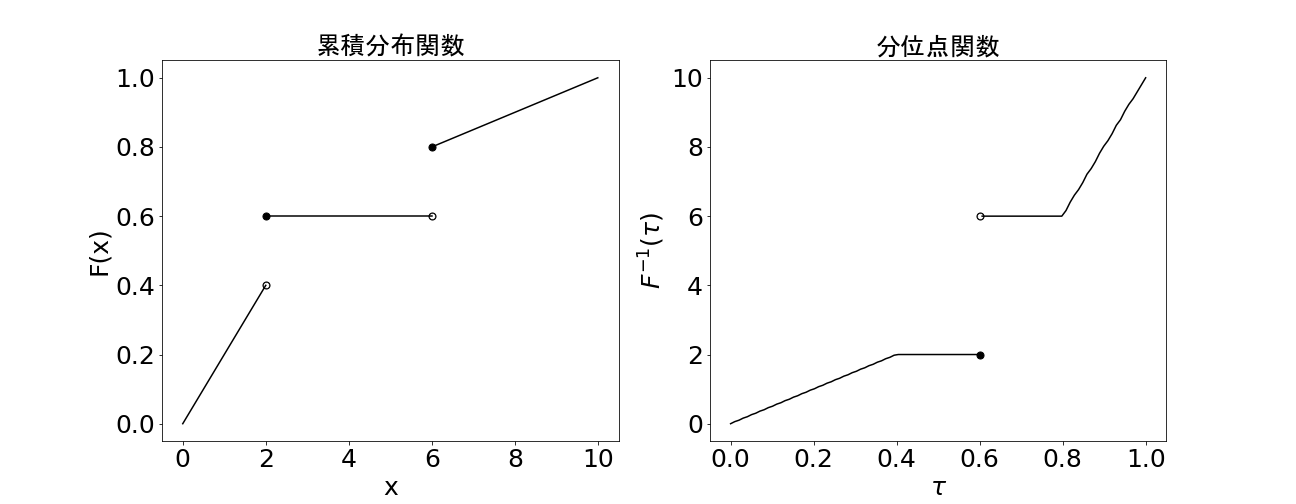
確率変数$X$の累積分布関数$F(x)$及びその逆関数$F^{-1}(\tau)$を以下のように定義します。

F(x)=P(X \leq x)\\

\hspace{35pt}F^{-1}(\tau)=\inf\{x|F(x)\geq\tau\}\hspace{15pt} (0<\tau<1)

$F^{-1}(\tau)$は$0\sim1$の入力に対して分位点を返すような関数なので分位点関数と呼ばれています。

仮に累積分布分布関数が上の左側のようなグラフのとき、分位点関数は右側のようなグラフになります。

Pinball Loss

次にPinball Lossと呼ばれている関数を定義しておきます。

L_{\tau}(r)=r\{\tau-I(r<0)\}=\left\{
\begin{array}{ll}
r(\tau-1) & (r<0) \\
r\tau & (r\geq0)
\end{array}
\right.

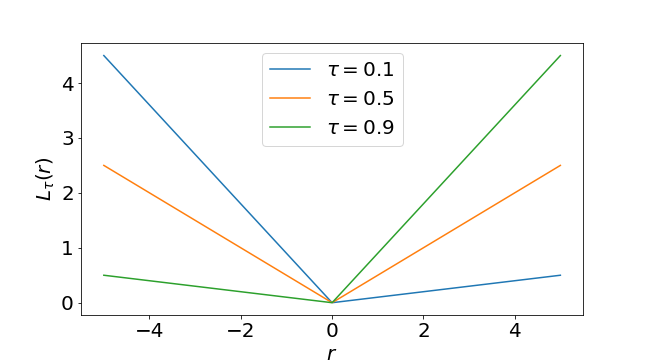
ここで$I(\cdot)$は入力が真であれば$1$、偽であれば$0$を返す指示関数です。グラフにすると以下のような形になっています。

分位点の推定

準備ができたので分位点の推定を最適化問題として扱うことを考えます。$X$を確率変数、$\mathbb{E}[\cdot]$を期待値、$\tau$を$0<\tau<1$を満たす実数とします。このとき、

\mathbb{E}[L_{\tau}(X-\mu)]\hspace{10pt}\cdot\cdot\cdot\hspace{10pt}(1)

を最小化する$\mu$は$X$の$\tau$分位数であることが知られています。それを確認するには$(1)$式を$\mu$で微分して$0$とおいた方程式を$\mu$について解けば良いです。まずは$(1)$式を期待値及びPinball Lossの定義に従って式を変形していくと、

\mathbb{E}[L_{\tau}(X-\mu)]

=\int_{-\infty}^{\infty}L_{\tau}(x-\mu)dF(x)

=(\tau-1)\int_{-\infty}^{\mu}(x-\mu)dF(x)+\tau\int_{\mu}^{\infty}(x-\mu)dF(x)

となります。これを$\mu$で微分して$0$とおくと、

(1-\tau)\int_{-\infty}^{\mu}dF(x)+\tau\int_{\mu}^{\infty}dF(x)=0

F(\mu)-\tau=0

F(\mu)=\tau

\mu=F^{-1}(\tau)

となるので、$(1)$式を最小化する$\mu$は$X$の$\tau$分位数であることが分かります。これは$L_{\tau}(X-\mu)$を以下のように書き直してみると感覚的にも分かり易くなります。

L_{\tau}(X-\mu)=\left\{
\begin{array}{ll}
(1-\tau)|X-\mu| & (X<\mu) \\
\tau|X-\mu| & (X\geq\mu)
\end{array}
\right.

仮に$\tau=0.1$とすると

L_{0.1}(X-\mu)=\left\{
\begin{array}{ll}
0.9|X-\mu| & (X<\mu) \\
0.1|X-\mu| & (X\geq\mu)
\end{array}
\right.

となるなります。データ$X$を固定して$\mu$を動かすことを考えると、$\mu$より小さいデータに対しては$|X-\mu|$に$0.9$が掛け算されて、$\mu$よりも大きいデータに対しては$|X-\mu|$に$0.1$が掛け算されるので、$\mu$より小さいデータの誤差に対する重みは$\mu$よりも大きいデータよりも$9$倍大きくなります。したがって、$L_{0.1}(X-\mu)$を最小化するには$\mu$を$0.1$分位数あたりの値にして$\mu$より小さいデータを減らすことで誤差の大きさと重みの差のバランスを取らなければならないことが分かります。同様に$\tau=0.9$のときは$\mu$をデータの中でもかなり大きめにする必要があり、$\tau=0.5$のときは$\mu$をデータの真ん中ぐらいの値にしなければならないことが分かると思います。

ここで紹介したのは分位数の点推定を最適化問題として行うための性質でしたが、この性質は回帰分析にもそのまま適用することができます。

分位点回帰

特徴量$\boldsymbol{x}=(x_1,\ldots,x_p)^T$の値によって目的変数$Y$の分位点が変化するようなケースを考えます。そこで未知パラメータ${\boldsymbol{\mathstrut \theta}}$を持つ特徴量$\boldsymbol{x}$の関数を$g_{\boldsymbol{\theta}}(\boldsymbol{x})$として、$(1)$式のかわりに

\mathbb{E}[L_{\tau}(Y-g_{\boldsymbol{\theta}}(\boldsymbol{x}))]\hspace{10pt}\cdot\cdot\cdot\hspace{10pt}(2)

を最小化する$\boldsymbol{\theta}$を推定することにします。したがって、未知パラメータを$\boldsymbol{\theta}$の推定値$\hat{\boldsymbol{\mathstrut \theta}}$は

\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\hat{\boldsymbol{\theta}}=\argmin_{\boldsymbol{\theta}\in\mathbb{R}^p}\hspace{2pt}\mathbb{E}[L_{\tau}(Y-g_{\boldsymbol{\theta}}(\boldsymbol{x}))]

\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\hspace{68pt}\simeq\argmin_{\boldsymbol{\theta}\in\mathbb{R}^p}\sum_{i=1}^{N}L_{\tau}(y_i-g_{\boldsymbol{\theta}}(\boldsymbol{x}_i))\hspace{10pt}\cdot\cdot\cdot\hspace{10pt}(3)

のように表現することができます。このように未知パラメータを$\boldsymbol{\theta}$を推定することは説明変数$\boldsymbol{x}$が与えられた時の$Y$の条件付き分位点$F_Y^{-1}(\tau|\boldsymbol{x})$に対して、

F_Y^{-1}(\tau|\boldsymbol{x})=\inf\{y|F_Y(y|\boldsymbol{x})\geq\tau\}=g_{\boldsymbol{\theta}}(\boldsymbol{x})\hspace{15pt} (0<\tau<1)

のようなモデルを構築することを意味しています。これによって説明変数$\boldsymbol{x}$の値によって目的変数$Y$の分位点がどのように変化する記述したり分位点がどれくらいの値になるかを予測できるようになります。

分位点線形回帰

まずは分位回帰モデル$g_{\boldsymbol{\theta}}(\boldsymbol{x})$が未知パラメータ$\boldsymbol{\theta}$に対して線形な場合の分位点回帰を行います。この場合のモデルは

g_{\boldsymbol{\theta}}(\boldsymbol{x})=\boldsymbol{x}^T\boldsymbol{\theta}=x_1\theta_1+\cdots+x_p\theta_p

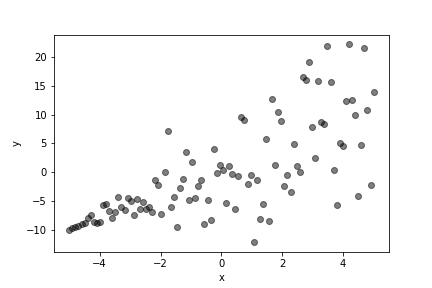
の形で表現されます。ここでは以下のようなサンプルデータに対して分位点回帰を行うことにします。

python

import pandas as pd
import numpy as np

# サンプルデータ作成
np.random.seed(seed=32)
x = np.linspace(-5, 5, 100)
y = np.random.normal(loc = 2*x, scale = [0.1*i for i, _ in enumerate(x)])
data = pd.DataFrame(np.stack([np.ones(100), x, y], 1), columns = ['X0', 'X1', 'Y'])

データセットはこんな感じ。

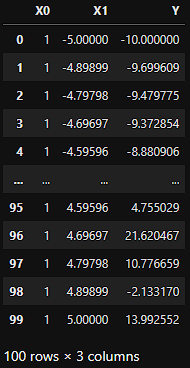
「X0」列と「X1」列が説明変数、「Y」列が目的変数の値です。「X0」列は切片を表す説明変数なのですべての値が$1$になっています。このデータに対するモデルは

g_{\boldsymbol{\theta}}(\boldsymbol{x})=\theta_0+x_1\theta_1

であり、推定する未知パラメータは切片$\theta_0$と$x_1$に対する回帰係数$\theta_1$の2つです。推定する分位点は$0.1, 0.5, 0.9$の3つにします。

scikit-learnでやる

scikit-learnには分位点回帰を行う「QuantileRegressor」クラスが用意されているのでこれを使います。

python

import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor

# データ準備
X = data[['X0', 'X1']].values
y = data['Y'].values

# 分位点回帰実行、回帰直線描画、回帰係数保存
fig, ax = plt.subplots(1, 1)
ax.scatter(data["X1"], data['Y'], color = 'black', alpha = 0.5)
coefficients = pd.DataFrame()
taus = [0.1, 0.5, 0.9]
for t in taus:
    # パラメータ推定
    model = QuantileRegressor(quantile = t, alpha = 0, fit_intercept = False)
    model.fit(X, y)
    # 回帰直線プロット
    ax.plot(X[:,1], model.predict(X), label = t)
    # 回帰係数保存
    temp_data = pd.DataFrame(model.coef_.reshape(1, -1), columns = ['theta0', 'theta1'])
    temp_data['tau'] = t
    coefficients = pd.concat([coefficients, temp_data])
ax.legend()
plt.show()

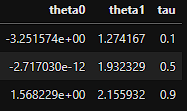
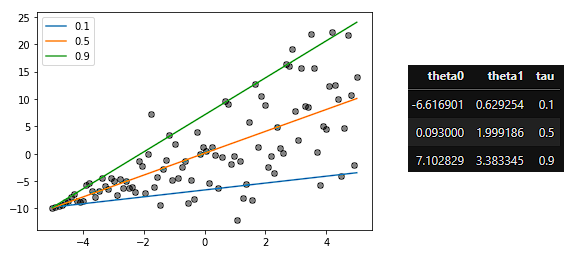
回帰直線と回帰係数は以下のようになりました。簡単にできて良い感じです。

未知パラメータの推定方法

分位点回帰のパラメータ推定はどのように行われているのでしょうか？QuantileRegressorのマニュアルを見てみると

と書いてあるのでどうやら線形計画問題として定式化してパラメータ推定が行われているようです。線形計画問題は以下のような標準形で表現される最小化問題です。

\newcommand{\min}{\mathop{\rm min}\limits}
\min_{\boldsymbol{z}}\hspace{2pt}\boldsymbol{c}^T\boldsymbol{z}\hspace{5pt}subject\hspace{2pt}to\hspace{5pt}A\boldsymbol{z}=\boldsymbol{b},\hspace{2pt}\boldsymbol{z}\geq\boldsymbol{0}

そこで、$(3)$式のパラメータ推定の定式化を線形計画問題の標準形に書き換えていきます。$(3)$式の中身は指示関数$I(\cdot)$を用いて、

\sum_{i=1}^{N}L_{\tau}(y_i-g_{\boldsymbol{\theta}}(\boldsymbol{x}_i))

=\sum_{i=1}^{N} \{\tau(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}\geq0)+(\tau-1)(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}<0)\}

=\sum_{i=1}^{N} \{\tau(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}\geq0)+(1-\tau)(-1)(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}<0)\}

と書くことができます。ここで、

u_i=\max(0, y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})=(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}\geq0)

v_i=\max\{0, -(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})\}=(-1)(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}<0)

と置けば、さらに式変形を進めることできて

\sum_{i=1}^{N} \{\tau(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}\geq0)+(1-\tau)(-1)(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})I(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}<0)\}

=\sum_{i=1}^{N}\{\tau u_i+(1-\tau)v_i\}

=\tau\boldsymbol{1}_N^T\boldsymbol{u}+(1-\tau)\boldsymbol{1}_N^T\boldsymbol{v}

となります。ここで、$\boldsymbol{1}_N$はすべての要素が$1$の$N\times1$ベクトル、$\boldsymbol{u},\boldsymbol{v}$はそれぞれ$u_i,v_i$を要素に持つ$N\times1$ベクトルです。$y_i-\boldsymbol{x}_i^T\boldsymbol{\theta}=u_i-v_i$なので$(3)$式は

\displaylines{\newcommand{\min}{\mathop{\rm min}\limits}
\min_{\boldsymbol{\theta},\boldsymbol{u}, \boldsymbol{v}}\hspace{2pt}\tau\boldsymbol{1}_N^T\boldsymbol{u}+(1-\tau)\boldsymbol{1}_N^T\boldsymbol{v}\hspace{5pt}\\
\hspace{28pt}subject\hspace{2pt}to\hspace{5pt}y_i=\boldsymbol{x}_i^T\boldsymbol{\theta}+u_i-v_i\hspace{5pt}(i=1,\ldots,N),\\
\hspace{19pt}\boldsymbol{u}\geq\boldsymbol{0},\hspace{3pt}\boldsymbol{v}\geq\boldsymbol{0}, \hspace{3pt}\boldsymbol{\theta}\in\mathbb{R}^p}

のように書き換えることができます。だんだん線形計画問題の標準形に近づいてきました。しかし、まだ$\boldsymbol{\theta}$に対する制約条件が非負になっていないのでもう少し変形を続けます。

\displaylines{\boldsymbol{\theta}^+=\begin{pmatrix}
{\theta_1}^+  \\
\vdots\\
{\theta_p}^+\\
\end{pmatrix}=\begin{pmatrix}
\max(0, \theta_1)  \\
\vdots\\
\max(0, \theta_p)\\
\end{pmatrix},
\hspace{10pt}
\boldsymbol{\theta}^-=\begin{pmatrix}
{\theta_1}^-  \\
\vdots\\
{\theta_p}^-\\
\end{pmatrix}=\begin{pmatrix}
\max(0, -\theta_1)  \\
\vdots\\
\max(0, -\theta_p)\\
\end{pmatrix}}

とすれば、$\boldsymbol{\theta}^+$と$\boldsymbol{\theta}^-$の各要素は非負であり、

\boldsymbol{\theta}=\boldsymbol{\theta}^+-\boldsymbol{\theta}^-

となります。これを用いれば目的の線形計画問題は

\newcommand{\min}{\mathop{\rm min}\limits}
\displaylines{\min_{\boldsymbol{\theta},\boldsymbol{u}, \boldsymbol{v}}\hspace{2pt}\tau\boldsymbol{1}_N^T\boldsymbol{u}+(1-\tau)\boldsymbol{1}_N^T\boldsymbol{v}\hspace{5pt}\\
\hspace{65pt}subject\hspace{2pt}to\hspace{5pt}y_i=\boldsymbol{x}_i^T(\boldsymbol{\theta}^+-\boldsymbol{\theta}^-)+u_i-v_i\hspace{5pt}(i=1,\ldots,N),\\
\hspace{60pt}\boldsymbol{u}\geq\boldsymbol{0},\hspace{3pt}\boldsymbol{v}\geq\boldsymbol{0}, \hspace{3pt}\boldsymbol{\theta}^+\geq\boldsymbol{0},\hspace{3pt}\boldsymbol{\theta}^-\geq\boldsymbol{0}}

のように書くことができます。これで標準形の条件は満たしていますが、もう少しきれいに整理することにします。

\boldsymbol{c}=\begin{pmatrix}
\boldsymbol{0}  \\
\boldsymbol{0}\\
\tau\boldsymbol{1}_N\\
(1-\tau)\boldsymbol{1}_N
\end{pmatrix},\hspace{5pt}
\boldsymbol{z}=\begin{pmatrix}
\boldsymbol{\theta}^+  \\
\boldsymbol{\theta}^-\\
\boldsymbol{u}\\
\boldsymbol{v}
\end{pmatrix}

とすれば線形計画問題の目的関数は

\tau\boldsymbol{1}_N^T\boldsymbol{u}+(1-\tau)\boldsymbol{1}_N^T\boldsymbol{v}\hspace{5pt}=\boldsymbol{c}^T\boldsymbol{z}

と書くことができます。ここで$\boldsymbol{0}$はすべての要素が$0$の$p\times1$ベクトルです。さらに

\boldsymbol{b}=\begin{pmatrix}
y_1  \\
\vdots\\
y_N\\
\end{pmatrix},
\hspace{5pt}
\boldsymbol{X}=\begin{pmatrix}
\boldsymbol{x}_1^T  \\
\vdots\\
\boldsymbol{x}_N^T\\
\end{pmatrix}

として、$\boldsymbol{X}$と$N$次単位行列$\boldsymbol{E}_N$を用いて

\boldsymbol{A}=(\boldsymbol{X},\hspace{2pt}-\boldsymbol{X},\hspace{2pt}\boldsymbol{E}_N,\hspace{2pt}-\boldsymbol{E}_N)

のような行列$\boldsymbol{A}$を作れば、線形計画問題の等号の制約条件は

\boldsymbol{A}\boldsymbol{z}=\boldsymbol{b}

と書くことができます。これらの記号を使って分位点回帰の線形計画問題を書くと以下のようになります。

\newcommand{\min}{\mathop{\rm min}\limits}
\min_{\boldsymbol{z}}\hspace{2pt}\boldsymbol{c}^T\boldsymbol{z}\hspace{5pt}subject\hspace{2pt}to\hspace{5pt}A\boldsymbol{z}=\boldsymbol{b},\hspace{2pt}\boldsymbol{z}\geq\boldsymbol{0}

この線形計画問題を解くことで、$\boldsymbol{\theta}^+,\boldsymbol{\theta}^-$の推定値$\hat{\boldsymbol{\theta}}^+,\hat{\boldsymbol{\theta}}^-$が得られるので、

\hat{\boldsymbol{\theta}}=\hat{\boldsymbol{\theta}}^+-\hat{\boldsymbol{\theta}}^-

の計算で未知パラメータの推定値$\hat{\boldsymbol{\mathstrut \theta}}$を求めることができます。それでは実際に線形計画問題を解いて分位点回帰の回帰係数を推定してみます。実際に線形計画問題を解くのはscipyに頼ります。

python

from scipy.optimize import linprog

# データ準備
X = data[['X0', 'X1']].values
y = data['Y'].values

# 分位点回帰実行、回帰係数保存
coefficients = pd.DataFrame()
taus = [0.1, 0.5, 0.9]
for t in taus:
    # 線形計画問題の行列を作成
    b = y.reshape(-1, 1)
    A = np.hstack([X, -1*X, np.identity(X.shape[0]), -1*np.identity(X.shape[0])])
    c = np.vstack([np.zeros((2*X.shape[1], 1)), t*np.ones((X.shape[0], 1)), (1-t)*np.ones((X.shape[0], 1))]).T
    # 線形計画問題を解く
    res = linprog(c, A_eq = A, b_eq = b)
    # 回帰係数計算
    theta_plus = res.x[0:X.shape[1]].reshape(-1, 1)
    theta_minus = res.x[X.shape[1]:2*X.shape[1]].reshape(-1, 1)
    theta = theta_plus - theta_minus
    # 回帰係数保存
    temp_data = pd.DataFrame(theta.T, columns = ['theta0', 'theta1'])
    temp_data['tau'] = t
    coefficients = pd.concat([coefficients, temp_data])

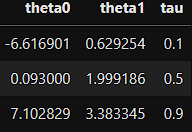
scikit-learnで実行したのと同じ回帰係数が得られています。

Lasso回帰

scikit-learnのQuantileRegressorには「alpha」という引数があり、以下のマニュアルに記載の通り$L1$正則化を行うLasso回帰を行うことができます。

$L1$正則化を取り入れた分位点回帰も正則化なしの場合と同様に線形計画問題として解くことが可能です。Lasso回帰で最小化したい関数は正則化パラメータ$\lambda$を用いて以下のようになります。

\sum_{i=1}^{N}L_{\tau}(y_i-\boldsymbol{x}_i^T\boldsymbol{\theta})+\lambda\sum_{k=1}^{p}|\theta_k|\hspace{10pt}\cdot\cdot\cdot\hspace{10pt}(4)

$(4)$式の第$1$項は通常の分位点回帰と同じです。第$2$項は

\lambda\sum_{k=1}^{p}|\theta_k|=\lambda\sum_{k=1}^{p}(\theta_k^{+}+{\theta_{k}}^{-})=\lambda\boldsymbol{1}_N^T{\boldsymbol{\theta}}^++\lambda\boldsymbol{1}_N^T{\boldsymbol{\theta}}^-

と書くことができるので$(4)$式は

\tau\boldsymbol{1}_N^T\boldsymbol{u}+(1-\tau)\boldsymbol{1}_N^T\boldsymbol{v}+\lambda\boldsymbol{1}_N^T{\boldsymbol{\theta}}^++\lambda\boldsymbol{1}_N^T{\boldsymbol{\theta}}^-

のように変形することができます。したがって、線形計画問題としては

\boldsymbol{c}=\begin{pmatrix}
\lambda\boldsymbol{1}_N  \\
\lambda\boldsymbol{1}_N\\
\tau\boldsymbol{1}_N\\
(1-\tau)\boldsymbol{1}_N
\end{pmatrix}

のようなベクトル$\boldsymbol{c}$を用いて

\newcommand{\min}{\mathop{\rm min}\limits}
\min_{\boldsymbol{z}}\hspace{2pt}\boldsymbol{c}^T\boldsymbol{z}\hspace{5pt}subject\hspace{2pt}to\hspace{5pt}A\boldsymbol{z}=\boldsymbol{b},\hspace{2pt}\boldsymbol{z}\geq\boldsymbol{0}

のように表現すれば良いことが分かります。以下のようにパラメータ推定を行うとscikit-learnのQuantileRegressorでLasso回帰を行ったのと同じ結果が得られます。scikit-learnでは引数に与えた正則化パラメータにサンプルサイズを掛け算した値を実際の正則化パラメータとして使う実装になっているので以下のプログラムはそれに合わせています。

python

# データ準備
X = data[['X0', 'X1']].values
y = data['Y'].values

# 正則化パラメータ
alpha = 0.2

# 分位点回帰実行、回帰係数保存
coefficients = pd.DataFrame()
taus = [0.1, 0.5, 0.9]
for t in taus:
    # 線形計画問題の行列を作成
    b = y.reshape(-1, 1)
    A = np.hstack([X, -1*X, np.identity(X.shape[0]), -1*np.identity(X.shape[0])])
    c = np.vstack([(alpha*y.shape[0])*np.ones((2*X.shape[1], 1)), t*np.ones((X.shape[0], 1)), (1-t)*np.ones((X.shape[0], 1))]).T
    # 線形計画問題を解く
    res = linprog(c, A_eq = A, b_eq = b)
    # 回帰係数計算
    theta_plus = res.x[0:X.shape[1]].reshape(-1, 1)
    theta_minus = res.x[X.shape[1]:2*X.shape[1]].reshape(-1, 1)
    theta = theta_plus - theta_minus
    # 回帰係数保存
    temp_data = pd.DataFrame(theta.T, columns = ['theta0', 'theta1'])
    temp_data['tau'] = t
    coefficients = pd.concat([coefficients, temp_data])

ニューラルネットワークを用いた分位点非線形回帰

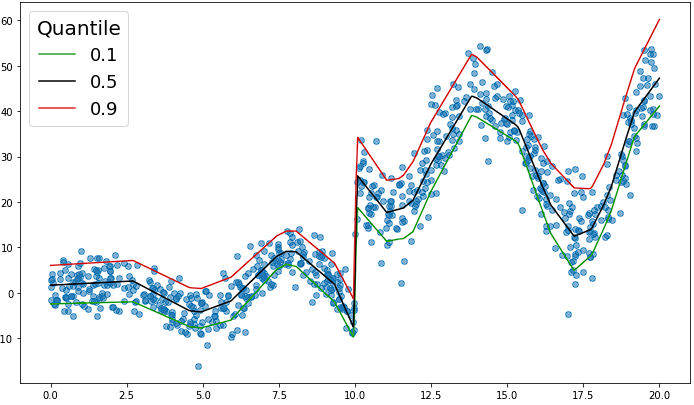
ニューラルネットワークを用いた非線形の分位点回帰を行います。以下のような非線形で不連続な箇所があるようなデータを用います。

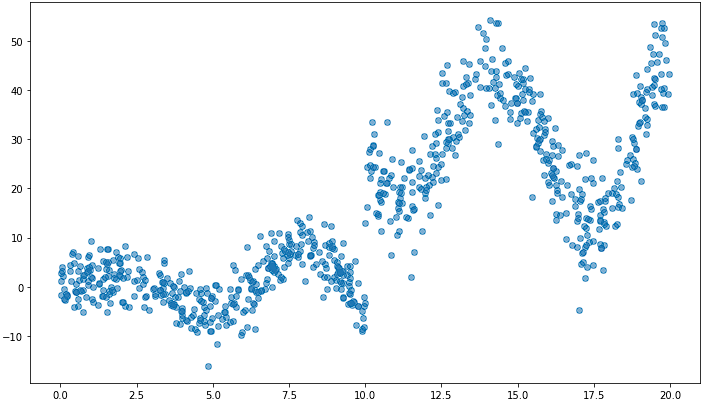
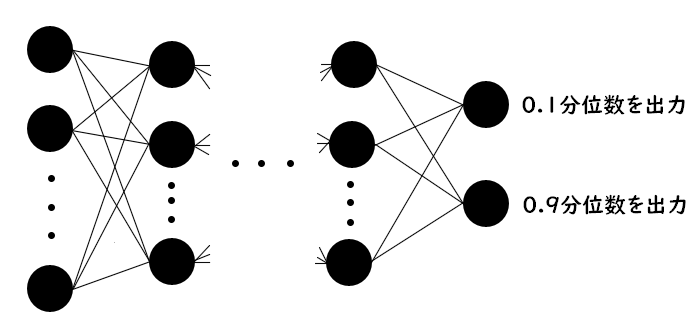
ニューラルネットワークにおいてもこれまでと同様に$(2)$式を最小化するようなパラメータの推定を行います。したがって、$(2)$式を損失関数として学習を行えばニューラルネットワークを用いた分位点回帰を行うことができます。ただし、今回は以下の例ように出力層のユニット数を推定したい分位点の数にすることで1つのニューラルネットワークで複数の分位点を出力できるようにしたいので少し損失関数を変更する必要があります。

出力したい分位数を$\tau_1, \ldots,\tau_s$、出力層に$s$個のユニットを持つニューラルネットワークを$g$とします。このニューラルネットワーク$g$の出力層の$j$番目のユニットと出力したい分位数$\tau_j$を対応付けます。$i$番目のサンプル$\boldsymbol{x}_i$を入力したときのニューラルネットワーク$g$の$j$番目のユニットの出力値を$g_j(\boldsymbol{x}_i)$、ミニバッチのサイズを$n$としたとき、以下の損失関数を最小化するようにニューラルネットワークの学習を行います。

\frac{1}{n}\sum_{j=1}^{s}\sum_{i=1}^{n} L_{\tau_j}(y_i-g_{j}(\boldsymbol{x}_i))

これにより出力層の$j$番目のユニットに$\tau_j$分位数が出力されるようなニューラルネットワークを得ることができます。例として$0.1, 0.5, 0.9$分位数を出力するようなニューラルネットワークの学習を行って、回帰曲線をプロットすると以下のようになります。まあまあ上手くいってそうです。

おわりに

範囲をもって予測したり、ばらつき量の変動を捉えたりするのに使うといい感じかなぁ。

参考文献

■記事内の分析に用いたプログラム

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up