More than 5 years have passed since last update.

数値計算Advent Calendar 2018

FreeFem++の紹介

Last updated at 2018-12-20Posted at 2018-12-19

この記事は数値計算 Advent Calendar 2018 の20日目の記事です.
昨日は @nqomorita さんによる「有限要素法と反復法線形ソルバのはじめの一歩」でした.
明日は @adhara_mathphys さんがご担当です.

2日連続で有限要素法に関する話題です.

FreeFem++とは?

FeeeFem++ (旧ページ) とは, 偏微分方程式に対する有限要素法のためのプログラミング言語およびソフトウェアで, パリ第6大学のJ. L. Lions研究所によって開発・保守されています.
読み方は「ふりーえふいーえむ (ぷらすぷらす)」だと思います¹.
FreeFem++では, 2次元・3次元の様々な偏微分方程式を比較的簡単に取り扱うことができます.
C++言語をベースに書かれているため, プログラミング経験があれば比較的容易に入門できると思います.

有限要素法を自分でプログラミングしようとすると,

三角形分割
(多次元の) 数値積分
線形ソルバ

など, 面倒なアルゴリズムを自分で記述する必要があり, 非専門家には非常にハードルが高くなりますが, FreeFem++を用いれば, これらをすべてソフトウェアにお任せすることができます.
また, 有限要素法の数学的な記述を, ほぼそのままの形で書くことでプログラミングができる, という大きなメリットもあります.
したがって, 数学の専門家にもオススメできます.

本稿では, (Windows環境での) FreeFem++の基本的な使い方と, 解の可視化方法を紹介します.
本稿の読者としては, ある程度のプログラミング経験がある人を想定しています.

有限要素法の詳細な解説は割愛しましたが, 末尾に付録として簡単な (数学的) 解説を付けました.
付録部分は, 大学の学部1・2年生レベルの数学をある程度身に付けている人であれば, 読み進められるのではないかと思います.
また, 昨日の「有限要素法と反復法線形ソルバのはじめの一歩」では, 有限要素法の物理的な解説がなされていますので, 併せてご参照ください.

お詫び

書きたいことを書き並べた結果, とても長くなりました. すみません.

FreeFem++に興味があるけどあまり良く知らない, という方は, まずは, この節と使い方と実装の部分だけを読んで, それ以降は後回しにしても良いと思います².
その後, 可視化の方法に興味を持った場合や, そもそもFreeFem++の可視化機能に不満がある方は, 可視化の節をお読みください.

利用方法

FreeFem++は, 以下のいずれかの形式で利用できます.

コマンドラインで利用: FreeFem++
統合開発環境で利用: FreeFem++-cs
オンライン (JavaScript) で利用: FreeFem++-js

オンラインで利用できるJS版は, 「試しにちょっと使ってみたい!」という方におすすめです.

通常のFreeFem++は, 本家サイトからDLできます.
EmacsやAtomなどのエディタにはシンタックスハイライトも用意されています (詳細).

FreeFem++-csはここでDLできますが, Windows版を利用する場合は通常のFreeFem++もDLしておく必要があります.
DLページのUbuntu版などに含まれるFreeFem++のバージョンを見る限り, FreeFem++-csがちゃんと保守されているのかわからないのですが, 簡単に使う分には困らないので, 以下では, FreeFem++-cs の使い方を紹介します³.

ドキュメント

公式ドキュメント: 最近できたばかりのようで, TODOとなっている箇所が多いですが, チュートリアルはちゃんと書かれているようです.
PDF版マニュアル: 情報が豊富なので, 困ったらこれを読んでいます.

日本語で書かれた資料としては,

明治大学の桂田先生による「FreeFem++の紹介」および「FreeFem++ノート」
東京大学の齊藤先生による「FreeFem++による楕円型方程式の数値計算」
大塚厚二, 高石武史. 「有限要素法で学ぶ現象と数理 ―FreeFem++数理思考プログラミング―」, 共立出版, 2014 とそのサポートサイト

が参考になります. 特に, 桂田先生によるpdfファイルは, 本稿の内容の大部分を含んでいます.

FreeFem++-csの使い方

まずは, ダウンロード&インストール方法と, 簡単な操作方法を説明します.

ダウンロード

DLページで自分の環境にあったものをDLしてください.
Windowsの場合は, FreeFem++ DLページでFreeFem++本体もDLしておく必要があります.

インストール

DLしたファイルをダブルクリックし, Next等をクリックして最後にInstallをクリックでOKです.
FreeFem++本体をWindowsにインストールする場合は Add application directory to your system path にチェックを入れておくと良いです.

操作方法

FreeFem++-csを起動すると, 以下のようなウィンドウが開きます:

上側の左半分はエディタ
上側の右半分は可視化用の領域
下側は出力用の領域

です. エディタの部分にコードを記述し, 左上のボタンまたはショートカットキーで保存や実行などの操作をします.

左上の3つのボタンは, 以下のような働きをします.

ボタン	働き	ショートカットキー (Windows)
	保存	`Ctrl + S`
	実行	`Ctrl + Shift + R`
	停止	無し?

FreeFEM++での実装

FreeFem++-csでのコードの書き方を簡単に解説します.
(有限要素法に関しては付録を参照)

ここでは例として, 正方形領域 $\Omega = (0,1)^2$ 上のPoisson方程式⁴

\begin{cases}
-u_{xx}(x,y) - u_{yy}(x,y) = f(x,y) , & (x,y) \in \Omega, \\
u(x,y) = 0, & (x,y) \in \Gamma
\end{cases}

を考えます⁵. $\Gamma = \partial\Omega$ は $\Omega$ の境界です.

有限要素法では, 領域 $\Omega$ を三角形分割するのでした.
その三角形の集合を $\mathcal T_h$ とおきます. $h$ は三角形の最大辺長です.
さらに, $\mathcal T_h$ に付随する区分的1次多項式の空間を

V_h = \{ v_h \in C^0(\overline{\Omega}) \mid \text{任意の $K \in \mathcal T_h $ に対し, $v_h|_K$ は1次多項式} \}

とおき, $V_h$の中で斉次境界条件を満たす関数全体の空間を

V_{h,0} = \{ v_h \in V_h \mid v_h|_\Gamma = 0 \}

とします.
このとき, Poisson方程式に対する有限要素法は, 弱形式

\iint_\Omega (u_{h,x} v_{h,x} + u_{h,y} v_{h,y}) \, dxdy = \iint_\Omega fv_h \, dxdy, \quad \forall v_h \in V_{h,0}

を満たす関数 $u_h \in V_h$ を見つける問題, となります.
この式の中の関数 $v_h$ をテスト関数と呼ぶのでした.

ひとまず, 外力 $f$ は, $f(x,y) = 5 \pi^2 \sin(\pi x) \sin(2 \pi y)$ とします.
このとき, 厳密解は $u(x,y) = \sin(\pi x) \sin(2 \pi y)$ です.

まずは実装例

細かい説明は後回しにして, まずはFreeFem++-csで近似解が計算される様子を見ます.

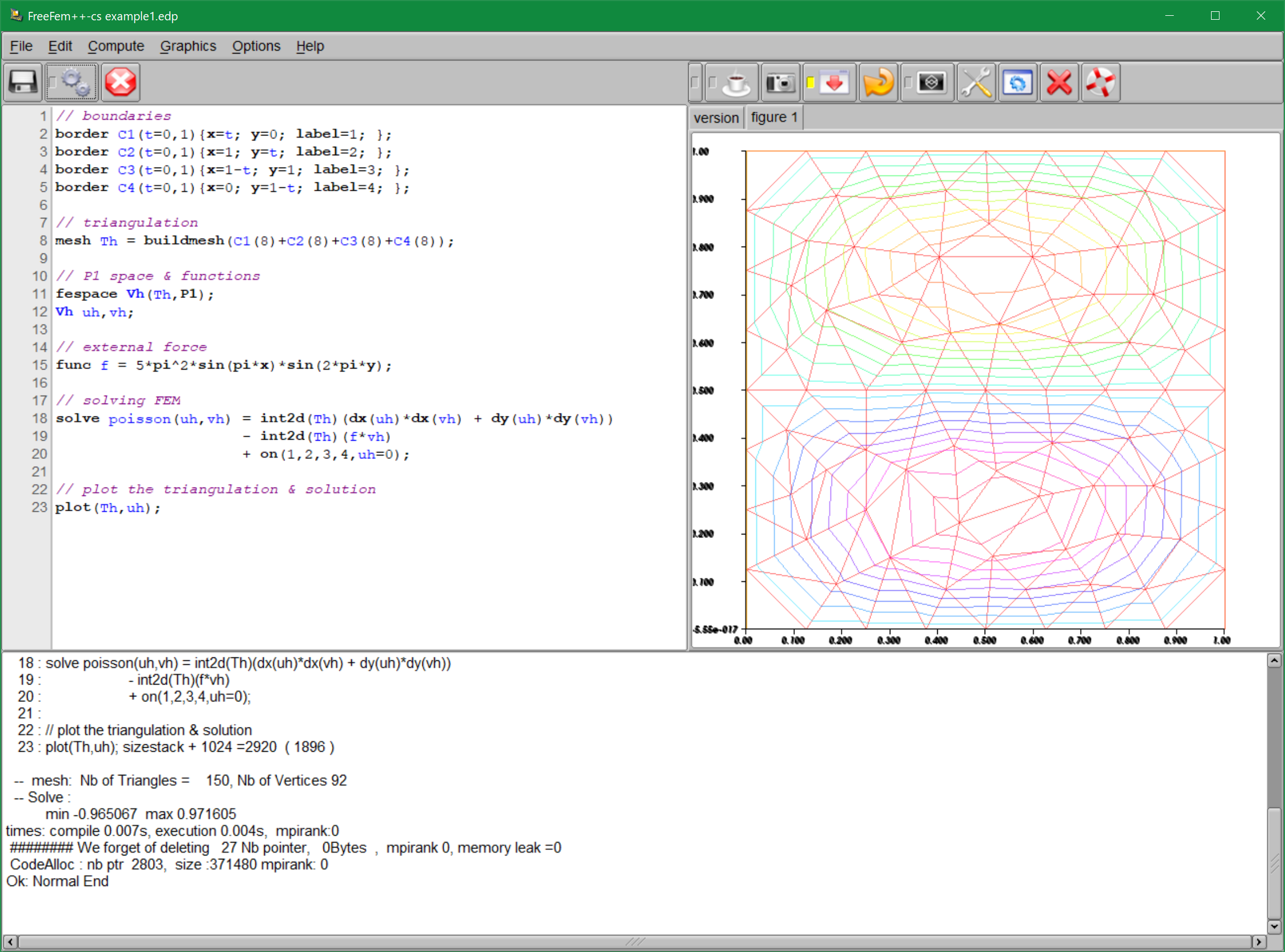
上述の問題に対する有限要素法をFreeFem++-csで実装するためには, FreeFem++-csのエディタ部分に, 以下のように記述をします.
ファイルを保存しなくても実行できますが, ここでは example1.edp という名前で保存することにします.
FreeFem++では, .edp という拡張子が推奨されているようです⁶.

example1.edp

// boundaries
border C1(t=0,1){x=t; y=0; label=1; };
border C2(t=0,1){x=1; y=t; label=2; };
border C3(t=0,1){x=1-t; y=1; label=3; };
border C4(t=0,1){x=0; y=1-t; label=4; };

// triangulation
mesh Th = buildmesh(C1(8)+C2(8)+C3(8)+C4(8));

// P1 space & functions
fespace Vh(Th,P1);
Vh uh,vh;

// external force
func f = 5*pi^2*sin(pi*x)*sin(2*pi*y);

// solving FEM
solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh)) 
                     - int2d(Th)(f*vh) 
                     + on(1,2,3,4,uh=0);

// plot the triangulation & solution
plot(Th,uh);

ファイルを保存した後, 実行ボタン (歯車のボタン, または Ctrl + Shift + R) で実行すると, FreeFem++-csのウィンドウは以下のようになります:

下側の出力エリアにいろいろと書かれていますが, とにかく Ok であることがわかります.
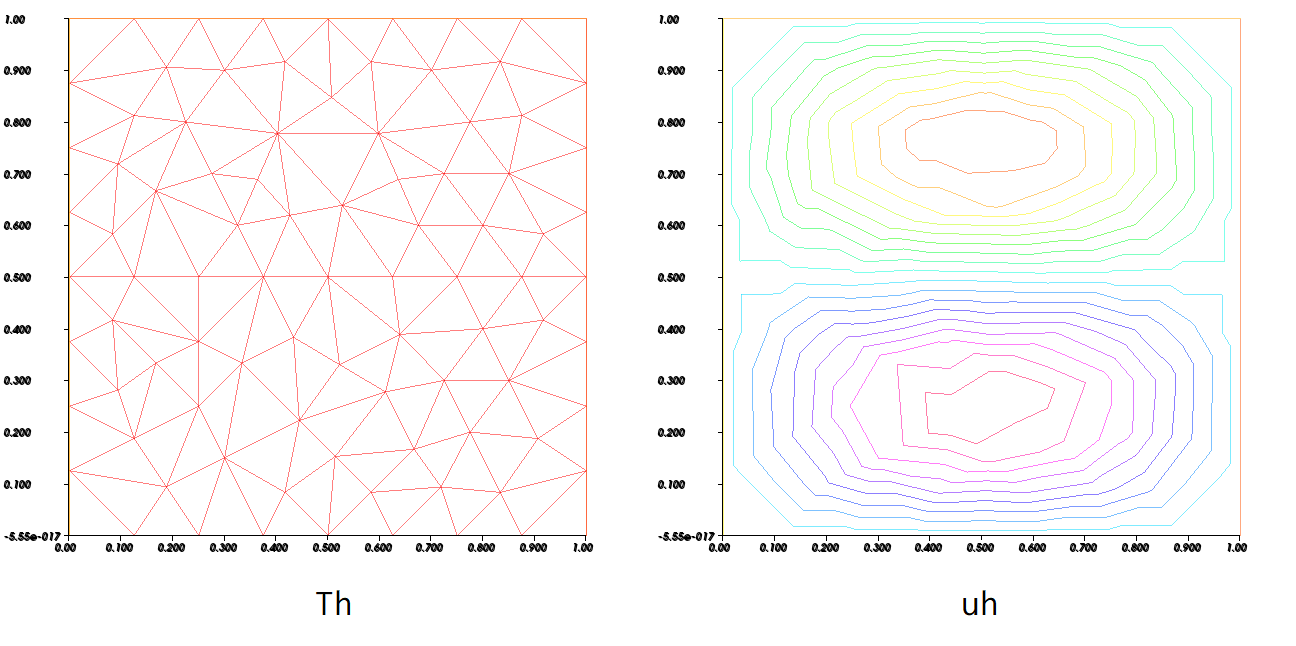
右側の可視化エリアには, 三角形分割と近似解の等高線が描画されていますが, (特に等高線の) 見栄えはあまりよろしくありません.

以下では, 各命令の意味を解説します.
また, 次節で可視化の調整方法について説明します.

各命令の解説

全般

まずは, 全体に関わる事項を説明します.

行末

まず, C++ベースで書かれているということもあり, 基本的には行末にセミコロンを書きます.
セミコロンを書かずに改行すると, 同じ行として扱われます (多分).

コメントアウト

何度か現れる // で始まる行はコメント行です.
コメントの書き方もC言語と同様です.
つまり, /* ... */ という書き方も可能です. こちらの書き方なら複数行のコメントアウトも可能です.

数式

他の言語と基本的には同じと思って差し支えないと思います.
例えば四則演算は + - * / ですし, べき乗は ^ です.
C言語のように, 整数型同士で割り算をすると, 整数型になります. 例えば 1/2 は 0 になります.
円周率は pi です.

変数

上の例では現れていませんが, C言語のように変数を定義することができます.
整数は int, 浮動小数点数は real⁷, 複素数は complex で記述します.
配列も定義できます. インデックスは0からです.

例えば以下のような記述が可能です.

int n=8, m=10, nn;
int[int] M;
M[0] = -1; M[1] = m;

real a=1.0, b;
real[int] A;
A[0] = -2.0; A[1] = a;

領域の記述

example1.edp

// boundaries
border C1(t=0,1){x=t; y=0; label=1; };
border C2(t=0,1){x=1; y=t; label=2; };
border C3(t=0,1){x=1-t; y=1; label=3; };
border C4(t=0,1){x=0; y=1-t; label=4; };

この4行で正方形の各辺 (つまり, 領域の境界) を記述しています.
よく読むと分かると思いますが, 各辺の曲線としてのパラメータ表示をほぼそのまま記述しています.
実際, C1 ～ C4 はそれぞれ,

\begin{cases} x=t, \\ y=0, \end{cases} \qquad
\begin{cases} x=1, \\ y=t, \end{cases} \qquad
\begin{cases} x=1-t, \\ y=1, \end{cases} \qquad
\begin{cases} x=0, \\ y=1-t \end{cases}

という曲線 (直線) たちを表しています (すべて $0 \le t \le 1$).
パラメータ表示されている曲線であれば何でも取り扱えるので, 正方形に限らず, 様々な形状の領域を取り扱うことが可能です.
具体的な書き方は,

border 曲線の名前(パラメータ){x=パラメータ表示; y=パラメータ表示; label=曲線の番号};

です.

「曲線の名前」は割と何でも良いです.
「パラメータ」の部分は, t=0,1, theta=0,2*pi などのように, 名前=上限,下限 という形で書きます.
「パラメータ表示」の部分は, 実際のパラメータ表示を書きます.
- ただし, 反時計回りが正の向きとなるようにします.
- 正方形の下の辺は, パラメータ $t \in [0,1]$ を用いて $x=t, , y=0$ と書かれるので, そのように記述します.
「曲線の番号」の部分は, 境界条件の設定の際に使います. ここには整数を記述します.
- 異なる曲線に同じ番号を割り振ることも可能です.

正方形ではなく単位円周を用いる場合は, 次のようになります. 3つとも同じ境界になります.

// いずれも同じ境界
border circle1(t=0,2*pi){x=cos(t); y=sin(t); label=1; };
border circle2(s=-pi,pi){x=cos(t); y=sin(t); label=1; };
border circle3(theta=0,1){
    x=cos(2*pi*theta); 
    y=sin(2*pi*theta); 
    label=1; 
};

最後の例のように, 内部で改行しても大丈夫です.

三角形分割

example1.edp

// triangulation
mesh Th = buildmesh(C1(8)+C2(8)+C3(8)+C4(8));

この行で三角形分割をしています.
書き方は,

mesh 分割の名前 = buildmesh(境界の名前(分割数)+...)

です.

「分割の名前」は割と何でも良いです.
buildmesh コマンドが分割のためのコマンドです.
- 中身の「境界の名前」の部分は, 先程の border の部分で定義した名前 (今の場合 C1 ～ C4) を用います.
- 今の例の場合, 以下のような操作を意味します.
  1. 曲線 C1 のパラメータ区間 ($=[0,1]$) を7 (=8-1) 等分することで曲線を7等分し, 得られる8個の点を順に結ぶ.
  2. 他の曲線 C2 ～ C4 に対しても同様の操作を行う
  3. C1 → C2 → C3 → C4 の順につなぐ
- C1(8) が手順1.に対応していて, + でつなぐことが手順3.に対応しています.
- ただし, 境界をつなぐ順番は何でも良いわけではなく, 連続的につながるようにします.
  - 例えば, buildmesh(C2(8)+C3(8)+C4(8)+C1(8)) はOKですが, buildmesh(C1(8)+C3(8)+C2(8)+C4(8)) はダメです.
- 「分割数」の部分は整数値を記入します. 数が大きいほど細かな分割になります. 曲線ごとに異なる数字を記入しても大丈夫です.
  - また, 負の値を記述することもできます. その場合は, 曲線の向きが逆になります⁸.

注目すべき点は, 境界の分割数だけを与えれば良いという点です. これだけで, 内部の分割は自動でやってくれます.
しかも, いい感じの三角形分割⁹を生成してくれます.

引数には変数が入っても問題ないので, 以下のような記述も可能です.

int n=16;
mesh Th = buildmesh(C1(n)+C2(n)+C3(n)+C4(n));

有限要素空間

example1.edp

// P1 space & functions
fespace Vh(Th,P1);
Vh uh,vh;

fespace Vh(Th,P1); の部分で区分的1次多項式の空間 $V_h$ を定義しています.
書き方は,

fespace 空間の名前(分割の名前,P1);

です.

「空間の名前」は割と何でも良いです.
「分割の名前」は, 先述の mesh で定義した名前 (今の場合は Th) を記述します.
P1 で「区分的1次多項式を用いますよ」という意味になります.
- 境界条件は付与されないので, 上の $V_{h,0}$ は定義されません.
- この部分には, 決められた文字列しか記述できません.
- P1 の他には, P0, P2, P1dc などが利用可能です. それぞれ, 「区分的多項式」「区分的2次多項式」「三角形間で不連続な区分的1次多項式」の意味です.

その後の Vh uh,vh; の部分は, Vh の元 uh, vh を, 変数のように生成しています.

ちなみに, 後述の func で定義される関数を用いて,

Vh fh = f;

と書くと, f をLagrange補間¹⁰した関数が定義されます.

関数

example1.edp

// external force
func f = 5*pi^2*sin(pi*x)*sin(2*pi*y);

この行では関数を定義しています.
書き方は,

func 関数の名前 = 定義式;

です.
この例では, x と y が現れますが¹¹, これらは予約語です. そのまんま, $x$ 座標と $y$ 座標の意味です.
関数の定義も, ほぼそのまま記述できるというのは便利なポイントの1つです.

また, 特性関数も簡単に記述できます. 例えば, 単位円板の特性関数

\chi(x,y) = \begin{cases} 1, & x^2 + y^2 < 1 \\ 0, & x^2+y^2 \ge 1 \end{cases}

なら,

func chi = x^2+y^2<1;

と記述できます. また,

func chi = (x^2+y^2<1)*sin(x)*cos(y);

といった記述も可能です.
条件式の部分は true か false を返すわけですが, 数式の中では true=1, false=0 として扱われることを利用しています.

弱形式の記述

example1.edp

// solving FEM
solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh)) 
                     - int2d(Th)(f*vh) 
                     + on(1,2,3,4,uh=0);

ここがFreeFem++のミソです. たった3行 (改行しなければ1行) で, 連立一次方程式の係数行列と右辺ベクトルを作成し, 適切なソルバで解くということをやってくれます.
しかも, この部分も, 弱形式の表記をほぼそのまま記述できているという点が大きな特徴です.

書き方は,

solve 問題の名前(近似空間の元,近似空間の元) = 弱形式 + on(境界の番号,Dirichlet境界条件);

となっています. ただし,

「問題の名前」は割と何でも良いです¹².
「近似空間の元」を2つ書きますが, 1つ目が近似解, 2つ目がテスト関数を意味します. 今の場合は uh が近似解になります.
「弱形式」の部分で積分を記述します.
- FreeFem++では, 弱形式の右辺をすべて左辺へ移項して, $... = 0$ の形にしたときの右辺を記述します.
- int2d は2次元の重積分を行う, というコマンドです. 下でもう少し説明します.
+on(...) の部分でDirichlet境界条件¹³を記述します.
- 「境界の番号」は, 境界を定義した border ... の部分の label=... で定めた番号を記述します.
- Dirichlet境界条件を課したい境界だけ番号を記述します. 例えば, 下側にDirichlet条件を課さないなら, +on(2,3,4,uh=0) となります¹⁴.
- +on(1,2,3,4,uh=f) などと書けば, 非斉次境界条件も取り扱えます.

弱形式は積分で書かれていますが, (二重)積分は int2d という簡便なコマンドで記述することが可能です.

書き方は, int2d(分割名)(被積分関数) です.
「分割名」は, mesh の部分で定義した変数 (今の場合は Th) を記入します.
被積分関数の中の dx(uh) は, $x$ での偏微分を意味します. つまり, dx(uh) $ = \frac{\partial}{\partial x}$uh です.
同様に dy は $y$ での偏微分です.

積分も, 数学的な記述をほぼそのまま利用できるという点が重要です.
また, Neumann境界条件を扱うときは境界での積分が必要ですが, その場合は int1d というコマンドを利用します.
利用例は付録1を参照してください.

細かな注意点として, 弱形式の「左辺」(未知関数を含む項) と「右辺」(含まない項) は分けて書かなければならない, という点が挙げられます.
例えば,

solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh) - f*vh) 
                     + on(1,2,3,4,uh=0);

と書いてしまうと, エラーになってしまいます.

解の可視化

example1.edp

// plot the triangulation & solution
plot(Th,uh);

plotで三角形分割や解を可視化します. 三角形分割と関数を別々に可視化することも可能です.

plot(Th); // triangulation
plot(uh); // solution

三角形分割はともかく, 解の可視化はあまり良いとは言えません.
次節ではこの点についてもう詳しく少し取り扱います.

解をより見やすく可視化する

FreeFem++-csでの可視化の調整

FreeFem++-csでの plot コマンドにオプションをつけることで, 多少見た目を改善することができます.
以下では, 近似解 uh のみを可視化することにします.

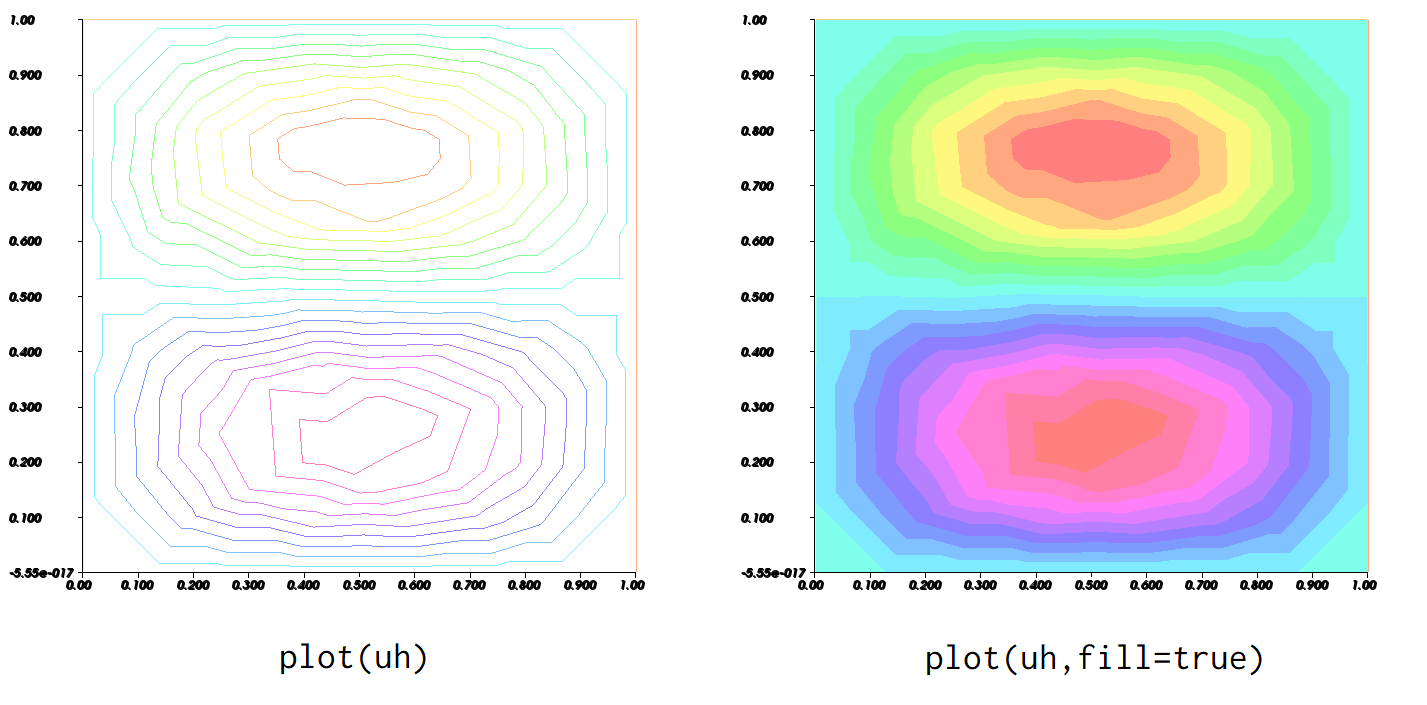
色を塗りつぶす

fill=true を追加すると, 多少見た目が改善されます.

plot(uh,fill=true);

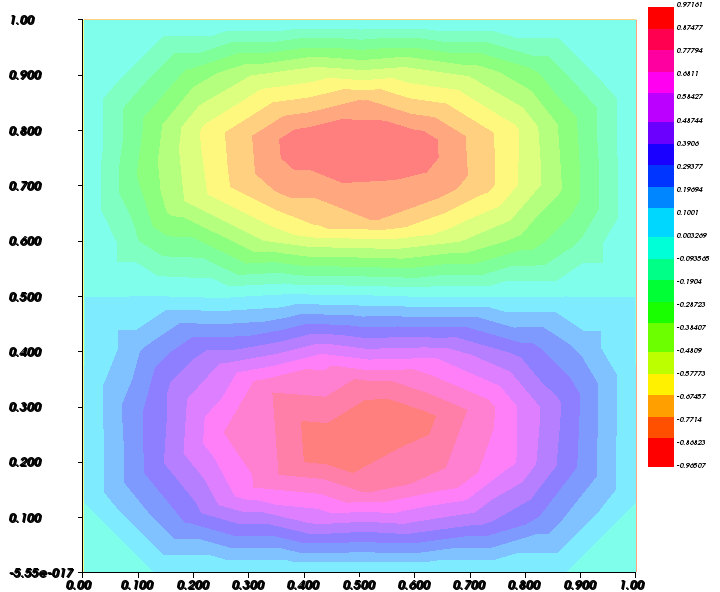
結果:

カラーバーを表示する

value=true を追加すると, カラーバーを表示しますが, 位置をいじることはできなさそうです.

plot(uh,fill=true,value=true);

結果:

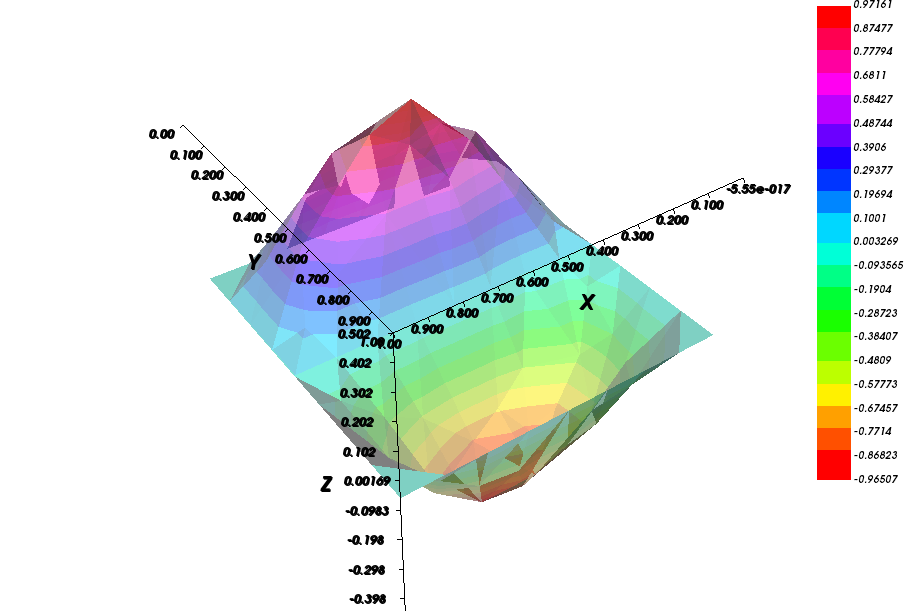
グラフとして表示する

dim=3 を追加すると, グラフとして表示されます.

plot(uh,fill=true,value=true,dim=3);

結果:

画像として保存する

これは見た目の調整ではありませんが, ps="ファイル名.png" を追加すると, 指定したファイル名で画像を保存します.
対応している拡張子は, 少なくとも png と eps ですが, pdf には対応していません.

カラースキームを変える

デフォルトだと, 一番大きな値と一番小さな値が同じ色で表示されてしまいますが, これはわかりにくいと思います.
しかし, 他の可視化ソフトのようにカラースキームが用意されているわけではないようなので, 手動で色の範囲等を変える必要があります.
これは非常に面倒ですから, 正直オススメできません.

論文に載せる図のように, 細かく見た目を調整する場合は, 以下のように他のソフトウェアを利用することをオススメします.

gnuplot, Matlab, Octaveによる可視化

FreeFem++では, 三角形分割や解のデータを外部ファイルに出力することができます.
そのファイルを他の可視化ソフトで読み込むことで, 可視化させることができます.

つまり,

FreeFem++-csで計算
計算結果を csv ファイルなどで出力
外部の可視化ツールで読み込み, 可視化

という手順を踏めば良いということです.
具体例として, gnuplotを利用する方法と, MatlabまたはOctaveを利用する方法が公式ドキュメントに記載されているので, 紹介だけします.
なお, この節の内容はあまり詳しく書きません. 詳細は上のドキュメントを参照してください.

gnuplotによる可視化

おそらく世界で一番有名な可視化ソフト gnuplot で可視化する方法は, 多くのドキュメントで紹介されています.
しかし, gnuplot自体が三角形分割に対応していないので, 以下のように線で可視化することしかできないし, 線の前後関係もおかしくなります.
手軽に可視化できるので, このようなデメリットが気にならない人にはオススメです.

gnuplotによる可視化の例:

雰囲気は良さそうですが, よく見ると, 中央付近の線が重なっているところで線の前後関係がわかりにくくなっています.

Matlab, Octaveによる可視化

これは私自身が試したことがないのでわかりませんが, 結構きれいに可視化できるようです.
詳しくはwebドキュメントを参照してください¹⁵.

その他, meditやParaviewなどを利用する方法もあるようですが, ここでは割愛します.

matplotlibによる解の可視化

「データとして出力 → 外部ソフトで可視化」という手順であれば, 上に挙げたソフトウェアでなくても可視化はできるはずです.
そこでここでは, pythonの可視化ライブラリである**matplotlib**による可視化を紹介したいと思います.
この方法のメリットとしては,

gnuplotと同程度 (or それ以上) の機能を用いることができ, 見た目を編集する際の自由度が高い
三角形分割の可視化に対応しているので, 面による可視化が可能

といった点が挙げられます.

python & matplotlibのダウンロードとインストール

複数の方法がありますが, 個人的にはAnacondaを経由してインストールをするのが楽で良いと思います.

FreeFem++でのデータの出力

FreeFem++-cs に以下のように記述して, example2.edp というファイル名で保存します.

example2.edp

// boundaries
border C1(t=0,1){x=t; y=0; label=1; };
border C2(t=0,1){x=1; y=t; label=2; };
border C3(t=0,1){x=1-t; y=1; label=3; };
border C4(t=0,1){x=0; y=1-t; label=4; };

// triangulation
mesh Th = buildmesh(C1(8)+C2(8)+C3(8)+C4(8));

// P1 space & functions
fespace Vh(Th,P1);
Vh uh,vh;

// external force
func f = 5*pi^2*sin(pi*x)*sin(2*pi*y);

// solving FEM
solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh)) 
                     - int2d(Th)(f*vh) 
                     + on(1,2,3,4,uh=0);

// output

ofstream tri("Th.csv");
for(int i=0;i<Th.nt;i++){
	tri << Th[i][0] << "," << Th[i][1] << "," << Th[i][2] << endl;
}

ofstream sol("uh.csv");
for(int i=0;i<Th.nv;i++){
	sol << Th(i).x << "," << Th(i).y << "," << uh[][i] << endl;
}

solve コマンドまでは example1.edp と同じですが, 最後の方が異なっています.
この部分で, データの出力をしています¹⁶.

`ofstream` コマンド

まず, ofstream で出力ファイルを指定します.

ofstream 変数名("ファイル名");

という書き方をします.
ファイル名の拡張子は csv でも txt でも dat でも, テキストファイルならば何でもOKです.
変数名は, 出力時に用いる変数です.

出力は

変数名 << 出力する値や文字列 << ... << endl;

とします.
<< でそれに続く値や文字列を「変数名」に対応するファイルに順に出力します.
endl は改行を出力することを意味します.
例えば, 上の例で

sol << 1.0 << 2.0 << ",    " << 3 << endl;

と書くと, sol に対応するファイル uh.csv には,

uh.csv

1.02.0,    3

と書かれます.

細かい補足 [クリックで開く]

`ofstream` は指定されたファイルを開くのですが, 上のコードにはファイルを閉じるコマンドがありません. ファイルを閉じる必要がある場合は, 中括弧を用いてブロックを作ります. 具体的には, 以下のようにします.

{
    ofstream tri("Th.csv");
    for(int i=0;i<Th.nt;i++){
        tri << Th[i][0] << "," << Th[i][1] << "," << Th[i][2] << endl;
    }
}

このようにすることで, 最後の } でファイルが閉じられ, tri という変数も無くなります.

また, 外部ファイルではなく, ウィンドウ下部の出力エリアに表示させる場合は, cout を用います.
例えば,

cout << f(0.0,0.0) << endl;

などのようにすれば, 下のエリアに $f(0,0)$ の値が出力されます.
ちょっとした確認に便利です.

三角形分割の情報, 解の情報

for 文の中に Th.nt などの値がありますが, これらは三角形分割の情報を与えます.
具体的には, 以下のような情報を取り出せます (三角形分割の変数名を Th とします).

値	意味
`Th.nv`	頂点の個数
`Th.nt`	三角形の個数
`Th(i).x`	`i` 番目の頂点の $x$ 座標
`Th(i).y`	`i` 番目の頂点の $y$ 座標
`Th[j][k]`	`j` 番目の三角形の `k` 番目の頂点の番号

インデックスはどれも0から始まるので, 上の表では

インデックス	下限	上限
`i`	$0$	`Th.nv`${}-1$
`j`	$0$	`Th.nt`${}-1$
`k`	$0$	$2$

となっています.

また, 近似解からも情報を取り出すことができます.

値	意味
`uh[][i]`	`i` 番目の頂点における `uh` の値

となっています. この場合のインデックスも0から始まるので, 表中の i の上限は Th.nv${}-1$ です¹⁷.

他にも Th や uh から取り出せる情報はありますし, 有限要素空間 Vh からも情報を取り出すことができますが, ここでは割愛します.
詳細は, pdf版のマニュアル (か, 上に挙げた本) を参照してください.

for文

C言語と同じように書けばOKです. つまり,

for(イテレータの初期値;終了条件;更新方法){
    ...
}

です.

データの構造

三角形分割

まずは, 1個目の出力部分

ofstream tri("Th.csv");
for(int i=0;i<Th.nt;i++){
	tri << Th[i][0] << "," << Th[i][1] << "," << Th[i][2] << endl;
}

を見てみましょう.
この部分では, 三角形分割の情報を出力し, Th.csv というファイルに保存しています.

上で説明したように, 「Th[j][k] は j 番目の三角形の k 番目の頂点番号」なので, 整数値を返します.
したがって, この出力では, 「第 i 行目に, i番目の三角形の頂点番号を順に並べたcsvファイル」を生成することになります.
実際, Th.csv の最初の数行は以下のようになっています.

Th.csv

0,1,2
4,1,3
13,4,10
5,1,4
4,3,10
...

近似解

次に, 2個目の出力部分

ofstream sol("uh.csv");
for(int i=0;i<Th.nv;i++){
	sol << Th(i).x << "," << Th(i).y << "," << uh[][i] << endl;
}

を見ましょう.
この部分では, 三角形分割の頂点の座標と, 対応する座標での解の値を出力し, uh.csv というファイルに保存しています.
この場合は, 「第 i 行目に, i 番目の頂点の座標と, そこでの解の値を順に並べたcsvファイル」を生成します.
uh.csv の最初の数行は, 以下のようになっています.

uh.csv

0,1,-2.81623e-061
0,0.875,-2.52905e-031
0.125,1,-3.10341e-031
0,0.75,-3.66729e-031
0.125,0.8125,-0.336199
...

matplotlibでの読み込み

以上のようにして出力したファイル Th.csv と uh.csv を, matplotlibで読み込みましょう.
matplotlibはpythonのライブラリなので, 以下のようにpythonのスクリプトファイルを作ります.
お好きなテキストエディタに以下を記入し, 例えば trisurf.py という名前で保存します.
内容は後で軽く説明します.

trisurf.py

# import packages
import matplotlib.pyplot as plt
import matplotlib.tri as mtri
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd

# read data
coord = pd.read_csv('uh.csv',header=None).values
x = coord[:,0]
y = coord[:,1]
z = coord[:,2]
tridata = pd.read_csv('Th.csv',header=None).values
tri = mtri.Triangulation(x,y,triangles=tridata)

# plot
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_trisurf(tri,z,cmap=plt.cm.jet)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('u')
plt.show()

そして, コマンドプロンプトやPowerShell等で

python trisurf.py

と入力すると, 以下のようなウィンドウが現れます.

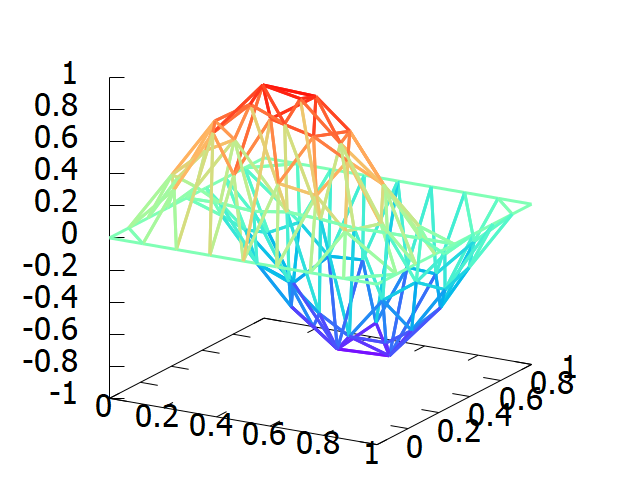
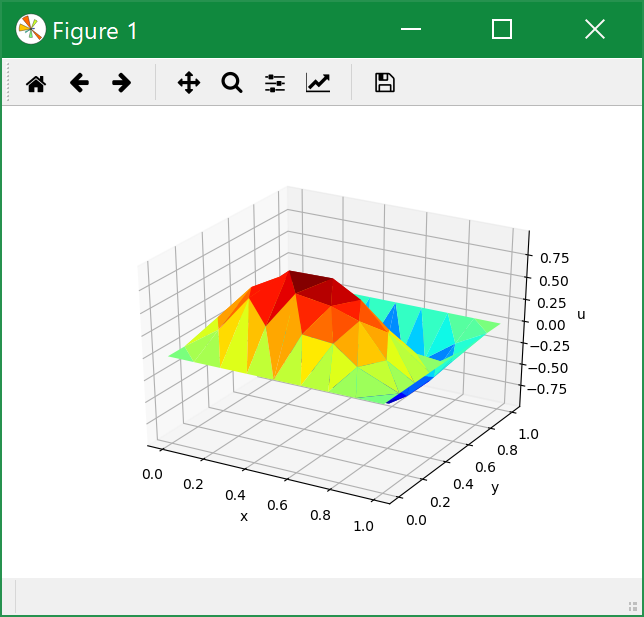
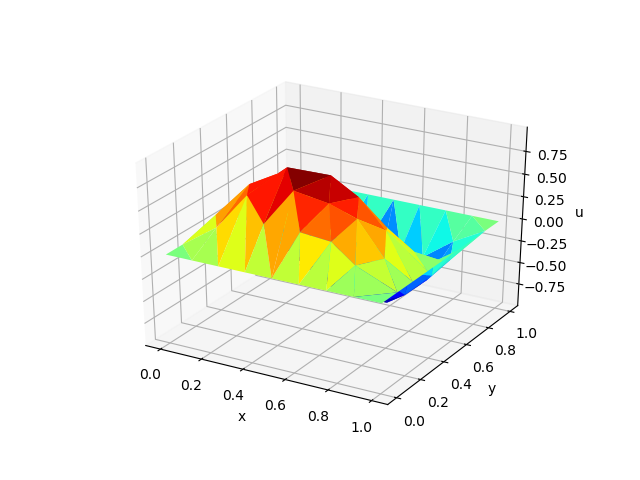
FreeFem++-csやgnuplotのときと比べて, 遥かに綺麗な図ができた思います.
グラフをマウスでグリグリと回すことができるので, 好きな角度のところで右上のフロッピーディスクのボタンを押すと, 画像として保存することができます.

また, 最後の plt.show() を plt.savefig('filename.png') とすることでも, 画像ファイルを保存することが可能です.
実際に保存された画像は次のようになります.

コードの内容

先程の trisurf.py の中身を簡単に説明します.

まず, 冒頭の

trisurf.py

# import packages
import matplotlib.pyplot as plt
import matplotlib.tri as mtri
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd

の部分では, 必要なパッケージをインポートしています.

最初の3つは三角形分割の可視化のために必要です.
4個目は csv ファイルの読み込みのために必要です.

その後の

trisurf.py

# read data
coord = pd.read_csv('uh.csv',header=None).values
x = coord[:,0]
y = coord[:,1]
z = coord[:,2]
tridata = pd.read_csv('Th.csv',header=None).values
tri = mtri.Triangulation(x,y,triangles=tridata)

の部分で, データを読み込んでいます.

pd.read_csv('uh.csv',header=None) の部分で uh.csv 読み込んでいます.
- header=None というオプションは, 今の場合は必須です.
- ただ, これだけだとデータフレームという型になってしまい, matplotlibでは取り扱えないので, .values を追記して配列に直します.
その後の x = coord[:,0] などで, $x$ 座標だけの配列, を作っています. この配列 x は, 「第 i 成分が i番目の頂点の $x$ となっている配列」です.
更に, tridata = pd.read_csv('Th.csv',header=None).values で csv ファイルを読み込み, その後の tri = mtri.Triangulation(x,y,triangles=tridata) で, 三角形分割のデータを作っています.

最後の

trisurf.py

# plot
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_trisurf(tri,z,cmap=plt.cm.jet)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('u')
plt.show()

の部分が可視化の部分です.

最初の2行 fig = plt.figure() と ax = fig.gca(projection='3d') で, 描画領域の設定をしています.
ax.plot_trisurf(tri,z,cmap=plt.cm.jet) の部分が重要で, ここでグラフを可視化しています.
- cmap=plt.cm.jet はカラーマップを指定しているだけなので, 無くても良いですが, matplotlibではカラーマップがたくさん用意されている (詳細) ので, 好きなように色を変えることができます.
- plot_trisurf の詳細はここやここを参照してください.
ax.set_xlabel('x') などは軸ラベルを設定しているだけなので, 無くても良いです.
最後の plt.show() で, グラフを表示しています.

matplotlibには, 様々な機能があるため, グラフ以外の部分 (軸など) もかなり自由に見た目を変えることができます.
詳細なドキュメントはいたるところにあるので, 興味のある方は調べてみてください.

終わりに

説明が長くなってしまいましたが, 本稿でお伝えしたいことは

FreeFem++を用いれば, 比較的簡単に, 様々な領域上の偏微分方程式が解ける
可視化は, matplotlibなど, 自分が使い慣れたツールを利用すると, キレイな図を作れる

ということです.
本稿ではPoisson方程式しか説明しませんでしたが, 熱方程式, 波動方程式, Schrodinger方程式, Stokes方程式などの各種線形方程式から, Navier-Stokes方程式などの非線形方程式まで, 多くの偏微分方程式を取り扱うことができます.
また, matplotlibを利用した可視化を解説しているドキュメントは, (日本語では) 本稿しか存在しないと思います.

もし興味を持ってくださった方がいましたら, 最初に述べたオンライン版のFreeFem++-jsで, 上の example1.edp を走らせてみてください¹⁸.

また, よくわからない偏微分方程式の解を計算して様子を観察することで, 研究にも役立てることが可能かもしれません.
多くの方がFreeFem++を通じて偏微分方程式や有限要素法へ参入してくれることを願っています.

付録1: ギャラリー

ここでは, 比較的大事だけど本文で説明しきれなかったこと, を紹介しますが, ソースコードや出力結果だけを紹介するにとどめます.

以下, ギャラリー [クリックで開く]

領域

円板領域

freefem

border C(t=0,2*pi){x=cos(t); y=sin(t); label=1;};
mesh Th=buildmesh(C(32));

穴の空いた領域

freefem

border C1(t=0,2*pi){x=cos(t); y=sin(t); label=1;};
border C2(t=0,2*pi){x=0.5*cos(t)+0.1; y=0.4*sin(t)+0.2; label=2;};
mesh Th=buildmesh(C1(32)+C2(-16));

バウムクーヘン型領域

border arc1(t=0,pi/2.0){x=cos(t); y=sin(t); label=1;};
border line1(t=0,0.5){x=0; y=1-t; label=2;};
border arc2(t=0,pi/2.0){x=0.5*cos(0.5*pi-t); y=0.5*sin(0.5*pi-t); label=3;};
border line2(t=0.5,1){x=t; y=0; label=4;};
mesh Th=buildmesh(arc1(16)+line1(8)+arc2(8)+line2(8));

種々の境界値問題

Neumann 境界条件問題¹⁹

\begin{cases}
-u_{xx} - u_{yy} + u = f, & \text{in } \Omega, \\
\partial_n u = g, & \text{in } \Gamma. 
\end{cases}

ただし, $\partial_n$ は境界 $\Gamma$ における外向き法線微分.
弱形式は,

\iint_\Omega (u_x v_x + u_y v_y + uv ) \, dxdy = \iint_\Omega fv \, dxdy + \int_\Gamma gv ds,
\quad \forall v \in V.

ただし, $\int_\Gamma \cdot ds$ は $\Gamma$ 上の線積分であり,

V = \{ v \in L^2(\Omega) \mid v_x, v_y \in L^2(\Omega) \} \quad [\, =H^1(\Omega) \,]

である.

freefem

// boundaries
border C1(t=0,1){x=t; y=0; label=1; };
border C2(t=0,1){x=1; y=t; label=2; };
border C3(t=0,1){x=1-t; y=1; label=3; };
border C4(t=0,1){x=0; y=1-t; label=4; };

// triangulation
mesh Th = buildmesh(C1(8)+C2(8)+C3(8)+C4(8));

// P1 space & functions
fespace Vh(Th,P1);
Vh uh,vh;

// external forces
func f = x+y;
func g = sin(pi*x)*cos(pi*y);

// solving FEM
solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh) + uh*vh) 
                     - int2d(Th)(f*vh) 
                     - int1d(Th,1,2,3,4)(g*vh);

Robin 境界条件問題²⁰

\begin{cases}
-u_{xx} - u_{yy} = f, & \text{in } \Omega, \\
\partial_n u ＋\alpha u = g, & \text{in } \Gamma.
\end{cases}

ただし, $\alpha$ は $\Gamma$ 上で与えられた正値の関数.
弱形式は,

\iint_\Omega (u_x v_x + u_y v_y) \, dxdy + \int_\Gamma \alpha uv \, ds = \iint_\Omega fv \, dxdy + \int_\Gamma gv ds,
\quad \forall v \in V.

ただし,

V = \{ v \in L^2(\Omega) \mid v_x, v_y \in L^2(\Omega) \}

である.

freefem

// boundaries
border C1(t=0,1){x=t; y=0; label=1; };
border C2(t=0,1){x=1; y=t; label=2; };
border C3(t=0,1){x=1-t; y=1; label=3; };
border C4(t=0,1){x=0; y=1-t; label=4; };

// triangulation
mesh Th = buildmesh(C1(8)+C2(8)+C3(8)+C4(8));

// P1 space & functions
fespace Vh(Th,P1);
Vh uh,vh;

// external forces
func f = x+y;
func g = sin(pi*x)*cos(pi*y);
func a = 1.0;

// solving FEM
solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh))
                     + int1d(Th,1,2,3,4)(a*uh*vh) 
                     - int2d(Th)(f*vh) 
                     - int1d(Th,1,2,3,4)(g*vh);

混合境界値問題 (その1)

\begin{cases}
-u_{xx} - u_{yy} + u = f, & \text{in } \Omega,
u ＝ g, & \text{on } \Gamma_1,
\partial_n u = h, & \text{in } \Gamma_2.
\end{cases}

ただし, $\Gamma_1, \Gamma_2 \subset \Gamma$, $\Gamma_1 \cup \Gamma_2 = \Gamma$. $\Gamma \cap \Gamma_2 = \emptyset$ である.
弱形式は,

\iint_\Omega (u_x v_x + u_y v_y) \, dxdy = \iint_\Omega fv \, dxdy + \int_{\Gamma_2} gv ds,
\quad \forall v \in V.

ただし,

V = \{ v \in L^2(\Omega) \mid v_x \in L^2(\Omega), \, v|_{\Gamma_1} = 0 \}

である.

freefem

// boundaries
border C1(t=0,1){x=t; y=0; label=1; };
border C2(t=0,1){x=1; y=t; label=2; };
border C3(t=0,1){x=1-t; y=1; label=3; };
border C4(t=0,1){x=0; y=1-t; label=4; };
border C5(t=0,2*pi){x=0.4+0.3*cos(t); y=0.3+0.2*sin(t); label=5;};

// triangulation
mesh Th = buildmesh(C1(8)+C2(8)+C3(8)+C4(8)+C5(-16));

// P1 space & functions
fespace Vh(Th,P1);
Vh uh,vh;

// external force
func f = x+y;
func g = sin(pi*x)*cos(pi*y);
func h = x*y;

// solving FEM
solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh))
                     - int2d(Th)(f*vh) 
                     - int1d(Th,5)(h*vh)
                     + on(1,2,3,4,uh=g);

混合境界値問題 (その2)

freefem

// boundaries
border C1(t=0,1){x=t; y=0; label=1; };
border C2(t=0,1){x=1; y=t; label=2; };
border C3(t=0,1){x=1-t; y=1; label=1; };
border C4(t=0,1){x=0; y=1-t; label=2; };

// triangulation
mesh Th = buildmesh(C1(8)+C2(8)+C3(8)+C4(8));

// P1 space & functions
fespace Vh(Th,P1);
Vh uh,vh;

// external force
func f = x+y;
func g = sin(pi*x)*cos(pi*y);
func h = x*y;

// solving FEM
solve poisson(uh,vh) = int2d(Th)(dx(uh)*dx(vh) + dy(uh)*dy(vh))
                     - int2d(Th)(f*vh) 
                     - int1d(Th,2)(h*vh)
                     + on(1,uh=g);

三角形分割だけを可視化 (gnuplotを利用)

まず, FreeFem++-csで以下を実行.

freefem

border C1(t=0,2*pi){x=cos(t); y=sin(t); label=1;};
mesh Th=buildmesh(C1(16));

ofstream tri("mesh.plt");
for(int i=0;i<Th.nt;i++){
    for(int j=0;j<3;j++){
        tri << Th[i][j].x << " " << Th[i][j].y << endl ;
    }
    tri << Th[i][0].x << " " << Th[i][0].y << endl << endl;
}

次に, 好きなテキストエディタで以下のファイルを作成²¹.

mesh.bat

set term pngcairo
set output "mesh.png"
set size square
unset key
unset tics
unset border
plot "mesh.plt" w l 
set term wxt

最後に, コマンドプロンプトやPowerShellで以下を実行.

gnuplot mesh.bat

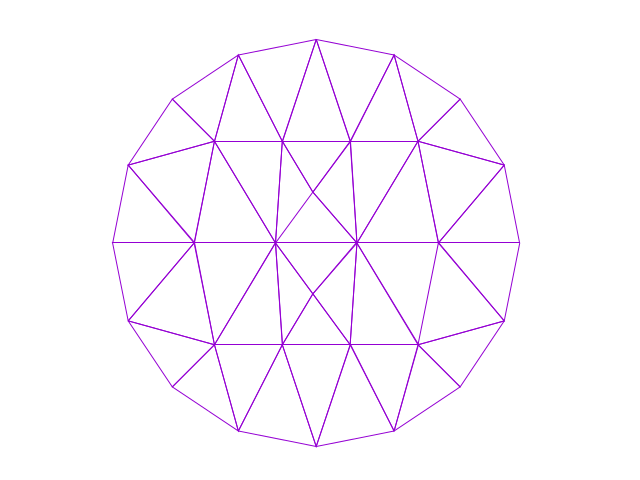
以下の画像 mesh.png が得られる.

上の青線の三角形分割も, この方法で可視化して, 分割数や線を調整したものです.
具体的には, plot の部分で

plot "mesh.plt" w l lw 2 lc "web-blue"

としています.

付録2: 有限要素法超概説

ここでは有限要素法を非常に雑に説明します.
詳しいことは, 適切な文献を参照してください.

有限要素法の解説: 長いので注意 [クリックで開く]

Poisson方程式と弱形式

$\Omega \subset \mathbb{R}^2$ を有界領域とし, $\Omega$ 上のPoisson方程式

\begin{cases}
-u_{xx}(x,y) - u_{yy}(x,y) = f(x,y) , & (x,y) \in \Omega, \\
u(x,y) = 0, & (x,y) \in \Gamma
\end{cases}
\tag{P}

を考えます.
ここで, $f$ は与えられた関数であり, $\Gamma := \partial\Omega$ は $\Omega$ の境界です.

突然ですが, 次の関数空間 (関数の集合²²) を考えます:

V := \{ v \in L^2(\Omega) \mid v_x, v_y \in L^2(\Omega) ,\ v|_\Gamma = 0 \}.

ここで, $L^2(\Omega) = \{ v \colon \Omega \to \mathbb{R} \mid \iint_\Omega |v(x,y)|^2 , dxdy < \infty \} $ は2乗可積分な関数全体の集合です.
実は, この空間 $V$ はSobolev空間²³ という空間の一種であり, 普通は $H^1_0(\Omega)$ と書かれます.
Sobolev空間の詳細は割愛しますが, 本稿では, 「1階まで微分ができて, 自分自身と1階偏導関数が全て2乗可積分である」という性質を満たすもの全体, と捉えておけば十分です.

さて, 方程式(P)の両辺に, 任意の $v \in V$ をかけて, $\Omega$上で積分します²⁴:

-\iint_\Omega (u_{xx} + u_{yy}) v \, dxdy = \iint_\Omega f v \, dxdy.

左辺にGreenの公式を適用します. ここで, Greenの公式とは, スカラー値関数 $f$ とベクトル値関数 $\mathbf{g}$ に対して,

\iint_\Omega f \operatorname{div} \mathbf{g} \, dxdy
= \iint_\Gamma f \mathbf{g} \cdot n \, ds - \iint_\Omega \nabla f \cdot \mathbf{g} \, dxdy

が成り立つ²⁵ ($n$ は $\Gamma$ の外向き単位法線ベクトル, $ds$ は $\Gamma$ 上の線積分), という公式でした.

-\iint_\Omega (u_{xx} + u_{yy}) v \, dxdy = \iint_\Omega \nabla u \cdot \nabla v \, dxdy

となります.
したがって, 今までの計算から, 問題(P)の解 $u$ は, 次を満たすことがわかります:

\iint_\Omega (u_x v_x + u_y v_y) \, dxdy = \iint_\Omega fv \, dxdy, \quad \forall v \in V.
\tag{W}

この式(W)を, 問題(P)の弱形式と呼びます²⁶.

ここまでは問題(P)から初めて式(W)まで来ましたが, 逆に, 問題(P)を忘れて, 式(W)から始めてみましょう.
実は, Lax-Milgramの定理²⁷と呼ばれる関数解析の理論を用いることで, 次の定理が示せます.

$\Omega \subset \mathbb{R}^2$ を領域とする.
このとき, 任意の $f \in L^2(\Omega)$ に対して, (W)を満たす関数 $u$ が, $V$ の中に一意的に存在する.

この定理によって得られる $u \in V$ を, 問題(P)の弱解と呼びます²⁸.

領域 $\Omega$ が適切な条件²⁹を満たしているならば, 弱解 $u$ は2階微分可能³⁰で, 問題(P)の解³¹となっている.

という定理が知られています.
したがって, 問題(P)の代わりに弱形式(W)を考えても, ある意味で問題ない, ということになります.

実は, 有限要素法は, 弱形式に基づいて弱解を近似する離散化手法です.

Galerkin法³²と (P1)有限要素法

Galerkin法

空間 $V$ は無限次元の関数空間なので, コンピュータで扱うことができません.
しかし, 有限次元の関数空間であれば, コンピュータで扱うことができます.
そこで, $N$ 次元の部分空間 $V_N \subset V$ を考えて, 次の方程式を満たす $u_N \in V_N$ を探すことを考えます:

\iint_\Omega (u_{N,x} v_{N,x} + u_{N,y} v_{N,y}) \, dxdy = \iint_\Omega fv_N \, dxdy, \quad \forall v_N \in V_N.
\tag{W$_N$}

このときも, 先述のLax-Milgramの定理により,

任意の $f \in L^2(\Omega)$ に対して, ($\mathrm{W}_N$) を満たす関数 $u_N$ が, $V_N$ の中に一意的に存在する.

ということがわかります.
有限次元の空間で得られる解 $u_N \in V_N$ と実際の解 $u \in V$ は当然別物ですが, 空間の次元 $N$ を無限大にすることで $u_N \to u$ となると期待しているわけです.
このようにして弱解を近似する手法を, Galerkin法と呼びます.

方程式($\mathrm W_N $)が, 連立1次方程式に帰着されることを示します.
$V_N$ の基底を $\phi_i$ ($i=1,2,\sots,N$) とします.
このとき, 近似解は $u_N = \sum_{j=1}^N u_j \phi_j$ と書けるので, 近似解 $u_N$ を求めることは, 係数 $u_j$ を求めることに他なりません.
この表記を ($\mathrm{W}_N$) に代入し, $v_N = \phi_i$ を代入すると, 以下を得ます.

\sum_{j=1}^N u_j \iint_\Omega (\phi_{j,x} \phi_{i,x} + \phi_{j,y} \phi_{i,y}) \,dxdy = \iint_\Omega f \phi_i \, dxdy,
\quad \forall i

そこで, $a_{ij} = \iint_\Omega (\phi_{j,x} \phi_{i,x} + \phi_{j,y} \phi_{i,y}) ,dxdy$, $f_i = \iint_\Omega f \phi_i , dxdy$ とおくと,

\sum_{j=1}^N a_{ij} u_j = f_i,
\quad \forall i

と書けます.
これは連立1次方程式を表しています.

このときの係数行列を $A := (a_{ij})_{i,j} \in \mathbb{R}^{N \times N}$ とおきます.
係数行列 $A$ は, 定義から対称行列であることがすぐに分かりますが, それだけでなく, 正定値行列です.
実際, 任意のベクトル $v=(v_i) \in \mathbb{R}^N$ に対し, 少し計算すると,

v^T A v = \iint_\Omega | nabla v_N |^2 \, dxdy \ge 0,
\quad v_N := \sum_{j=1}^N v_j \phi_j \in V_N

となり, $A$ は半生定値であることがわかります.
しかも, この $v_N$ は境界条件 $v_N|_\Gamma = 0$ を満たすので,

v^T A v = 0 \iff \nabla v_N \equiv 0 \iff v_N \equiv 0

がわかります³³.
したがって, 係数行列 $A$ は正定値対称行列となり, SOR法などが適用可能であるとわかります.

なお, 有限次元に落とすことで, コンピュータで扱えるようになるだけでなく, 数学的にも取り扱いが楽になるので, Galerkin法は偏微分方程式の理論分野でも広く用いられています.

有限要素法

有限次元空間 $V_N$ の決め方は様々ですが, ここでは区分的1次多項式で生成される空間を考えます.

領域 $\Omega$ は多角形であると仮定します.
このとき, 領域 $\Omega$ を, 小さな三角形に分割します.

このときの三角形の集合を $\mathcal{T}$ と書き, 領域の内部にある頂点の個数を $N$ とするとき,

V_N = \{ u_N \in C^0(\overline{\Omega}) \mid \text{任意の $K \in \mathcal{T}$ に対し, $u_N|_K$ は1次多項式 }, \, u_N|_\Gamma = 0 \}

とおきます. 言葉で書くと,

領域全体で連続で, 各三角形の上で1次多項式となり, 境界では0となる関数全体の集合

が, 今の $V_N$ です.
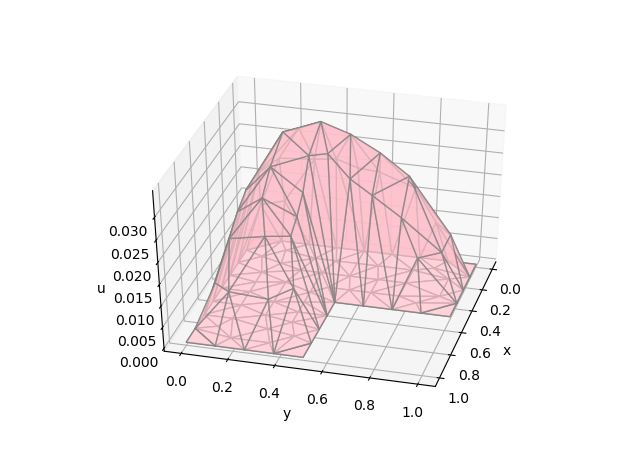
例えば, 以下の図のような関数が $V_N$ に属します.

折れ線の2次元版に対応するものなので, 「折れ面」と表現することもできます.
関数が折れているところでは微分ができませんが, 三角形ごとに微分したものを導関数と思えば, $V_h \subset V$ であると言えます.

このような関数空間でGalerkin法を実行する手法を, P1有限要素法 (あるいは, 単に有限要素法) と呼びます.
P1は, 1次多項式の意味です³⁴.
Galerkin法の方程式 ($\mathrm W_N $) は連立1次方程式に帰着され, 係数行列が正定値対称となると述べましたが, 有限要素法の場合, その係数行列が疎行列となる (ような基底関数を選べる³⁵) ことが知られています.
したがって, 共役勾配法などの, 疎行列向けのソルバを利用することが可能です.

有限要素法の界隈では, 次元に対応するパラメータとして, 頂点の個数ではなく, 三角形の最大辺長を用います.
実際, 頂点の個数を多くするだけでは, 折れ面で関数を近似できるとは限りません³⁶が, 最大辺長を小さくすれば, 近似できそうであると期待が持てます³⁷.

三角形の最大辺長は $h$ と書かれることが多く, 最大辺長が $h$ であるような三角形の集合を $\mathcal T_h$, 対応する関数空間を $V_h$, 対応する近似解を $u_h$ と書きます. つまり,

V_h = \{ u_h \in C^0(\overline{\Omega}) \mid \text{任意の $K \in \mathcal T_h $ に対し, $u_h|_K$ は1次多項式 }, \, u_h|_\Gamma = 0 \}

有限要素法に関しては, 以下の誤差評価が知られています.

$u$ をPoisson方程式(P)の解, $u_h$ を有限要素法による近似解とする.
このとき, 三角形分割 $\mathcal T_h$ が適切な条件を満たすならば,
 \| \nabla (u-u_h) \|_{L^2(\Omega)} \le C h 
が成り立つ.
さらに, 多角形領域 $\Omega$ が凸ならば,
$$ \| u-u_h \|_{L^2(\Omega)} \le C h^2 $$
が成り立つ.
ただし, $C$ は $h$ には依存しない定数である.

三角形分割の「適切な条件」とは, 直感的に言うと, 「三角形が潰れない」という条件です.

この誤差評価から, 「良い三角形分割を構成できれば, 有限要素法によって良い近似解が得られる」ということがわかりました.

有限要素法をコンピュータで実装するには,

領域の三角形分割 (「適切な条件」を満たすように)
連立1次方程式の係数行列と右辺ベクトルの作成 (そのためには数値積分が必要)
連立1次方程式のソルバ

が必要です. 3点目に関しては多くの言語でライブラリを活用できるのであまり気にならないかもしれませんが, 上2つはなかなか面倒です.
しかし, FreeFEM++を用いれば, これらをソフトウェアに丸投げすることができるのです.

FEM = Finite Element Method = 有限要素法 ↩
これだけでも十分に長くなってしまったのですが... ↩
Windows環境での利用を想定. MacだとFreeFem++-csは動いたり動かなかったりする模様? ↩
ポアソン. ↩
普通は, 第1式左辺を, Laplacianを用いて $-\Delta u$ と書きますが, FreeFem++での記述と合わせるために, あえてこのように書きます. ↩
edp = équations aux dérivées partielles (仏) = partial differential equations であるとこの講義ノートにかかれているが, 出典は不明. ↩
double ではない. ↩
領域に穴を開ける時に使います. ↩
Delaunay (ドロネー) 三角形分割という分割を生成してくれます. ↩
ラグランジュ. $f_h \in V_h$ が $f$ のLagrange補間である $\iff$ 三角形分割の各頂点 $P$ において, $f_h(P) = f(P)$. ↩
すでに境界の定義の部分で現れていますが... ↩
問題に名前をつけて何の意味があるのか? と思うかもしれませんが, 熱方程式を解くときのように, 反復処理を行う際に必要になります. その際は solve ではなく problem というコマンドを用います. ↩
ディリクレ, ディリシュレ. ↩
この場合, 下側の境界には斉次Neumann (ノイマン) 境界条件 $\frac{\partial u}{\partial \nu} = 0$ が課された問題を近似していることになります. ↩
なぜかpdf版マニュアルには記載されていません. ↩
C++と同じ記法を用います. ↩
この部分は区分的1次多項式の場合のみ正しい情報です. わかっている人向けの説明: uh[][i] は「空間 Vh の i 番目の節点における uh の値」を返します. 例えばP2要素の場合は, 「Vh の i 番目の節点」=「Th の i 番目の頂点」とは限らないために, uh[][i] の意味が表に書いた通りではなくなります. もし, P1要素以外の場合で可視化のためのデータ出力をしたいのであれば, 「i 番目の頂点における uh の値」は uh(Th(i).x,Th(i).y) と記述する必要があります. これは, uh(x0,y0) で「点 (x0,y0) における uh の値」を意味することを利用しています. ↩
コピペをして Run をクリックするだけです.
様々な形の (2次元) 領域上の偏微分方程式の解を可視化できると, それだけで少し楽しい気持ちになります. ↩
ノイマン. ↩
ロバン ↩
文字コードの関係で, メモ帳は避けたほうが良い可能性? ↩
線形空間として見ているときは「空間」と呼びます. ↩
ソボレフ. ↩
以下, 独立変数 $x$, $y$ は, 混乱の恐れがない限りは省略します. ↩
念のため: $\operatorname{div} \mathbf{g} = g_{1,x} + g_{2,y} , , \nabla f = ( f_x, f_y )^T $.
Greenの公式において, $f=v$, $\mathbf{g} = \nabla u$ とおくと, $v|_\Gamma \equiv 0$ により, ↩
左辺には1階微分までしか現れておらず, 2階微分が現れていないことに注意. ↩
ラックス, ミルグラム. ↩
$V$ の元は1階微分可能性までしか保証されないことに注意
さらに, ↩
例えば, 「有界領域で, 境界が $C^2$ 級」, 「有界凸多角形領域である」など. ↩
$H^2(\Omega)$ に属するという意味. ↩
$L^2$ 関数として $-\Delta u = f$ を満たす, という意味. ↩
ガレルキン, ガラーキン ↩
$\nabla v_N \equiv 0$ ならば $v_N$ は定数関数となることに注意. ↩
区分的2次多項式や3次多項式を用いることもあります. 一般にはP$k$有限要素法などと呼びます. ↩
ある頂点で1, それ以外の頂点で0, となるような関数を基底関数とすれば良い. ↩
例えば, 正方形領域の半分だけに頂点を増やしても, 残りの半分ではうまく関数を近似できない. ↩
実は一般には正しくない. ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

FreeFem++の紹介

FreeFem++とは?

利用方法

ドキュメント

関連ページ

FreeFem++-csの使い方

ダウンロード

インストール

操作方法

FreeFEM++での実装

まずは実装例

各命令の解説

全般

行末

コメントアウト

数式

変数

領域の記述

三角形分割

有限要素空間

関数

弱形式の記述

解の可視化

解をより見やすく可視化する

FreeFem++-csでの可視化の調整

色を塗りつぶす

カラーバーを表示する

グラフとして表示する

画像として保存する

カラースキームを変える

gnuplot, Matlab, Octaveによる可視化

gnuplotによる可視化

Matlab, Octaveによる可視化

matplotlibによる解の可視化

python & matplotlibのダウンロードとインストール

FreeFem++でのデータの出力

ofstream コマンド

三角形分割の情報, 解の情報

for文

データの構造

三角形分割

近似解

matplotlibでの読み込み

コードの内容

終わりに

付録1: ギャラリー

領域

円板領域

穴の空いた領域

バウムクーヘン型領域

種々の境界値問題

Neumann 境界条件問題19

Robin 境界条件問題20

混合境界値問題 (その1)

混合境界値問題 (その2)

三角形分割だけを可視化 (gnuplotを利用)

付録2: 有限要素法超概説

Poisson方程式と弱形式

Galerkin法32と (P1)有限要素法

Galerkin法

有限要素法

`ofstream` コマンド

Neumann 境界条件問題¹⁹

Robin 境界条件問題²⁰

Galerkin法³²と (P1)有限要素法