まえがき
本資料は、数値計算 Advent Calendar 2018 の 19 日目の記事として作成しました。有限要素法と、有限要素離散化後に得られる連立一次方程式を求解する反復法線形ソルバについて、滑らかに理解するためのものを目指しています。本資料前編の範囲では、熱伝導解析の有限要素離散化を説明します。
はじめに
我々の身の回りに溢れている構造物は、その使用時に様々な力を受けます。この力によって構造物は変形し、時にはその力がある閾値を超えることで、構造物は疲労・破壊に至り、我々の安全を脅かすものとなります。従って、構造物の変形を理解し、安全な設計をすることが重要です。実構造物は膨大な数の複雑な部品で構成されるため、その中で生じる現象を実験的に理解することは、大変難しいものとなります。そこで、構造物の変形などの物理現象を、適切な支配方程式によって理解することを試みます。しかし、これら支配方程式は一般に非線形となり、解析的に解くことは非常に困難です。また、そこで、支配方程式を離散化し数値的に解くことで解を得る方法、すなわち、数値解析がひとつの解決策となります。特に、複雑な任意形状を表現することが容易な点で、有限要素法による数値解析が用いられます。
熱伝導解析における支配方程式
本資料では、有限要素法による熱伝導解析を対象に説明を進めます。フーリエの法則は、式 (1) で表されます。概略図を図 1 に示します。
\phi = - \lambda \nabla \theta \tag{1}
ここで、$\phi$は熱流束 $[{\rm W}/{\rm m}^2]$、$\theta$は温度 $[{\rm K}]$、$\lambda$は熱伝導率 $[{\rm W}/({\rm m} \cdot {\rm K})]$です。
図1：フーリエの法則
熱量保存則は、式 (2) で表されます。
\rho c \dot{\theta} = - \nabla \cdot \phi + f \tag{2}
ここで、$\rho$は密度 $[{\rm kg}/{\rm m}^3]$、$c$は比熱 $[{\rm J}/({\rm kg} \cdot {\rm K})]$、$\dot{\theta} = \partial \theta/\partial t$は温度の時間変化率、$f$は発熱量 $[{\rm W}/{\rm m}^3]$です。
式 (1) を式 (2) に代入すると、支配方程式 (3) が得られます。
\rho c \dot{\theta} = \nabla \cdot (\lambda \nabla \theta) + f \tag{3}
図2：計算領域
次に、図 2 のように、領域$\Omega$を考え、その境界を$\Gamma$とします。あわせて、Neumann境界が定義された境界$\Gamma_{\rm N}$とDirichet境界が定義された境界$\Gamma_{\rm D}$を、式 (4)、式 (5) のように定義します。
\Gamma = \Gamma_{\rm N} \cup \Gamma_{\rm D} \tag{4}
\Gamma_{\rm N} \backslash \Gamma_{\rm D} = \emptyset \tag{5}
このとき、Neumann境界$\Gamma_{\rm N}$において熱流入量$q$が、Dirichet境界$\Gamma_{\rm D}$において温度$\theta$が、それぞれ式 (6)、式 (7) のように定義されるとします。
q = \lambda \nabla \theta \;\; {\rm on} \;\; \Gamma_{\rm N} \tag{6}
\theta = \theta_0 \;\; {\rm on} \;\; \Gamma_{\rm D} \tag{7}
仮想仕事の原理
有限要素法による離散化を行う手始めとして、仮想仕事の原理をおさらいします。物理学における仕事$w$の定義は「質点に加わる力ベクトル$\boldsymbol{f}$と質点の変位ベクトル$\boldsymbol{u}$の内積」によって定義されるスカラー量でした。
w = \boldsymbol{f} \cdot \boldsymbol{u} \tag{8}
次に、図 3 のように、ある質点において力が釣り合っている状態、すなわち加わる力ベクトル$\boldsymbol{f}_i$の和（$1 \lt i \lt n$）が零である状態、式 (9) を考えます。
図3：質点における力の釣り合い
\sum_i^n \boldsymbol{f}_i = 0 \tag{9}
ここで式 (10) のように仮想変位$\delta \boldsymbol{u}$を導入します。仮想変位とは、質点における力の釣り合いを変化させないような無限小の変位のことです。
\delta \boldsymbol{u} = (\delta u_x, \delta u_y, \delta u_z) \tag{10}
仕事の定義式 (8) から、力が加わっている物体が変位すると、その内積の分だけ仕事がなされることがわかっていました。そこで、仮想変位によってなされる仕事$\delta w$を考えます。この仕事のことを、仮想仕事と呼びます。
\delta w = \boldsymbol{f}_1 \cdot \delta \boldsymbol{u} + \boldsymbol{f}_2 \cdot \delta \boldsymbol{u} + \ldots \\
= \sum_i^n \boldsymbol{f}_i \cdot \delta \boldsymbol{u} \tag{11}
このとき、式 (11) では式 (9) に示す質点における力の釣り合いが保たれているため、仮想変位によってなされる仕事は零であることがわかります。
\delta w = 0 \tag{12}
以上までのお気持ちを簡潔にまとめると、「仮想変位によってなされる仕事が零であれば、力ベクトルは釣り合っている」ということが、仮想仕事の原理です。ここまでは質点系に対して考察を進めましたが、式 (11) を質点から連続体の領域に置き換えたものが、式 (13) で表されます。
\delta w = \sum_i^n \int_{\Omega} \boldsymbol{f}_i (\Omega) \cdot \delta \boldsymbol{u}(\Omega) \; {\rm d} \Omega = 0 \tag{13}
例えば、連続体力学における仮想仕事式も、式 (13) と同様の形式になっていることがわかります。次項で説明する有限要素法による熱伝導解析も、このアナロジーによって仮想的温度の適用を考えます。
仮想的温度の適用
ここまでに得られた、支配方程式 (3) について、有限要素離散化を考えます。式 (3) に左から仮想温度$\delta \theta$を乗じ、領域$\Omega$で積分すると、式 (14) を得ます。仮想温度は聞き慣れない言葉ですが、ここでは Virtual Temperature Principle の対訳として使用しました。
\int_{\Omega} \delta \theta \; \rho c \; \dot{\theta} \; {\rm d} \Omega = \int_{\Omega} \delta \theta \left\{ \nabla \cdot (\lambda \nabla \theta) + f \right\} {\rm d} \Omega \tag{14}
式 (14) を展開して、式 (15) を得ます。
\int_{\Omega} \delta \theta \; \rho c \; \dot{\theta} \; {\rm d} \Omega = \int_{\Omega} \delta \theta \; \nabla \cdot (\lambda \nabla \theta) {\rm d} \Omega + \int_{\Omega} \delta \theta \; f \; {\rm d} \Omega \tag{15}
ここで、ナブラの積の法則$\nabla \cdot (\phi A) = (\nabla \phi) \cdot A + \phi \nabla \cdot A$において、$A=\alpha \nabla \psi$とすると、式 (16) を得ます。
\nabla \cdot (\phi \; \alpha \nabla \psi) = (\nabla \phi) \cdot \alpha \nabla \psi + \phi \nabla \cdot \alpha \nabla \psi \tag{16}
式 (16) を移項して、式 (17) を得ます。
\phi \nabla \cdot \alpha \nabla \psi = \nabla \cdot (\phi \; \alpha \nabla \psi) - (\nabla \phi) \cdot \alpha \nabla \psi \tag{17}
式 (17) の関係から、式 (15) を変形し、式 (18) を得ます。
\int_{\Omega} \delta \theta \; \rho c \; \dot{\theta} \; {\rm d} \Omega = \int_{\Omega}
\left\{ \nabla \cdot (\delta \theta \; \lambda \nabla \theta) - (\nabla \delta \theta) \cdot \lambda \nabla \theta \right\}
{\rm d} \Omega + \int_{\Omega} \delta \theta \; f \; {\rm d} \Omega \tag{18}
式 (18) を展開し、式 (19) を得ます。
\int_{\Omega} \delta \theta \; \rho c \; \dot{\theta} \; {\rm d} \Omega
+ \int_{\Omega} (\nabla \delta \theta) \cdot \lambda \nabla \theta \; {\rm d} \Omega =
\int_{\Omega} \nabla \cdot (\delta \theta \; \lambda \nabla \theta) \; {\rm d} \Omega
+ \int_{\Omega} \delta \theta \; f \; {\rm d} \Omega \tag{19}
ここで、ガウスの定理を、式 (20) に示します。
\int_{\Omega} \nabla \cdot (\phi \nabla \psi) \; {\rm d} \Omega = \int_{\Gamma} \boldsymbol{n} \cdot (\phi \nabla \psi) \; {\rm d} \Gamma \tag{20}
式 (20) により、式 (19) の右辺第一項を変形し、式 (21) を得られます。
\int_{\Omega} \delta \theta \; \rho c \; \dot{\theta} \; {\rm d} \Omega
+ \int_{\Omega} \nabla \delta \theta \cdot \lambda \nabla \theta \; {\rm d} \Omega =
\int_{\Gamma} {\boldsymbol n} \cdot (\delta \theta \; \lambda \nabla \theta) \; {\rm d} \Gamma
+ \int_{\Omega} \delta \theta \; f \; {\rm d} \Omega \tag{21}
ここで、式 (21) の右辺第一項は、式 (22) のように変形できます。
\int_{\Gamma} {\boldsymbol n} \cdot (\delta \theta \; \lambda \nabla \theta) \; {\rm d} \Gamma \\
= \int_{\Gamma} \delta \theta \; \lambda \frac{\partial \theta}{\partial n} \; {\rm d} \Gamma \\
= \int_{\Gamma} \delta \theta \; q \; {\rm d} \Gamma \tag{22}
式 (21) と式 (22) より、式 (23) が得られます。
\int_{\Omega} \delta \theta \; \rho c \; \dot{\theta} \; {\rm d} \Omega
+ \int_{\Omega} \nabla \delta \theta \cdot \lambda \nabla \theta \; {\rm d} \Omega =
\int_{\Omega} \delta \theta \; f \; {\rm d} \Omega
+ \int_{\Gamma} \delta \theta \; q \; {\rm d} \Gamma \tag{23}
この式変形によって、有限要素法による離散化の準備ができました。
有限要素法による離散化
領域$\Omega$を、式 (24) のように有限要素近似することを考えます。具体的には、図4に示す計算領域から、図5、図6に示すような、有限要素離散化を行います。連続的な領域$\Omega$は、互いに重ならないよう充填された有限要素領域$\Omega^{(e)}$によって表現されます。有限要素領域$\Omega^{(e)}$は、離散点である節点の連結情報によって定義されます。
\Omega \simeq \Omega^{\rm FEM} = \bigcup_e^{n_{\rm elem}} \Omega^{(e)} \tag{24}
図4：計算領域
図5：有限要素離散化した後の計算領域（要素番号を図示）
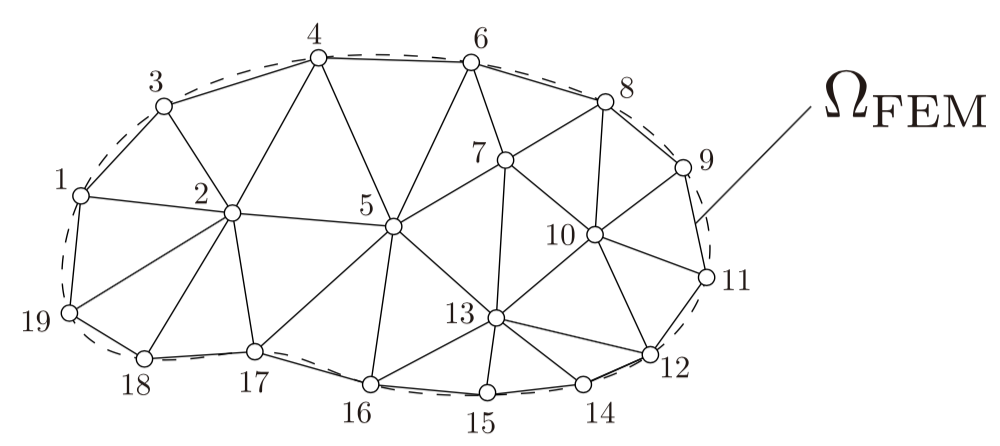図6：有限要素離散化した後の計算領域（節点番号を図示）
式 (24) より、領域$\Omega$の領域積分と境界積分は、それぞれで式 (25)、式 (26) 表されます。
\int_\Omega \; {\rm d} \Omega \simeq \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} \; {\rm d} \Omega^{(e)} \tag{25}
\int_\Gamma \; {\rm d} \Gamma \simeq \bigoplus_e^{n_{\rm elem}} \int_{\Gamma^{(e)}} \; {\rm d} \Gamma^{(e)} \tag{26}
ここで、$\bigoplus_e^{n_{\rm elem}}$は、有限要素法におけるアセンブリ記号です。図7にアセンブリ記号による計算例を示しました。この演算で実施したいのは、あるふたつの有限要素が表現する領域の和を得ることです。ある有限要素は、節点の連結情報で定義され、後述する手順によって節点数×自由度のサイズを有する密行列が得られます。その密行列の和が、有限要素が表現する領域の和をとることに対応することになり、有限要素を足し合わせた領域を構成する節点数×自由度のサイズを有する疎行列が得られます。
図7：有限要素法におけるアセンブリ記号（拡張和）の例
次に、ある要素$e$の領域内部の物理量$\phi^{(e)}$は、要素内の局所座標系$\boldsymbol{\xi}$と補間関数$\boldsymbol{N}$、節点物理量ベクトル$\boldsymbol{\phi}$を用いて、式 (27) で表されます。ここで、$i$はアインシュタイン記約におけるダミーインデックスです。
\phi^{(e)}(\boldsymbol{\xi}) = \boldsymbol{N} (\boldsymbol{\xi}) \; \boldsymbol{\phi} \\
= N_i (\boldsymbol{\xi}) \; \phi_i \tag{27}
以上の定義から、式 (23) は、式 (28) のように書き換えられます。
\bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} (N_i \delta \theta_i)^t \; \rho c \; N_j \dot{\theta}_j \; {\rm d} \Omega^{(e)}
+ \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} (\nabla N_i \delta \theta_i)^t \; \lambda \; \nabla N_j \theta_j \; {\rm d} \Omega^{(e)} = \\
\bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} (N_i \delta \theta_i)^t \; f_i \; {\rm d} \Omega^{(e)}
+ \bigoplus_e^{n_{\rm elem}} \int_{\Gamma^{(e)}} (N_i \delta \theta_i)^t \; q_i \; {\rm d} \Gamma^{(e)} \tag{28}
ここで、式 (28) から${\delta \theta _i}^t$をくくりだして、式 (29) を得ます。
{\delta \boldsymbol{\theta}}^t \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; \rho c \; N_j \dot{\theta}_j \; {\rm d} \Omega^{(e)}
+ {\delta \boldsymbol{\theta}}^t \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} (\nabla N_i)^t \; \lambda \; \nabla N_j \theta_j \; {\rm d} \Omega^{(e)} = \\
{\delta \boldsymbol{\theta}}^t \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; f_i \; {\rm d} \Omega^{(e)}
+ {\delta \boldsymbol{\theta}}^t \bigoplus_e^{n_{\rm elem}} \int_{\Gamma^{(e)}} {N_i}^t \; q_i \; {\rm d} \Gamma^{(e)} \tag{29}
式 (29) は任意の${\delta \boldsymbol{\theta}}^t$について成り立つので、式 (30) を得ます。
\bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; \rho c \; N_j \dot{\theta}_j \; {\rm d} \Omega^{(e)}
+ \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} (\nabla N_i)^t \; \lambda \; \nabla N_j \theta_j \; {\rm d} \Omega^{(e)} = \\
\bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; f_i \; {\rm d} \Omega^{(e)}
+ \bigoplus_e^{n_{\rm elem}} \int_{\Gamma^{(e)}} {N_i}^t \; q_i \; {\rm d} \Gamma^{(e)} \tag{30}
式 (30) の左辺を整理して、式 (31) を得ます。
\bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; \rho c \; N_j \; {\rm d} \Omega^{(e)} \; \boldsymbol{\dot{\theta}}
+ \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} (\nabla N_i)^t \; \lambda \; \nabla N_j \; {\rm d} \Omega^{(e)} \; \boldsymbol{\theta} = \\
\bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; f_i \; {\rm d} \Omega^{(e)}
+ \bigoplus_e^{n_{\rm elem}} \int_{\Gamma^{(e)}} {N_i}^t \; q_i \; {\rm d} \Gamma^{(e)} \tag{31}
ここで、$\boldsymbol{M}$、$\boldsymbol{K}$、$\boldsymbol{f}$を以下のように定義します。
\boldsymbol{M} = \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; \rho c \; N_j \; {\rm d} \Omega^{(e)} \tag{32}
\boldsymbol{K} = \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} (\nabla N_i)^t \; \lambda \; \nabla N_j \; {\rm d} \Omega^{(e)} \tag{33}
\boldsymbol{f} = \bigoplus_e^{n_{\rm elem}} \int_{\Omega^{(e)}} {N_i}^t \; f_i \; {\rm d} \Omega^{(e)} + \bigoplus_e^{n_{\rm elem}} \int_{\Gamma^{(e)}} {N_i}^t \; q_i \; {\rm d} \Gamma^{(e)} \tag{34}
式 (31)、式 (32)、式 (33)、式 (34)から、有限要素離散化された支配方程式 (35) を得ます。
\boldsymbol{M} \dot{\boldsymbol{\theta}} + \boldsymbol{K \theta} = \boldsymbol{f} \tag{35}
支配方程式 (35) は非定常熱伝導解析を示しており、定常熱伝導解析の場合は、時間微分項である左辺第一項を無視することで支配方程式 (36) が得られます。
\boldsymbol{K \theta} = \boldsymbol{f} \tag{36}
ここで、時間離散化した支配方程式 (35) や支配方程式 (36) は、正定値疎行列を係数行列にもつ連立一次方程式となっています。有限要素解析の場合、この式を数値的に解くことになります。連立一次方程式を数値的に解く手法は様々ありますが、この概要については、本記事後編で説明します。
今後の執筆方針
- 有限要素離散化から得られた行列が、正定値疎行列となることを説明します
- 連立一次方程式を解く手法（直接法、反復法）の概略を説明します
- 反復法に関して、正定値行列が A-直交な基底ベクトルを有することを説明したあと、このベクトルを用いて解を反復的に求める手法のひとつである、共役勾配法について説明します