EMアルゴリズムを使って多峰型分布をモデル化してみる

概要

標本から得られた分布が多峰型であったとき, 単純なガウス分布でモデル化するのは適切ではありません.
多峰型の分布は複数のガウス分布を組み合わせた混合ガウス分布を使ってモデル化することができます.
この記事ではEMアルゴリズムを使って, 混合ガウス分布のパラメータを決定する例を紹介します.

まずは単峰型分布から

最尤推定

標本を$x_n (n=1,…,N)$とします.
ガウス分布の最尤推定によって, 平均と分散を以下の形で求めることができます.

\mu_{ML}=\frac{1}{N}\sum_{n=1}^N x_n \\\
\sigma^2_{ML}=\frac{1}{N-1}\sum_{n=1}^N (x_n-\mu_{ML})^2

分散の値は不偏推定量を用いています.

手順

1. 平均3.0, 分散2.0のガウス分布から10000個の標本を生成する.
2. 得られた標本から最尤推定を用いて平均と分散を推定する.

ソースコード

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
import math

#ヒストグラムをプロットする関数
def draw_hist(xs, bins):
    plt.hist(xs, bins=bins, normed=True, alpha=0.5)

#与えられた標本から最尤推定を用いて平均と分散を求める関数
def predict(data):
    mu = np.mean(data)
    var = np.var(data, ddof=1)  #不偏推定量を用いる
    return mu, var

def main():
    #平均mu, 標準偏差stdのガウス分布に従う標本をN個生成する
    mu = 3.0
    v = 2.0
    std = math.sqrt(v)
    N = 10000
    data = np.random.normal(mu, std, N)
    #最尤推定を行い, 平均と分散を求める
    mu_predicted, var_predicted = predict(data)
    #分散の値から標準偏差を求める
    std_predicted = math.sqrt(var_predicted)
    print("original: mu={0}, var={1}".format(mu, v))
    print(" predict: mu={0}, var={1}".format(mu_predicted, var_predicted))

    #結果のプロット
    draw_hist(data, bins=40)
    xs = np.linspace(min(data), max(data), 200)
    norm = mlab.normpdf(xs, mu_predicted, std_predicted)
    plt.plot(xs, norm, color="red")
    plt.xlim(min(xs), max(xs))
    plt.xlabel("x")
    plt.ylabel("Probability")
    plt.show()


if __name__ == '__main__':
    main()

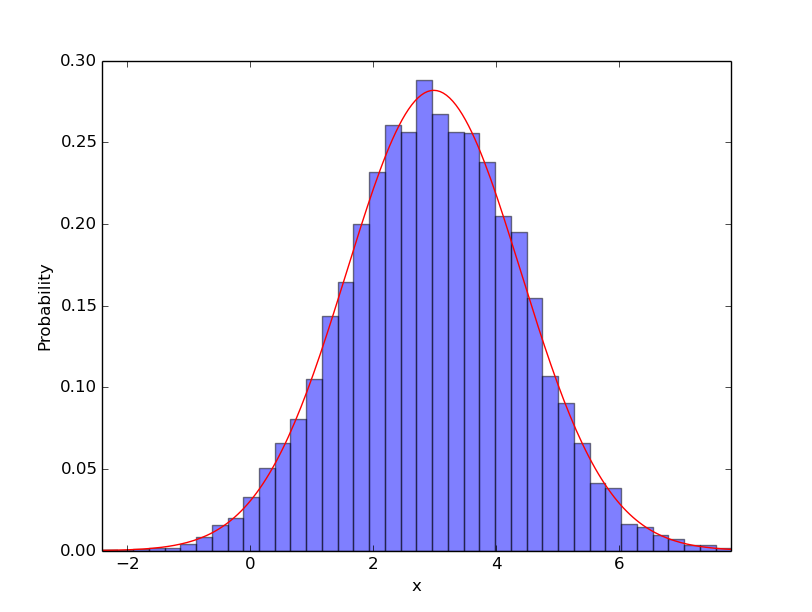
実行結果

ヒストグラム(青)は標本を表し, 赤線は推定された値を用いてモデル化されたガウス分布を表します.

original: mu=3.0, var=2.0
 predict: mu=2.98719564872, var=2.00297779707

適切なガウス分布のモデルを求めることができました.

双峰型の分布

データセット

Old Faithful - 間欠泉データを使います. 以下のリンクからダウンロードできます.
Old Faithful
データセットの中身は以下のようになっています.

• 1列目: 直近の噴出継続時間(分)
• 2列目: 次回の噴出までの待ち時間(分)

今回は直近の噴出継続時間(1列目)だけを標本として用いることにします.この標本から以下の双峰型分布が得られました.

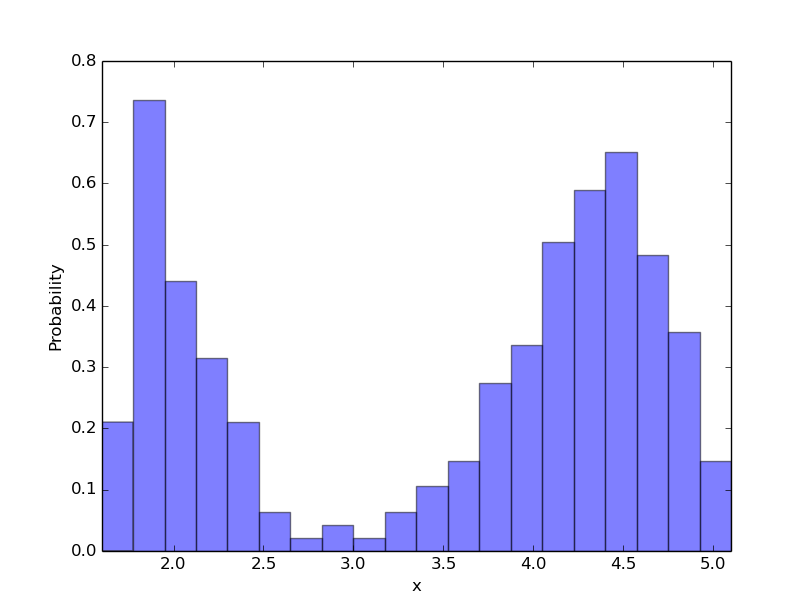
分布を見た感じ単純なガウス分布ではモデル化できなさそうです.
ここで, 2つのガウス分布を組み合わせた混合ガウス分布を使ってモデル化しようと思います.
モデル化する際には平均$\mu_1, \mu_2$, 分散$\sigma_1^2, \sigma_2^2$, 混合確率$\pi$のパラメータを決定する必要があります.
ガウス分布を$\phi(x|\mu, \sigma^2)$とすると, 混合ガウス分布は以下の式で与えられます.

y=(1-\pi)\phi(x|\mu_1, \sigma^2_1)+\pi\phi(x|\mu_2, \sigma^2_2)

EMアルゴリズム

ガウス分布の平均と分散は尤度関数の最大化を解析的に解くことで求めることができます(PRMLの§2.3.4を参照).
しかし混合ガウス分布の尤度関数の最大化は解析的に解くことが難しいため, 最適化手法の一つであるEMアルゴリズムを用いて最大化を行います.
EMアルゴリズムはEステップとMステップの2つを繰り返し行うアルゴリズムです.

• E(Expectation)ステップ: 負担率を計算する.
• M(Maximization)ステップ: 重み付きの平均と分散を計算する.

詳しいアルゴリズムの内容はThe Elements of Statistical Learningの§8.5を参照してください.
英語版のPDFは無料でダウンロードすることができます.

ソースコード

# -*- coding: utf-8 -*-

import numpy as np
import math
import random
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab

#平均m, 分散vのガウス分布
def gaussian(x, m, v):
    p = math.exp(- pow(x - m, 2) / (2 * v)) / math.sqrt(2 * math.pi * v)
    return p

#Eステップ
def e_step(xs, ms, vs, p):
    burden_rates = []
    for x in xs:
        d = (1 - p) * gaussian(x, ms[0], vs[0]) + p * gaussian(x, ms[1], vs[1])
        n = p * gaussian(x, ms[1], vs[1])
        burden_rate = n / d
        burden_rates.append(burden_rate)
    return burden_rates


#Mステップ
def m_step(xs, burden_rates):
    d = sum([1 - r for r in burden_rates])
    n = sum([(1 - r) * x for x, r in zip(xs, burden_rates)])
    mu1 = n / d

    n = sum([(1 - r) * pow(x - mu1, 2) for x, r in zip(xs, burden_rates)])
    var1 = n / d

    d = sum(burden_rates)
    n = sum([r * x for x, r in zip(xs, burden_rates)])
    mu2 = n / d

    n = sum(r * pow(x - mu2, 2) for x, r in zip(xs, burden_rates))
    var2 = n / d

    N = len(xs)
    p = sum(burden_rates) / N

    return [mu1, mu2], [var1, var2], p


#対数尤度関数
def calc_log_likelihood(xs, ms, vs, p):
    s = 0
    for x in xs:
        g1 = gaussian(x, ms[0], vs[0])
        g2 = gaussian(x, ms[1], vs[1])
        s += math.log((1 - p) * g1 + p * g2)
    return s

#ヒストグラムをプロットする関数
def draw_hist(xs, bins):
    plt.hist(xs, bins=bins, normed=True, alpha=0.5)

def main():
    #データセットの1列目を読み込む
    fp = open("faithful.txt")
    data = []
    for row in fp:
        data.append(float((row.split()[0])))
    fp.close()
    #mu, vs, pの初期値を設定する
    p = 0.5
    ms = [random.choice(data), random.choice(data)]
    vs = [np.var(data), np.var(data)]
    T = 50  #反復回数
    ls = []  #対数尤度関数の計算結果を保存しておく
    #EMアルゴリズム
    for t in range(T):
        burden_rates = e_step(data, ms, vs, p)
        ms, vs, p = m_step(data, burden_rates)
        ls.append(calc_log_likelihood(data, ms, vs, p))

    print("predict: mu1={0}, mu2={1}, v1={2}, v2={3}, p={4}".format(
        ms[0], ms[1], vs[0], vs[1], p))
    #結果のプロット
    plt.subplot(211)
    xs = np.linspace(min(data), max(data), 200)
    norm1 = mlab.normpdf(xs, ms[0], math.sqrt(vs[0]))
    norm2 = mlab.normpdf(xs, ms[1], math.sqrt(vs[1]))
    draw_hist(data, 20)
    plt.plot(xs, (1 - p) * norm1 + p * norm2, color="red", lw=3)
    plt.xlim(min(data), max(data))
    plt.xlabel("x")
    plt.ylabel("Probability")

    plt.subplot(212)
    plt.plot(np.arange(len(ls)), ls)
    plt.xlabel("step")
    plt.ylabel("log_likelihood")
    plt.show()

if __name__ == '__main__':
    main()

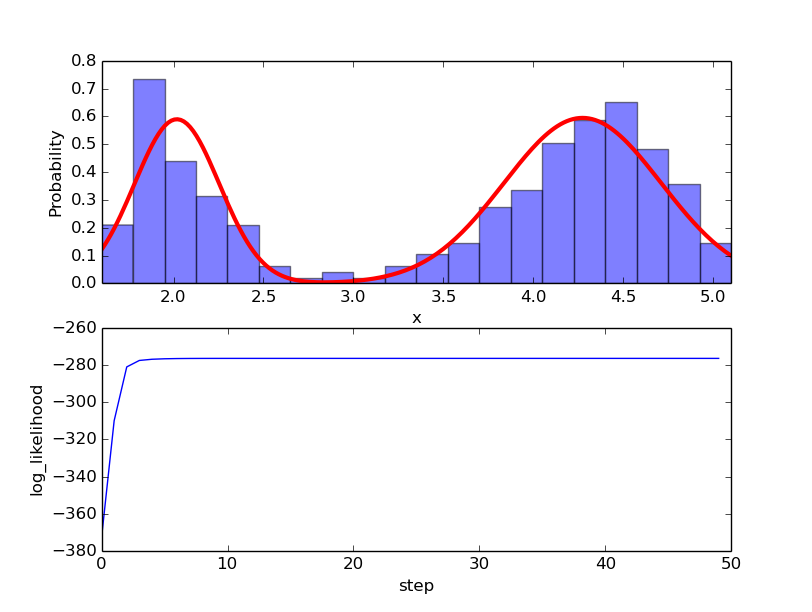
実行結果

predict: mu1=2.01860781706, mu2=4.27334342119, v1=0.0555176191851, v2=0.191024193785, p=0.651595365985

上の図はデータセットから得られた標本を混合ガウス分布でモデル化した結果を表しています.
下の図はEMアルゴリズムを繰り返すことで対数尤度が大きくなっていく様子を表しています.

その他

EMアルゴリズムにおける初期値

平均はランダムに選ばれた標本, 分散は標本の分散, 混合確率は0.5を初期値として用いました.
初期値の選び方は色々考えられますが, これだけで論文になってしまう(?)話のようです.

多峰型分布について

今回の標本は双峰型分布なので, ガウス分布を2つ組み合わせました.
当然3つ以上のガウス分布を組み合わせることもできますが, 決定する必要のあるパラメータの数は増えていきます.

データセットの次元について

今回は1次元の標本を用いましたが, 多変量のガウス分布についてもEMアルゴリズムを用いることができます.
多変量のガウス分布は, 1次元のガウス分布に比べて決定するパラメータが非常に多くなります(平均, 共分散行列).