こんにちは、しゅれぬこ(@syurenuko)です。
先日、効果検証で傾向スコアを用いた補正をする機会があったのですが、
「傾向スコアを算出するための機械学習とAdversarial Validationって目的が異なるだけで中身のやってること同じなのでは?」
ということに気付き、ABテストにおいてセレクションバイアスの原因となってる可能性がある変数をEDA(探索的データ分析)抜きで推定できないか気になったので実験してみました。
ABテストは介入群と対照群のデータ分布の傾向が一致していることが望ましいので、この方法が上手くいけば何らかの原因で生じた2群間での分布の不一致を簡単にチェックできそうです。
今回はBigQuery上でSQLライクで簡単にモデル構築ができるBigQueryMLを用いて実装していきます。効果検証の重要性から書いているので、Adversarial Validationの説明や実装例だけ見たい方は適宜飛ばしてください。
効果検証の重要性
ある施策が有効かどうかを判定するのに使われる代表的な手法がABテストです。
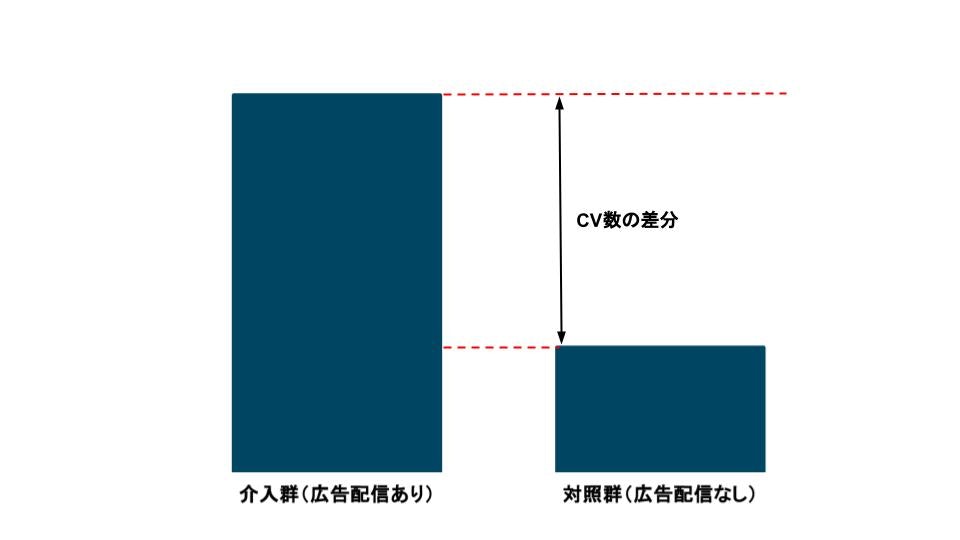
以下の図のように施策ありの群(介入群)と施策なしの群(対照群)の2つに分け、差分から施策に効果があったかどうかを判断します。
例 : 広告配信が交通チケット予約サイトのCV(コンバージョン)向上に繋がるかどうかのABテスト
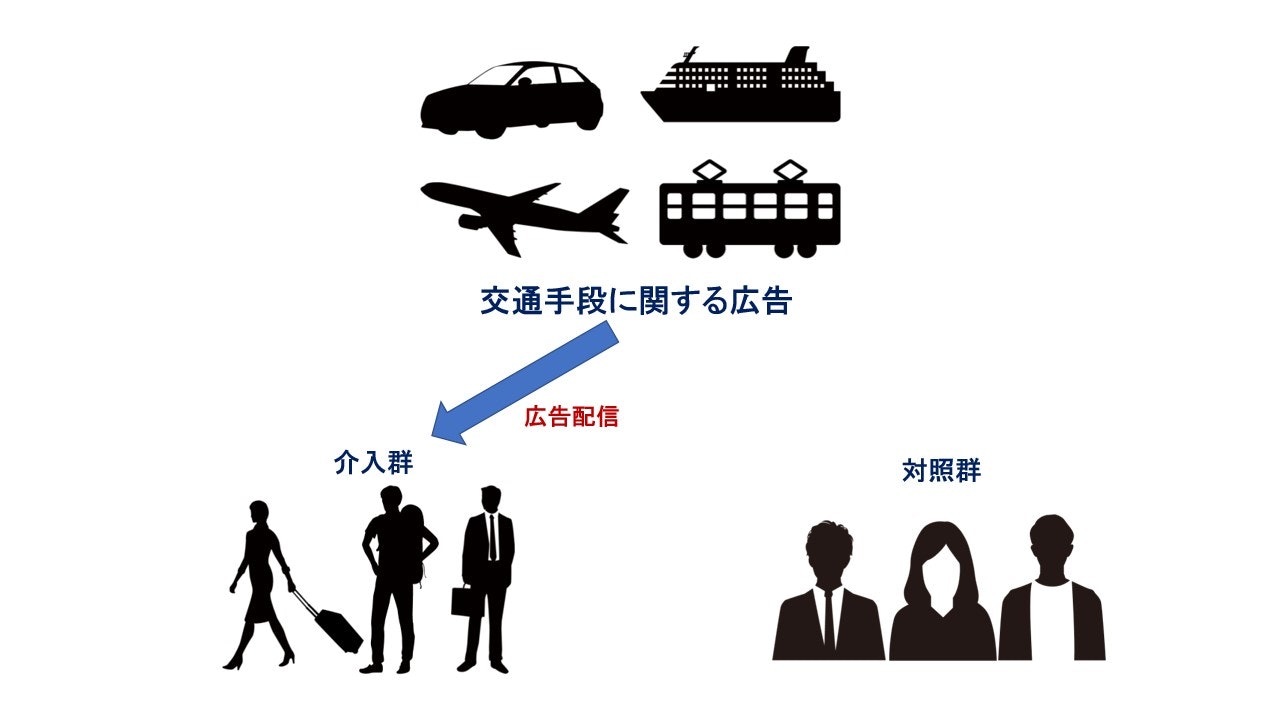
このABテストから広告配信はCVを向上させることがわかりました。
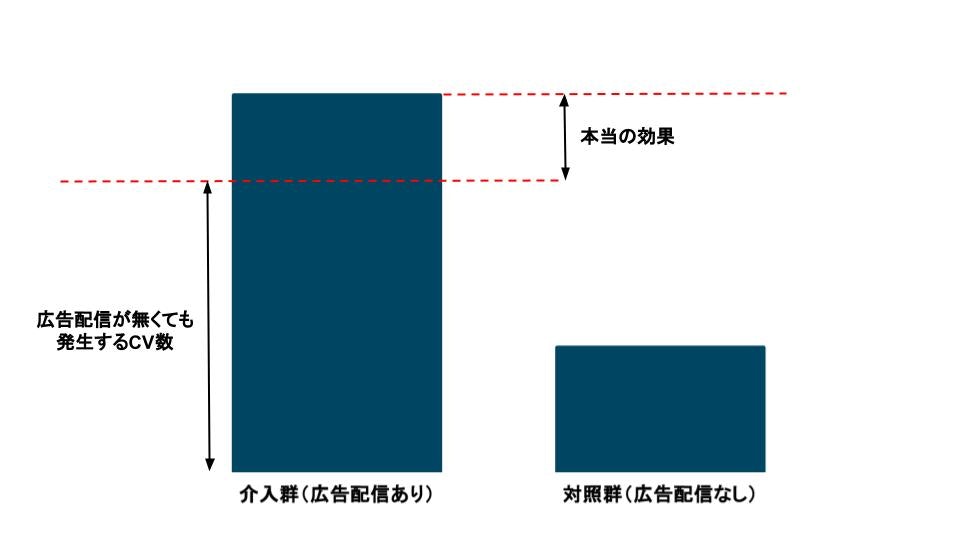
しかし、このABテストでは介入群の方が対照群よりも「旅行好き」のユーザーが多かったことが判明したとします。
旅行好きのユーザーは交通手段に関する広告配信がなくても、旅行のために交通チケットを予約する可能性が高いことから、広告配信の効果を過大評価している可能性に注意を払う必要があります。
つまり、「旅行好き」という交絡因子の偏りからセレクションバイアスが発生している状態です。
以上のような理由からABテストでは無作為にどちらかの群に振り分けることで、2群間で偏りを発生しないようにするのが望ましいとされています。(RCT(Randomized Controlled Trial):ランダム化比較実験)
しかし実際の現場では、効果のありそうなユーザーにターゲットを絞った施策が行われるなど、コストを始めとするビジネス上の事情からRCTが難しい場合があります。
傾向スコアによる補正
このようなバイアスが生じる場合に補正する代表的な手法が傾向スコアを用いた補正です。
介入群を1、対照群を0を目的変数とする2値分類を解き、ユーザーが介入群に近いのかを0〜1の範囲の確率値(傾向スコア)で表現します。
ここでは詳しく解説しませんが、傾向スコアが近いユーザー同士で効果を比較したり(傾向スコアマッチング)、傾向スコアの逆数の重みを取って補正する(IPW補正)などが代表的な補正方法です。
Adversarial Validation
Adversarial Validationは、kaggleなどの機械学習コンペの上位解法でたまに見る手法です。
参考記事
Kaggleで役立つAdversarial Validationとは
Adversarial Validationを用いた特徴量選択 - u++の備忘録
機械学習では予測精度の観点から学習データとテストデータの分布が一致している、つまり学習データとテストデータの判別ができない状態が望ましいとされています。
そこで学習データを1、テストデータを0を目的変数とする2値分類を解き、AUCが0.5付近になるかを確認する手法がAdversarial Validationです。AUC 0.5は学習データとテストデータを判別できていない(ランダム推論と同じ)状態なので2群間のデータ分布の傾向が一致していると見ることができますが、AUCが0.7や0.8など高い値を取れば「学習データとテストデータを判別できている」ことになります。
また、特徴量重要度を出すことで「どの変数が学習データとテストデータを判別できる材料になっているか(データ分布の傾向が異なっている特徴量はどれか)」を確認することができます。もし特徴量重要度が異常に高い変数があれば該当する変数をデータから削除するなどの処理を行ってから学習させます。
セレクションバイアスの発生箇所を推定する方針
長くなりましたが、以上の説明から
・傾向スコア算出における機械学習
→「介入群、対照群を目的変数とする2値分類を解き、0~1の範囲の確率値(傾向スコア)を補正に使用する」
・Adversarial Validationにおける機械学習
→「学習データ、テストデータを目的変数とする2値分類を解き、AUCが0.5付近か確認する&特徴量重要度から分布の異なる特徴量を見出す」
と、目的が異なるだけでやっていることの中身は同じことがわかったと思います。
そこで「傾向スコア算出における機械学習にAdversarial Validationの考えを用いることで2群間のデータ分布が異なる変数(=セレクションバイアスの原因となり得る変数)を見抜こう」というのが今回の試みです。
一般的に傾向スコアを算出する際に使われるモデルはロジステック回帰ですが、特徴量重要度を確認するためにGBDTを用いて2値分類を解きます。
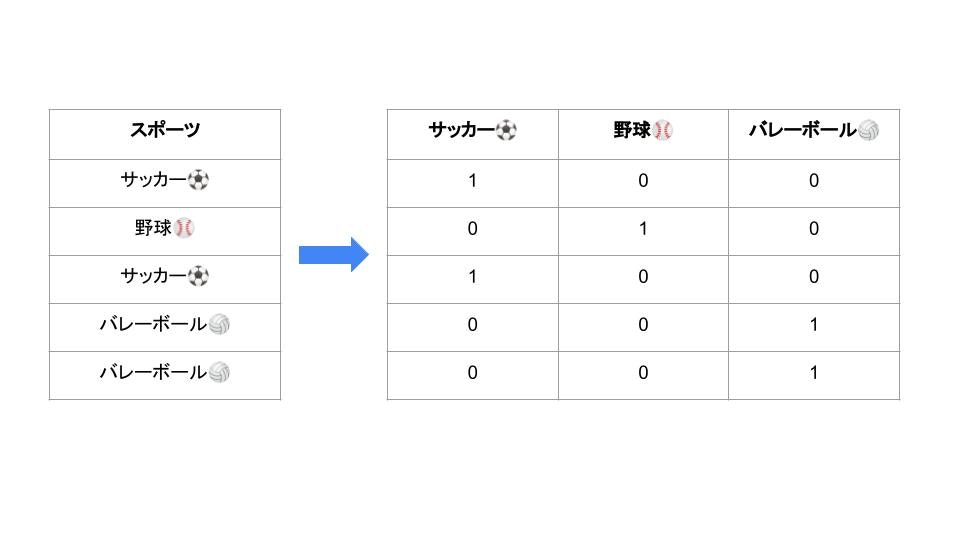
変数にカテゴリ変数が含まれる場合は「カテゴリ変数のどの変数で分布の違いが発生しているのか」が分かるように、以下の図のようにOne Hot Encodingの要領で、0 or 1のダミー変数に変換します。
使用するデータセット
今回は岩波データサイエンスvol.3のCM接触の因果効果推定のデータセットを使っていきます。
岩波データサイエンス Vol.3(岩波書店)
https://github.com/iwanami-datascience/vol3/tree/master/kato%26hoshino
データセットはゲームアプリのCM接触の有無がゲーム利用時間に影響したかどうかを調べるためのもので、変数(共変量)は居住地や年齢、性別などのユーザー属性になっています。(カテゴリ変数はすでにダミー変数化されています)
CM接触の有無で単純比較した場合「CM接触がある方がゲーム利用時間が短い」という不自然な結果になっており、バイアスの存在でCM接触を過小評価している可能性が考えられます。
この記事では扱いませんが、傾向スコアを用いて効果検証する試みは以下の記事が詳しいです。
岩波データサイエンスvol.3のデータで遊ぼう
BigQueryMLを用いて特徴量重要度を算出する
さっそく介入群を1、対照群を0とする2値分類をBigQueryMLで解き、特徴量重要度を算出していきます。
2値分類を解くための機械学習モデル(GBDT)の実装は以下のようにとてもシンプルに書けます。(変数の説明を兼ねているのであえて変数名を全列挙してますが、SELECT文の中身は"*"や"EXCEPT"等を使えばさらに短く書くことが可能です)
CREATE OR REPLACE MODEL
iwanami_vol3.model_GBDT
OPTIONS(
MODEL_TYPE = "BOOSTED_TREE_CLASSIFIER", -- GBDT(XGboost)の2値分類
input_label_cols = ["cm_dummy"] -- 目的変数をここで指定する
) AS
SELECT
-- 目的変数(cm_dummy)
cm_dummy, -- CM接触の有無(介入群 or 対照群)
-- 変数(共変量)
area_kanto, -- 居住地が関東エリア
area_keihan, -- 居住地が京浜エリア
area_tokai, -- 居住地が東海エリア
area_keihanshin, -- 居住地が京阪神エリア
age, -- 年齢
sex, -- 性別(男性=1)
marry_dummy, -- 結婚の有無(既婚=1)
child_dummy, -- 子供の有無(子供あり=1)
job_dummy1, -- 職業:正社員・公務員
job_dummy2, -- 職業:自営業・個人事業主
job_dummy3, -- 職業:派遣社員・契約社員
job_dummy4, -- 職業:その他職業
job_dummy5, -- 職業:パート・アルバイト
job_dummy6, -- 職業:専業主婦・専業主夫
job_dummy7, -- 職業:学生
job_dummy8, -- 職業:無職
inc, -- 年間収入
pmoney, -- 1月あたりのお小遣い
fam_str_dummy1, -- 家族構成:単身
fam_str_dummy2, -- 家族構成:夫婦のみ
fam_str_dummy3, -- 家族構成:2世代同居
fam_str_dummy4, -- 家族構成:3世代同居
fam_str_dummy5, -- 家族構成:その他
TVwatch_day, -- 1日当たりの平均TV視聴時間
T, -- 13~19歳の男女
F1, -- 20~34歳の女性
F2, -- 35~49歳の女性
F3, -- 50歳以上の女性
M1, -- 20~34歳の男性
M2, -- 35~49歳の男性
M3 -- 50歳以上の男性
FROM
`syurenuko_datasets.iwanami_vol3.q_data_x`
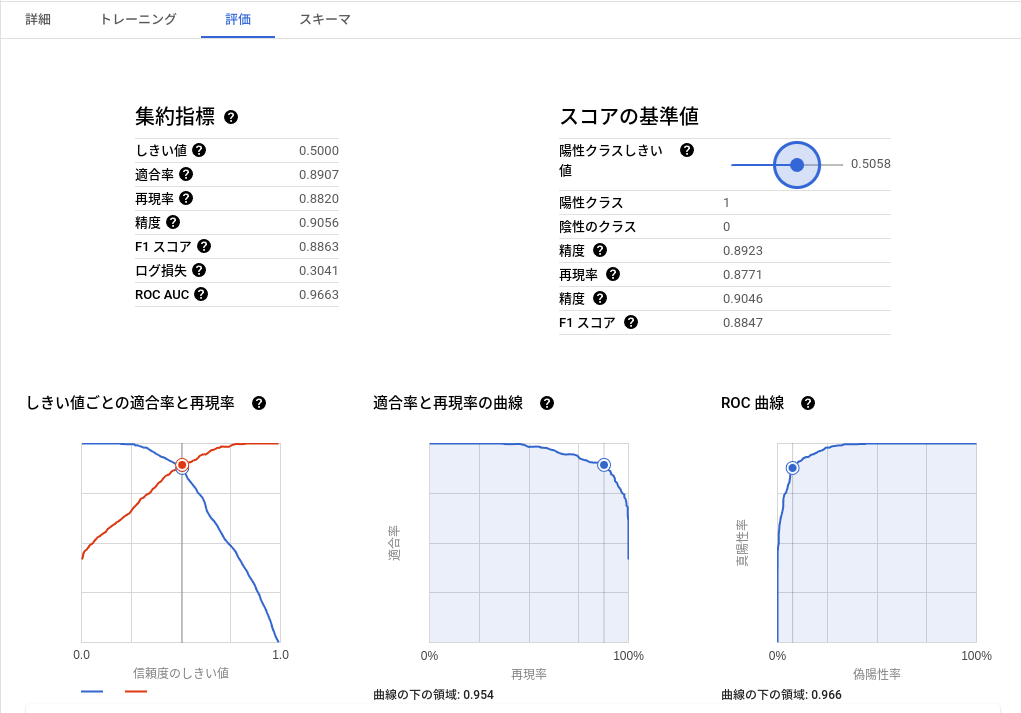
クエリを実行してしばらく待つと学習が完了し、結果タブから評価を見れるようになります。
AUCが0.966となっているので機械学習モデル(GBDT)は介入群と対照群を判別出来ているっぽいです。
保存してある学習モデルを呼び出して、特徴量重要度を算出し降順ソートします。
SELECT
feature, importance_gain
FROM
ML.FEATURE_IMPORTANCE(MODEL `iwanami_vol3.model_GBDT`)
ORDER BY importance_gain DESC
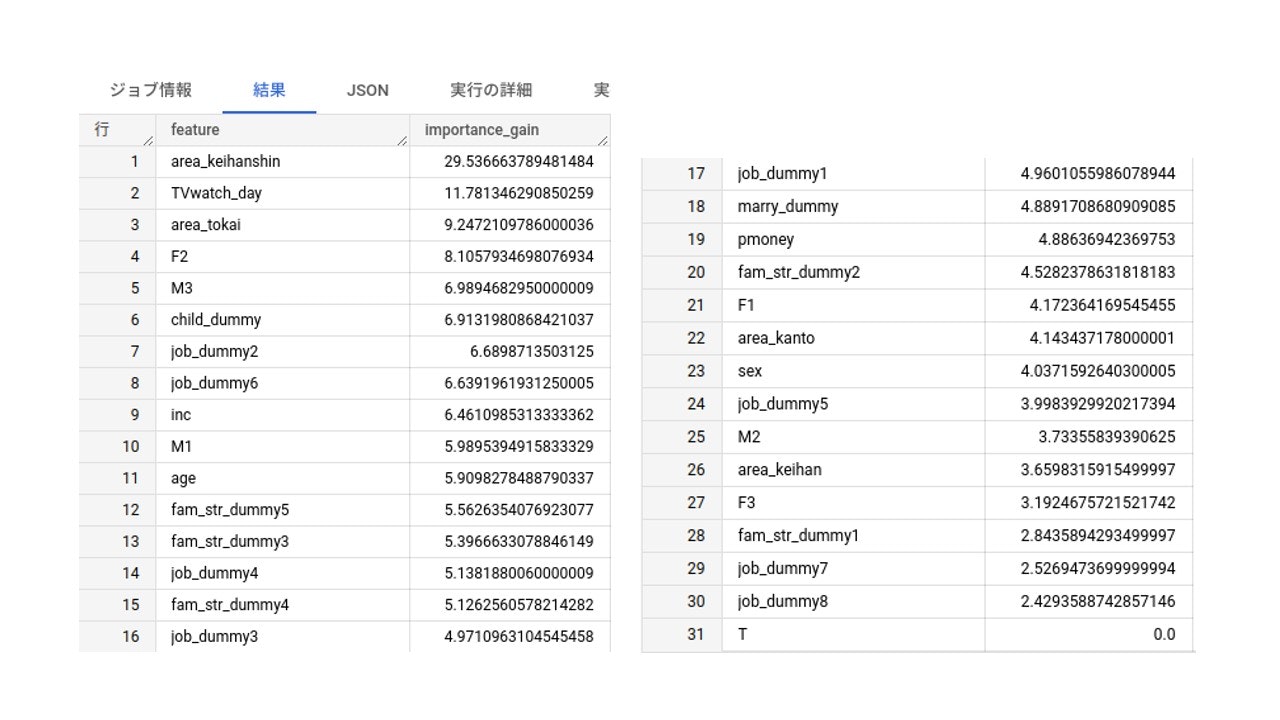
特徴量重要度が表示されました。
area_keihanshin(居住地が京阪神エリア) と TVwatch_day(1日当たりの平均TV視聴時間) などの特徴量重要度の高さが目立っています。特徴量重要度が0の変数はTだけでした。
注意
GBDTの結果を傾向スコアとしてIPW補正することもできますが、GBDTの出力は両端に偏った分布になりやすく傾向スコアの逆数をとった時の重みが大きくなってしまいます。よって、IPW補正用の傾向スコアを求める場合はセオリー通りにロジスティック回帰を使うのが無難です。(私の手元では重みが爆発してしまい上手く補正できませんでした)
参考記事
傾向スコアと機械学習とprobability calibrationの話 - rmizutaの日記
統計的因果推論(3): 傾向スコア算出を機械学習に置き換えてみると - 渋谷駅前で働くデータサイエンティストのブログ
介入群と対照群でデータ分布を確認
特徴量重要度が高い変数で、データ分布の傾向の違いが発生しているのかを確認します。
一番高い変数から順番に見ていきましょう。
ダミー変数用の可視化コード
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.rcParams.update({'font.size': 14})
data = pd.read_csv('q_data_x.csv')
data['cm_dummy_label'] = data['cm_dummy'].replace({0: '対照群', 1: '介入群'})
FEATURE = "area_keihanshin" # 任意のダミー変数を指定
labels_category = [0, 1]
plt.figure(figsize=(8, 5))
sns.countplot(x="cm_dummy_label", hue=FEATURE, data=data, hue_order=labels_category)
plt.title(f"{FEATURE}の各群における分布")
plt.legend(title=FEATURE, loc='upper right')
plt.show()
fig, ax = plt.subplots(1, 2, figsize=(8, 5), facecolor='white')
labels = ['対照群', '介入群']
for i, label in enumerate(labels):
value_counts = data[FEATURE][data["cm_dummy_label"] == label].value_counts()
ax[i].pie(value_counts, labels=labels_category, autopct='%.1f%%')
ax[i].set_title(label)
plt.show()
連続変数用の可視化コード
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.rcParams.update({'font.size': 14})
data = pd.read_csv('q_data_x.csv')
data['cm_dummy_label'] = data['cm_dummy'].replace({0: '対照群', 1: '介入群'})
labels = ['対照群', '介入群']
plt.figure(figsize=(8, 5))
sns.histplot(x="cm_dummy_label", hue="cm_dummy_label", data=data, hue_order=labels)
plt.show()
FEATURE = "TVwatch_day" #age, inc, pmoney
bin_range = range(0, 50000, 1000) #ここは変数によって上手い具合に変える
alpha_value = 0.5
plt.figure(figsize=(8, 5))
for label in labels:
plt.hist(data.loc[data["cm_dummy_label"] == label, FEATURE], bins=bin_range, alpha=alpha_value, label=label)
plt.legend()
plt.show()
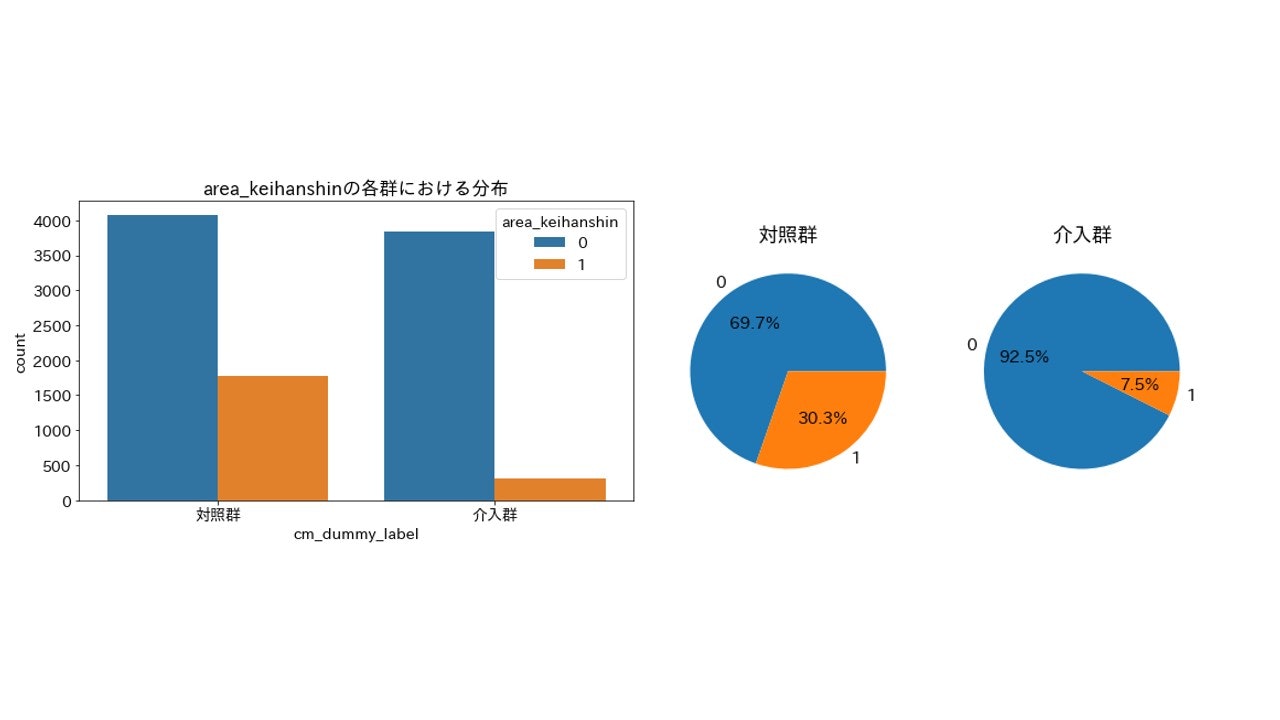
area_keihanshin(居住地が京阪神エリア)
importance_gain = 29.536663789481484
TVwatch_day(1日当たりの平均TV視聴時間)
importance_gain = 11.781346290850259
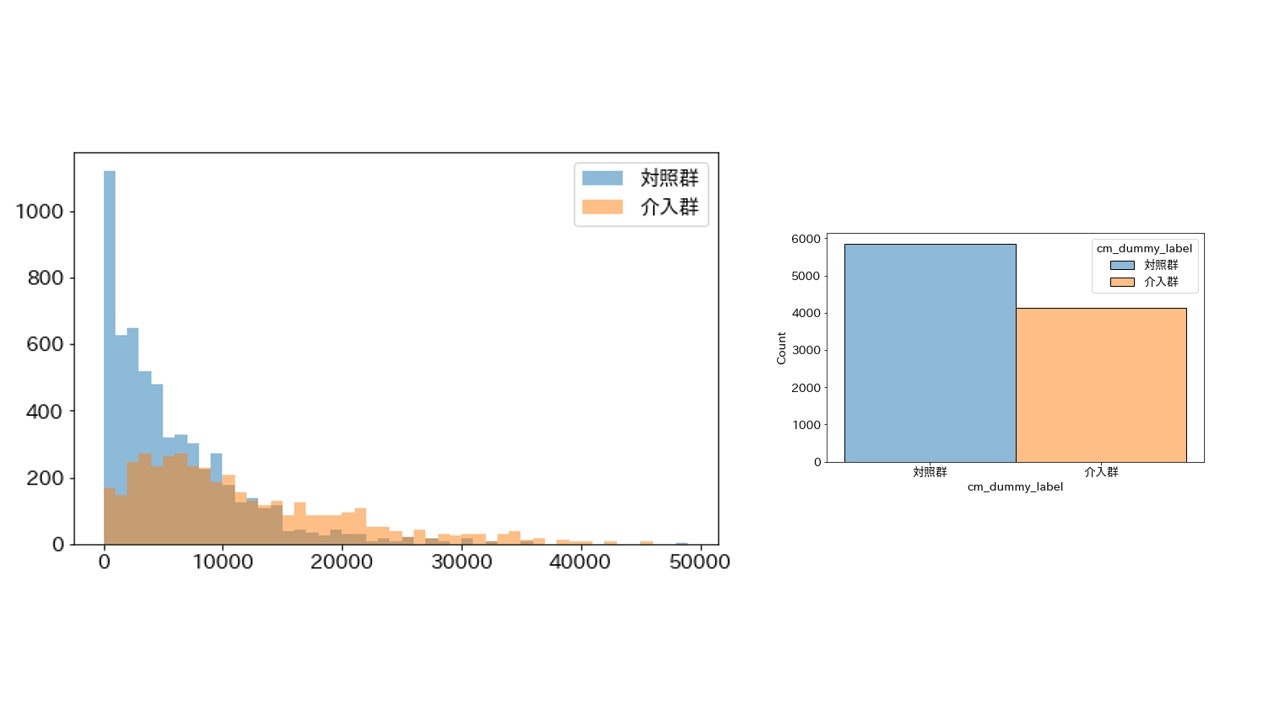
area_tokai(居住地が東海エリアか)
importance_gain = 9.2472109786000036
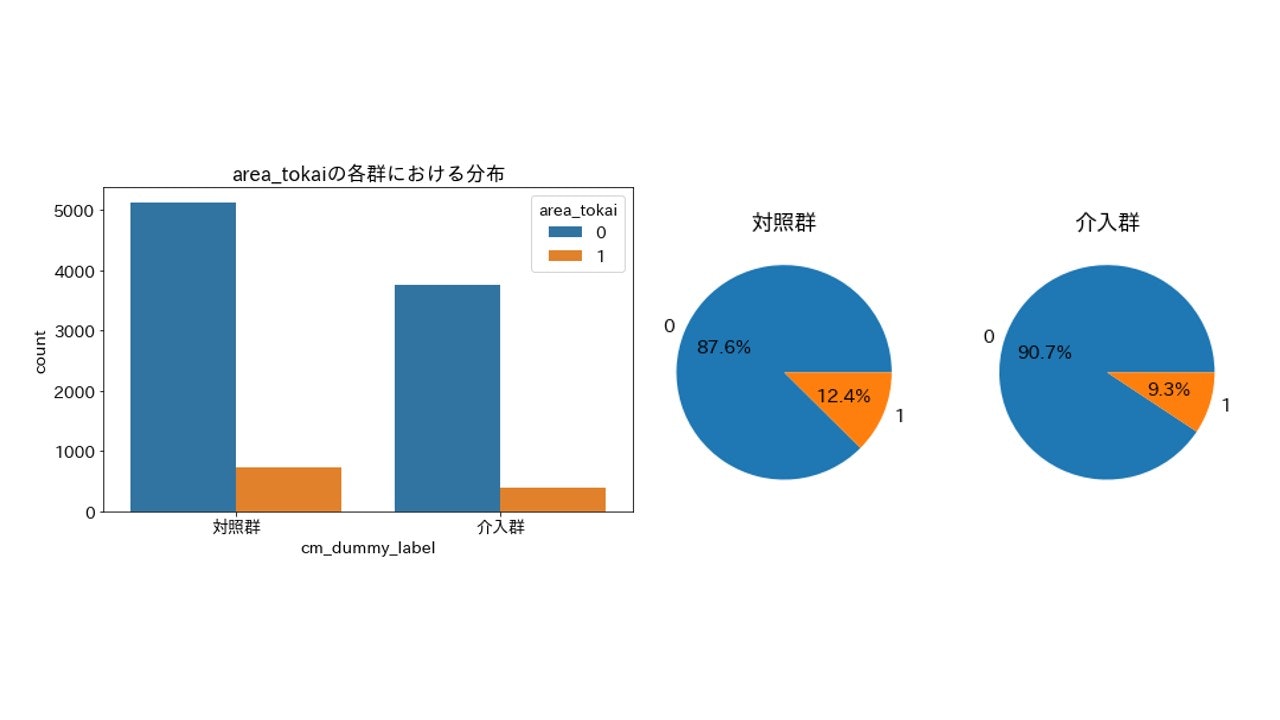
F2(20~34歳の女性)
importance_gain = 8.1057934698076934
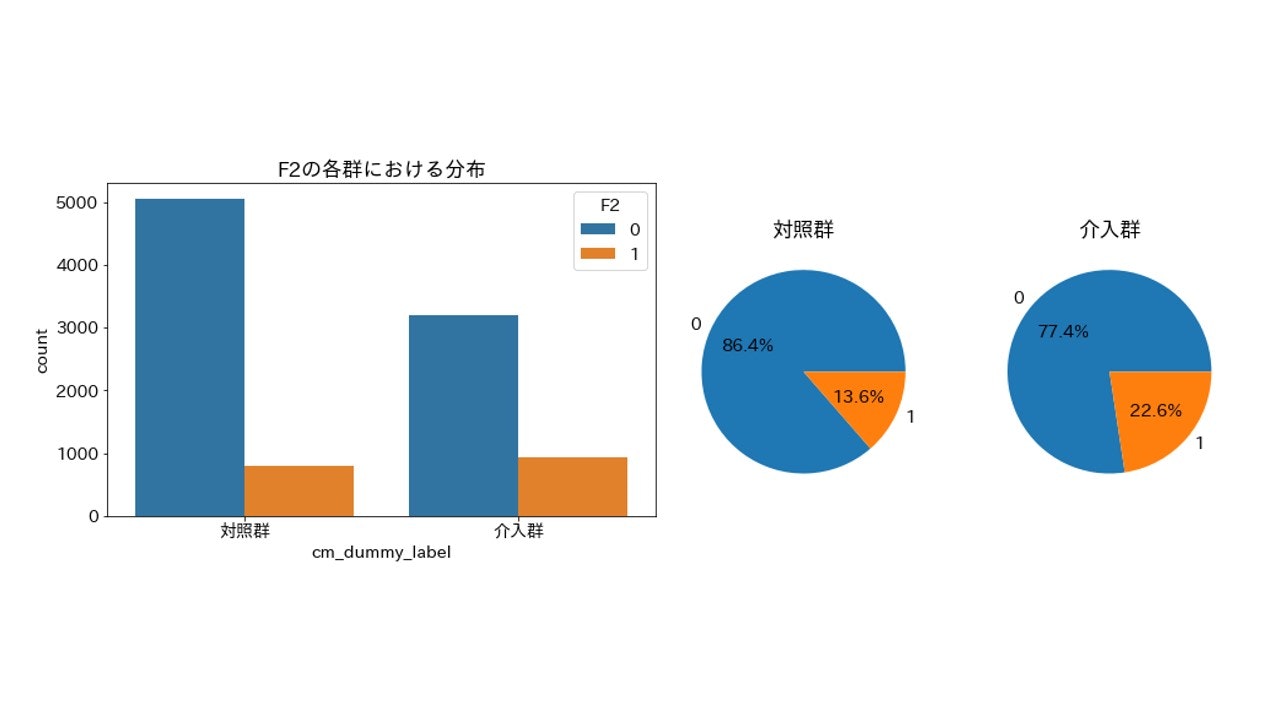
M3(50歳以上の男性)
importance_gain = 6.9894682950000009
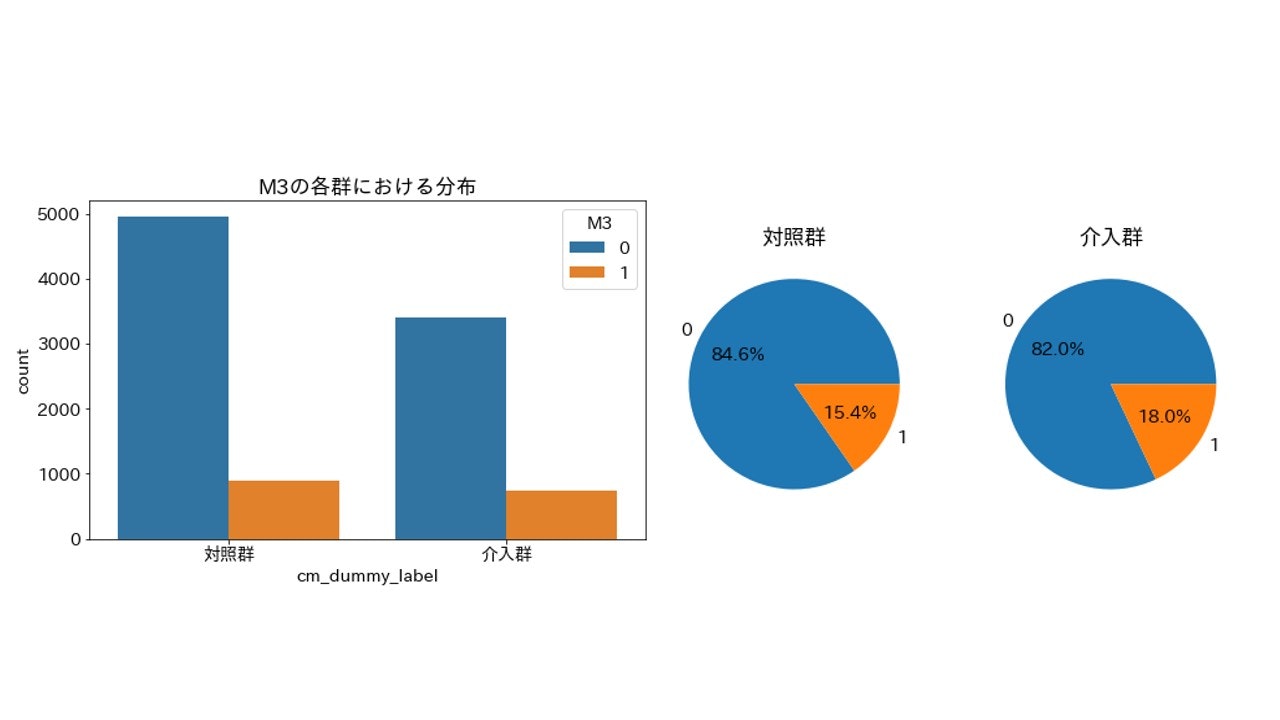
とりあえず上位5つの変数を可視化してみましたが、程度に差こそあれ偏りは発生しているようです。特に上位2つarea_keihanshinとTVwatch_dayは偏りがはっきりわかります。
31個も変数があるので今回はすべての変数のグラフをここには載せませんが、確認したところ特徴量重要度が0であるT以外の変数で(程度の差はあれど)偏りが発生していました。
T(13~19歳の男女)
importance_gain = 0
2群間で割合が一致
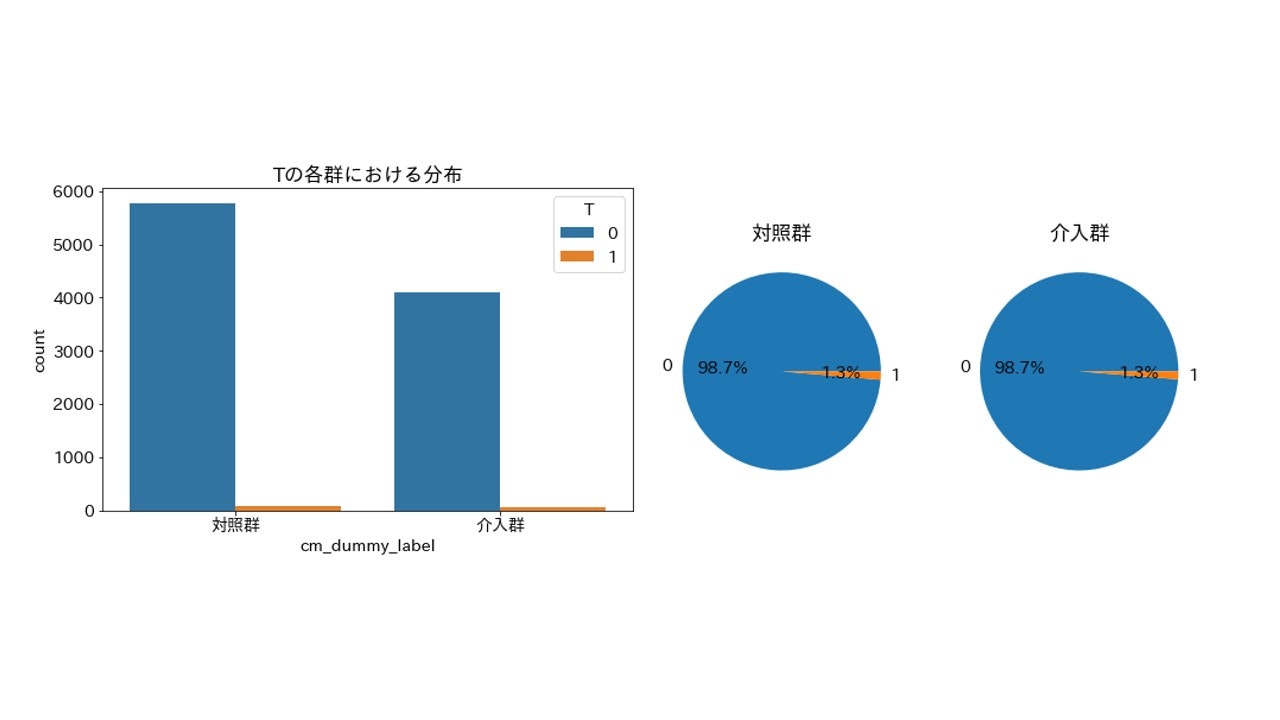
「データ分布が顕著に異なる変数は特徴量重要度の上位になっていることから高確率で見抜けている」...と結論付けたかったんですが、20ポイント近く割合が異なる area_keihan(居住地が京浜エリア) が下位だったので、特徴量重要度(importance_gain)の数字の大きさにどこまで意味があるのかは調べる余地がありそうです。
area_keihan(居住地が京浜エリア)
importance_gain = 3.6598315915499997
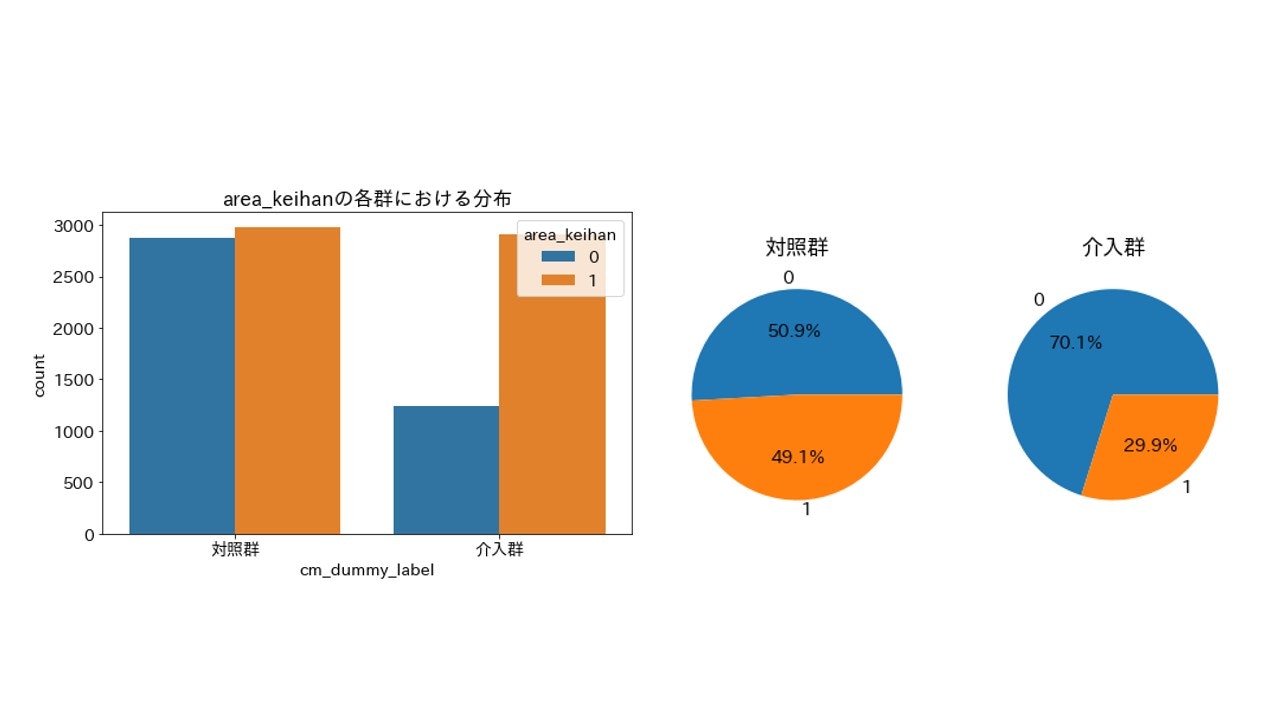
本来であればEDA(探索的データ分析)で変数ごとに分布を確認する必要があります。しかし今回はAdversarial Validationの考えを用いることでデータ分布の傾向が異なる変数の見当を大方付けることができました。変数が少ないので今回の実験ではあまり恩恵はないかもしれませんが、変数が数百数千と膨大な場合に有用になる手法だと思います。
交絡因子になりそうな変数で特徴量重要度が高い場合はセレクションバイアスが発生している可能性に注意する必要があります。今回の場合だと、娯楽に費やせる時間は有限であることからTV視聴時間が長いとゲーム利用時間が短くなる仮説が考えられ、 TVwatch_day(1日当たりの平均TV視聴時間) がCM接触効果の交絡因子になっている可能性があります。
先ほどのグラフからCM接触あり(介入群)にTV視聴時間が長いユーザーが多いため、CM接触なし(対照群)と比べてゲームに時間を割けるユーザーが少なく、ABテストでCM接触の効果を測る場合は過小評価している可能性を考慮する必要があるかもしれません。
まとめ&注意点
今回は介入群と対照群でデータ分布が異なる変数をAdversarial Validationの考えを用いて推定できるか実験してみました。
注意点としては、タイトルに「セレクションバイアスの発生箇所を推定する」と書いたものの、そもそも分布が異なる変数が存在してもその変数が交絡因子である確証がないことや、交絡因子となる変数がデータセットに含まれていない場合は推定できません。またGBDTの特徴量重要度の妥当性の話や、上手くいくかはデータによりけりだと思われる部分も注意点だと思います。
よって、結果を鵜呑みにせず「該当する変数が存在した場合、その変数が交絡因子であれば過大(もしくは過小)評価している可能性があるので注意する必要があるかも」くらいの補助的な使い方がよさそうです。
思いつきで個人的興味で試してみましたが面白かったです。
感想や「ここ間違ってるよ!」等のコメントはいつでもお待ちしています。
参考文献
効果検証入門〜正しい比較のための因果推論/計量経済学の基礎
岩波データサイエンス Vol.3(岩波書店)
「交絡因子」は,なぜ「セレクションバイアス」を引き起こすか.
コンセプトドリフト対処のための,Adversarial Validation を⽤いた学習データ選択に関する考察