はじめに
ビジネスの場において,施策介入の効果の検証は,必要とされる分析技術の一つです.
介入効果の検証は,RCT(Randomized Control Trial)と呼ばれる無作為化比較が基本ですが,「交絡因子」と呼ばれる”比較対象群の特定変数の偏り”が存在すると,「セレクションバイアス」と呼ばれる”介入効果の推定精度の低下”が発生することが知られています.
しかし,昨今の文献では,両者の概念の個別の説明は多々見られるものの,その関係性をより詳細に言語化したものが少ないように思います.
そこで,本ブログでは,効果検証の基本要素とメール配信を例にした実践解析を基に,「交絡因子」の偏りが「セレクションバイアス」を発生させる理由についての言語化を行います.
言語化の結論はこちらです.
""交絡因子の偏りにより発生する,観測結果への不均一な重み付けが,比較集団における母平均への推定誤差を引き起こす""
目次
- はじめに
- 介入効果を測る基本姿勢:「ポテンシャルアウトカムフレームワーク」と「平均処置効果」
- セレクションバイアスの数学的定義
- 交絡因子によるセレクションバイアスの発生
- 「交絡因子」は,なぜ「セレクションバイアス」を引き起こすか
- まとめ
- 追記
- 付録:シンプソンのパラドックス
- 参考文献
本ブログで目標とする,「介入効果の推定精度の低下」の説明には,そもそも「介入効果とは?」という定義が必要です.
そこで,本章では,メール配信を例にとり,介入効果を測る基本姿勢である「ポテンシャルアウトカムフレームワーク(Potential Outcome Framework)」と介入の実質的定義である「平均処置効果(Average Treatment Effect)」について述べます.
(メール配信の問題設定)
あるユーザー i に対して,メール配信あり(Zi=1)およびメール配信なし(Zi=0)の両者の介入を行い,その時の各売り上げ,Yi = {Yi(1)(Zi=1), Yi(0)(Zi=0)} を評価する.
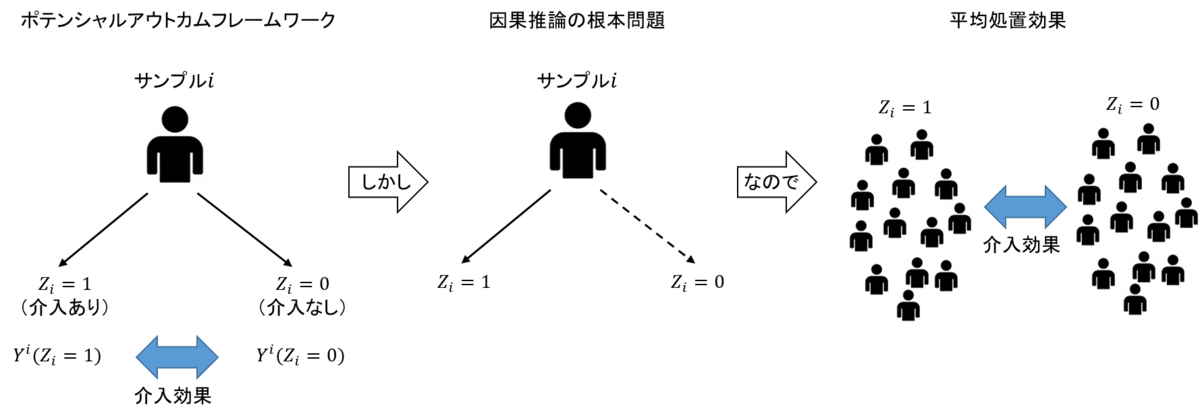
このように,あるサンプル i に対して,介入された場合の観測結果Yi(1)と介入されなかった場合の観測結果Yi(0)があると考え,その差に本当の介入の効果があるとする考えを,「ポテンシャルフレームワーク(Potential Outcome Framework)」と呼びます.
しかし,ユーザー i という一人の対象では,介入あり,もしくは,介入なしのどちらか片方の状態しか取り柄ません.このような,介入の有無のどちらかの選択により,もう片方の状態が観測できなくなることを「因果推論の根本問題」と呼びます.
介入の有無がどちらかしか選択できない以上,単一のユーザーで介入の効果を推定することは不可能です.そこで,複数ユーザーによる母集団を考え,観測結果の期待値を評価します.この場合,メール配信の効果は,「メールを配信するときの売り上げの期待値:E[Y(1)]」と「メールを配信しないときの売り上げの期待値:E[Y(0)]」の差にて表現され,この母集団における平均的な効果は「平均処置効果(Average Treatment Effect:以下ATE)」と呼ばれます.
$\gamma = E[Y^{(1)}]-E[Y^{(0)}]$
また,現実問題として,異なる2つの同質な標本集団から,ATEを推定することを考慮した場合,以下のように記述できます.
$\gamma_{native} = E[Y^{(1)}|Z=1] - E[Y^{(0)}|Z=0]$
”””ユーザー集団により測定した観測値の期待値の差を持って,介入の効果とする.”””
これが,介入効果を測る基本姿勢です.
図:介入効果を測る基本姿勢 ## セレクションバイアスの数学的定義介入効果の定義は,「ユーザー集団により測定した観測値の期待値の差」であることを前章にて確認しました.では,上記ATEの定義を用いて,”介入効果の推定精度の低下”である「セレクションバイアス」とは何か?について考えます.
上記ATEを展開すると,
$\gamma_{native} = E[Y^{(1)}|Z=1] - E[Y^{(0)}|Z=0]$
$= E[Y^{(1)}|Z=1] - E[Y^{(0)}|Z=1] + E[Y^{(0)}|Z=1] - E[Y^{(0)}|Z=0]$
$= E[Y^{(1)}-Y^{(0)}|Z=1] + E[Y^{(0)}|Z=1] - E[Y^{(0)}|Z=0]$
このように,$\gamma_{native}$は,「Z=1の集団における,各介入{0,1}における観測値の差の期待値」である$E[Y^{(1)}-Y^{(0)}|Z=1]$と,「Z=0 Z=1の各集団における介入のない場合の観測期待値の差」である$E[Y^{(0)}|Z=1] - E[Y^{(0)}|Z=0]$にて表現されます.
この時,Zの選択に依らず,観測値の差の期待値が一定の場合,つまり,
$E[Y^{(1)}-Y^{(0)}|Z=1] = E[Y^{(1)}-Y^{(0)}]$
「Z=0 Z=1の各集団における介入のない場合の観測期待値の差」である$E[Y^{(0)}|Z=1] - E[Y^{(0)}|Z=0]$がゼロ以外の値を取るとき,
介入効果の推定量は,「母集団の介入効果から外れた値」になることが分かります.
前章では,介入効果を比較するべき2つの集団おいて生じる,介入とは無関係な観測値の有意な差:$E[Y^{(0)}|Z=1] - E[Y^{(0)}|Z=0]$がセレクションバイアスの正体であることを述べました.
では,何かこの偏りを発生させているのか?
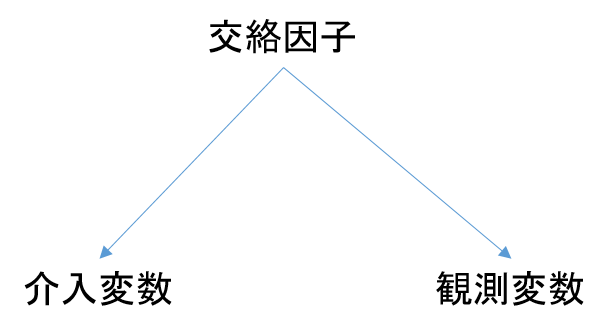
結論からの述べると,それは「交絡因子」という介入変数と観測変数の双方に相関を持つ因子の存在です(図:グラフによる表現).
交絡因子が比較対象群の中で偏って分布していると,介入とは無関係な観測値の差が生じます.
図:グラフ表現による表現
本章では,「交絡因子の偏り」と「セレクションバイアスの発生」の依存関係を確認するため,下記表にて記載されるメール配信の結果を用いた介入効果の推定を行います.
(メール配信の問題設定)
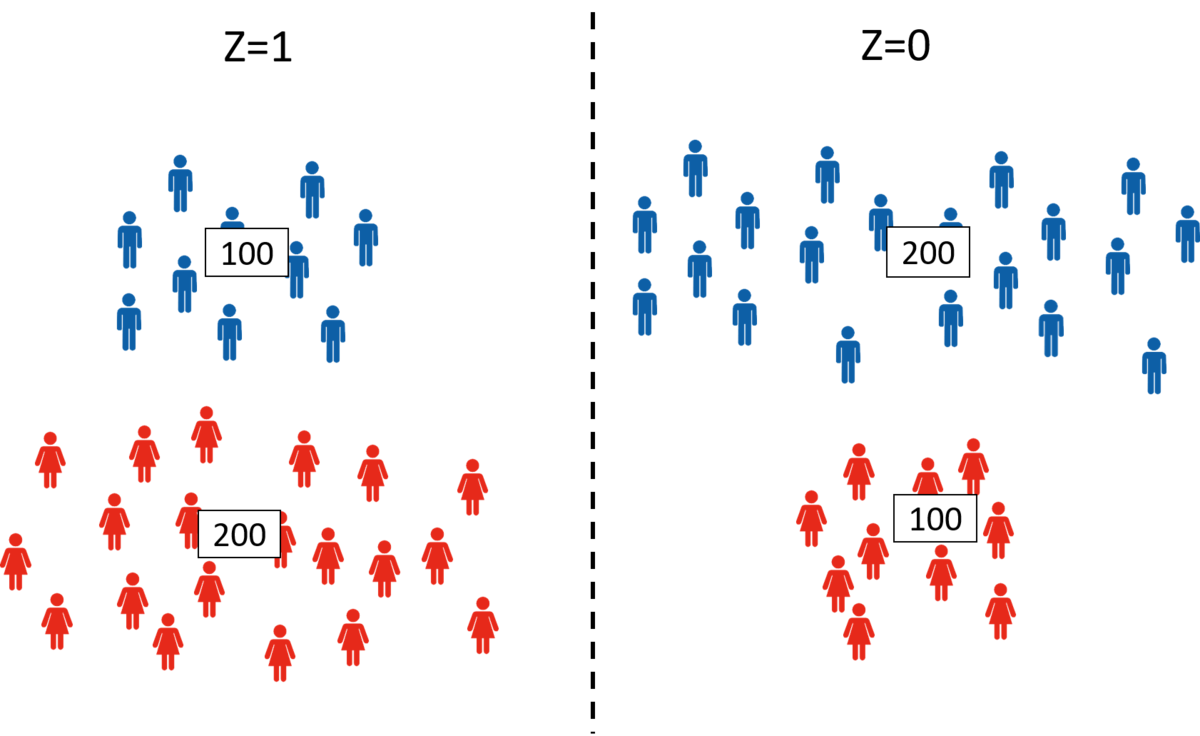
男性300人女性300人の集団から,介入あり(Z=1)介入なし(Z=0)の2集団を作成し,介入効果(メール配信)の測定を行う(図:標本集団).しかし,RCTのような均一な分布ではなく,Z=1(男100:女200) Z=0(男200:女100)のような共変量(性別)の割合が異なるデータ配分を行う.また,女性の場合,介入の有無に依らず,観測値(売り上げ:Y)が男性より500円高い場合を考える.
つまり,介入変数(Z)と観測変数(Y)が,説明変量(X:性別)(=交絡因子)により変化する系において,その変数の偏ったデータ集団を作った場合の介入を評価する.
この場合に,メールの効果を単純な一人当たりの売り上げの差だと考えると,Y1とY0の平均を計算して,
$Y^{(0)}の平均 : (2000 × 200 + 2500 × 100) ÷ 300 = 2166.6666...$
$Y^{(1)}の平均 : (2500 × 100 + 3000 × 200) ÷ 300 = 2833.3333...$
となり,$Y^{(1)} - Y^{(0)} = 2833 - 2166 = 666$と, 男女の持つ本来の介入効果(500円)より高い値が推定されます.
一方で,男女は均一に分布している(=交絡因子による偏りなし)の場合は,
$Y^{(0)}の平均 : (2000 × 150 + 2500 × 150) ÷ 300 = 2250$
$Y^{(1)}の平均 : (2500 × 150 + 3000 × 150) ÷ 300 = 2750$
となり,$Y^{(1)} - Y^{(0)} = 2750- 2250 = 500$と,男女の持つ本来の介入効果と一致します.
つまり,”””交絡因子(性別)の偏りにより,比較データ群における観測変数の平均値に誤差が生じる””””
これが,「交絡因子」とセレクションバイアスの依存関係です.
介入変数(Z)と観測変数(Y)にともに相関を持つ「交絡因子」が,偏った比較データ群を効果検証に用いる場合,観測変数の平均値に誤差が生じることが分かりました.
ではそもそも,「交絡因子」の偏りが,なぜ,観測変数の平均値に誤差を引き起こすのでしょうか.
前章のY1とY0の平均値の算出に着目すると,最大観測値であるY1(女性:3000円)と最小観測値であるY0(男性:2000円)に,ともに最大人数200人が重みづけされていることが分かります.
重み付け係数が大きいということは,平均値に対する観測値の寄与が大きくなることを意味しており,
本解析の場合には,
介入ありデータにおいて,最大観測値3000円の寄与が最も大きくなるような平均の算出が,また,
介入なしデータにおいては,最小観測値2000円の寄与が最も大きくなるような平均の算出が行われていています.
その結果,観測変数の平均値に,過剰な差が生じていると考えられます(図:重み付けの違いによる平均値の変化)
 図:重み付けの違いによる平均値の変化また,この重み付け係数は,比較データ群における性別の配分割合,つまり,「交絡因子(性別)の偏り」により発生しています.
ここから,””””交絡因子の偏りにより発生する,観測結果への不均一な重み付けが,比較集団における母平均への推定誤差を引き起こす””””ことが分かり,これが,「交絡因子」が「セレクションバイアス」を引き起こす理由であるとわかります.
まとめ
効果検証の基本要素とメール配信を例にした実践解析を基に,「交絡因子」の偏りが「セレクションバイアス」を発生させる理由についての考察を行いました.
その結果,
“““交絡因子の偏りにより発生する,観測結果への不均一な重み付けが,比較集団における母平均への推定誤差を引き起こす””””ことが分かりました.
本内容は,因果推論の中では基礎中の基礎に当たる部分であり,実現場での解析においては,さらに高度な知識と技術が求められることは当然だと考えております.
しかし,「交絡因子」「セレクションバイアス」のような基礎概念の理解を怠ると,積み重ねた理論の崩壊を招く場合があると考え,今回はこのようなトピックをレポート化しました.
間違い等ありましたら,コメント・修正いただけると幸いです.
以上です.
## 追記:セレクションバイアスの生じる別のパターン※本追記は,同じ所属企業のメンバーから頂いたコメントをもとに作成しております.
コメントいつも感謝します.
本内容では,セレクションバイアスの生じるシチュエーションとして,「Zの選択に依らず,観測値の差の期待値が一定」である状況を仮定し,
$E[Y^{(1)} - E[Y^{(0)}]|Z=1] = E[Y^{(1)} - E[Y^{(0)}]]$としています.
しかし,本例題における「男性の$Y^{(0)}$」を2000円→2500円にし,介入効果のある女性を多く選択するなど,
「介入効果が大きそうな人を介入群に配置する」行為を行うと,ATT > ATEとなり,平均の差は余計に多く見積もられます.
つまり,
$E[Y^{(1)} - E[Y^{(0)}|Z=1] > E[Y^{(1)} - Y^{(0)}]$ならば,
$\gamma_{native} = E[Y^{(1)}-Y^{(0)}|Z=1] + (E[Y^{(0)}|Z=1] - E[Y^{(0)}|Z=0])$
$> E[Y^{(1)}-Y^{(0)}] + (E[Y^{(0)}|Z=1] - E[Y^{(0)}|Z=0])$
$> E[Y^{(1)}-Y^{(0)}]$
(本編:セレクションバイアスの数学的定理より)
本レポートでは,「交絡因子によるセレクションバイアスの発生」の章において,「男女それぞれの介入効果は500円なのに全体平均を取ると約600円もの効果が出ている」という魔法のような現象を見ました.
本レポートではこれを「セレクションバイアス」という一言で片づけましたが,本現象は,統計学の中における「シンプソンのパラドックス」という重要な位置づけを持ちます.
データのみから結論を導く従来の統計学では,本現象を「介入変数が説明変数に影響を与えたのでは?」と考え,性別と観測変数の因果を結論づけることができません.したがってシンプソンのパラドックスは発生しません.このように,従来の標準統計学で用いられる数学では,「性別と観測値」の間の因果を記述することができないのです.
しかし,グラフモデルに代表される今日注目の統計的因果推論の体系は,因果を数学的記述を提供します.
シンプソンのパラドックスは,このような因果推論発展前後の統計学の状態を説明する歴史的な現象なのだと思います.
## 参考文献 本ブログを作成するにあたり,下記文献を参照いたしました.
[1]効果検証入門 安井翔太(著)+株式会社ホクソエム(監修)技術評論社
[2]入門統計的因果推論 Judea Pearl et.al.
[3]https://qiita.com/usaito/items/f713d93732db82696a76「傾向スコアでセレクションバイアスを補正する」
[4]https://healthpolicyhealthecon.com/2014/11/30/rubin_causal_model/#:~:text=%EF%BC%88%E6%AD%A3%E7%A2%BA%E3%81%AB%E3%81%AF2%E3%81%A4%E3%81%AE,Factual%E3%81%A8%E5%91%BC%E3%81%B0%E3%82%8C%E3%81%BE%E3%81%99%EF%BC%89%E3%80%82「統計学における因果推論(ルービンの因果モデル)」