はじめに
前回、『Uplift-Modelingで介入効果を最適化する』ではRCTによって得られたデータからある介入の効果を平均的に求めるのではなくて、ある特徴量を持った集団にのみ介入するという戦略を試しました。その結果、「男性向け」・「女性向け」プロモーションメールを平均的によかった方に全振りするのではなくて、約65%の人には「男性向け」メール、残りの人には「女性向け」メールを送る戦略がコンバージョンを最大化することを示しました。
しかし、いつでもRCTを行えるわけではありません。例えば、あるコンビニのキャンペーンでおにぎり全品100円セールとおでん全品70円セールを定期的に開催していたとします。しかし、これらのキャンペーンの効果は店舗ごとに異なると考えられる(学生が多く住む地域ではおにぎりのキャンペーンが、年齢層が高い地域ではおでんのキャンペーンが有効など、同じ店舗でも季節により介入効果の大きさが違うと思われる)ためUplift Modlingを用いてどの店舗でどちらのキャンペーンを重点的に行うかを決めたいとします。しかし、これまで蓄積されているデータはRCTではなく、ある時期に全店舗に同じキャンペーンを打ったというような観察データであると考えられます。(これから大規模にRCTをすることも不可能ではないかもしれませんが、すでに蓄積されている手元のデータから示唆を出せるほうがこの場合対費用効果があると思われます。)今回は、このような状況においてRCTとは言えない観察データを用いたUplift Modelingで介入効果を最大化することを目指します。
*本記事で使用したコードはこちら (adj-uplift-modeling1.ipynb) からご覧いただけます。
目次
観察データにおけるUplift Modelingの問題点
RCTによって得られたデータではなくて、観察データを用いることの問題点は交絡因子の存在です。例えば、先ほどのコンビニにおけるキャンペーンの例において、季節周期的にキャンペーンが打たれていたデータをRCTにより得られたデータと誤解してUplift Modelingをそのまま当てはめると問題が起こると考えられます。なぜなら、季節がキャンペーンの割り当て確率とアウトカムである店舗の売り上げの両方に影響を与えるため、あるキャンペーンが売り上げ向上に寄与したのか、それが打たれた時期が売り上げ向上に寄与したのかわからないためです。
このような場合、観察データから$ATE$ すなわち介入の母集団における平均的な因果効果を推定する方法として、傾向スコアを用いる方法があります。これは、拙著記事『傾向スコアでセレクションバイアスを補正する』で紹介しました。しかし、この記事で用いた方法では、全店舗についての平均的な因果効果を推定するにとどまります。すなわち、おにぎり全品100円セールとおでん全品70円セールのどちらが平均的に良さそうか( $ATE = E(Y_1 - Y_0)$ )を推定するにとどまります。しかし、今回は各店舗ごとにどちらのキャンペーンがどれくらい良さそうかを予測することで売り上げアップにつなげたいと考えているため、興味があるのはあるコンビニ $i$ についての条件付き期待値である個人介入効果 $ITE,(,Individual,Treatment,Effect,)$ ( $ITE_i = E(Y_{1 i}- Y_{0i} ,|, X_i)$)です。( $X_i$ はコンビニ $i$ の特徴量)
観察データにおけるUplift Modelingの手法[1]
ここでは、引用論文で紹介されている手法のうち、**The Transformed Outcom Tree Method (TOT)**について紹介します。
以下では、ある個人を$i$, その個人が持つ特徴ベクトルを$X_i$, 介入の有無を $W_i (binary)$, $W_i = 1$の時のアウトカムを$Y_i(1)$、$W_i = 0$の時のアウトカムを$Y_i(0)$として論文に表記を合わせます。この時、観測されるアウトカムは、
Y_i^{obs} = W_iY_i(1) - (1 - W_i)Y_i(0)
と表せます。また興味がある $ITE,(,Individual,Treatment,Effect,)$ (または、$CATE,(,Conditional , Average , Treatment,Effect,)$)は、以下のように表せます。
ITE_i = \tau(X_i) = E[Y_i(1) \,|\, X_i] - E[Y_i(0) \,|\, X_i]
ちなみに、傾向スコアを用いた分析で推定した$ATE,(,Average,Treatment,Effect,)$は、
\begin{align}
ATE\\
&= E[\tau(X_i)]\\
&= E[E[Y_i(1) \,|\, X_i] - E[Y_i(0) \,|\, X_i]] \\
&= E[Y_i(1)] - E[Y_i(0)]
\end{align}
つまり、$ITE_i$の期待値でした。また、傾向スコア $e(X_i)$は、
e(X_i) = P(W_i = 1 \,|\, X_i)
とします。このとき、ある仮定*のもとで以下の推定量 $Y_i^{TOT}$ が $\tau(X_i)$の不偏かつ一致推定量となることが示されます。つまり、
\begin{align}
Y_i^{TOT}
&= Y_i^{obs} \cdot \frac{W_i - e(X_i)}{e(X_i) \cdot (1 - e(X_{i}))}\\
&= Y_i(1) \cdot \frac{X_i}{e(X_i)} - Y_i(0) \cdot \frac{1 - W_i}{1 - e(X_i)}\\
\\
Then,\\
&E[Y_i^{TOT} \,|\, X_i] = \tau{(X_i)}
\end{align}
です。よって、観察データにおけるUplift Modelingでは、アウトカム $Y_i$ を傾向スコア $e(X_i)$ を用いて、$Y_i^{TOT}$ へと変換することでUplift Scoreを求めると観察データの問題点である交絡因子の影響を補正できるということになります。以下ではこの手法を傾向スコアの回で使用したスマホアプリCMのデータを用いて試してみます。
*ここで紹介した、不偏性や一致性は $CIA (Conditional,Independence,Assumption)$という仮定のもとで導かれます。これは、『傾向スコアでセレクションバイアスを補正する』で出てきた仮定である「強い意味での無視可能性」と実は同じ仮定で、$CIA : (Y_i(0), Y_i(1)) \perp z_i,|,x_i$ が成り立っていることを要求します。
利用データについて
今回は、テレビCMがあるスマホアプリの利用率や利用回数、利用時間に与える効果を傾向スコアを用いてアウトカムを補正した上で、Uplift Modelingにより最大化することを目指します。データセットはこちらを利用させていただきました。
ちなみに、テレビCM視聴はアプリ利用率を平均3.2%、アプリ利用時間を平均5.3回、アプリ利用時間を平均1513秒、平均的に押し上げることを『傾向スコアでセレクションバイアスを補正する』では推定しました。
また今回は、よりシンプルな介入戦略を立てるために説明変数として、子供の有無ダミー、居住地ダミー(関東・東海・京阪神・京浜)、年齢と性別の組み合わせダミー(T層:13~19歳の男女、F1層:20~34歳の女性、F2層:35~49歳の女性、F3層:50歳以上の男性、M1層:20~34歳の男性、M2層:35~49歳の男性、M3層:50歳以上の男性)を用いることとします。
回帰問題への応用
ここでは、スマホアプリのテレビCMをある層に絞って視聴してもらうことで、アプリ利用時間を効率化できることを示します。アプリ利用率をアウトカムにとっても良かったのですが、傾向スコアによる補正を行うと連続変数となり、回帰問題となってしまうことからこれで正しいのか不安になったため、おまけとして別記事にまとめようと思います。
また、傾向スコアによる補正が有効に働くことを確認するため傾向スコアによる補正をせず、2つの学習器を用いたSeparate Model Approachと傾向スコアを用いたThe Transformed Outcome Methodによる結果を比較します。そして、最後にUplift Scoreを説明変数で回帰することにより、どの属性がCM視聴のアプリ利用時間に対する効果を左右しているかを分析します。
ちなみに、先ほど紹介しましたが、TOTでは、目的変数を変換することによりUpliftの推定量を直接予測しにいきます。よって、比較対象である、Separate Model Approachとは異なり、学習器の予測精度の良さがUplift Modelingの良さに直結すると考えられます。逆にいうと、学習器の予測精度がある程度保証されないと、ここでのUplift Modelingによる介入戦略は信頼のおけないものになり得るということです。この点を鑑みて、TOTを用いたパートでは、学習器に精度が比較的良いと考えられるランダムフォレスト回帰を用いています。
Separate Model Approach
# データの読み込み
data_df = pd.read_csv('https://github.com/iwanami-datascience/vol3/raw/master/kato%26hoshino/q_data_x.csv')
data_df.head()
# 説明変数と目的変数を指定
cols = ["child_dummy", "area_kanto", "area_tokai", "area_keihanshin",
"T", "F1", "F2", "F3", "M1", "M2"]
X = data_df[cols]
y = DataFrame(data_df.gamesecond)
# CMありをtreatment, CMなしをcontrolとする
treat = (data_df.cm_dummy == 1).tolist()
# train, test半分ずつに分ける
y_train, y_test, train_treat, test_treat, X_train, X_test = train_test_split(y.values, treat, X, test_size=0.5, random_state=2)
# indexをリセット
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
# Separate Model Approach
# 学習用に用いるデータを生成
num = len(y_train)
treat_y = np.reshape(np.array([y_train[i] for i in range(num) if train_treat[i] is True]), -1)
control_y = np.reshape(np.array([y_test[i] for i in range(num) if train_treat[i] is False]), -1)
treat_X = DataFrame([X_train.loc[i] for i in range(num) if train_treat[i] is True])
control_X = DataFrame([X_train.loc[i] for i in range(num) if train_treat[i] is False])
# ランダムフォレスト回帰を用いる
params_rf = {"max_depth": [10, 50, 100, 200, 500]}
gs_rf_treat = GridSearchCV(RandomForestRegressor(n_estimators=500),
param_grid=params_rf, cv=5)
gs_rf_control = GridSearchCV(RandomForestRegressor(n_estimators=500),
param_grid=params_rf, cv=5)
# 介入群と非介入群それぞれでパラメータチューニング及びスマホアプリ利用時間を予測するモデルを構築
gs_rf_treat.fit(treat_X, treat_y)
gs_rf_control.fit(control_X, control_y)
# uplift-scoreの算出
# CMを見た場合のアプリ利用時間
pred_treat = gs_rf_treat.predict(X_test)
# CMを見なかった場合のアプリ利用時間
pred_control = gs_rf_control.predict(X_test)
# 今回は、(CMを見た場合のアプリ利用時間) - (CMを見なかった場合のアプリ利用時間) をuplift_scoreとする。
uplift_score = pred_treat - pred_control
ここで結果を描画してみます。AUUCというのは今の所メジャーなupliftの評価指標で、uplift(青線)とbaseline(黄線)の間の面積で計算されます。
uplift(青線)は、横軸で表されるUplift Score Rank以上の人のみに介入した時に、全く介入しなかった場合に比べてどれだけアプリ利用時間が増えるかを表しています。baselineは横軸で表されるUplift Score Rank以上の人にランダムに介入した時のupliftを表しています。
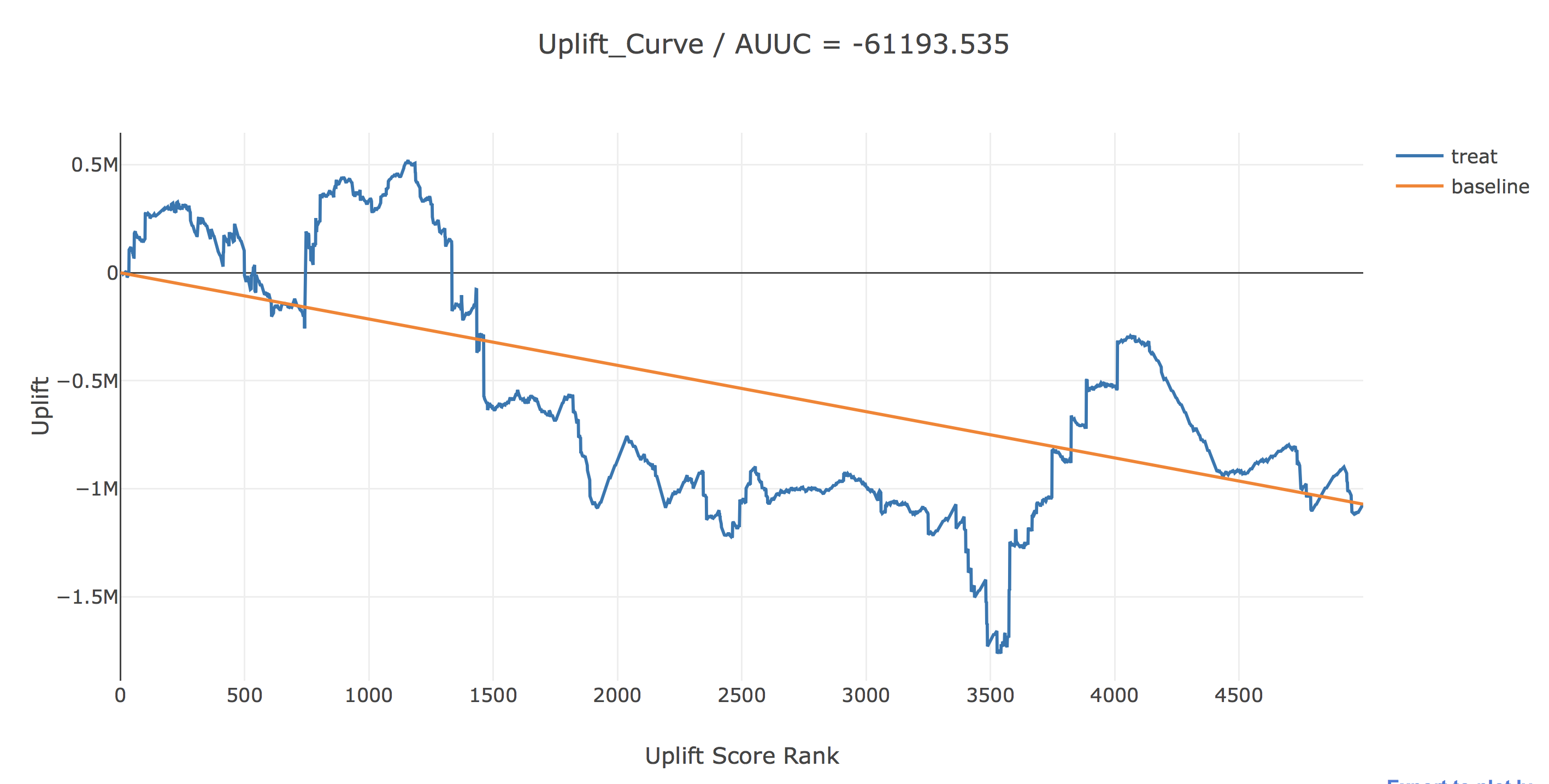
これを見るとUplift Scoreが上位1150人くらいにのみ介入することで最大合計で約52万秒のUplift(介入郡内平均約452秒)が見込めます。しかし、AUUCはマイナスの値となっていたり、途中で青い線が上下にギザギザした形になっていることからうまくUplift Scoreによるランクづけができていない結果となっています。これは、CMの視聴確率とアウトカムの両方に影響を与える説明変数のCM視聴による因果効果の大小に対する影響を誤って評価してしまっていることに起因すると考えられます。(これがどの説明変数であるかは後ほど分析します。)
また、uplift scoreを説明変数で回帰することにより、どの説明変数が介入効果を押し上げているかについて簡単に分析してみます。
### 正則化項なしの線形回帰
lr = LinearRegression()
lr.fit(X_test, uplift_score)
for feature, coef in zip(X_train.columns, lr.coef_):
print(f"{feature} / {round(coef, 4)}")
### これについては傾向スコアで補正した後の結果と比較
------------
child_dummy / 908.637
area_kanto / -1496.5464
area_tokai / -3011.7085
area_keihanshin / 709.94
T / 12162.6652
F1 / 1303.4776
F2 / 1837.2586
F3 / 933.6289
M1 / 2602.7832
M2 / 3538.0977
------------
The Transformed Outcome Method
次にアウトカムを傾向スコアを用いて補正することで個人介入効果の推定値に対して直接モデリングしてみます。
# データの読み込み
data_df = pd.read_csv('https://github.com/iwanami-datascience/vol3/raw/master/kato%26hoshino/q_data_x.csv')
data_df.head()
# 傾向スコアを求める
# 説明変数
cols_ = ["age", "sex", "TVwatch_day", "marry_dummy", "child_dummy", "inc", "pmoney",
"area_kanto", "area_tokai", "area_keihanshin",
"job_dummy1", "job_dummy2", "job_dummy3", "job_dummy4", "job_dummy5", "job_dummy6",
"fam_str_dummy1", "fam_str_dummy2", "fam_str_dummy3", "fam_str_dummy4"]
X_ = data_df[cols_].copy()
# 切片の導入
X_.loc[:, "Intercept"] = 1
# CM視聴有無ダミー
z1 = data_df.cm_dummy
# StatsModelsのLogitにより傾向スコアを推定
glm = sm.Logit(z1, X_)
result = glm.fit()
ps = result.predict(X_)
ps
------------
0 0.046217
1 0.255983
2 0.177427
3 0.227593
4 0.242373
------------
# Propensity Scoreで補正された目的変数のカラムを作成
data_df.loc[:, "ps"] = ps
data_df.loc[:, "adj_gamesecond"] = 0
data_df.loc[data_df.cm_dummy == 1, "adj_gamesecond"] = data_df.loc[data_df.cm_dummy == 1, "gamesecond"] / data_df.loc[data_df.cm_dummy == 1, "ps"]
data_df.loc[data_df.cm_dummy == 0, "adj_gamesecond"] = -data_df.loc[data_df.cm_dummy == 0, "gamesecond"] / (1 - data_df.loc[data_df.cm_dummy == 0, "ps"])
adj_y = data_df[["gamesecond", "adj_gamesecond"]]
# CMありをtreatment, CMなしをcontrolとする
treat = (data_df.cm_dummy == 1).tolist()
# train, test半分ずつに分ける
adj_y_train, adj_y_test, train_treat, test_treat, X_train, X_test = train_test_split(adj_y, treat, X, test_size=0.5, random_state=2)
# indexをリセット
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
adj_y_train = adj_y_train.reset_index(drop=True)
adj_y_test = adj_y_test.reset_index(drop=True)
# ランダムフォレスト回帰を用いる
params_rf = {"max_depth": [10, 50, 100, 200, 500]}
gs_rf = GridSearchCV(RandomForestRegressor(n_estimators=500), param_grid=params_rf, cv=5)
# パラメータチューニング及び補正スマホアプリ利用時間を予測するモデルを構築
gs_rf.fit(X_train, adj_y_train.adj_gamesecond)
# 補正uplift_scoreを求める
adj_uplift_score = gs_rf.predict(X_test)
ここでも先ほどと同じように、uplift(青線)は、横軸で表されるAdj-Uplift Score Rank以上の人のみに介入した時に、全く介入しなかった場合に比べてどれだけアプリ利用時間が増えるかを表しています。baselineは横軸で表されるAdj-Uplift Score Rank以上の人にランダムに介入した時のupliftを表しています。
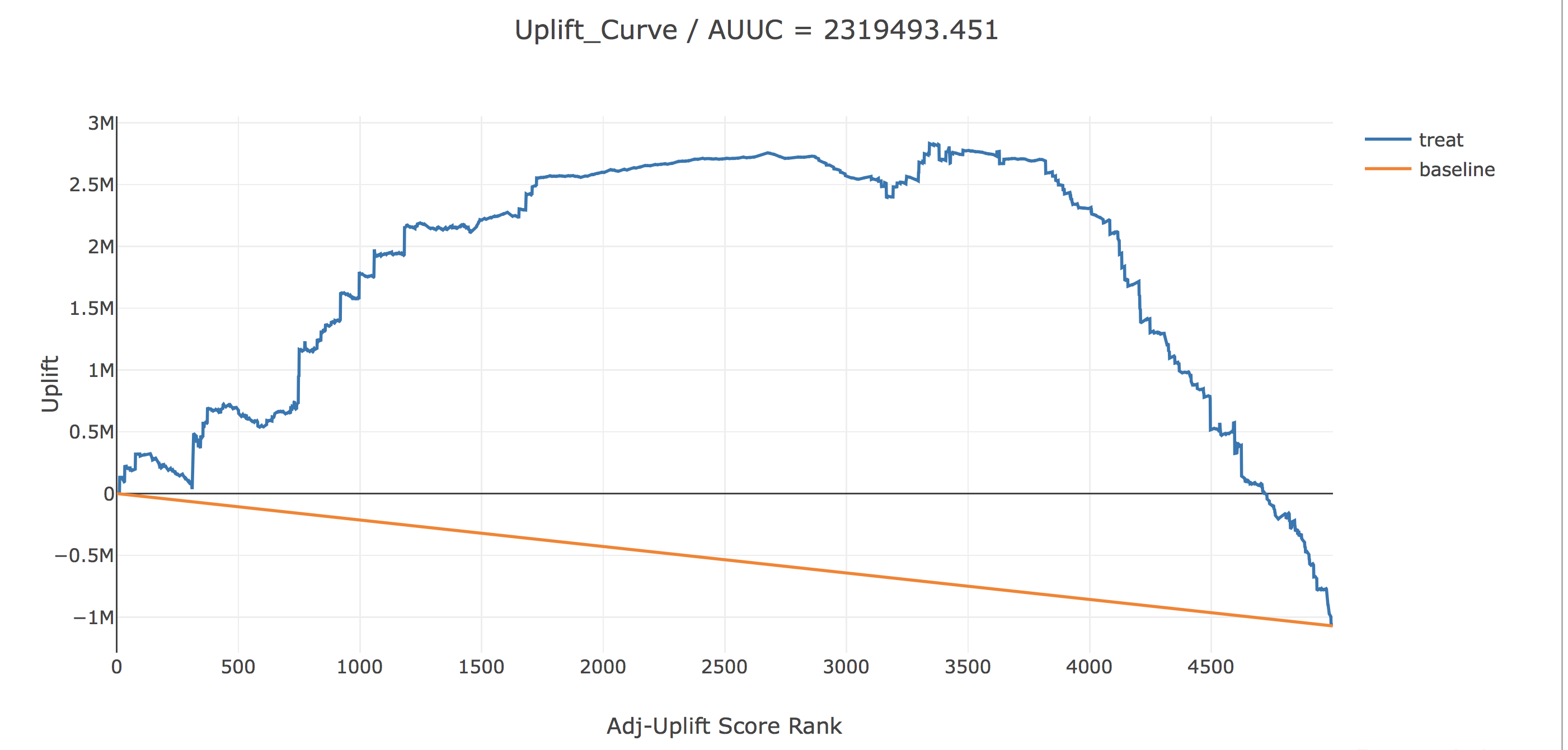
これを見ると大きく様子が変わっていますね。AUUCも大きな正の値となっています。また、Uplfit Scoreが上位約3350人にのみ介入することで、最大合計で282万秒(介入郡内平均833秒)のUpliftが見込まれます。さらにここでは、横軸にAdj-Uplift Scoreをとって描画してみます。
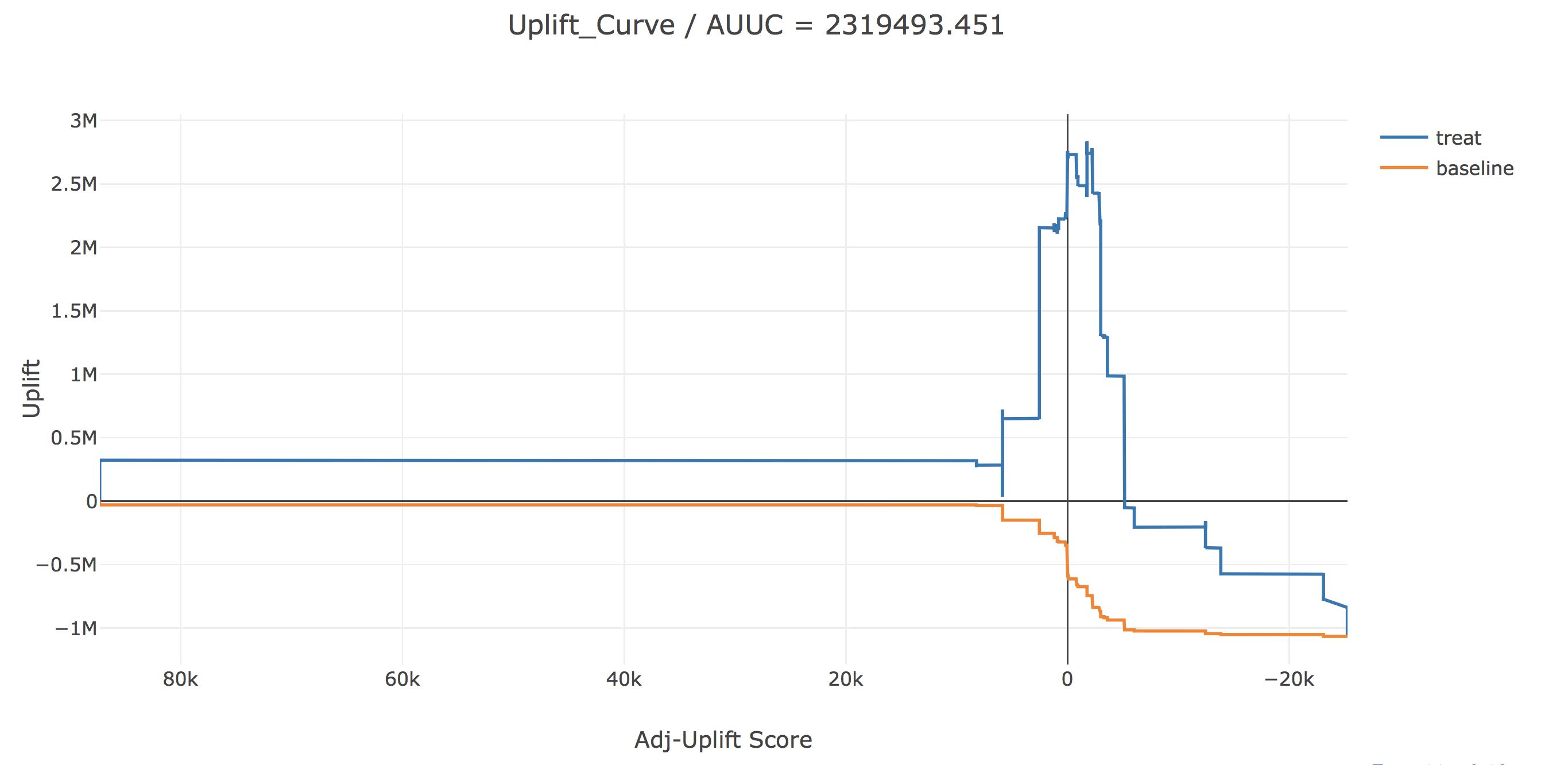
こちらをみて見ると、Adj-Uplift Scoreすなわち、個人介入効果の予測値がおおよそ0以上と予測された人に介入するときにUpliftが最大化されるという直感に整合的な結果となっています。
さらに、先ほどと同じようにAdj-Uplift Scoreを説明変数に回帰することで、どの説明変数が介入効果を押し上げているかについて今一度分析してみます。
lr = LinearRegression()
lr.fit(X_train, gs_rf.predict(X_train))
for feature, coef in zip(X_train.columns, lr.coef_):
print(f"{feature} / {round(coef, 4)}")
------------
child_dummy / -7569.4138
area_kanto / -2628.5153
area_tokai / -4392.3121
area_keihanshin / 11195.8322
T / 4560.244
F1 / 368.2905
F2 / 2996.2029
F3 / -593.36
M1 / -5643.6574
M2 / 11198.8379
------------
先ほどの分析と比較して興味深いのは、「子供有無ダミー」でしょう。傾向スコアによる補正前は子供がいるとCM視聴による因果効果を増やすと推定されていましたが、傾向スコアによる補正後は大きな負の値が推定されています。すなわち、子供がいるとCM視聴による因果効果が減るというのです。
実は傾向スコアを推定した際のロジスティック回帰モデルの変数をみて見ると「子供有無ダミー」の係数は有意に正の値が推定されていました。つまり、子供がいるとCMを視聴しやすくなるということです。またもちろん、CM視聴は多かれ少なかれアプリ利用時間に正の影響を与えると考えられます。しかし、子供がいると育児等々でCMを視聴したことによるアプリ利用時間の増加分が減少することも可能性としてはあり得ないことではありません。傾向スコアを用いて補正しない場合は、子供がいるとCM視聴確率が増えるということを考慮しないため、因果効果の増分が、子供がいることによるCM視聴割合の増加なのか、子供がいることそれ自体なのかを分けないで考えてしまい子供の有無が因果効果に正の影響を与えるという誤った推定をしてしまったのだと思われます。
さいごに
今回は、RCTとは言えない観察データについて傾向スコアによる補正を用いてUplift Modelingをすることにより、介入戦略を正しく効率化できることを示しました。また、傾向スコアを用いないと、介入割り当て確率とアウトカムの両方に影響を与える特徴量(今回は子供有無ダミー)が介入の因果効果に与える影響を誤って推定してしまうことが、うまくUplift Modelingできない要因の一つだと考えられることも見てきました。
今後は、今回扱わなかった2値変数がアウトカムの場合の傾向スコアによる補正がうまくいくのかどうかを試してみたり、決定木を用いたUplift Modeling手法を実装していけたらいいなと思っています。
参考
[1] Athey, S and Imbens, G. Machine Learning Method for estimating heterogeneous causal effects. stat, 1050:5, 2015
[2] Gutierrez, P and Gerardy, J, Y. Causal Inference and Uplift Modeling A review of the literature. JMRL: Workshop and Conference Proceedings 67:1-13, 2016