勾配法とは
雑把に勾配法とは、
「求めたい未知の関数を繰り返し微分することで、その傾きが0に近い点、つまり最小値・最大値(時に極大・極小に落ち着きますが…)を探し出す方法である。」
です。
これだけ言われても「だから何?」と言われそうですが…
これの何が嬉しいかと言うと、解析的に微分が難しいものや、多くのデータのプロットから尤もらしい関数を作り出すことができることにあります。
回帰分析
勾配法を用いることで多くのデータから尤もらしい関数を導き出すことができます。
具体例を用いてみましょう。
$i$番目に$x_i, y_i$をもつ50個のデータがあったとすると、
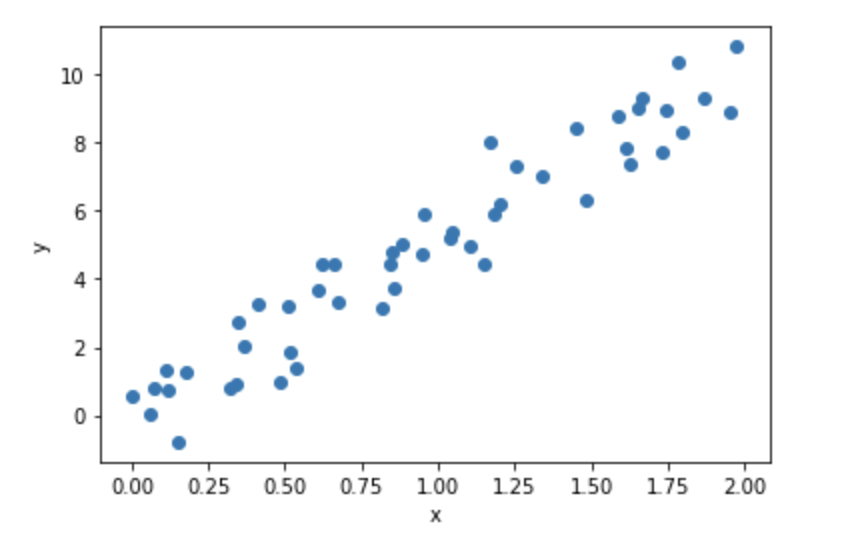
このようにプロットすることができます。
「真ん中にそれっぽい直線を引いてください!」と言われたら

ほとんどの人がこのような直線を引くのではないでしょうか?
要は、この直線を求めることを回帰分析と読んでいるだけです。
ちなみに、この関数のように変数が1つの時の回帰分析を特に単回帰分析と言います。
次に、回帰分析をするために必要な手法の1つである最小二乗法を説明します。
最小二乗法
複数のデータから尤もらしい関数を作り出すためには以下の4ステップを踏みます。
- 適当な関数を作っておく。
- それぞれのデータからどれだけ離れているかの二乗を算出する。(その離れ具合を誤差という。)
- 全てのデータの誤差の二乗を合計をする。
- 3.の結果から、1.で作った関数の係数を決定し尤もらしい関数を作る。
では1つ1つみていきましょう。
1. 適当な関数を作っておく。
今回は直線っぽいので、1変数の関数を用意しました。
最小二乗法の最終目的はこの関数の$a, b$を求めることにあります。
\hat{y}_i = ax_i + b
ここで、変数の定義をしておきます。
$x_i, y_i$は$i$番目のデータの値です。
一方で、$\hat{y_i}$は$i$番目のデータの予測した値になります。
この$\hat{y_i}$を予測値などと呼んだりします。
またこの関数は、そのデータのばらつきに合わせて形を変える必要があります。
2. それぞれのデータの誤差の二乗を計算する。
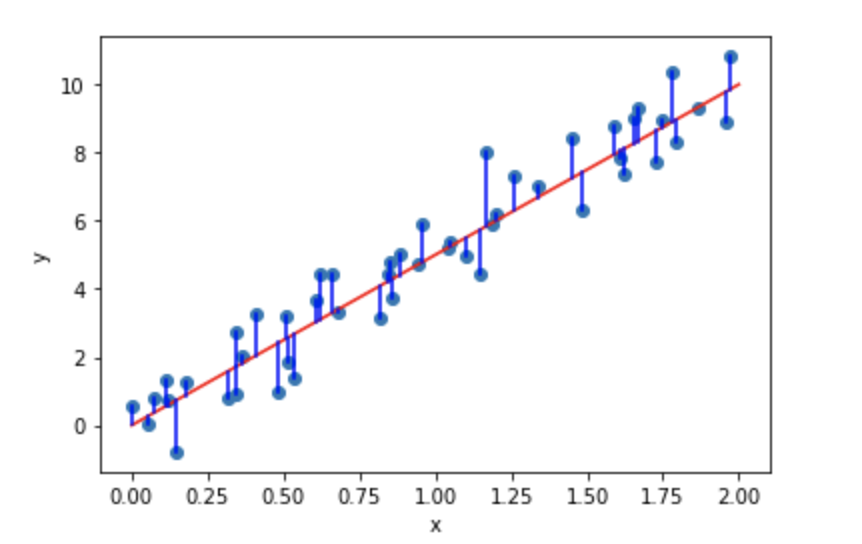
この青い線が誤差であり、この長さを1つ1つ調べていく必要があります。
数式上では誤差は以下のように書けます。
y_i - \hat{y_i} = y_i - (ax_i + b)
しかしこのままだと、$y_i, \hat{y_i}$の大小関係で正負が変化するため、純粋な誤差を求めることができません。
そこで、この誤差の値を二乗します。
すると誤差の二乗は、
(y_i - \hat{y_i})^2 = (y_i - (ax_i + b))^2
このように求めることができます。
このデータはおよそ$(x_{20}, y_{20}) = (0.6, 4.5)$であるので、
ので、$i=20$番目だと
\begin{align}
(y_{20} - \hat{y_{20}})^2
&= (y_{20} - (ax_{20} + b))^2\\
&= (4.5 - (a \times 0.6 + b))^2\\
&= \frac{9}{25}a^2+\frac{6}{5}ab +b^2-\frac{27}{5}a-9b+\frac{81}{4}
\end{align}
となります。
このようにして、50個全ての誤差の二乗を算出します。
3. 全てのデータの誤差の二乗を合計をする。
タイトル通り、2.で算出したものの和を出します。
数式で書くと、
\begin{align}
S
&=\sum_{i}^{N}{(y_i - \hat{y_i})^2} \\
&= \sum_{i}^{N}{(y_i - (ax_i + b))^2}\\
&= a^2(\sum_{i}^{N}x_i^2)+2a\sum_{i}^{N}{(bx_i-x_iy_i)}-2b\sum_{i}^{N}{y_i}+\sum_{i}^{N}y_i^2 + Nb^2
\end{align}
となります。
ここで、$N$はデータの数なので今回は50となります。
この関数$S(a, b)$が最小となる時の$a, b$が今回の求めたい変数となります。
4. aとbの決定
ここを決定するのが勾配法となります。
$S(a, b)$が凸関数となるので、最急勾配法などから関数の最小値を導きだします。
詳しくはその2で説明しようと思います。
ここまでは勾配法を行う上で必須の知識となりましたが、以降は数学的な観点が多く含まれますので、「そんなのいらねぇ!」って人は飛ばしてもらっても大丈夫です。
ヘッセ行列と半正定値
次の凸関数の説明に必要な概念です。
ヘッセ行列とは、
$n$変数関数 $f(x1,x2,⋯,xn)$ に対して,
$ij$成分が $\frac{∂^2f}{∂x_i∂x_j}$ であるような $n×n$ 行列をヘッセ行列と言う。
とあります。(参考2)
つまり、
\begin{pmatrix}
\frac{∂^2f}{∂x^2_1} & \cdots & \frac{∂^2f}{∂x_1∂x_j}\\
\vdots & \ddots & \vdots \\
\frac{∂^2f}{∂x_i∂x_1} & \cdots & \frac{∂^2f}{∂x_i∂x_j}\\
\end{pmatrix}
このような行列です。
みてもらったらわかるように、ヘッセ行列は対称行列です。
半正定値とは、以下のように定義されています。(参考1)
一般に,対称行列 $A$ が「任意のベクトル $x$ に対して $x^⊤Ax ≥ 0$」を満たすとき半正定値という.また,「任意のベク トル $x ≠ 0$ に対して $x^⊤Ax > 0$」を満たすとき正定値という.
半正定値である定義から、
- 全ての$n$ 次元実ベクトル $\bf{x}$ に対して二次形式 $bf{x}^⊤Abf{x}$ が非負
- $A$の固有値は全て非負
- ある実正方行列 $U$ が存在して $A=U^⊤U$ と表せる
- $A$ の主小行列式が全て非負
を満たす行列が、半正定値であるといえます。
また後ほど述べますが、ヘッセ行列$\Delta{S}$が半正定値である時、$S$は凸関数となります。
では準備が整ったところで、凸関数をみていきましょう。
凸関数
凸関数とは、局所解に陥らずに大域解にたどり着くために必要な概念です。
λf(x) + (1 − λ)f(y) ≥ f(λx + (1 − λ)y)\\
0 ≤ λ ≤ 1
以上の条件を成立させるものを、凸関数と言います。
噛み砕いて言うと、
「関数 $f$上に存在する点$P( = f(x))$, 点$Q( = f(y))$の間に存在する点$R( = f(z))$が直線$PQ$上に存在する点$S$より小さい時、凸関数と言う。」
となります。
最適化を行う関数が凸関数であれば、局所的最適解と大域的最適解が一致するという良い性質を持っています。
これは下の図をみてもらうと理解できると思います。


そこで、上で取り上げた、最小二乗法の関数$S$が凸関数であることを導きたいと思います。
$S$が凸関数であると言うには、$\Delta{S}$が半制定値であれば良いので、
\sum_{i}^{N}x_i^2 = s_{xx}, \sum_{i}^{N}x_i = s_x, \sum_{i}^{N}y_i^2 = s_{yy}, \sum_{i}^{N}y_i = s_y, \sum_{i}^{N}x_iy_i = s_{xy}
とおくと、
最小二乗法の関数$S$は、
\begin{align}
S
&=a^2s_{xx}+2as_x-2as_{xy}-2bs_y+s_{yy}+Nb^2
\end{align}
となります。
これをそれぞれ$a, b$で偏微分してみると
\begin{align}
\frac{∂Q}{∂a}&=2s_{xx}a + 2s_xb - 2s_{xy}\\
\frac{∂Q}{∂b}&=2s_{x}a + 2Nb - 2s_{y}
\end{align}
なのでこれを元に$S$をヘッセ行列にすると
\begin{align}
\Delta{S}
&=
\begin{pmatrix}
\frac{∂^2f}{∂x^2} & \frac{∂^2f}{∂x∂y} \\
\frac{∂^2f}{∂y∂x} & \frac{∂^2f}{∂y^2}
\end{pmatrix}\\
&=
2
\begin{pmatrix}
s_{xx} & s_x \\
s_x & n
\end{pmatrix}
\end{align}
となります。
上の半正定値である条件1から、「$\Delta{S}$の2次形式が非負である」ことを示せばよいです。
$\sum_{i}^{N}x_i^2 = s_{xx}, \sum_{i}^{N}x_i = s_x$であるので、
\begin{align}
2
\begin{pmatrix}
t & k
\end{pmatrix}
\begin{pmatrix}
s_{xx} & s_x \\
s_x & n
\end{pmatrix}
\begin{pmatrix}
t\\
k
\end{pmatrix}
&=
2(s_{xx}t^2+2s_xtk + Nk^2)\\
&=
2(t^2\sum_{i}^{N}{x_i^2}+2tk\sum_{i}^{N}{x_i}+Nk^2)\\
&=
2\sum_{i}^{N}{(t^2x_i^2+2tkx_i+k^2)}\\
&=
2\sum_{i}^{N}{(tx_i+k)^2} ≥0
\end{align}
$\Delta{S}$は半正定値であるので、最小二乗法によって作られた目的関数$S$は凸関数であることが証明できました。
これより、最小二乗法で作られる関数は凸関数であり、局所解が最適解としても成り立つことがわかります。
詳しくは参考1参考5を見てみてください。
証明までしているので非常にわかりやすかったです。
また、画像は参考6から引用させてもらいました。
微分の定義
ここで、次に説明する$Armijo$のルールで使う微分の定義を説明します。
{\nabla}f(x_k)={\lim_{h \to 0}}\frac{f(x+h)-f(x)}{h}
ここで誤差を$o(h)$とおくと、
o(h) = \frac{f(x+h)-f(x)}{h} - {\nabla}f(x_k)
\begin{equation}
f(x+h) = f(x) + h{\nabla}f(x_k) + ho(h)\tag{1}
\end{equation}
と表現することができます。
勿論、この$o(h)$は
\lim_{h \to 0}o(h) = 0
となりますが、$h$が十分に小さくない値を取る時、$o(h)$は特定することができなくなります。
Armijoのルール
$Armijo$(アルミホ)のルールとは、学習率 $t$を選定する手法の1つです。
$k$を学習した回数として、今回の目的関数を$f(x_k)$と設定します。
$x_k$から次の座標の$x_{k+1}$に進むためには、降下方向$d_k$に向かって、学習率$t_k$だけ進むとします。
すると
\begin{equation}
f(\textbf{x}_{k+1})=f(\textbf{x}_k + t_k\textbf{d}_k)\tag{2}
\end{equation}
と書くことができます。
ここで初めて出てきた降下方向$d_k$とは、
\begin{equation}
{\nabla}f(\textbf{x}_k)^\mathsf{T}\textbf{d}_k<0\tag{3}
\end{equation}
を満たすベクトルのことです。
これは、傾き$\nabla{f(x_k)}$が正であれば負の方向に、傾き$\nabla{f(x_k)}$が負であれば正の方向に降下していくことを考えると納得できます。
また、$d_k$は方向が重要なだけなので長さは$1$で構いません。
話を戻して、(2)式を(1)式を参考にして変形すると
f(\textbf{x}_k+t_k\textbf{d}_k) = f(\textbf{x}_k) + t_k{\nabla}f(\textbf{x}_k)^\mathsf{T}\textbf{d}_k + t_ko(t_k)
と変形できます。
これを、ステップ前と比べてみると
\begin{align}
f(\textbf{x}_{k+1}) - f(\textbf{x}_k) &=
f(\textbf{x}_k+t_k\textbf{d}_k) - f(\textbf{x}_k)\\ &= t_k{\nabla}f(\textbf{x}_k)^\mathsf{T}\textbf{d}_k + t_ko(t_k)\\
&= t_k({\nabla}f(\textbf{x}_k)^\mathsf{T}\textbf{d}_k + o(t_k))\tag{4}
\end{align}
となります。
ここで、$o(t_k)$は上で述べたように誤差であるため、$t_k$が大きくなるほどその値が変化しますが、$t_k$が十分に小さな値となる時は無視することができます。
$t_k$を$o(t_k)$が無視できるほど小さな値にすると、(3)式の条件から(4)式の右辺は負になることがわかります。
また、(4)式の左辺も大前提として$f(x_{k+1}) < f(x_k)$であるので、当たり前に負です。
以上のことから、(4)式を少し弄ると
f(\textbf{x}_{k+1})-f(\textbf{x}_k) ≤ \gamma\beta^{l_k}{\nabla}f(\textbf{x}_k)^\mathsf{T}\textbf{d}_k\tag{5}\\
ただし、それぞれの変数は以下の設定します。
\begin{cases}
\begin{align}
\gamma, \beta &\in (0, 1)\\
t_k &= \beta^{l_k}\\
l_k &= 0, 1, 2, 3 \cdots
\end{align}
\end{cases}
この条件式が、$Armijo$のルールです。
つまり、この式を満たす$t$が学習率として選ぶことができるということです。
では早速(5)式を噛み砕いていきます。
(5)式は両辺とも負であるはずなので、$\gamma$がかけられている右辺は左辺より大きくなります。
左辺が鬱陶しいのでまとめると、
\begin{align}
p(t_k)
&= f(\textbf{x}_k+t_k\textbf{d}_k) - f(\textbf{x}_k)\tag{6}\\
(&= f(\textbf{x}_k+\beta^{l_k}\textbf{d}_k) - f(\textbf{x}_k))\\
\end{align}
となります。
またこれを$t_k$で微分してみると、
\frac{d}{dt_k}p(t_k) = {\nabla}f(\textbf{x}_k+t_k\textbf{d}_k)^\mathsf{T}\textbf{d}_k\\
\frac{d}{dt_k}p(0) = {\nabla}f(\textbf{x}_k)^\mathsf{T}\textbf{d}_k\tag{7}
と変形することができます。
(5)式に似た部分があるので(5)式を、(6),(7)式で置き直してみると、
p(t_k) ≤ {\gamma}\frac{d}{dt_k}p(0)t_k\tag{8}
となります。
$\frac{d}{dt_k}p(0)$は、$p(t_k)$の$t_k=0$における接線の傾きであるため、以下のように$\gamma=1$の時は赤線のように$t_k=0$における$p()t_k$の接線となります。
一方、$\gamma$は$0$に近づくにつれて青線のように、傾きは$0$に収束していきます。

またここで$\beta = 0.5$とすると、
| $l_k$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ |
|---|---|---|---|---|---|---|---|---|
| $t$ | $1$ | $0.5^{1}$ | $0.5^{2}$ | $0.5^{3}$ | $0.5^{4}$ | $0.5^{5}$ | $0.5^{6}$ | $0.5^{7}$ |
| となります。 | ||||||||
| $l_k$は$0$以上の整数値しか取らないため、$l_k$が増加すると$t_k$は減少し、その範囲は |
0<t_k≤1
となります。
学習率は出来るだけ大きな方が効率が良いですので、$l_k$を$0$から増加させていき、(5)式を満たす値を学習率として採用します。
このルールを用いることで、学習率の選定が最適に選ぶことができます。
ただしこの問題を実装するためには、$p'(t)$の形をあらかじめ推測して置く必要があるため、使用する際には工夫が必要になります。
最後に
今回で勾配法に必要な理論をある程度固めることができました。
機会があれば、実際の手法を用いて理解を深めていきたいと思います。
参考文献
・参考1: 最適化と凸関数 (東京大学講義資料)
・参考2: 多変数関数の極値判定とヘッセ行列
・参考3: 降下法 (京都大学講義資料)
・参考4: 制約なし最適化問題(名古屋大学講義資料)
・参考5: 確率的勾配降下法のメリットについて考えてみた
・参考6: 機械学習をやる上で知っておきたい連続最適化

