はじめに
k近傍法に引き続き、線形回帰モデルを使って車の燃費を予測してみました。
学習メモなので基本用語の詳しい解説などは書いていません。あしからず。
前の記事は以下
前提知識
実装に際して前提となる超基本知識をまとめました。
線形回帰 (Linear regression)
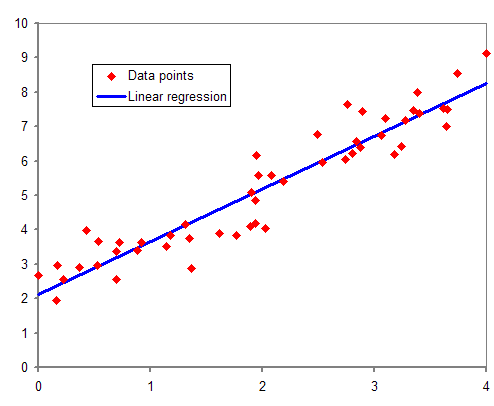
ある変数が与えられたときに、それと相関関係のある値を予測することを回帰分析と呼びます。
多数のデータをプロットし、直線を引いてモデルをつくることで、変数の相関値を予測できるようになります。
つまり、予測の精度をできるだけ高くできるように直線を引くこと(= 適切な傾きと切片を与えること)がとても大事になります。
平均二乗誤差(Mean Square Error)
平均二乗誤差とは、線形回帰モデルの性能を数値化する効果的な手法の一つで、実際の値とモデルによる予測値との誤差の平均値のことをいいます。

勾配降下法 (Gradient Descent)
MSEができるだけ小さくなるような直線の傾き(m)と切片(b)を設定するために、勾配降下法を使用します。
MSEをb(もしくはm)で微分したときの値が最小になったときに、MSEを最小にするb(もしくはm)を導出するといった手法になります。
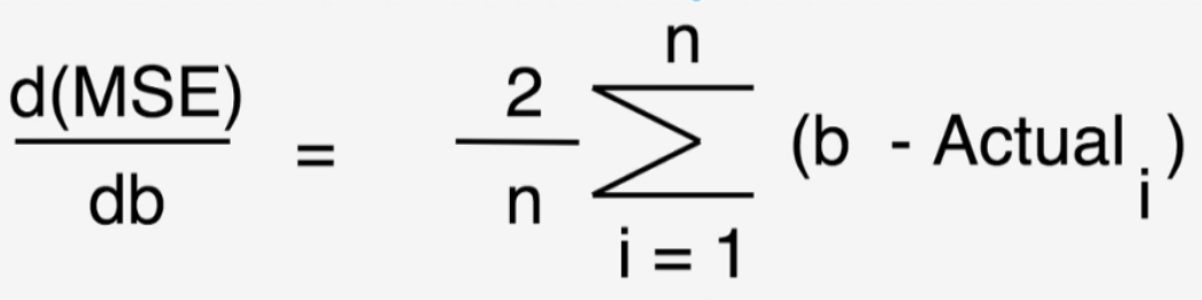
導出手順は以下のようになります。
- MSEをbで微分
- 微分値が最小であるか判定 -> 最小であればbを決定(ここで終了)
- 最小でなければ学習率(Learning Rate)をかける
- b = b - (3で導出した値)とする
- 2に戻る
実装
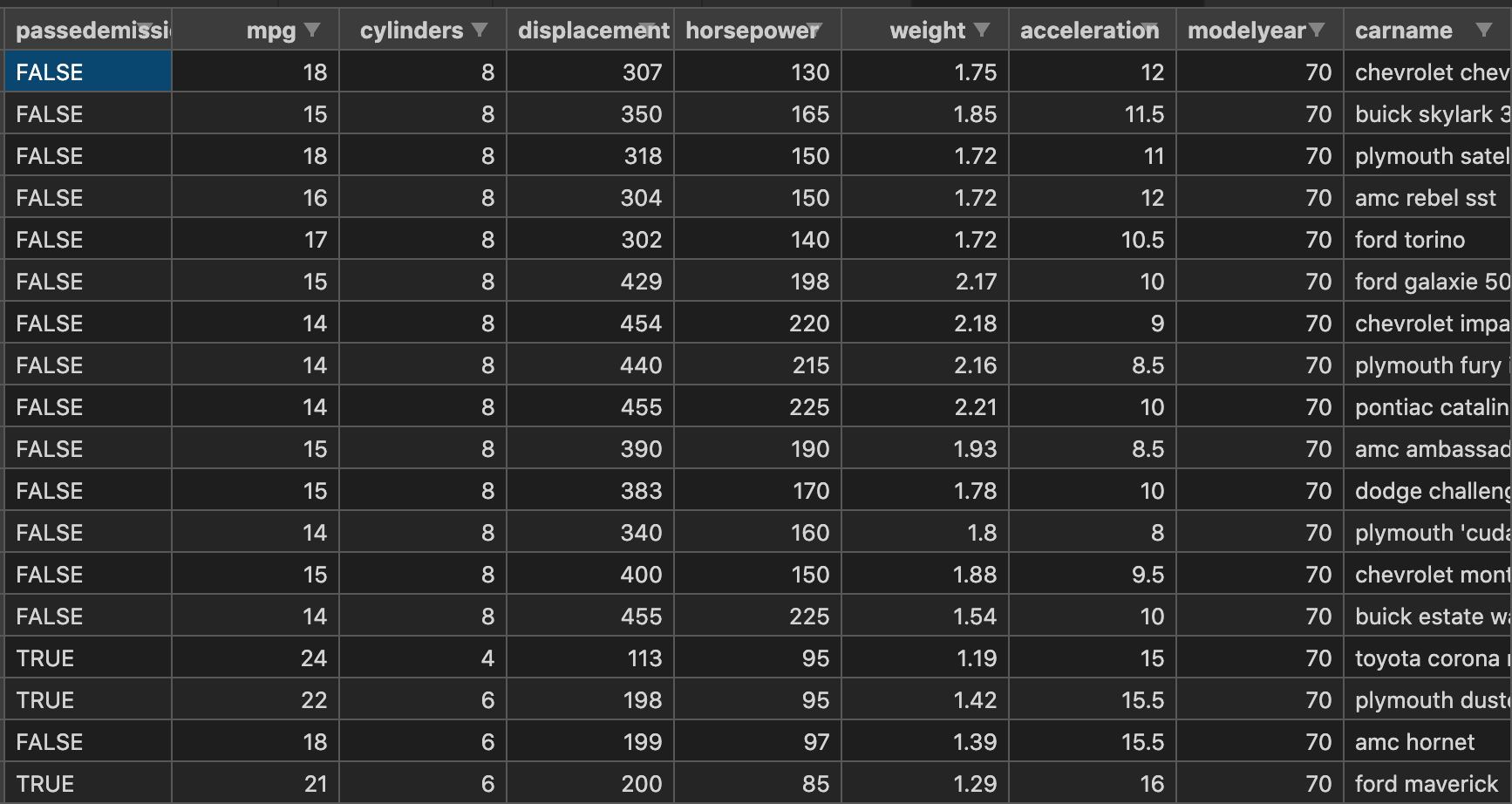
horsepower(馬力), weight(重量), displacement(エンジンの大きさ)を入力値として、mpg(燃費)を予測します。
メソッドの構成
線形回帰を実装するにあたり、LinearRegressionクラスを作成し、各メソッドに機能をわけました。
- gradientDescent(): 勾配降下処理の実行とm, bの更新
- train(): 最適なm, bがでるまでgradientDescent()を実行
- test(): Test dataから導出したm, bの精度を評価
- predict(): 導出したm, bで値を予測
- processFeatures(): 計算に使えるようにfeaturesを加工
- standardize(): データの標準化
- recordMSE(): 学習率の調整に使えるようにMSEを記録
- updateLearningRate(): 学習率の更新
コード① linear-regression.js
コードにするとこのような感じになりました。
//ライブラリの読込
const tf = require('@tensorflow/tfjs');
const _ = require('lodash');
//クラス
class LinearRegression {
constructor(features, labels, options) {
this.features = this.processFeatures(features); //
this.labels = tf.tensor(labels); //
this.mseHistory = [];
this.options = Object.assign(
{ learningRate: 0.1, iterations: 100 },
options
);
this.weights = tf.zeros([this.features.shape[1], 1]); //m, bの初期値
}
gradientDescent(features, labels) {
const currentGuesses = features.matMul(this.weights); //features * weights
const differences = currentGuesses.sub(labels); // features * weights - labels
// dMSE/dmとdMSE/dbのテンソル
// (features * (features * weights - labels))/n
const slopes = features
.transpose()
.matMul(differences)
.div(features.shape[0]); //列の個数で割る
this.weights = this.weights.sub(slopes.mul(this.options.learningRate)); //m, bのテンソル
}
train() {
//バッチの個数(データ個数/1回のバッチサイズ)
const batchQuantity = Math.floor(
this.features.shape[0] / this.options.batchSize
);
// 学習率を最適化しながらMSEを繰り返し実行
for (let i = 0; i < this.options.iterations; i++) {
for (let j = 0; j < batchQuantity; j++) {
const startIndex = j * this.options.batchSize; //バッチ開始位置
const { batchSize } = this.options; //1回のバッチサイズ
//各バッチのfeatures
const featureSlice = this.features.slice(
[startIndex, 0],
[batchSize, -1]
);
//各バッチのlabels
const labelSlice = this.labels.slice([startIndex, 0], [batchSize, -1]);
//バッチごとにgradientDescentを実行
this.gradientDescent(featureSlice, labelSlice);
}
this.recordMSE();
this.updateLearningRate();
}
}
predict(observations) {
return this.processFeatures(observations).matMul(this.weights);
}
//決定係数の導出
test(testFeatures, testLabels) {
testFeatures = this.processFeatures(testFeatures);
testLabels = tf.tensor(testLabels);
const predictions = testFeatures.matMul(this.weights);
const res = testLabels.sub(predictions).pow(2).sum().get(); //Sres
const tot = testLabels.sub(testLabels.mean()).pow(2).sum().get(); //Stot
return 1 - res / tot; //coefficient of determination(決定係数)
}
//計算に使えるようにfeaturesを加工
processFeatures(features) {
features = tf.tensor(features);
features = tf.ones([features.shape[0], 1]).concat(features, 1);
if (this.mean && this.variance) {
features = features.sub(this.mean).div(this.variance.pow(0.5)); //正規化
} else {
features = this.standardize(features); //標準化
}
return features;
}
//標準化
standardize(features) {
const { mean, variance } = tf.moments(features, 0);
this.mean = mean;
this.variance = variance;
return features.sub(mean).div(variance.pow(0.5));
}
//学習率(Learning Rate)調整のためにMSEを記録
recordMSE() {
const mse = this.features
.matMul(this.weights)
.sub(this.labels)
.pow(2)
.sum()
.div(this.features.shape[0])
.get();
this.mseHistory.unshift(mse);
}
//学習率(Learning Rate)の更新
updateLearningRate() {
if (this.mseHistory.length < 2) {
return;
}
if (this.mseHistory[0] > this.mseHistory[1]) {
this.options.learningRate /= 2;
} else {
this.options.learningRate *= 1.05;
}
}
}
module.exports = LinearRegression;
決定係数(Coefficient of Determination)
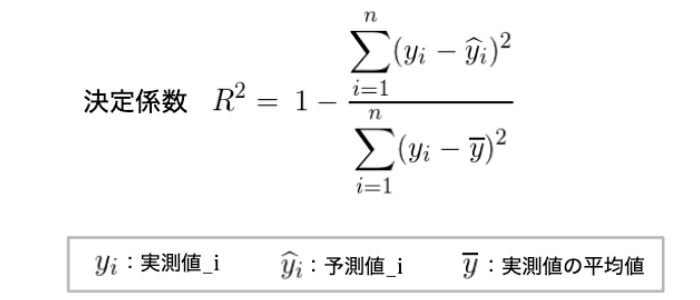
test()メソッドで出力する予測精度として、決定係数というものを考えました。
決定係数は、回帰によって導いたモデルで予測した値が実際の値とどの程度一致しているかを表現する評価指標です。
決定係数はR2として表現され、値が大きいほどモデルが適切にデータを表現できていること(予測値の精度が高いこと)を意味します。
バッチ勾配降下法
勾配降下法はパラメータの更新のたびにすべてのTraining dataで勾配を計算します。
Training dataの量が増加するにつれて計算を行うのが難しくなるため、その場合はバッチ勾配降下法や確率的勾配降下法を利用します。
バッチ勾配降下法では、一度に利用するTraining dataの量が勾配降下法と比較して少なくなります。
Training dataの中からいくつかのデータを取り出し、そのデータで計算した勾配にもとづいてパラメータを更新します。
勾配降下法と比較すると計算に必要なメモリ量が少なく、確率的勾配降下法と比較すると外れ値の影響を受けにくく学習が比較的安定して進むという利点があります。
train()メソッドではbatchQuantityでバッチの個数(回数)を定義し、1回のiterationごとにその回数gradientDescent()を実行しています。
学習率(Learning Rate)の最適化
勾配降下法(gradientDescent)で使用する学習率(Learning Rate)は、MSEの導出ごと(1回のiterationごと)に最適化を行います。
- MSEの導出と記録
- 1回前のMSEと新しいMSEの値の比較
- MSEが大きくなっていたら学習率を1/2にする
- MSEが小さくなっていたら学習率を5%増やす
コード② index.js
index.jsでlinear-regression.jsを読み込んで、決定係数(R2)とm, bを出力してみました。
require('@tensorflow/tfjs-node'); //ルートフォルダで1回だけ呼ぶ
const tf = require('@tensorflow/tfjs');
const loadCSV = require('../load-csv');
const LinearRegression = require('./linear-regression');
const plot = require('node-remote-plot');
let { features, labels, testFeatures, testLabels } = loadCSV(
'../data/cars.csv',
{
shuffle: true,
splitTest: 50,
dataColumns: ['horsepower', 'weight', 'displacement'],
labelColumns: ['mpg'], //Miles Per Gallon
}
);
const regression = new LinearRegression(features, labels, {
learningRate: 0.1,
iterations: 100,
batchSize: 10,
});
regression.train();
const r2 = regression.test(testFeatures, testLabels);
plot({
x: regression.mseHistory.reverse(),
xLabel: 'Iteration #',
yLabel: 'Mean Squared Error',
});
console.log('R2 is', r2);
console.log(
'Updated M is:',
regression.weights.get(1, 0),
'Updated B is:',
regression.weights.get(0, 0)
);
regression.predict([[120, 2, 380]]).print();
結果
R2 is 0.6592028145756478
Updated M is: -1.645716905593872 Updated B is: -23.4530029296875
また、iterationごとのMSEの変遷をplotでグラフにすると以下のようになりました。

おわりに
確率的勾配降下法を使うとどんな結果になるのかも試してみたいです。
参考資料