本文の目的
ZDD というアルゴリズムを鉄道網に適用し、ある始点から別の始点までのパスの個数を効率的に数えることを目的とする.これにより、計算量を軽減し、より広範囲のstパスの個数を把握する.また、得られたデータをプログラミングで利用しやすくするための処理と、作成したプログラムが実際にどれほどのデータ量を処理できるかについて考察する.
作成した主なコード
githubのrepositoryに用いた主なコードをまとめました.
用語定義
・stパス
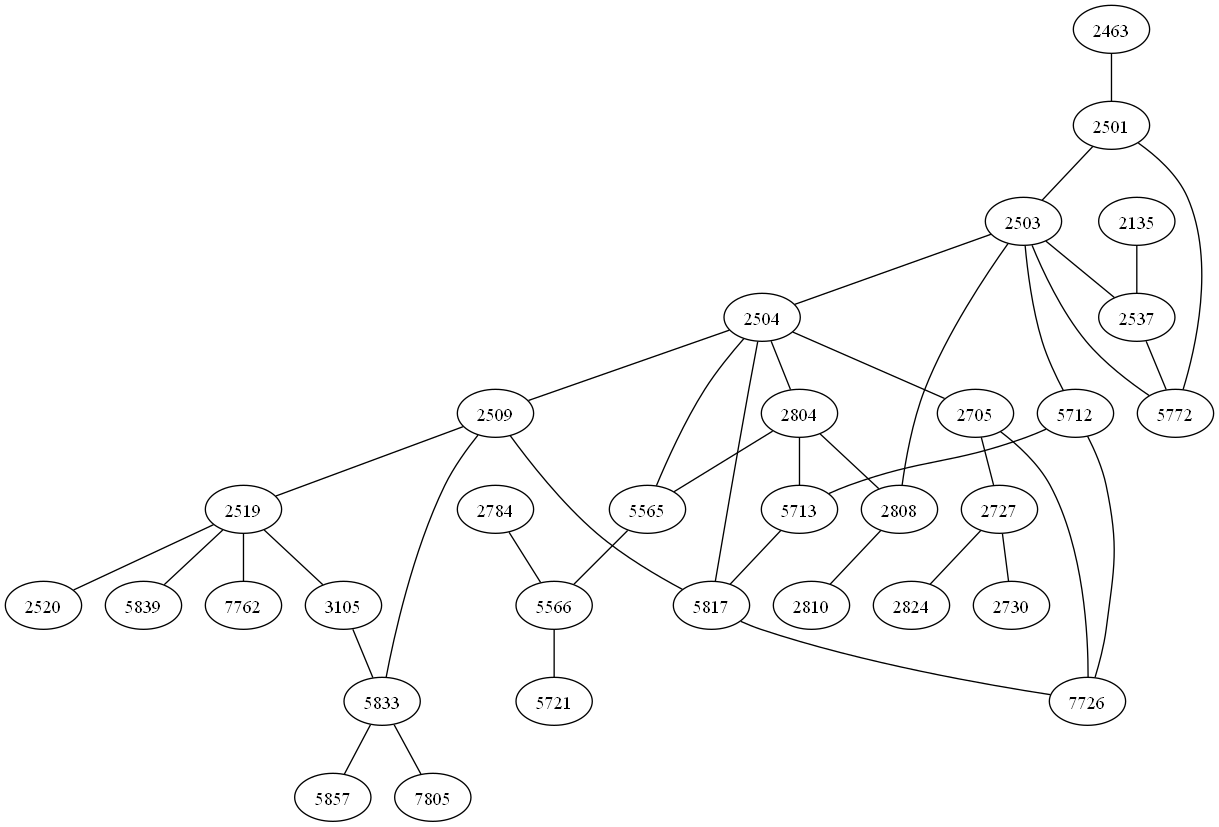
stパスは、グラフの頂点集合 V と辺集合 E において、始点 s と終点 t の間に存在する頂点の列 $v_{1}, v_{2}, ..., v_{n}$ であり、各隣接する頂点対 $(v_{i},v_{i+1}) $ が辺集合 E に含まれている場合の経路を指す.例えば,下の図においてノード番号 1 を始点,ノード番号 5 を終点としたとき,赤のエッジで示された経路はstパスである.
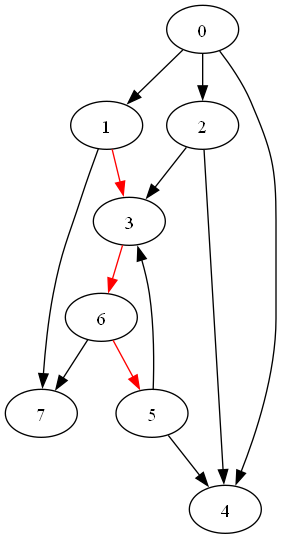
・stパス数え上げ問題
あるグラフでのstパスの個数を求める問題.例えば上の図においては始点をノード 1,終点をノード 5 とした時,他のstパスはグラフ上に存在しえないため,stパスの個数は1個である.
はじめに
「お姉さん問題」という有名な問題がある.「お姉さん問題」とは、N × N のマス目があり、左上のスタートから右下のゴールまで、遠回りしてもよいので何通りの道順が取れるかを問う問題である.この問題は stパス数え上げ問題の代表的な例として知られており、特に現在最も広く用いられている解法の1つである ZDD(Zero-suppressed Decision Diagram)は、鉄道網への適用例も存在する.(詳しくはこちら https://www.edu.kobe-u.ac.jp/istc-tamlab/cspsat/pdf-open/cspsat2_seminar06_nakamoto.pdf )

以下は,「お姉さん問題」についてのyoutubeの動画のリンク
https://www.youtube.com/watch?v=Q4gTV4r0zRs&t=314s
お姉さん問題のNの大きさを変化させた際のstパス数は以下の通りである.
表1: 各 N におけるstパスの個数
| N | stパス数 |
|---|---|
| 1 | 2 |
| 2 | 12 |
| 3 | 184 |
| 4 | 8512 |
| 5 | 1262816 |
| 6 | 575780564 |
| 7 | 789360053252 |
| 8 | 3266598486981642 |
このように組み合わせは N に対して指数的に増加する.そしてそれに伴い組み合わせの数え上げも工夫せずに全探索で数え上げると指数的に計算量が増加する.これは,全探索の際グラフに存在する全ての辺に対して,その辺がstパスに含まれるor含まれないかの2通りが存在し,ゆえに辺の数を E とすると考えなくてはいけない状態数は $ 2^{E} $ となるからである.(これはあるグラフの辺集合のべき集合を全て考えていることに等しい.)
例として上の N=8 のグラフを考えてみることにする.この時,その辺数は 144 であり,そのべき集合の要素数は $2^{144}$ である.つまり約 $2.23×10^{43}$ 個要素数が存在する.ここでみなさんが持っているであろう一般的なパソコンは一秒間に四則演算約 $1×10^{8}$ 個の処理が可能であるとされている.仮に,考えたべき集合がstパスをなしているかの判定が四則演算1つ分で可能であるとしても,$ 2.23×10^{35} $秒,つまり$ 7.07×10^{27} $年かかる.これは宇宙が誕生してから今に至る時間の 512318840579710144 倍である.つまり,工夫が当然必要であり,トップダウン法を用いて ZDD を作成する.
1.トップダウン法の基本的概念の解説
トップダウン法の基本的な概念は前回の記事に乗せているのでそれを参照してほしい.(前回記事 https://qiita.com/sunagimo3/items/76f6127c419512fa622b)
ここでは簡単にトップダウン法で ZDD を作成する際に重要となる4つの概念を再掲していく.
1.ノード生成の手法
i 番目の層に存在するノード $\alpha$ は、(i+1) 番目の層に 0 枝と 1 枝の有向枝を伸ばし、新たに (i+1) 番目の層に存在するノードを生成する.このプロセスを1つの根ノードから繰り返すことで、ZDD を構成するのがトップダウン法である.
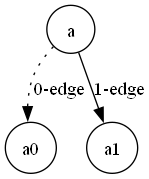
図1: ノード a から出る 0枝 と 1枝
2.グラフの共有
それぞれのノードは元の要素 $x^{n} = {x_{1}, x_{2}, x_{3}, \ldots, x_{n}}$ のべき集合の1つの要素を表している.この集合における「ある集合が解の要素になるか」に関する情報を configuration と呼び、ノード $\alpha$ に対する configuration を $\phi(\alpha)$ とする.ここで,$\phi(\alpha) = \phi(\beta)$ が成立するとノード $\alpha$ と ノード $\beta$ を共有することができる.これにより、ノード数を削減し、計算量を減らすことができる.

図2: 共有する前の図 |

図3: 共有した後の図 |
3.False枝刈り
あるノードから下の層ラベルに伸ばしたノードがその時点で解にならないことが判明した時そのエッジの終点をFalseに接続させる手法を False枝刈り と呼ぶ.枝刈りをおこなうことであるノードの子孫のノードを全て削減することができ,計算量を削減することができる.
4.True枝刈り
あるノードから下の層ラベルに伸ばしたノードがその時点で解になることが判明した時そのエッジの終点をTrueに接続させる手法を True枝刈り と呼ぶ.
 図4: False枝刈りの例 |
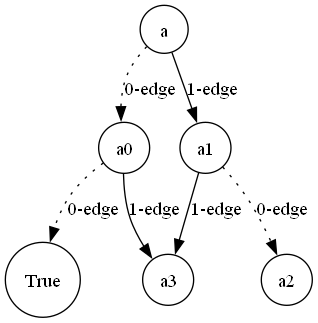 図5: True枝刈りの例 |
これらの手法を用いてstパスにおいてn個の辺を持つグラフの辺集合 $E^{n}$=$(e_{1},e_{2},...,e_{n})$ のべき集合を表現するような ZDD をトップダウン法を用いて作成していくことを考える.
2.トップダウン法をstパス数え上げ問題に適用する
上で述べた概念を用いて,stパス数え上げ問題に対して ZDD を適用させていく.
1.False枝刈り
以下の3つの条件のいずれかを満たした場合,False枝刈り をすることができる.
(1).始点または終点の次数条件
stパスの図においては必ず始点と終点の次数はどちらも1である.つまり,
「stパスのグラフ⇒始点と終点の次数はどちらも1」であり対偶をとると
「始点または終点の次数が1でない(∴0または2以上)⇒stパスのグラフでない」
よって「始点または終点の次数が2以上になったときまたは次数が0であることが確定した時」に False枝刈り を行える.
(2).始点,終点以外の頂点の次数条件
stパスの図においてstパスに含まれる頂点の次数は2,含まれない頂点の次数は0である.よって,「stパスのグラフ⇒始点終点以外の頂点の次数が0または2である」であり対偶をとると「始点終点以外の頂点の次数が0または2でない(1または3以上である)⇒stパスのグラフでない」ことが導かれる.よって,「始点終点以外の頂点の次数が3以上または1であることが確定した時」に False枝刈り を行える.
(3).ループが生じる
stパスにはループが存在しないため、ループが生じた場合は False枝刈り が可能である.
2.True枝刈り
False枝刈り によって削除されなかった部分グラフの内,既に始点と終点が同じ連結成分に所属していれば True枝刈り が行える.これは False枝刈り によって全ての不適な場合のグラフを削除で来ているので,残ったグラフの内始点と終点が同じ連結成分に含まれていたらそのグラフはstパスであると判定できるからである.
3.configuration
さて,「この問題のある集合が解の要素になるか」の部分はグラフがstパスであることである.この時, configuration は2つ存在する.
1つ目は各ノードが表す部分グラフの頂点の次数と考えることができ,それをn個の要素を持つ1次配列 deg とおき,ノード $\alpha$ が表現する各グラフの n 個の頂点の各 v の次数を $deg(\alpha)$ = [$deg_{v_{1}}(\alpha),deg_{v_{2}}(\alpha),...,deg_{v_{n}}(\alpha)$] ($deg_{v}(\alpha)$ は v の次数)と定義する.
2つ目はノードが表現するグラフの連結成分を記憶する n 個の要素を持つ comp という配列を用意する.頂点 $v_{1}$ と $v_{2}$ がグラフの同じ成分に含まれるのであれば comp[$v_{1}$] = comp[$v_{2}$],含まれないならば,comp[$v_{1}$] ≠ comp[$v_{2}$]である.また,comp[$v_{i}$] の初期値は i である.また,i 番目の層ラベルに存在するノードの 1枝 を採用し,(i+1) 番目の層ラベルのノードに遷移したとする.この時,採用した辺の両端の頂点が $v_{1},v_{2}$ であるとすると,comp[$v_{1}$] = min($comp[v_{1}]$,$comp[v_{2}]$),comp[$v_{2}$] = min($comp[v_{1}]$,$comp[v_{2}]$)と comp の値を変化させる.
4.ノード生成
層ラベル i に存在するノード $\alpha$ から出た 0枝 と 1枝 の終点を $\alpha_{0},\alpha_{1}$,i番目 のエッジ $e_{i}$ の両端を $a_{i}$と$b_{i}$ とすると $deg_{a_{i}}(\alpha_{1}) = deg_{a_{i}}(\alpha) + 1$,$deg_{b_{i}}(\alpha_{1}) = deg_{b_{i}}(\alpha) + 1$,$deg_{a_{i}}(\alpha_{0}) = deg_{a_{i}}(\alpha)$,$deg_{b_{i}}(\alpha_{0}) = deg_{b_{i}}(\alpha)$というように遷移する.
また,前述のように $e_{i}$の両端が $a_{i}$,$b_{i}$ である時,$comp_{a_{i}}(\alpha_{1})$=$min(comp_{a_{i}}(\alpha),comp_{b_{i}}(\alpha))$,$comp_{b_{i}}(\alpha_{1})$=$min(comp_{a_{i}}(\alpha),comp_{b_{i}}(\alpha))$であり,0枝 を選択した場合の連結状態の変化はないので $comp_{a_{i}}(\alpha_{0})=comp_{a_{i}}(\alpha)$,$comp_{b_{i}}(\alpha_{0})=comp_{b_{i}}(\alpha)$ である.
以上の手法で「お姉さん問題」を実際にトップダウン法で行ったのがソースコードのoneesannmonndai.cppである.(動してみたところ n=6 までは1分以内に動いた.実装に詳しい人がいれば改善してさらにソースコードを改善してみるとよいかも)
3.鉄道網への応用
さて,stパスの数え上げのアルゴリズムをせっかく作ったので応用しようぜということで鉄道網に対してstパスの数え上げを適用していこうと考える.使用したのが駅データ.jpというサイトである.(https://ekidata.jp)
①このデータを加工し使える状態にする→②本質的にstパスの個数に寄与しないノードを減らしていく→③その最終的に縮約しきったデータをプログラムで動かす→④考察という手順でZDDの理論を鉄道網に応用していきたい.
ここでデータの処理は決定図の本質的な話とはそれるので①,②の部分は以下の記事で述べようと思う.興味があれば右の記事にどうぞ.(https://qiita.com/sunagimo3/items/e671f3f3e4493acbc0c5)
4.駅データへの適応
stパス数え上げを実装したのが~.cppである.このプログラムを日本全国の路線図全てを対象に行ったところ処理が膨大であるためプログラムが実行できなかった.そこで東京,京都,名古屋を中心とした部分グラフに対してプログラムを実行し,その結果を得た.
部分グラフの取り方
ある地点 $\alpha$ を中心とした大きさ D の部分グラフ S を以下のように定義した.
ある頂点 a,b 間の最短距離を distance(a,b) と表記することにして,グラフのあるエッジ $e=(v_{1},v_{2})$ は,
D≧min(distance($\alpha,v_{1}$)+1,distance($\alpha,v_{2}$)+1) を満たせば e は S に含まれ,
D<min(distance($\alpha,v_{1}$)+1,distance($\alpha,v_{2}$)+1) を満たせば e は S に含まれない.
(最短距離はダイクストラ法によって求めた.ダイクストラ法のソースコードはdikstra.cpp)
この定義の下で,東京,京都,名古屋を中心とした部分グラフを得たところ,それぞれ半径が 2,3,3 の部分グラフに対してはプログラムが正常に実行した.
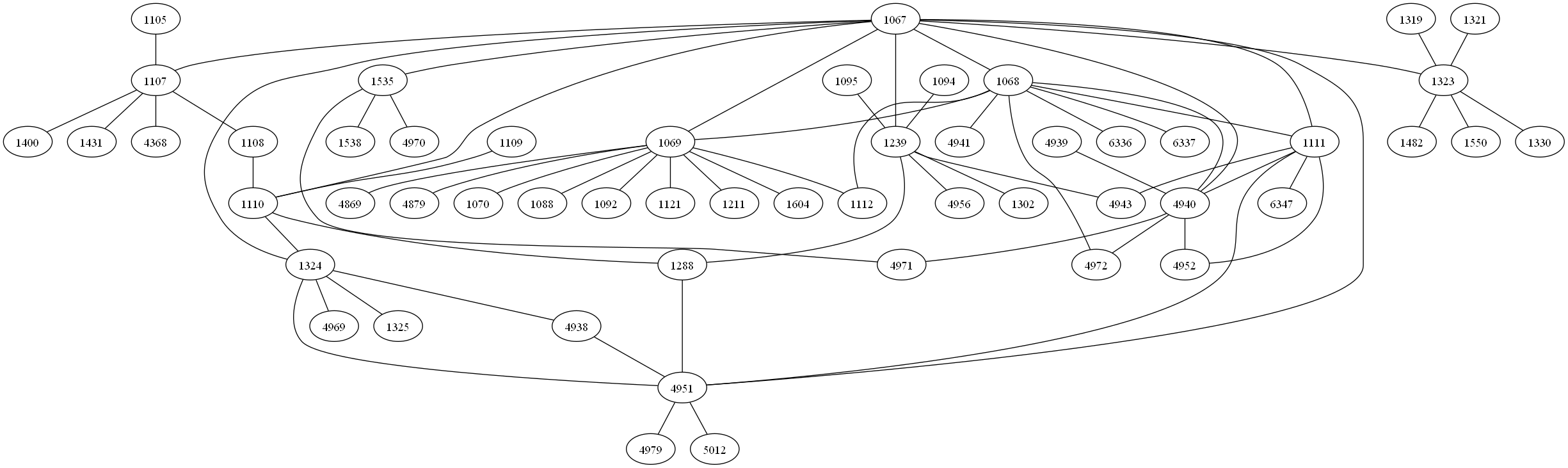
図6: 東京を中心とする大きさ 2 のグラフ
図7: 京都を中心とする大きさ 2 のグラフ
図8: 名古屋を中心とする大きさ 3 のグラフ
この得られたグラフの2点を重複しないようにランダムに選び,一方を始点,他方を終点とする.そのstパスを数え上げる操作を100回for文で行ったのがソースコード~.cppであり,その結果が以下.
表2:各グラフのエッジ数
| グラフ | エッジ数 |
|---|---|
| 東京を中心とした大きさ 2 の部分グラフ | 68 |
| 京都を中心とした大きさ 3 の部分グラフ | 40 |
| 名古屋を中心とした大きさ 3 の部分グラフ | 48 |
表3:各グラフのstパスの数の平均(n=100)
| グラフ | stパス数の平均 |
|---|---|
| 東京を中心とした大きさ 2 の部分グラフ | 429.73 |
| 京都を中心とした大きさ 3 の部分グラフ | 67.91 |
| 名古屋を中心とした大きさ 3 の部分グラフ | 740.2 |
表4:各グラフの実行時間(n =100)
| グラフ | 実行時間(s) |
|---|---|
| 東京を中心とした大きさ 2 の部分グラフ | 226.886 |
| 京都を中心とした大きさ 3 の部分グラフ | 31.3842 |
| 名古屋を中心とした大きさ 3 の部分グラフ | 436.723 |
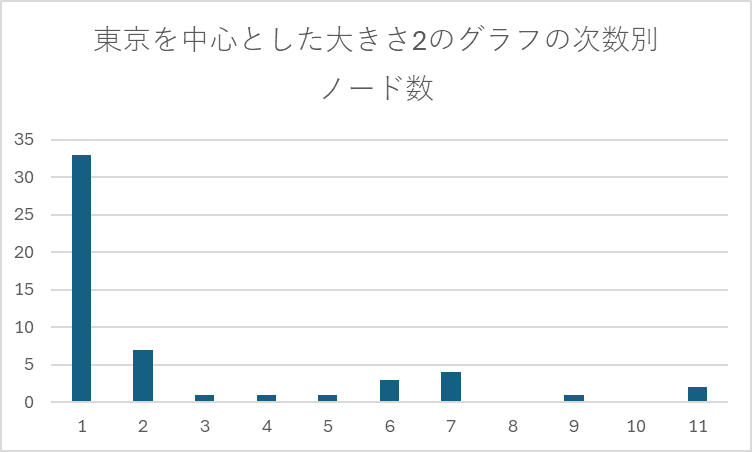
この上3つの表からstパス数の平均と実行時間には正の相関があることがわかる.これはstパス数が多いということは False枝刈り ができるケースが少なく,ZDDにおいてノード数が多くなりその分計算量が多くなることが考えられるからである.また,東京,名古屋を中心としたグラフを比べると名古屋を中心としたグラフのエッジ数の方が東京を中心としたグラフのエッジ数より少ないのにstパスの数と実行時間は多くなっている.この理由はグそれぞれのグラフの特徴にあると考え,それぞれのグラフの次数を求め,棒グラフにまとめると以下のようになった.

|

|
|
図9:各グラフの次数別ノード数の分布(横軸:次数,縦軸:ある次数のノードの数)
これを見ると,東京を中心とするグラフにおいて次数が 1 のノードが30個以上あり,名古屋のグラフにおいて次数が 3 や 4 のノード数が東京の数倍存在している.一般に次数 1 のノードはそのノードを消去してもstパスの個数に変化を与えないために次数 1 のノードはstパスの数え上げに寄与しない.さらに一般に次数が大きいノードがグラフに存在している方がそのグラフのstパス個数は増加する.これらの要因を考えると東京を中心とするグラフのstパス数が名古屋を中心とするグラフのパス数より小さいことが理解できる.
stパス数え上げ問題ではエッジ数 48 の名古屋を中心とするグラフのstパス数え上げで 12 分以上かかったように多くの計算量と実行時間を必要とする.ここで,stパス数え上げ問題にある制約を課すことでそのstパスの数え上げにおいて実行時間を短くすることを考える.
そこで,stパスに必ずそのパスで通らなければならない中継点を始点終点と同様にランダムに抽出するようなコードを作成し,結果を表にまとめた.
表5:京都を中心としたグラフの経由点の個数ごとの実行時間
| 京都を中心とした大きさ3のグラフの経由点の個数 | 実行時間(s) |
|---|---|
| 個数点が0つの場合 | 31.3842 |
| 個数点が1つの場合 | 24.14 |
| 個数点が2つの場合 | 7.53705 |
| 個数点が3つの場合 | 3.42285 |
| 個数点が4つの場合 | 2.14016 |
表6:名古屋を中心としたグラフの経由点の個数ごとの実行時間
| 名古屋を中心とした大きさ3のグラフの経由点の個数 | 実行時間(s) |
|---|---|
| 個数点が0つの場合 | 436.723 |
| 個数点が1つの場合 | 203.825 |
| 個数点が2つの場合 | 130.637 |
| 個数点が3つの場合 | 35.7585 |
| 個数点が4つの場合 | 33.5933 |
表7:東京を中心としたグラフの経由点の個数ごとの実行時間
| 東京を中心とした大きさ2のグラフの経由点の個数 | 実行時間(s) |
|---|---|
| 個数点が0つの場合 | 226.886 |
| 個数点が1つの場合 | 69.7623 |
| 個数点が2つの場合 | 13.7763 |
| 個数点が3つの場合 | 3.30947 |
| 個数点が4つの場合 | 0.758234 |
上の3つの表を図示すると以下のようである.
図10:各グラフの経由点の個数ごとの実行時間の分布(n =100)(赤が東京,青が京都,緑が名古屋,横軸:経由点の数,縦軸:stパスの数)
このように経由点を増やすことで実行時間が短くなることが見て取れる.
さらに,経由点をさまざまに変化させたときのstパスの個数をviolin plotで図示した.
violin plotとは
Violin plotは、データの分布を視覚化するためのグラフで、箱ひげ図(box plot)とカーネル密度推定(KDE)を組み合わせたものである.データの範囲、四分位範囲、中央値を示す箱ひげ図に加えて、データの分布形状を示すカーネル密度曲線が左右対称に表示される図である.これにより,複数の分布を視覚的に表現できる.

図11:各グラフの経由点の個数ごとのstパスの個数をviolin plotの分布(n=100,Tは東京,Kは京都,Nは名古屋を表し,それに続く数字は経由点の個数を示している.横軸:確率密度,縦軸:stパスの数)
図11の violin plot からわかるように、経由点の個数が増えるにつれて、stパスの分布が次第に狭くなっていく傾向が見られる.これは、経由点の追加がルートの制約を増やし、選択可能なstパスの数を減少させるためである。また、中央値や四分位範囲が縮小していることから、経由点が増えるにつれて、分布の分散が小さくなっていることが確認できる.
特に、都市ごとの比較では、東京 (T) の経由点が多いケースで最も顕著に分布の縮小が見られる.これは、東京の周辺グラフにおいて次数 1 のノードの数が多いため,stパスに大きく影響を与えていることを示唆している.また、名古屋の場合は、特に分布の形状が他の都市と異なり、極端な値を持つ場合が多い.これは,ノード数が京都のグラフよりも多く,次数1のノードが東京のグラフよりも小さいというグラフの特性によるものと考えられる.
今回の研究の反省点と感想
自分自身,クソでかデータを加工して実際に運用するという経験がなかったのでプログラムに適用できるようにデータを加工するまでに非常に時間がかかってしまいました.ただ,この経験から次にまたこのようなデータを扱う機会があれば前よりもスムーズにできると思います.
また,C++での実装の限界を2つの点で感じました.
1つ目に今回の実装において各ノードの情報を全て格納するために二次元の配列を用いたのですが,僕が使っているような雑魚ノーパソのメモリの大きさではすぐに限界が来てしまいました.アルゴリズムを工夫してせっかく実行時間を軽くしたのにメモリの上限で先に進めなくなったのは悔しいです.
本来のフロンティア法の発想ではフロンティアの情報のみを保持していればよく,僕はC++でその実装方法を知らなかったのでメモリ軽減を行えませんでしたが,もし可能な方がいらっしゃいましたらそこの修正を行ったらおもろいんじゃないかと思います.
2つ目に他言語で実装した方々のソースコードと比べ自分のc++でのソースコードは圧倒的に大きくなっていたことです.正直600行以上のソースコードを何個も書くことは非常に疲れるので(競プロerにあるじきことですが)次回からはpythonでの実装を検討します.
ZDDに詳しい方と話してみた
大学の講義で今期 ZDD 分野に詳しい方がおり,その方は日本最北端から日本最南端駅までのパスの個数を ZDD で求めていることを授業中紹介されておりました.そこでどのようなアルゴリズムを使えばそのようなことが行えるか伺ったところ日本は細長い形状なのでその日本の形と垂直にフロンティアを遷移させていけばフロンティアが保持しなければならない情報は小さくなるので後はスパコンで処理をさせればいずれ結果は出力されるとおっしゃってました.確かに,今回の実装は地理的な情報からフロンティアを遷移させるという工夫を行えなかったですし,先ほども述べたように実装上の問題からフロンティア以外の情報も保持してしまっていました.
主な参考文献
https://eprints.lib.hokudai.ac.jp/dspace/bitstream/2115/74087/1/Hirofumi_Suzuki.pdf
https://www.ai-gakkai.or.jp/jsai2016/webprogram/2016/pdf/927.pdf
https://ja.wikipedia.org/wiki/%E4%BA%8C%E5%88%86%E6%B1%BA%E5%AE%9A%E5%9B%B3
https://qiita.com/kpasso1015/items/802885926c41cc8d3132
https://orsj.org/wp-content/corsj/or60-10/or60_10_600.pdf
https://www.ekidata.jp/
https://www.edu.kobe-u.ac.jp/istc-tamlab/cspsat/pdf-open/cspsat2_seminar06_nakamoto.pdf
超高速グラフ列挙アルゴリズム (著:湊真一)