この記事は以下の記事の ZDD を用いたパスカウントについての記事のデータ整理部分の手順を解説した記事である.
https://qiita.com/sunagimo3/items/4f761f293c535fcb85a0
目的
1.駅データ.jpから得られた鉄道網のデータを加工しプログラムで動かせるようにし, 2.またstパスの個数に関係ない駅を削除していくことでデータを縮約する.という2つの目標を目指す.
1.駅データ.jpから得られたデータの加工
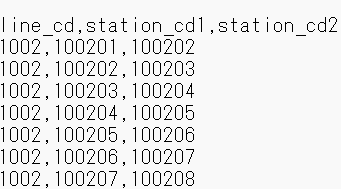
駅データ.jpで活用していくデータは以下2つのデータである.
上のデータは駅データ, 下のデータは接続駅データであり,上の画像はそれぞれデータの上部を切り取った画像である.
このデータの内上のデータで用いる項目はstation_cd,station_g_cdであり,下のデータで用いる項目はstation_cd1,station_cd2である.
station_cdはある路線に存在するある駅の番号であり,station_g_cdある駅の番号である.
例えば,湘南新宿ラインの新宿駅をA,山手線の新宿駅をBとする.
この時,cdにおいてAとBを表す番号は異なるが,g_cdにおいてAとBを表す番号は等しい.この2つのデータから実際にプログラムを動かせるように以下の3ステップで必要なデータを抽出し,加工していく.
1.各データから必要な項目を抽出する
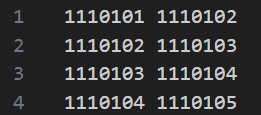
実際に上のデータにおいて必要なデータを抽出するのは~のプログラム,下のデータにおいて必要なデータを抽出するのは~のプログラムで行った. その結果, output4,output1のようにデータを変化させれる.
左,表3:1つ目のデータの加工後 右,表4:2つ目のデータの加工後

|
|
2.路線データをcdからg_cdに変換する
今, 下の駅と駅の接続状態を表現しているデータはstation_cdで表されており, 同じ駅でも路線が異なると異なる駅として値を取ってしまう. よって上のstation_cdとstation_g_cdの対応を示したデータを用いることで,station_cdで表された駅間の接続状態をstation_g_cdで表そうとしたプログラムが~である. その結果, output6のようなデータが得られた.
表5:g_cdで表された接続データ

3.路線データの7桁の番号を0から順に振りなお
さらに, station_g_cdの値はデータをみればわかるように7桁の数字であり, この値をそのままプログラムの入力データで動かすのは問題がある.(例えば, 配列を使いずらくなる) よって, プログラム~により再度0から順番に値を振りなおす. そのデータが以下のoutput7である.
表6:表5の接続データを0から番号を振りなおしたデータ
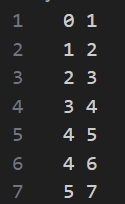
これで日本全国の駅間の接続状況を表現したデータを扱いやすいデータとして得ることができた. (1の操作の達成)
2.またstパスの個数に関係ない駅を削除していくことでデータを縮約する
次に2.stパスの個数に関係ない駅を削除していくことでデータを縮約する操作を行いたい.
今回output7に対して以下の4つの操作により縮約を試みた.
1.連結成分の調査
このグラフの連結状態を調査したところ沖縄エリアに存在する連結成分とそれ以外全ての駅間でなす非常に大きい連結成分が得られた. つまり, 沖縄以外のエリアのグラフにおけるstパスの個数を考えるとき沖縄エリアの鉄道網はstパスに関与しないが沖縄エリアの鉄道データを持つとそれだけ計算量が大きくなるので今回は沖縄エリア以外のグラフを考えることにする.
2.両端が同じエッジの重複の削除
新宿駅と代々木駅をつなぐ鉄道はJR山手線, JR中央総武線, 都営大江戸線が存在するがこれを今回は1つのエッジとしてみなすことにする.(つまり, 今回のstパスは使用した路線が異なっていても通ったノードが同じであるならばそれは同じ経路と判定する.)
3.次数2のノードの削除
次数2のノードは本質的にstパスの個数に変化をもたらさない. これはstパスが次数2のノードを経由する際, 分岐が起き得ないからである. 次数2の削除されたノードの情報はその両端のノードが持つのでグラフの情報に変化はもたらさない.
(次数2ノード削除例)
 図1:次数2のノード削除がされてない状態のグラフ |
ノード4とノード7をつなぐエッジにはノード5,6の情報が内在している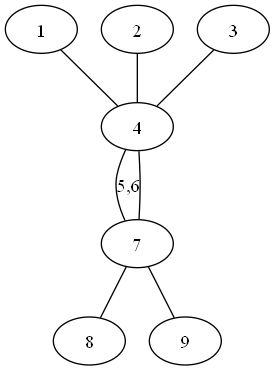 図2:図1のグラフの次数2のノード削除がなされた状態のグラフ |
4. 次数1のノードの削除
次数1のノードは削除対象である. というのも次数1のノードを削除してもそのノードの情報は接続ノードが保持し, かつstパスの個数に変化を及ぼさないからである.
(ノード1の削除例)
 図3:次数1のノードが削除されていないあるグラフ |
ノード4にノード1,2,3の情報が内在しており,ノード7にノード8,9の情報が内在している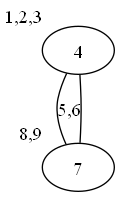 図4:図3のグラフの次数1のノード削除がなされた状態のグラフ |
 図5:次数が2のノードがまだ存在している状態のグラフ |
ノード4に1,2,3,5,6,7,8,9の情報が内在している
 図6:図5のグラフの次数2のノードを削除した後のグラフ |
この後,実際にこのグラフ縮約方法を全国の路線図に適用すると以下のようなグラフが得られた.
図7:縮約しきった後の全国の路線を表現したグラフ.赤が東京駅,青が京都駅,緑が名古屋駅を示している
グラフの縮約操作により,もともと存在した10177個のエッジを持つグラフを1139個のエッジに減少させることができており大幅な縮約ができていることが確認できる.また,縮約をする前のグラフと比較して縮約を完了した次数分布は以下のようになった.
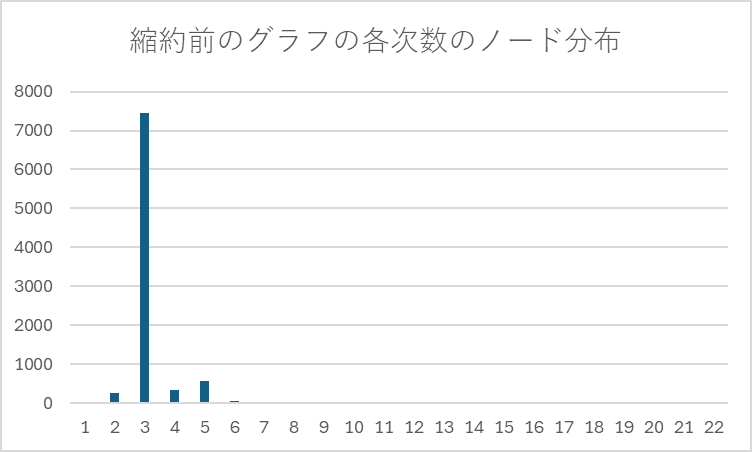 図8:縮約する前のグラフの各次数のノードの数の分布(横軸:次数,縦軸:各次数のノード数) |
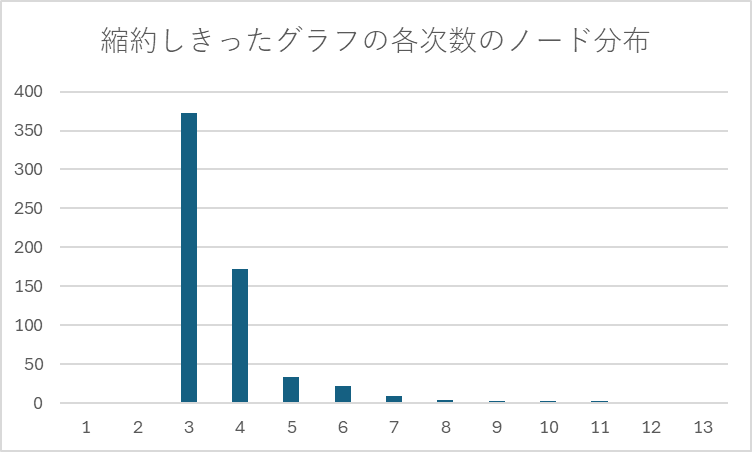 図9:縮約する後のグラフの各次数のノードの数の分布(横軸:次数,縦軸:各次数のノード数) |