この記事は「学生団体 P&D Advent Calendar 2017」の13日目です.
「だって可能性感じたんだ. 」
って感じで, 前期に研究室で学習した内容が いろんなアイディアで使えるのでは? 引き出しがある人が知ったら化けるのでは? と思っているので共有します.
せっかく読んでもらっているので最後まで読んで何かを得てもらいたいので、今回は理論は省いて, "何ができるのか" を知ってもらいたいと思います. (3日前に本研究のガチガチの直系のお弟子さんがQitaに投稿していることもあって)
二分決定木(BDD - Binary Decision Diagram)
これから色々書いていきますが、言いたいことの根幹はここです. もうここだけ見てください.
コンビニにいって, 商品を購入します.
10円の商品a, 30円の商品b, 50円の商品c がそれぞれ一つあります. 合計が50円以上 かつ 80円以内の商品の組み合わせは何通りあるでしょうか?
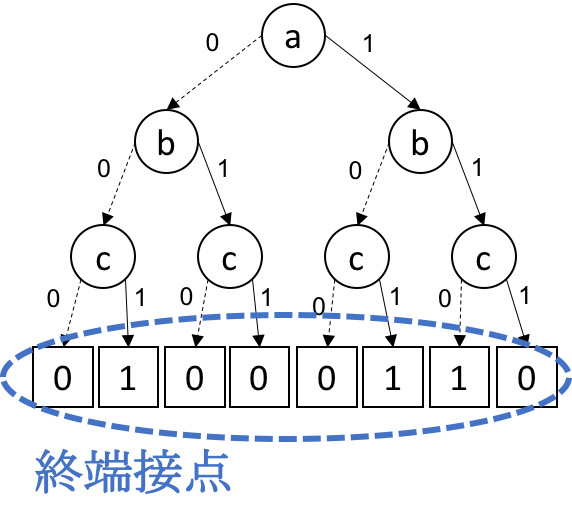
答えは {ab,ac,c} の3通りです. それぞれ合計60円, 80円, 50円. この組み合わせ集合を二部決定木で表現すると次のようになります.
二部決定木では, 一つの階層で 一つのアイテムを使う場合と使わない場合を考えます.
使う場合は1-枝(右側) 使わない場合は(左側)といって分けられます. それを全てのアイテム分繰り返します. 最後に, その組み合わせが存在すれば1-終端接点, 存在しない場合は0-終端接点に接続します.
例えば, 左から二番目の終端接点の1-終端接点がどうつながっているかを見ると, aの0枝 bの0枝 cの1枝からきていることから, これは{c}の組み合わせを表現しています. 次に右から二番目の終端接点の1-終端接点はaの1枝 bの1枝 cの0枝からきているので, {ab}の組み合わせを表現しています.
このBDDという解集合のデータ構造は以下の利点があります。
- 辞書的にcを使う解を索引することができる
- アイテムを一つしか使わない解の検索ができる
- 集合演算を使ってBDDとBDDの和・積なども計算して新しいBDDを作成することもできます.(aを必ず購入するBDDと, 値段が50円以上のBDDの積をとると, aを必ず購入する50円以上のBDDが作成されるということ)
つまり
アイテムの組み合わせ集合を考えるときは, BDDの構造に落とし込むことで, 全ての集合から数え上げることができる.(しかもいいことがたくさんある)
商品って考えるとお固いけど, 5人とかでグループ活動してるときに, この中で僕のことを好きな人の組み合わせは何通りあるんだとか考えるの楽しいですよね. aちゃんだけが僕のことを好きな場合もあるし, bちゃんとc君が実は僕のこと好きじゃない組み合わせも結構あるなぁとか, aもbもcもdも僕のことを好きなパターンあるしうっほほい. ちなみにBDDは下の一番左は全部の0枝がくっついてるってことなので空集合を表します. この妄想では, 空集合が1終端接点につながるパターンは考えないやつですね〜
ただ, お気付きだと思いますが, このBDDのデータ数は アイテムが一つ増えるたびに階層が一つ増えるので, データ数は2倍になってしまいます.
実際の社会では使えない気がしてきました. コンビニの商品の種類の数とかは実在2500種類といわれるそうですし.(つまり 2^2500(2の2500乗). これはあかん. )
その 組合せ爆発 を救うのがZDDです.
ZDD (Zero suppressed BDD)
直訳すると"0を抑制したBDD"です. なんか減らしてくれそう.
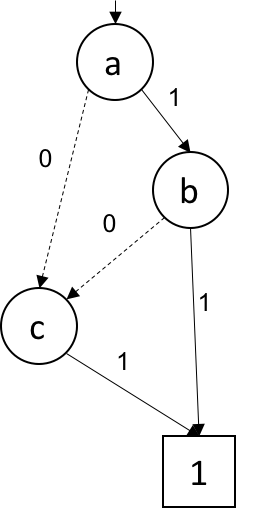
なんか先ほどと比べるとすっきりしたグラフになってますね. でもこれも先ほどのBDDと同じ {ab,ac,c}の集合を表します.
BDDに冗長接点の削除, 等価接点の共有といった操作を行うとこのような図が得られます.
辞書的な索引等のBDDの良いところはそのまま, 同じように組み合わせ集合を表現できます.
BDDからいろんな操作を使ってZDDを得るボトムアップ的なやり方は, 結局一回BDDを作っていますのでそれではあんまり意味がない気がします. なのでトップダウン的にいきなり, ZDDを得るやり方も存在します.
最後にそれを実装するライブラリを紹介して終わります.
TdZdd
なんと, トップダウンでZDDを構築する関数を提供するC++のライブラリTdZddがあります.
こちらのほうが次にあげるGraphillionよりも汎用性があります.
Graphillion
Graphillionが解決してくれる問題としてよく取り上げられるのが"お姉さんの問題"です.
ちょっと昔にTwitterでバズったやつですね.
動画の中では俗に言うs-t経路問題を解こうとしています. お姉さんは辺にそれぞれidを与え最初のBDDのときのように数え上げをおこなっています. (厳密にはただBDDをつくっているよりかはもっとよいアルゴリズムでお姉さんは頑張ってるらしい) 1・1の格子グラフのときはわずか辺の数は4本ですが, 2・2のときは12本, 3・3のときは24本, 4・4のときは40本...n・nのときは n*(n+1)*2本です. 2^(辺の数)なので, それは確かに組み合わせ爆発しますね...
Graphillionはグラフに関する様々な最適問題をとくためのPythonライブラリです. ZDDを効率よく構築するフロンティア法を実装しています.
次の動画で, お姉さんを救うだけでなく, 経路の中継地点の設定など複雑なことを実装していることが確認できます.
まとめ
BDDは組み合わせ集合を考えるときにすごく役に立つ.
ZDDはBDDのいいとこどりしたもの.
TdZddはZDDをつくってくれる関数を提供するC++のライブラリ.
Graphillionはグラフ関係のZDDをつくってくれるPythonのライブラリ.
組み合わせ集合ってのが何に使えるのか私のアイディアだと,
自分がもっている服のコーディーネートの全列挙とか....()
私はこのGraphillionを使ってあるボードゲームの解析をおこないました.
それはまたいつかの機会に.
参考文献
-
超高速グラフ列挙アルゴリズム
https://www.morikita.co.jp/books/book/2838 -
クヌース本7.1.4 二分決定図