1. はじめに
大学で機械学習を勉強しており、NEAT(NeuroEvolution of Augmenting Topologies)の論文を読む機会があったのでNEAT-PythonのリンクにあったCodeReclaimersさんのコードをお借りしてNEATをpython3で実装しました。コードが長いので全5回に分けてコードを紹介していきます。
自分で理解するときはかなり苦戦したので、同じような方がいるかもしれないということで投稿に至りました。何か誤りを見つけた際はコメントいただけると幸いです。
CodeReclaimersさんのコードの中でも今回は論文にもあった排他的論理和(XOR)に挑戦しました。
排他的論理和とは2つの入力(Input)のどちらか片方が真でもう片方が偽の時には結果(Output)が真となり、両方とも真あるいは両方とも偽の時は偽となる演算のことを指します。今回は0を偽、1を真としています。
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2. 環境
Anaconda3(Python3)
3. NEATとは
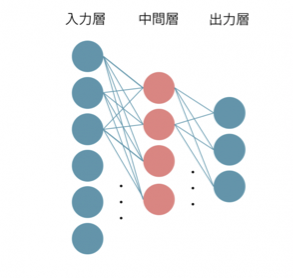
NEATはNE(NeuroEvolution)という強化学習の一種で、論文によると当時(2000年ごろ)の一般的なNEは入力層及び中間層、出力層間の結合を固定し、結合の重みづけを変えることで出力層で得られる結果の精度を上げることができました。この際、中間層は単一の層した存在せず、隠れ層の一つのノードが全ての入力層及び出力層のノードに繋がっているので、結合の重みづけを変更することのみでしか出力結果の精度を上げることができませんでした。
さらに、結合を変えることによって重みづけだけではなく、ネットワーク構造によってもその精度を上げる動きがあり、TWEANNs(Topology and Weight Evolving Artificial Neural Networks)という重みづけとネットワーク構造の両方に着目して出力の精度を上げる方法が生まれました。
NEATはこのTWEANNsの弱点をいくらか補う形で誕生した手法で、以下の点でNEATは他の手法と異なるそうです。
・与えられたノードをそれ固有のものにする(ネットワークの消滅を防ぐため)
・ネットワークを種に分ける(突然変異によるネットワークの衰退を防ぐ)
・初期状態が最もシンプルなネットワーク構造をしている
もっとちゃんと教えてくれ!という場合はを【わかりやすく解説!】NEATとは?その誕生とその後に迫る!ご覧ください!
必要となる前提知識
実装の前に基本な考えを整理したいと思います。NEATは生物の進化の流れを根底の概念としてもつので、この章では後で実装するpythonコードを、随所に生物単語を用いて説明します。次の章で実際のコードを紹介するので面倒な方は飛ばしていただいても構いません。
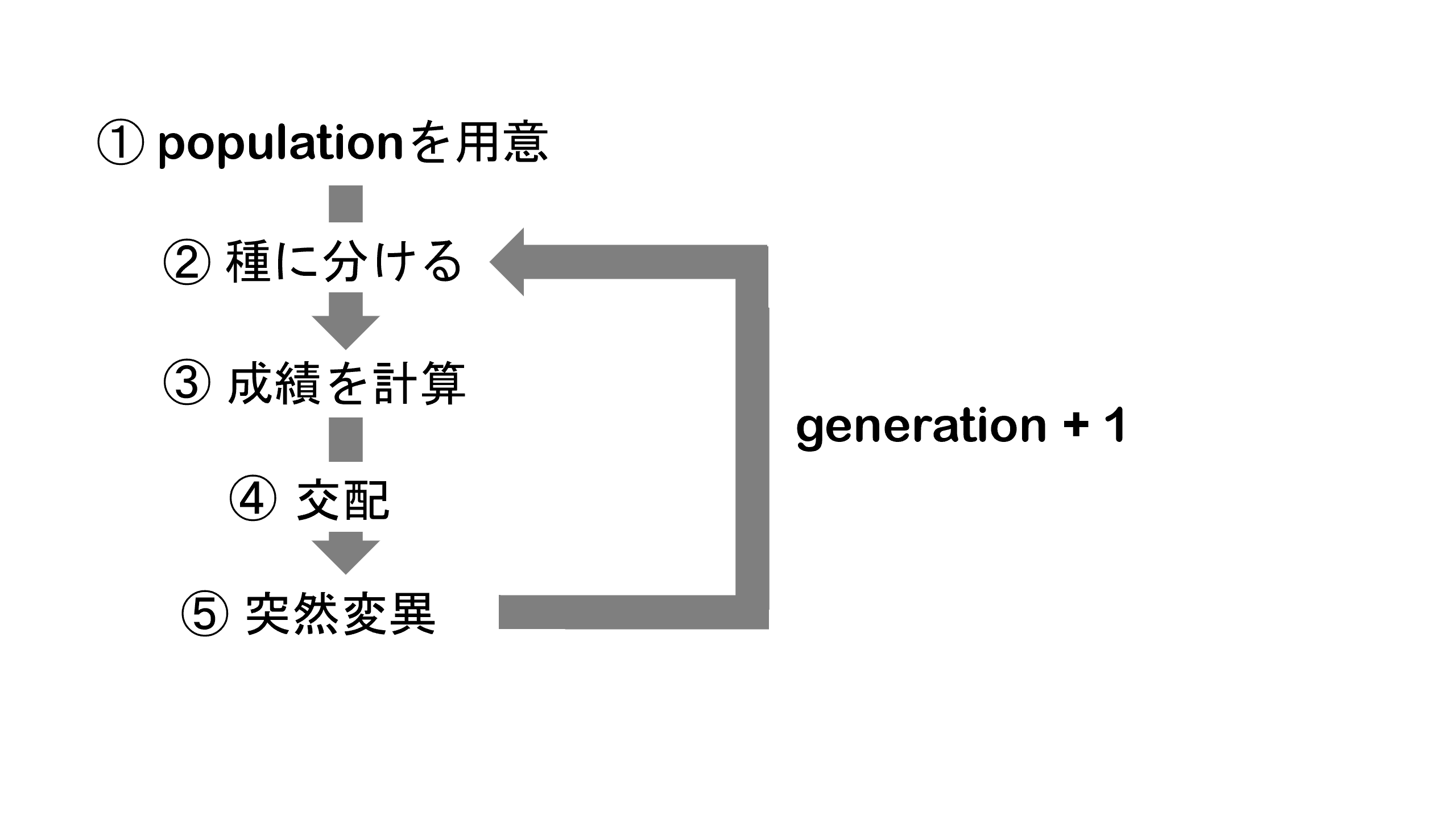
はじめに初期状態を用意して、種に分けます。次に成績の計算をさせて、成績が優秀な上位20%をランダムに交配させて次の世代を作ります。この際に突然変異を起こさせ、子供のネットワーク構造や重みづけを親のそれと少し変化させます。そしてまた種に分けて成績の計算をさせて、、とこの流れを繰り返して出力精度を上げます。第0世代(generation=0)を最初の初期状態から次の子供を作るまでとし、世代を重ねます。
初期状態
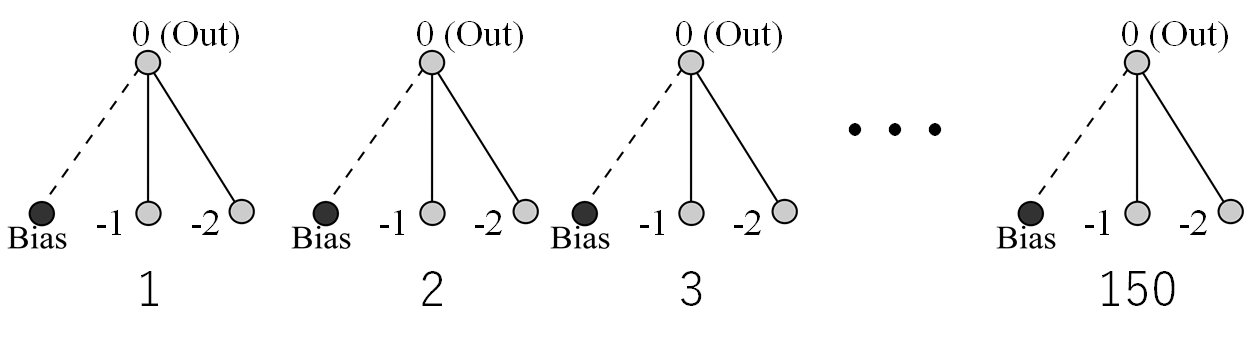
初期状態というのは、下図にあるようなネットワークが150体用意された状態のことを指します(おそらく何体でも良いみたいですがここでは論文に従うことにしました)。
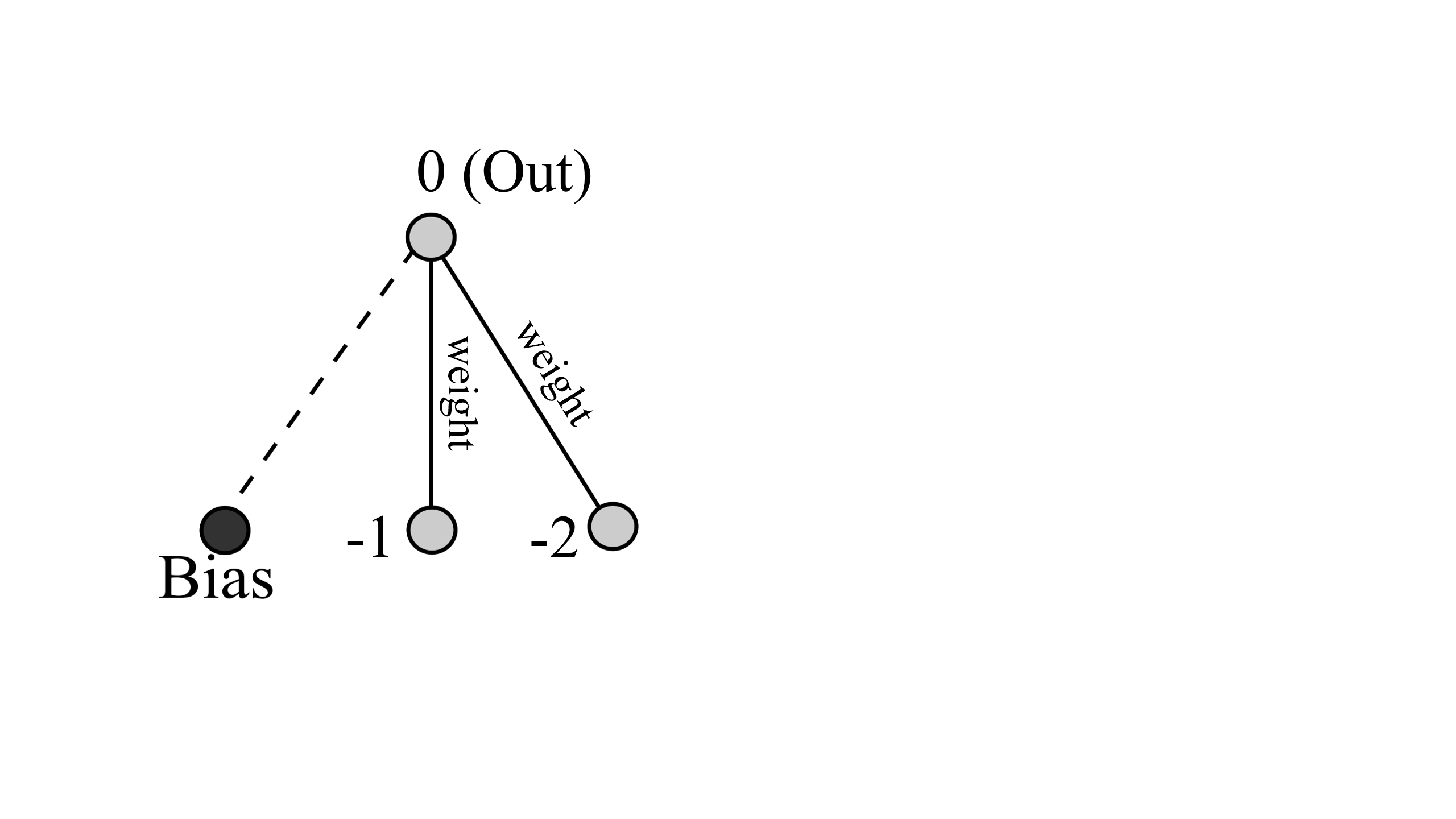
-1、-2が入力層でOutが出力層、Biasは入力層以外のどのノードにも結合することができるらしいです。NEATは初期設定として最もシンプルなネットワークなので中間層は用意しません。また、-1とOutを結ぶ結合、-2とOutを結ぶ結合にそれぞれ重みづけ(weight)がされており、最終的なOut(出力層)の値は
$$out=f(Bias+Inupt(-1)\times weight+Inupt(-2)\times weight)$$
で表現することができます。fはsigmoid関数とします。
例えばInuptが0,0の場合は
\begin{align}
out &= f(Bias+0\times weight+0\times weight) \\
&= f(Bias)
\end{align}
となります。また、Biasとweightは平均0、標準偏差1の正規分布に従ったランダムな値として設定しておきます。
種に分ける
この状態でネットワークをグループ(以降は種)に分けるのですが、最初はネットワーク構造が全て同じなので種が分かれることはあまりありません。世代を重ねると150体のネットワーク構造に多様性が生まれ、構造が似ていないもの同士は別の種に分類されるというわけです。
種に分けることは、後に起こる突然変異によって変化したネットワークを衰退させないために行うそうです。
成績を計算
次にそれぞれのネットワークに成績の計算をさせます。成績とはどれだけ理想のOutputを出力したかを表し、outputの結果を元に計算します。排他的論理和は4つの組があり、二つのInputに対して、一つのOutputを計算するので、合計で4つのOutputが計算され、その値で成績が決まリます。ここでは排他的論理和を考えているので、Inputが0,0であればOutputが0に近い方が成績が高く、0から離れれば離れるほど成績が悪いということです(Inputが0,1であればOutputが1に近い方が成績が高く、1から離れれば離れるほど成績が悪い)。
第0世代はこの150体は全て同じネットワーク構造をしていますが、Biasと二つのweightが異なるのでそれぞれのネットワークが最終的に出力する値は異なります。
交配
成績が上位20%のネットワークを親としてこの集団からランダムに交配させて子供を作ります。成績が上位の親のみを交配させることで子供は親世代より少しだけ成績が全体的に上がります。また、これに突然変異の影響が加わり、子供世代は多様性が広がり、種が分かれやすくなります。
そして次の世代以降、同じ流れが繰り返されます。最後はある世代のあるネットワークの成績がある水準を超えたら計算が終了します。
次は実際の実装に移ります。
4. NEAT 実装
実装の概要
このような手順で実装を行います。
コード
最初はpopulationを用意します。
populationの用意(①)
from itertools import count
num_inputs = 2
num_outputs = 1
class DefaultGenome(object):
def __init__(self, key):
self.key = key
self.connections = {}
self.nodes = {}
self.fitness = None
self.node_indexer = None
def create_new(genome_type, num_genomes):
new_genomes = {}
genome_indexer = count(1)
output_keys = [i for i in range(num_outputs)]
for i in range(num_genomes):
key = next(genome_indexer)
g = genome_type(key)
for node_key in output_keys:
g.nodes[node_key] = DefaultGenome.create_node( node_key)
for input_id, output_id in DefaultGenome.compute_full_connections(g):
connection = DefaultGenome.create_connection(input_id, output_id)
g.connections[connection.key] = connection
new_genomes[key] = g
return new_genomes
def create_node(node_id):
node = DefaultNodeGene(node_id)
node.init_attributes()
return node
def compute_full_connections( g):
output_keys = [i for i in range(num_outputs)]
input_keys = [-i - 1 for i in range(num_inputs)]
connections = []
for input_id in input_keys:
for output_id in output_keys:
connections.append((input_id, output_id))
return connections
def create_connection(input_id, output_id):
connection = DefaultConnectionGene((input_id, output_id))
connection.init_attributes()
return connection
def size(self):
num_enabled_connections = sum([1 for cg in self.connections.values() if cg.enabled])
return len(self.nodes), num_enabled_connections
def __str__(self):
s = "Key: {0}\nFitness: {1}\nNodes:".format(self.key, self.fitness)
for k, ng in self.nodes.items():
s += "\n\t{0} {1!s}".format(k, ng)
s += "\nConnections:"
connections = list(self.connections.values())
connections.sort()
for c in connections:
s += "\n\t" + str(c)
return s
from random import random,gauss
compatibility_weight_coefficient = 0.5
class BaseGene(object):
def __init__(self, key):
self.key = key
def __str__(self):
attrib = ['key'] + [a for a in self._gene_attributes]
attrib = ['{0}={1}'.format(a, getattr(self, a)) for a in attrib]
return '{0}({1})'.format(self.__class__.__name__, ", ".join(attrib))
def __lt__(self, other):
return self.key < other.key
def mutate(self):
for a in self._gene_attributes:
from random import random
v = getattr(self, a)
if a == 'enabled':
r = random()
if r < 0.01:
v = random() < 0.5
setattr(self, a, v)
else:
r = random()
if r < 0.75:
v = v + gauss(0.0, 0.5)
else:
if r < 0.1 + 0.75:
v = gauss(0, 1)
setattr(self, a, v)
def copy(self):
new_gene = self.__class__(self.key)
for a in self._gene_attributes:
setattr(new_gene, a, getattr(self, a))
return new_gene
def crossover(self, gene2):
new_gene = self.__class__(self.key)
for a in self._gene_attributes:
from random import random
if random() > 0.5:
setattr(new_gene, a, getattr(self, a))
else:
setattr(new_gene, a, getattr(gene2, a))
return new_gene
class DefaultNodeGene(BaseGene):
_gene_attributes = ['bias']
def __init__(self, key):
BaseGene.__init__(self, key)
def init_attributes(self):
self.bias=gauss(0, 1)
def distance(self, other):
d = abs(self.bias - other.bias)
return d * compatibility_weight_coefficient
class DefaultConnectionGene(BaseGene):
_gene_attributes = ['weight', 'enabled']
def __init__(self, key):
BaseGene.__init__(self, key)
def init_attributes(self):
self.weight=gauss(0, 1)
self.enabled=True
def distance(self, other):
d = abs(self.weight - other.weight)
if self.enabled != other.enabled:
d += 1.0
return d * compatibility_weight_coefficient
そしてpopulationを定義します。
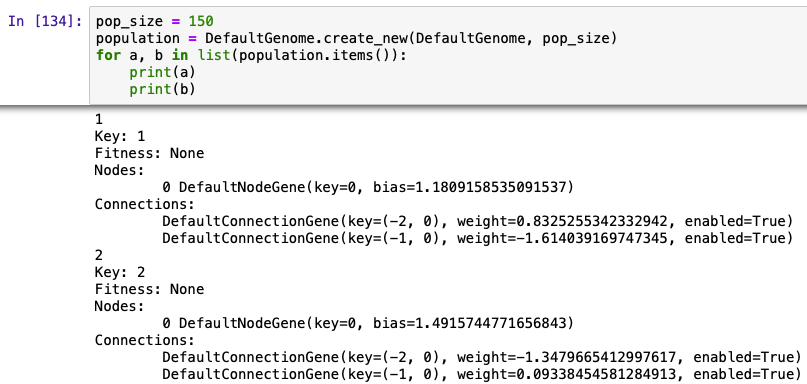
pop_size = 150
population = DefaultGenome.create_new(DefaultGenome, pop_size)
for a, b in list(population.items()):
print(a)
print(b)
できたpopulationは辞書型なので、items()というメソッドを使用してpopulationの各要素をkey(a)とvalue(b)に分けています。
実行結果をみると、それぞれのネットワークはKey, Fitness, Nodes, Connectionsに分かれています。このような表示になるのは、DefaultGenomeクラスの下の方にあるstrという特殊メソッドがあるためです。
Nodesをみると、DefaultNodeGeneが定義されており、その中にさらにkeyとbiasが与えられています。
Connectionsをみるとkey, weight, enabledがそれぞれ与えられています。ここで出てくるenabledはTrueまたはFalseをとる変数で、Trueの場合はそのDefaultConnectionGeneが有効であることを表し、ネットワークを構成するConnectionsとして機能することができます。逆にFalseの場合はConnectionsとして機能することができません。
enabledは成績を計算する際に考慮に入れます。
次回は今回用意したpopulationを種に分ける操作を行います。