#はじめに
大学で機械学習を勉強しており、NEAT(NeuroEvolution of Augmenting Topologies)の論文を読む機会があったのでNEATがどういうものか、また誕生した経緯とその後現在までどのような発展を遂げたのかを調べました!
NEATは強化学習の一種で、このアルゴリズムを使うことによって動画のように、車(ターゲット)を周りの環境(壁)に合わせて適応すること(運転)を学習させることができます!
(動画はTomek Sさんのものをお借りしました、Car learns to drive - NeuroEvolution of Augmented Topologies (NEAT) for a 3D car made in Unity)
この記事ではNEATという手法によってどのようにターゲットを強化するかを説明しています。また、より実践的に学ぶために人工ニューラルネットワーク(動画の右上にある赤緑黒の線のやつ)についても説明します。
【対象とする読者】
・NEATというものに出会ったけど意味がわからん!
・コンピュータサイエンス入門者だけど、NEATのことをじっくり勉強したい!
#NEATとは?
まずイメージを掴んでいただくためにざっくりとその手法について説明します。NEATは2002年の論文で初めて発表された強化学習の手法で、最適化問題を対象としています。ここでいう最適化問題とは与えられた条件の下で最もパフォーマンスを高くする最適な解を求めることを指します。
例えば、あなたが泥棒になって誰かの家に侵入したと考えてみてください。家には次の金品がありました。
||No.1 |No.2 |No.3 |No.4 |
|:-:|:-:|:-:|:-:|:-:|:-:|
|g |600 |400 |200 |100 |
|¥ |2500 |2000 |1200 |1800 |
カバンには合計で1000gの金品を入れることができます。
最もお金の価値が高い金品を持って帰りたいと考えていたあなたは、No.1とNo.3、No.4を持ち帰ればいいことに気が付きます。
||No.1 |No.3 |No.4 |合計 |
|:-:|:-:|:-:|:-:|:-:|:-:|
|g |600 |200 |100 |900 |
|¥ |2500 |1200 |1800 |5500 |
この例では「1000g入るカバンにどの金品を入れれば最もお金の価値が高いか」という最適化問題に対して、「No.1とNo.3、No.4の金品」という最適解が求められました。
このような少ない組み合わせを考える際は問題ないのですが、次にような例では自力で考えることは難しくなります。
||No.1 |No.2 |No.3 |No.4 |No.5 |No.6 |No.7 |No.8 |
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|g |200 |140 |300 |170 |100 |160 |220 |200 |
|¥ |2500 |2000 |1800 |1200 |1800 |2500 |2000 |1500 |
このような場合に、NEATのような手法が役たちます。この例では、「No.1、No.2、No.4、No.5、No.6、No.7」が最適解となります。(金額は¥12000)
NEATは自力で最適解を求められない場合にとても有効な手段となります!次はNEATの手法についてそのイメージをお伝えします。
###■まずはイメージから
NEATは最適化問題を生物が進化する際の自然淘汰や、交配、変異といった考えをうまく取り入れて計算をしています!
ここで、先ほどの最適化問題をNEATを用いて再び考えます。「ある家に侵入して金品を盗む」というミッションです。また、目標金額は¥5000とします。
NEATは初め能力の違う5人(A~E)を用意しました。この時点で、どんな家の間取りか、どんな金品があるかはわかっていないので5人の能力はまだ未知数です。それぞれを強盗に行かせ、合計何円の金品を持ち出すことができたかでその人の能力を測ります。
その結果、次のようになりました。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| ¥ | 1000 | 1500 | 900 | 2000 | 600 |
どの人も¥5000には遠く及ばず、5人の中ではDが最もパフォーマンスがよく、Eが最も悪くなりました。そこでNEATは成績が悪い下2人を解雇して(自然淘汰)より能力の高い3人をランダムに交配させます。
そして子供の世代として再び5人の泥棒が生まれました。それぞれの親は親世代の中で比較的パフォーマンスが高かったので、平均的なパフォーマンスは高くなっているはずです。さらに子供たちは、親が交配した際に起こる変異の影響も受けます。この変異はランダムなのでパフォーマンスがさらによくなるかもしれないし、悪くなるかもしれないです。親たちには現役を引退していただいて、子供たちが再び泥棒をしました。
その結果、次のようになりました。
| a | b | c | d | e | |
|---|---|---|---|---|---|
| ¥ | 1600 | 3000 | 1900 | 1000 | 2600 |
子供世代はbが最もよく、dが最も悪いです。子供たちは進化したことから、先ほどの親世代と比べるとdでさえ親世代の600よりはかなりよくなりました。
しかし、NEATの目標とする¥5000にはまだ及ばず今度は孫世代をつくります。先ほどと同じように下2人を解雇して(自然淘汰)、残った3人を交配させます。孫世代が泥棒をした結果次のようになりました。
| aa | bb | cc | dd | ee | |
|---|---|---|---|---|---|
| ¥ | 5100 | 4000 | 4400 | 4500 | 3900 |
今度は大幅にパフォーマンスが向上し、aaは目標とする¥5000を達成することができました!これで三世代に渡るミッションはついにコンプリートです。
長くなってしまいましたが、NEATのイメージを掴んでいただけたでしょうか!自然淘汰、交配、変異という工程を繰り返すことで泥棒たちは能力を上げることができたのです!
しかし、ここまで理解はできても、より実践的に使うにはまだ物足りない気がします!そこで、次は別の例を使ってもう少し実践的に考えたいと思います。そうすれば他の論文などに触れた際に困ることは少なくなるはずです。
###■人工ニューラルネットワーク(ANN)
先ほどは人を使って金品を盗みましたが、今度は**人工ニューラルネットワーク(Artificial Neural Networks, ANN)**なるものを使います。次の図をご覧ください。

これがANNです。先ほどの車の動画にあったANNよりだいぶシンプルです。これが一番基本の形になります。丸(○)のことをノード、線(-)をコネクションといいます。
下の段にあるノードをInputs(入力)、上の段にあるノードをOutput(出力)といい、Inputsに情報を入力することでOutputでその結果がわかります。また、コネクションの近くにある数字(1, -1)はパラメータでノード同士を繋ぐ重み付けのことを指します。
ここで、x, yに任意の数を代入してzを求めます。今回はzが5以上になればミッションクリアとすると、重み付けがそれぞれ1, -1となっているのでzは、
\begin{align}
z &= x\times 1+y\times (-1) \\
&= x-y
\end{align}
と求めることができます。
上にある一見難しいそうなANNをただの方程式に変えることができました!あれ、案外いけるかも!?
NEATの場合、実際にはこのzにさらに活性化関数というのをかけてOutputとしますが、ここはあくまで概念を理解することに重点を置いているので活性化関数のことは割愛します。
もう一つANNを紹介させてください。次に説明するANNは中間層(hidden)が存在します!

歴史的には、この中間層のおかげでさらに多くの最適化問題が解けるようになりました。例えば、排他的論理和(XOR)です。ここでは深く触れませんが、中間層の存在はとても大きいです!(単純パーセプトロンの仕組みとPythonによる実装をチェックがわかりやすいと思いました)
この場合、zは次のように求めます。
\begin{align}
z &= 2(x\times 1+y\times (-1)) \\
&=2(x-y) \\
\end{align}
これで準備は整いました!このようなANNが先ほどの泥棒の例のようにパフォーマンスを競います。次はANNを用いてNEATを考えます。
###■ANNを使ってNEATを考える
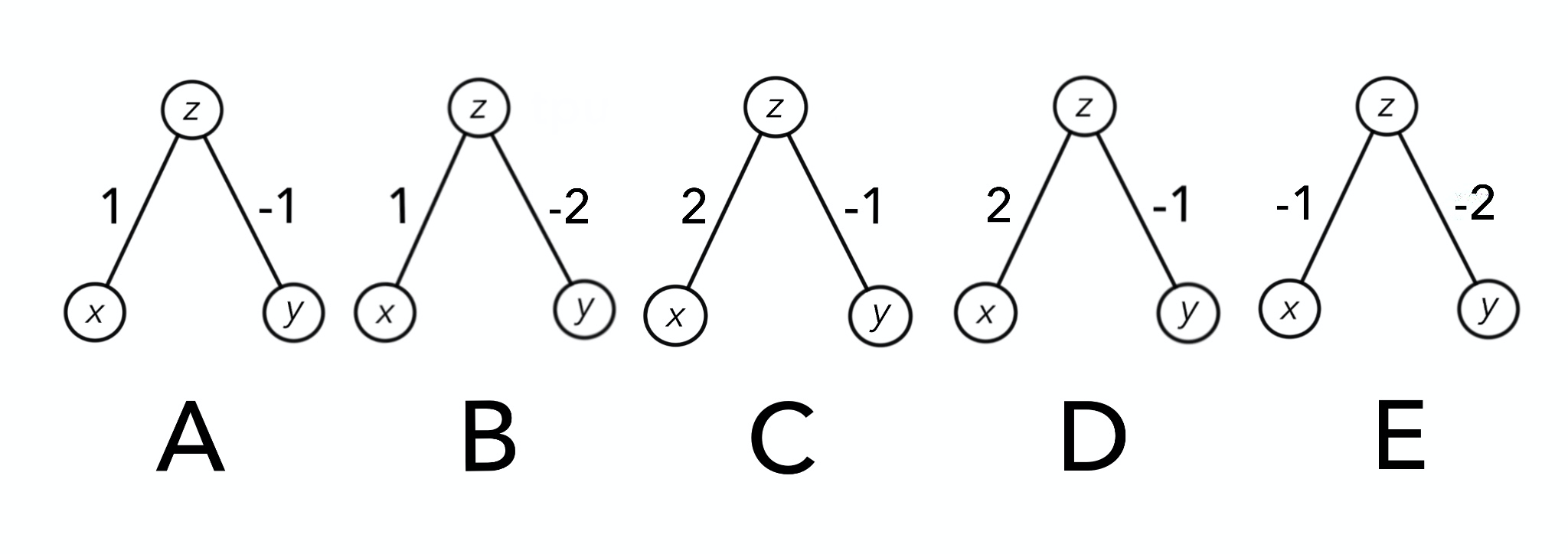
NEATは「zを5以上にする」というミッションの下、初期状態として次のANNを五体用意しました。実際は、五体で済むようなことはなく100とか1000くらい用意するのですが、ここではわかりやすさを優先するためにあえて少なくします。ここではそれぞれ重み付けの値が異なります。また、NEATは初期状態として単純なANNを用いるという特徴があるので全て中間層はまだありません。中間層は変異によってのみ現れます。
どのANNも条件は同じとするので、ここでは全て、入力を(1, 1)とします。つまり、(x, y)=(1, 1)です。この五体のANNにInputs(1, 1)を入力すると、結果は以下のようになりました。
| A | B | C | D | E |
|---|---|---|---|---|
| 0 | -1 | 1 | 3 | -3 |
B、Eがパフォーマンス悪いですね。自然淘汰によってB, Eが除外され、残ったA, C, Dが親となり交配します。例えばA, Cが交配すると、次のようになります。
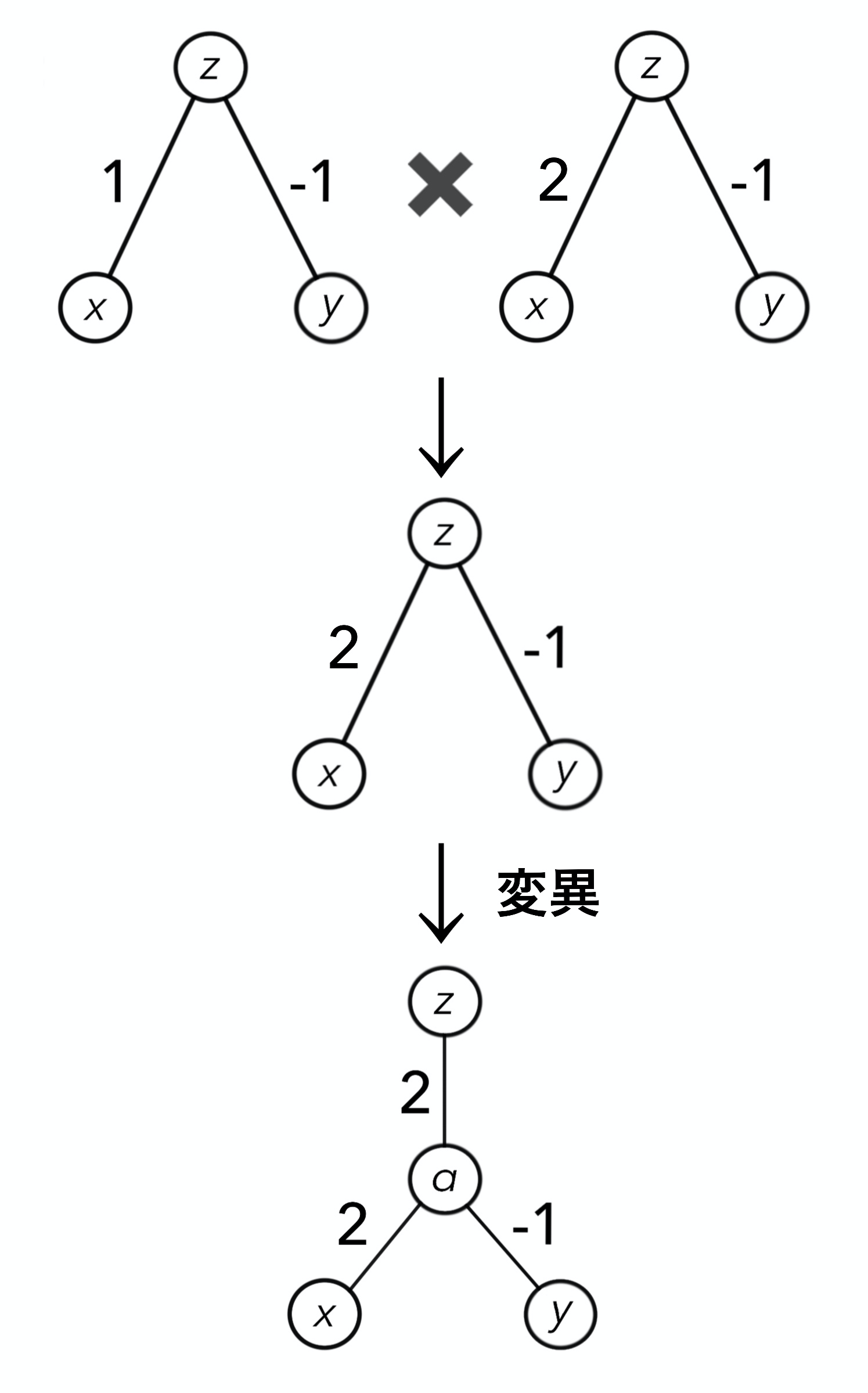
最初、子供のz-x間の重み付けは親のz-x間の重み付けからランダムに決定されます。z-yに関しても同様です。さらに、その後変異を受けます。今回はたまたま中間層が現れました。中間層から出力を結ぶ重み付け(α-z)もランダムに決まります。
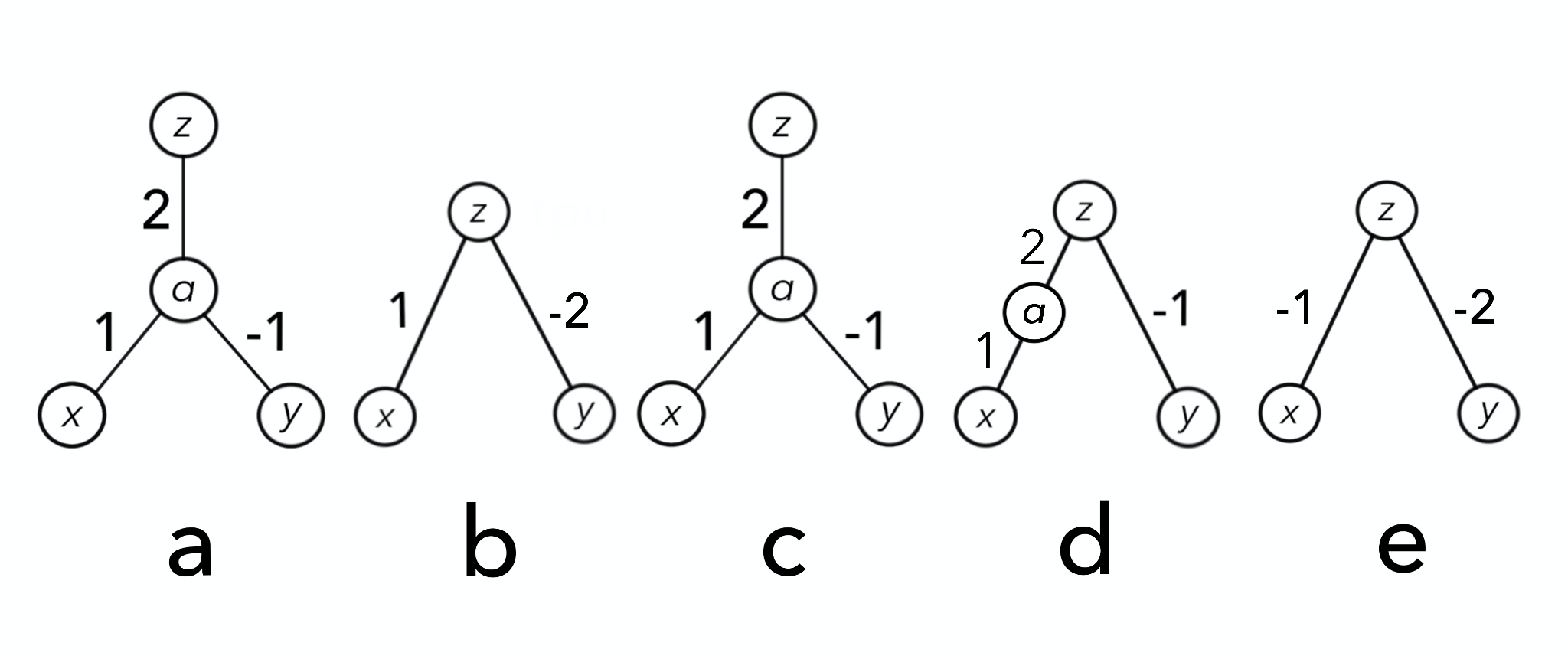
交配の結果、子供世代は次のようになりました。
親世代と比べるとそれぞれの形がより複雑になっていることがわかります。生物多様性という言葉があるように、多様性がパフォーマンスを向上させることからNEATは種という考えも取り入れています。(「NEATの歴史」のところでまた取り上げます)
子供世代のパフォーマンスは次のようになりました。
| a | b | c | d | e |
|---|---|---|---|---|
| 2 | 2 | 2 | 0 | 0 |
a, b, cが2、残りが0と今回はきっぱりと分かれました。先ほどのように自然淘汰、交配、変異によって同様の過程を、zが5を超えるまで繰り返します。
何世代かを経てついにzが5を超えるANNが登場しました。
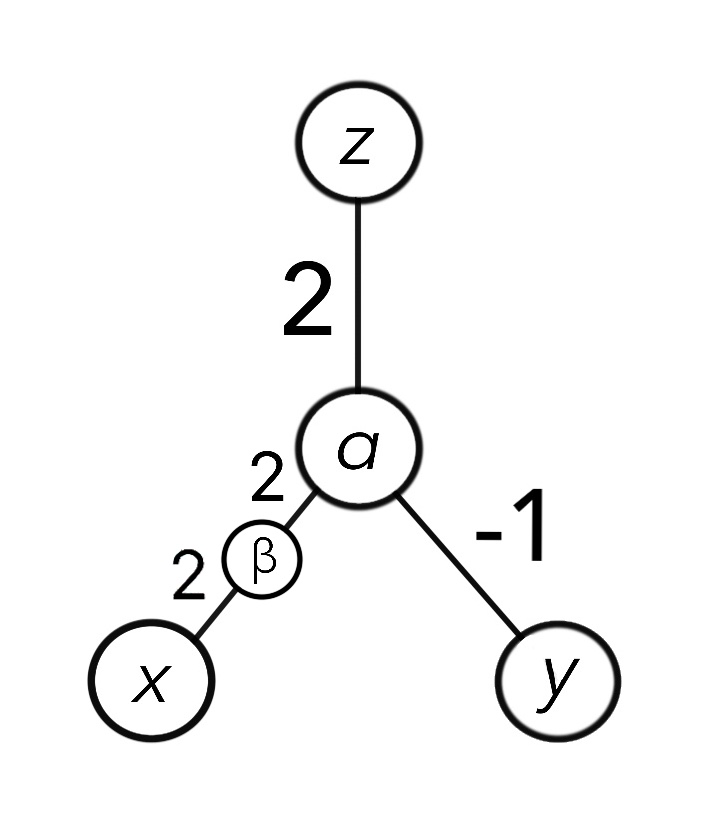
zを計算すると、
\begin{align}
z &= 2(x\times (2\times 2)+y\times (-1)) \\
&= 2(x\times 4+y\times (-1)) \\
&=2(4x-y) \\
&=2(4\times 1-y\times 1) \\
&=6
\end{align}
確かに5を超えましたね。
こんな感じでやっと!!NEATの概要を終わります。ここまで読んで下さり本当にありがとうございます!何か少しでもプラスになればとても嬉しいです!![]()
最初は泥棒を例として簡単に、次に実際に使われているANNを用いてNEATという手法についてみていきました。早速NEATの歴史に入りたいのですが、その前にまだ大事なことがありまして、笑
実は、NEATの中核をなす「生物の進化の考え」はNEATの手法を考えた際に誕生したものではなく、**遺伝的アルゴリズム(genetic algorithm, GA)**という1960年代から続く考えを使用しています。なのでNEATの歴史に触れる前にGAの歴史にも触れておきたいなということです。なので、もうNEATの歴史だけでいいってば!という場合は次の「GAの歴史」は飛ばしてください!![]()
ここで、NEATと遺伝的アルゴリズムは何が違うのかという疑問が生まれるかもしれませんが、NEATにしかない大事な特徴がちゃんとあります(後述)。編集上は「NEATとは?」のところでNEAT固有の特徴を説明するべきなのですが、NEATが誕生した歴史と共に説明した方がわかりやすいと判断したので、「NEATの歴史」のところに記載しました。
次のパートで遺伝的アルゴリズムの大まかな歴史、NEATの歴史、NEATの特徴を説明します。
#歴史
NEATは遺伝的アルゴリズム(genetic algorithm, GA)の考えを基にした手法なので、まずはGAについてみていきたいと思います。
####■遺伝的アルゴリズム(GA)
GAの考えを生み出したのはアメリカのJohn H Hollandと言われています。余談ですが、Hollandは2015年にがんで亡くなりました(86才)。
彼は時代に先駆けて計算科学の分野に入り(1960年代)、GAの考えを生み出しました。1950年代、大学院生だったHollandは複雑系(脳の神経ネットワーク、蜂の巣、気象現象など)の適応システムについて研究していました。適応システムとは、周りの環境の変化に合わせてうまく適応するシステムということです。
以前からコンピュータに触れていた彼はコンピュータで適応システムの研究ができないかと考えはじめ、そこに生物の進化という要素を取り入れました(ここがすごい!)。つまりコンピュータ上で、ターゲットを交配、変異させることで環境に適応させることはできないかと考えたのです。この考えを1975年に遺伝的アルゴリズムとして発表してからその可能性に多くの研究者が気付き、今では様々な分野で応用されています。
####■NEAT
1990年代、アメリカの大学院生だったKenneth O. Stanleyは脳の現象をコンピュータ上で再現することに魅了され、Neuroevolutionの分野に入ります(Neuroevolutionの一分野はGA)。当時そこではすでにいくつかの優れた手法がありましたが、その大部分はコネクションを固定したANNでした。「ANNを使ってNEATを考える」にあったようなANNではなく、交配しても重み付けの値のみが変化するANNだったのです!
そこでStanleyはコネクションも変化させることができれば、理想とする「脳の現象をコンピュータ上で再現」することに近くかもしれないということで、すでにTWEANNsという、重み付けとコネクションを変化させる手法を研究します。この手法の問題点を解決する形で生まれたのがNEATでした。
NEATは次の3点でTWEAANsより優れていると考えられています。
・history marking
・speciate(種)
・simple initial population
「NEATとは?」の例に出てきたような少ないANN数ではこれらの特徴による効果を実感することはできません。(なので、「NEATとは?」で説明せず、ここにしました)
最初のhistory markingはいわば通し番号のようなものです。「ANNを使ってNEATを考える」の例にもあったように新たに出現したノード(中間層)に固有の通し番号を付けます。そうすることによって交配を問題なく行うことができるそうです。もし通し番号を付けなければパフォーマンスを向上するために必要だったかもしれないノードまたはコネクションが無くなってしまいます。このせいで目標とするパフォーマンスに到達する可能性が下がります!
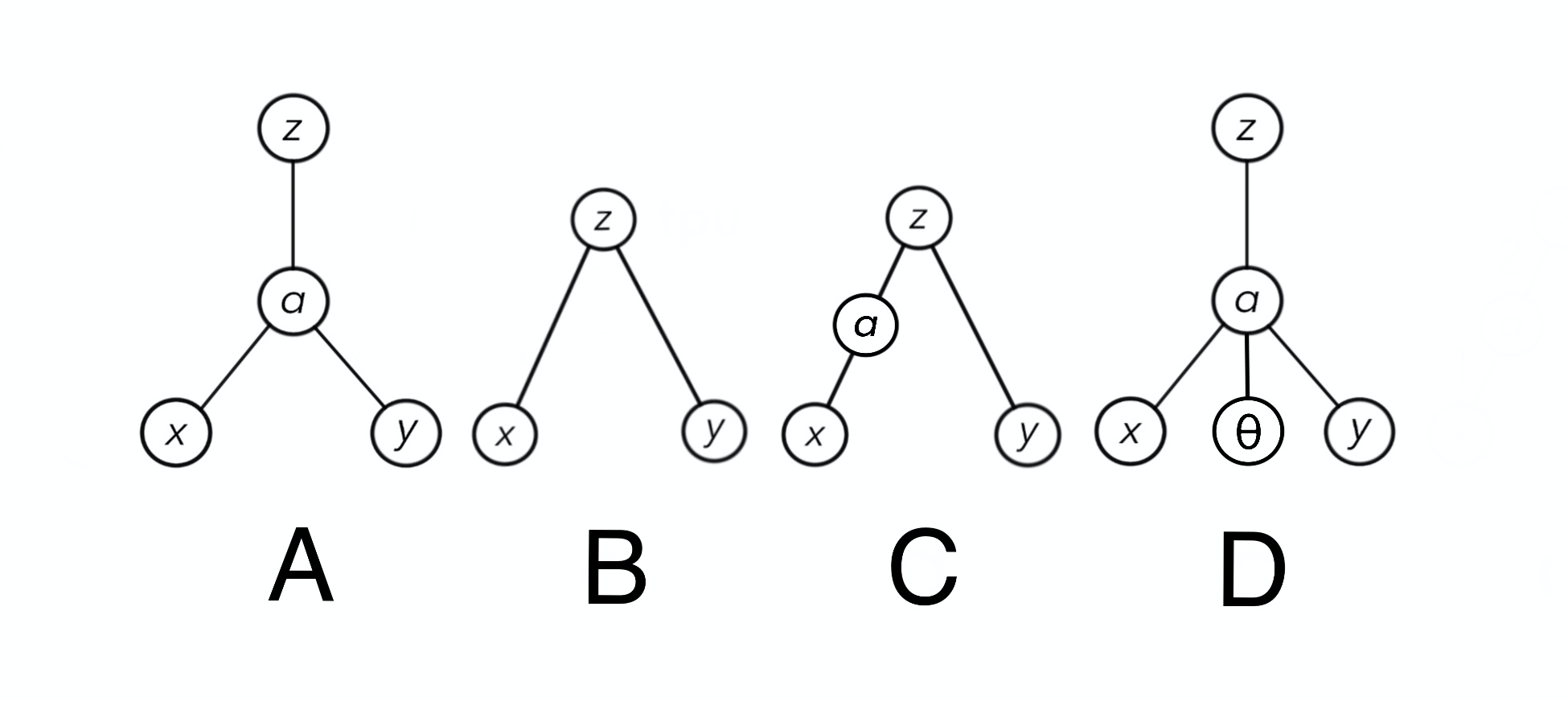
次のspeciate(種)は「ANNを使ってNEATを考える」の生物多様性の部分で触れたものです。NEATはANNたちを種に分けることで変異の要素をなるべく維持するためにあるそうです。もう少し種についてみたいと思います。種に分けるとはいわばグループに分けるようなもので、似ているもの同士を同じ種(グループ)としてまとめます。どのようにして似ているかを区別するかというと、次のように、ノードの数とコネクションの本数に応じて近親(同じグループ)かそうでないかを判定します。
それぞれのノードの個数、コネクションの本数は次のようになります。
| A | B | C | D | |
|---|---|---|---|---|
| Nodes | 4 | 3 | 4 | 5 |
| Connections | 3 | 2 | 3 | 4 |
| 合計 | 7 | 5 | 7 | 9 |
この結果をみると、AとCは同じ種としてグループ化し、B、Dはそれぞれ別の種として独立します。つまり全部で3種いるということになります。本来ならもう少し細かなパラメータも調整して種に分けるのですが、より詳細は【NEAT】python3(anaconda3)を使ってNEATを実装してみた(1/5)で説明します。
最後のsimple initial populationは”初期状態として単純なANNを用いる”として「ANNを使ってNEATを考える」で触れました。ここでは、populationはANNのことを指します。単純なpopulationとは種に分かれておらず、多様性がないpopulationのことを指します。TWEEANsは初期状態としてランダムなpopulationを用意したので、初めから多様性がありました。一方、NEATは最初は多様性はありませんが、世代を経るに従って多様性が生まれます。NEATでこのようにしたことにはメリットがあります。それは必要以上の計算コストを抑えることです。Stanleyが調べた結果、TWEEANsは必要以上の計算をしており、それは意味のないことだったそうです。なるべく少ないコストでコンピュータ計算をしたいということから初期状態のpopulationは小さい構造のANNを使用することにしました。
####■NEATのその後
NEATは約20年前に登場し、その後については様々な変化を遂げています(rtNEAT, hyperNEATなど)。
hyperNEATはその名の通りさらにハイパーとなりました。
これもNEATを基にパフォーマンスを向上させた結果として机(?)が歩いています!笑
NEATの時よりもさらに細かなANNを用いて行っているそうです。
最後まで読んでくださり、ありがとうございました!!
##参考文献
Kenneth O. Stanleyが2017年にNEATについて説明しています
・Neuroevolution: A different kind of deep learning
GAの第一人者John H Hollandが86才で亡くなりました
・John Henry Holland, Who Computerized Evolution, Dies at 86
2019年のレビュー
・Evolutionary Algorithms: A Critical Review and its
Future Prospects
1997年の論文、1900年代のGAについて細かく書かれています
・A history of evolutionary computation
John H Hollandによる1962年の論文、適応システムを研究するに際してどのような要素が必要かが書いてあります
・Outline for a Logical Theory of Adaptive Systems