本記事では、教師なし学習と脳科学、そして教師なし学習でMNISTで高性能を出すIICの実装を解説します。
本記事で着目する論文は、
Invariant Information Clustering for Unsupervised Image Classification and Segmentation
です。
この論文では相互情報量と呼ばれる指標を活用し、教師なし学習のクラスタリングで手書き数字画像を分類します。
IIC(Invariant Information Clustering)と呼ばれます。
本記事では、脳科学と教師なし学習、IICのポイン、MNISTでの実装例を解説します。
目次は以下の通りです。
- 脳科学と教師なし学習
- 人工知能界隈での教師なし学習への着目
- 提案手法IICのポイント
- MNISTでIICの実装(Google ColabratoryとPyTorch)
なお、実装コード「MNIST_IIC.ipynb」はこちらに配置しています。
実装コードのリポジトリ
1. 脳科学と教師なし学習
昨今のAI・人工知能のブームはディープラーニング技術にけん引されています。
しかし、ディープラーニングの多くは教師あり学習、もしくは強化学習(アルファ碁など)です。
あまり、教師なし学習にディープラーニングを用いるのは一般的ではありません
(AutoEncoderに代表される次元圧縮は見かけますが、クラスタリングは少ないですね)。
脳科学の分野に目を向けてみると、
OIST(沖縄科学技術大学院大学)の銅谷先生の書籍
「計算神経科学への招待」脳の学習機構の理解を目指して」
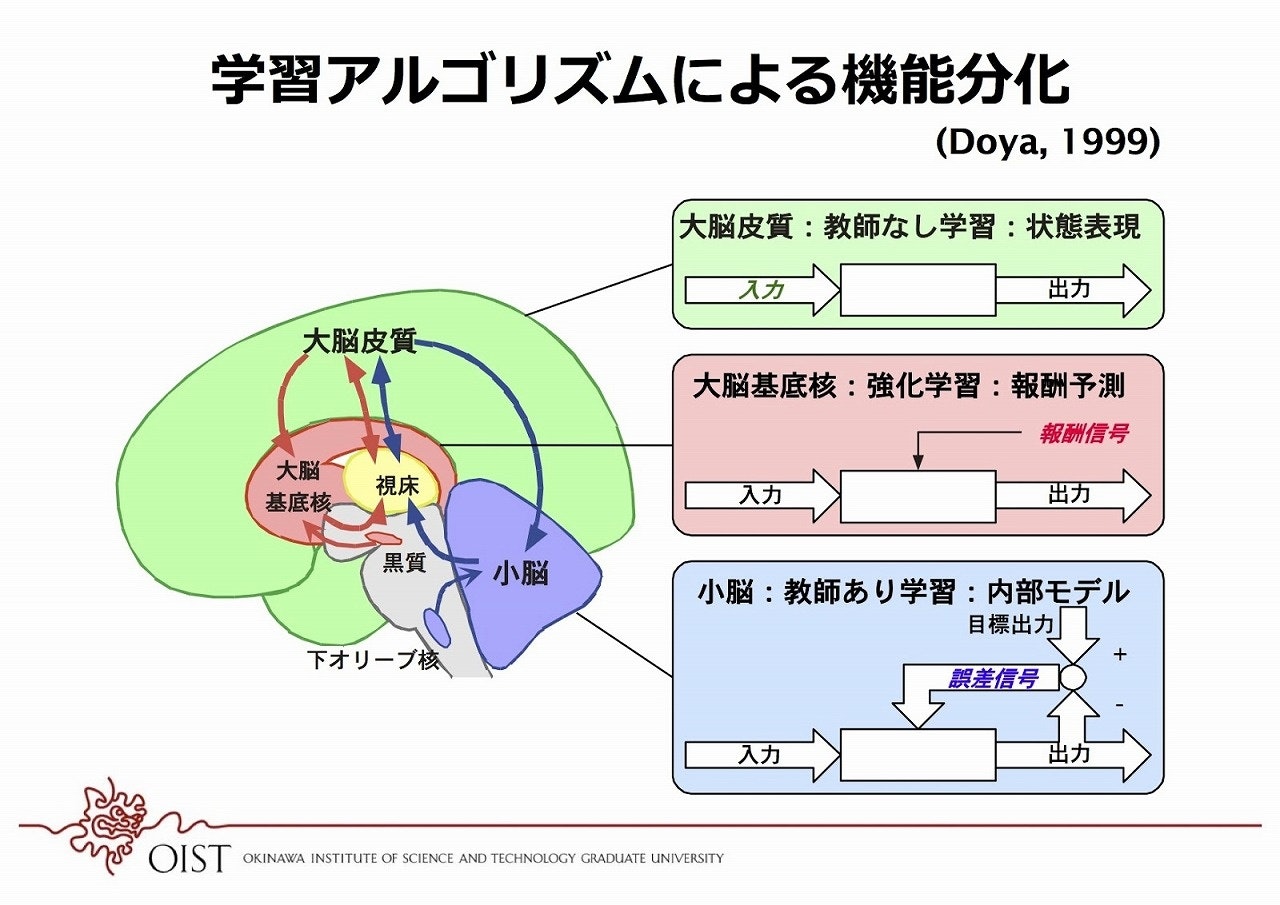
などでは、以下の図ように人工知能の3つの学習タイプと脳との関連が示唆されています。
画像引用:脳の回路モジュールはなぜうまくつながることができるのか--沖縄科技大 銅谷賢治教授
ヒトが他の生物と知能で一線を画すのは、大脳皮質(特に前頭葉)の発達であり、
その大脳皮質では、教師なし学習の重要性が示唆されています。
1981年にノーベル生理学・医学賞を受賞した、ヒューベルとウィーセルの研究は脳科学の研究者の間でも有名です。
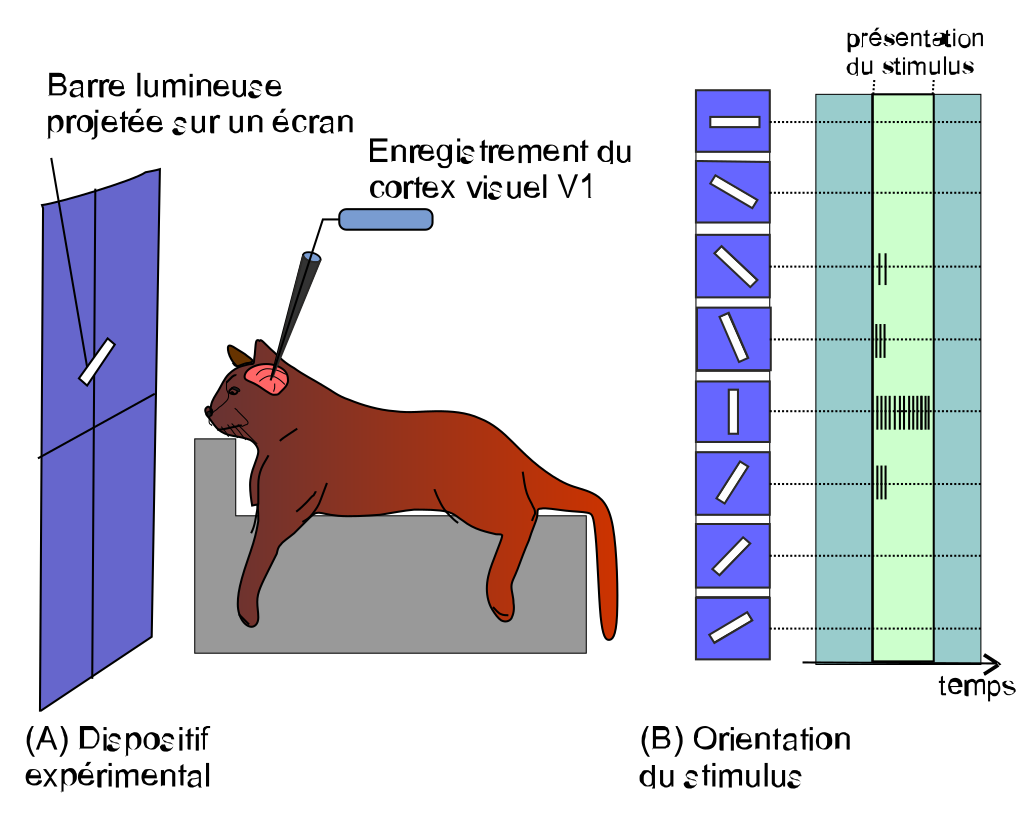
彼らは、ネコの脳の神経細胞に電極を刺し、
様々な記号や動く棒を見せたときの、神経細胞の活動を計測して、
大脳皮質の視覚野では、各神経細胞は記号の提示位置や棒の伸びている方向(縦方向、横方向、斜め方向)など、
提示された物体に応じて神経細胞は選択的に活動することを明らかにしました。
以下の図の場合、この神経細胞は縦棒に強く反応するニューロンです。
つまり、横棒に対応する神経細胞、縦棒に対応する神経細胞などが存在し、それらニューロンの処理が複合的に処理されて物体を認知しているのではという内容です。
その後、21世紀には、
顔画像に対応して発火する脳部位や、特定の有名人に対応して発火する脳部位が発見されました。
顔認識のメカニズム〜日経サイエンス2017年10月号より
そのような前提(大脳皮質には物体に特異的に反応するニューロンの存在)があったので、
ディープラーニング登場初期にGoogleが、
ディープラーニングの途中の層にネコの顔に対応するニューロンが生まれたことの発表
は大ニュースでした。
Using large-scale brain simulations for machine learning and A.I.
これは、ディープラーニングが、実際の生物の脳と同じような特性を獲得したことになりますので。
そしてもうひとつ、脳と、とくに教師なし学習に関しての有名な実験があります。
ブラックモアとクーパーの実験です。彼らは、
子猫を一時的に縦線しか見えない環境で育てると、当分の間、横線を認識できない
ということを明らかにしました。
以下の絵のような環境です。
Cats and Vision: is vision acquired or innate?
つまり、ヒューベルとウィーセルが縦棒や横棒に選択的に反応するニューロンの存在を明らかにし、
ブラックモアとクーパーはそういったニューロンは、子猫の発達時期にそうした風景が目にインプットされて大脳皮質で生まれることを明らかにしました。
子ネコの視覚野の発達なので、教師なし学習であり、物体認識には教師なし学習が重要な役割を果たしているであろう、というのが脳科学から知見です。
2. 人工知能界隈での教師なし学習への着目
AIの研究者界隈でも、これまでの教師あり学習のディープラーニングではなく、教師なし学習への取り組みの重要性に着目する発言が目立ちます。
ヒントンは、2017年のPFN岡野原さんのブログでも取り上げられていますが、
Geoffrey Hinton教授も[link]「脳のシナプスは10^14個あるが,人は10^9秒しか生きられない。サンプル数よりパラメータ数の方がずっと多いことになる。(これらのシナプスの重みを決定するためには)1秒あたり10^5個の制約が必要となり,多くの教師無し学習をしているとの考えに行き着く」と述べています。
と述べています。
実際に研究を進め、SimCLR(A Simple Framework for Contrastive Learning of Visual Representations)を2020年2月に発表しています。
画像引用とSimCLRの解説:SimCLR:対照学習により自己教師学習の性能を向上
SimCLRでは、同じ画像に異なる変換したペアを入力し、それらが同一であることを学習させつつ、異なる画像はそれらとは異であることを教師なし学習で学習させ、画像の特徴量を抽出する手法を最初に獲得させます。
また、ヤン・ルカンは2020年2月のAAAIで、
ルカン氏は、深層学習の次なるイノベーションは教師あり学習ではなく、正解タグのないデータから特徴を抽出する「教師なし学習」や、学習データから正解を自ら作り出す「自己教師あり学習(Self-Supervised Learning)」にあるという。「これらは、生まれたばかりの赤ん坊が世界に対して実行しているタスクと同じだ」とルカン氏は説明する。赤ん坊は「正解」を与えなくても自ら学習できる。
と述べています。
深層学習の「ゴッドファーザー」3人が指摘した、現在のAIに足りない点とは
これ以上、脳科学とAIの話を続けると、本来の実装までたどり着かないので、ここらへんで。
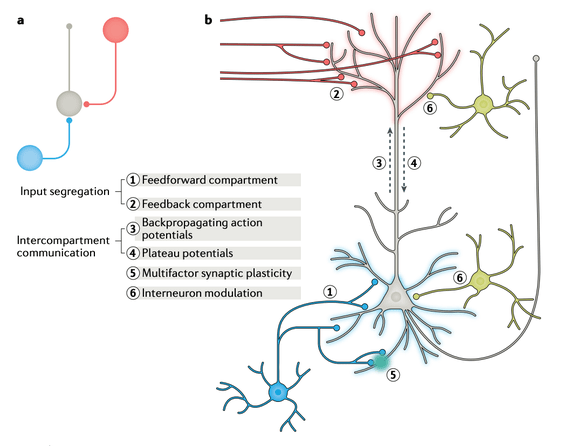
他には、ヒントンが2020年4月のNature Reviews Neuroscienceの論文「Backpropagation and the brain」
Backpropagation and the brain
でのNGRAD則(Neural Gradient Representation by Activity Differences)
を、紹介したりしています。
その他、
●脳科学者とITエンジニアの、DLや汎用人工知能に関する会話
●深層強化学習のビジネス応用と、AIに自然言語を理解させる方法について
も、脳科学とAIについて、おすすめの過去記事です。
3. 提案手法IICのポイント
それでは、今回の論文、
Invariant Information Clustering for Unsupervised Image Classification and Segmentation
での、IIC(Invariant Information Clustering)のポイントを解説します。
なお、IIC論文そのものには「脳の働きがどう・・・」みたいな記述はなく、純粋な計算手法の論文です。
IICのポイントは2つです。
1点目は入力です。
入力には
・データ(今回は手書き数字画像)
・データを適当に変換したもの
の、2つを使用します。
ネットワークにはそれぞれを入力して、それぞれの出力を得ます。
IICのディープラーニングのネットワークは教師あり学習と同じような形です。
出力層のニューロン数は10個(数字の0から9に対応)です。
出力にsoftmax関数をかけ算して、入力画像が0から9の、いずれかである確率値を出力させます。
ポイントの2点目は損失関数です。
教師なし学習なので、教師ラベルは使用しません。
その代わりに、
・ニューラルネットワークに手書き数字画像を入力して出てくる出力ベクトル(要素数は10個)
と、
・手書き数字画像をランダムに少し変換した画像を入力して出てくる出力ベクトル(要素数は10個)
の相互情報量を計算して、それが最大となるように学習させます。
そのため、IICを理解するには相互情報量とお友達になる必要があります。
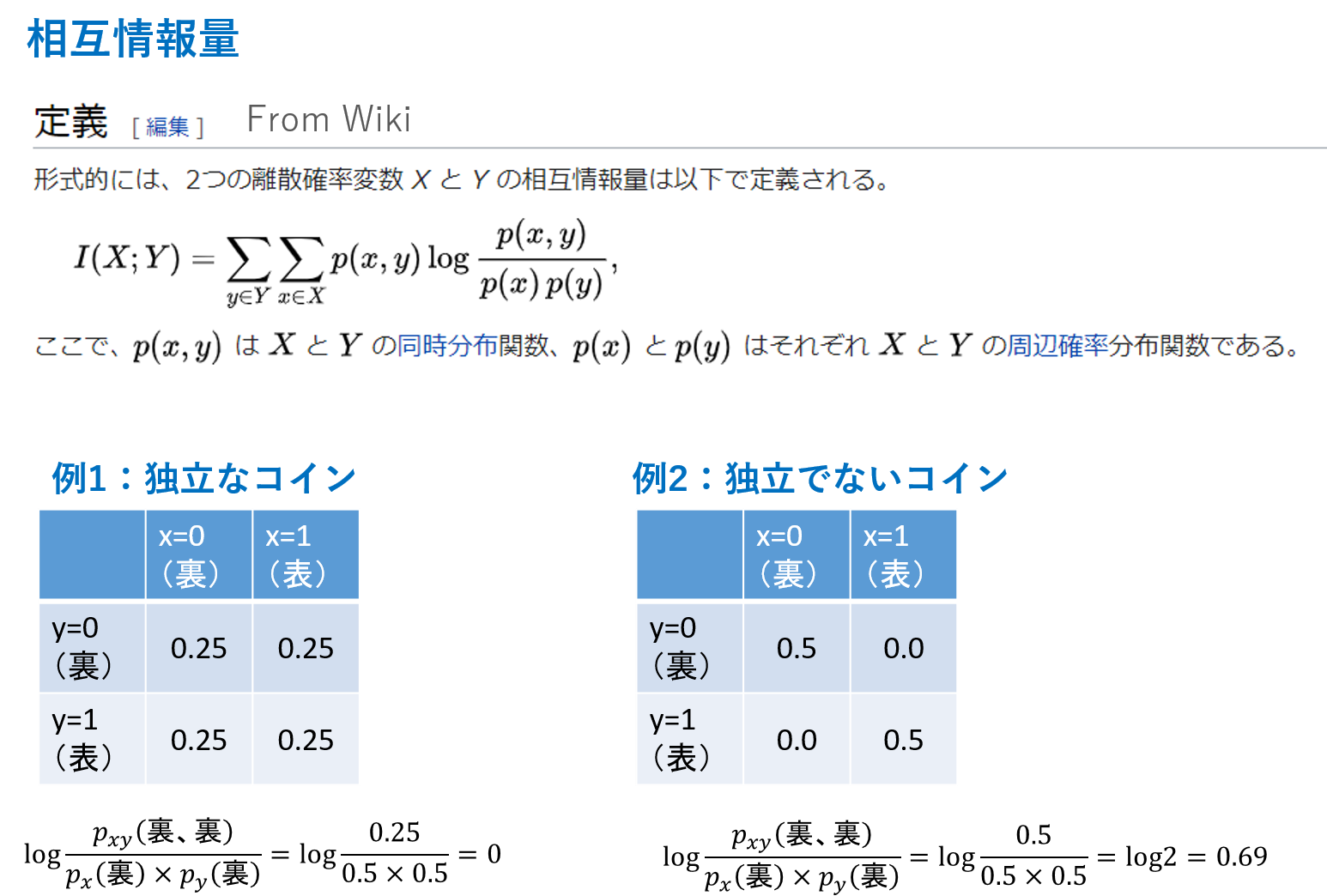
以下に相互情報量を解説したスライドを示します。
なにやら難しい式が並んでいますが、結局、2つのデータが共有してもつ情報のことを相互情報量と呼びます。
logの中の同時分布と周辺確率分布がカギです。
上の絵では、例1に独立な2枚のコインを投げた場合、例2に独立でないコインを2枚投げた例を示しています。
(つまり、例2は2枚目のコインは1枚目と同じ結果になる)
上の絵はコインの例で、裏か表の2つを出力します。
MNISTのニューラルネットワークの場合は、0から9の10個を出力します。
MNISTのニューラルネットワークの出力2つ版が、上記のコイン投げだと思ってください。
例1の2つが独立の場合、(裏、裏)となる確率は0.25です。
そして、周辺化をして、1枚目が裏になる確率は、(裏、裏)+(裏、表)で0.5です。
同様に2枚目が裏になる確率も(表、裏)+(裏、裏)で0.5です。
これらをlogの計算に入れると、logの結果が0になります。
(裏、裏)だけでなく、(裏、表)、(表、裏)、(表、表)を計算すると、全部0で、その総和は0になります。
よって、独立なコインを2枚投げた場合、1回目の結果と2回目の結果の相互情報量は0です。
コイン投げの試行は独立であり、1回目の結果と2回目の結果は無関係なので、互いに持ちあう情報は存在せず、0になるのも納得いただけるかと思います。
例2の独立でない、2枚目のコインは1枚目と同じ結果になる場合の相互情報量を考えてみます。
(裏、裏)となる確率は0.5です。
そして周辺化をして、1枚目が裏になる確率は(裏、裏)+(裏、表)で0.5です。
同様に2枚目も0.5です。
すると、logのなかの計算は(1/0.5)となり、log2 = 0.69となります。
ここに、(裏、裏)の確率0.5がかけ算されて、約0.35となります。
(裏、表)は0、(表、表)は(裏、裏)と同様に約0.35、(表、裏)は0なので、総和は0.69となります。
よって、独立でないコイン投げの場合は相互情報量が0より大きな値になります。
つまり、1枚目にコイン投げの結果と2枚目のコイン投げの結果が情報を持ちあっていることになります。
今回は2枚目の結果が1枚目と同じにしているので、納得いただけるかと思います。
IICではこれがMNIST画像の出力0-9の10種類バージョンのコイン投げと思ってください。
そして、2枚目のコインというのは、MNIST画像に適当な変換をかけたものです。
適当な変換としては、アフィン変換で画像を回転引き伸ばしし、さらにノイズがのっかります。
この多少の変換を受けた画像も、元の画像も、数字の0から9のいずれかである確率の出力結果がが同じになるようにネットワークを学習させたい
というのがIICの気持ちになります。
多少の変換を受けた画像というのは、結局、同じクラスの画像を模擬していることになります。
ここでポイントが2つあります。
まず、ネットワークの出力は数字の0から9に順番に対応しているわけではなく、また数字に対応しているわけでもありません。
ただ単に、似た画像は同じクラスになるように分けるだけです。
2点目が、「それでは全部、同じクラスならないか?」という心配ですが、コイン投げの相互情報量を思い出してください。
例2の2枚目のコインは1枚目と同じ結果になる場合です。
全部裏が出るコインより、表・裏が同じくらいに出るコインの方が相互情報量は大きくなります。
全部が裏が出るコインでは(裏、裏)となる確率は1.0です。
そして周辺化をして、1枚目が裏になる確率は(裏、裏)+(裏、表)で1.0です。
同様に2枚目も1.0です。
すると、logのなかの計算は(1/1)となり、log1 = 0.0となります。
相互情報量を最大化するためには、とれる種類が2種類なら2種類満遍なく、そして10種類であれば10種類満遍なく確率が分散する方が相互情報量は最大化されます。
そのため、ミニバッチ分を計算していれば、自然とバラバラの10クラスが満遍なく存在するようになります。
以上が、IICのポイント解説です。
続いて実装に入ります。
4. MNISTでIICの実装(Google ColabratoryとPyTorch)
環境はGoogle Colaboratory、フレームワークはPyTorchを使用します。
MNISTに対して、IICを実装します。
なお、実装コード「MNIST_IIC.ipynb」はこちらに配置しています。
実装コードのリポジトリ
https://github.com/RuABraun/phone-clustering
を参考に実装しますが、だいぶ変更を加えています。
最初に、シードを固定します
# 乱数のシードを固定
import os
import random
import numpy as np
import torch
SEED_VALUE = 1234 # これはなんでも良い
os.environ['PYTHONHASHSEED'] = str(SEED_VALUE)
random.seed(SEED_VALUE)
np.random.seed(SEED_VALUE)
torch.manual_seed(SEED_VALUE) # PyTorchを使う場合
続いて、GPU使用を確認します。
Google Colaboratoryの場合は、上部メニューの「ランタイム」から
「ランタイムのタイプを変更」を選択し、NoneをGPUに切り替えておきます。
# GPUが使えるときにはGPUに(Google Colaboratoryの場合はランタイムからGPUを指定)
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(device)
# GPUを使用。cudaと出力されるのを確認する。
MNISTの画像をダウンロードして、PyTorchのデータローダーにします。
訓練とテストを用意します。
# MNISTの画像をダウンロードし、DataLoaderにする(TrainとTest)
from torchvision import datasets, transforms
batch_size_train = 512
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('.', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
])),
batch_size=batch_size_train, shuffle=True, drop_last=True)
# drop_lastは最後のミニバッチが規定のサイズより小さい場合は使用しない設定
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('.', train=False, transform=transforms.Compose([
transforms.ToTensor(),
])),
batch_size=1024, shuffle=False)
続いて、IICのディープラーニングモデルです。
通常の教師あり学習と同じなのですが、ネットワークでより豊かな表現力を獲得するため、ただの教師あり学習のときよりは重たい構成にしています。
そして最終出力層は0-9に対応すると期待したい10種類のクラスのものと、別途、overclustringと呼ばれる技術も使用します。
これは期待する10種類よりもさらに多くに分類させます。
最終出力層は10種類版とoverclustering版になり、損失関数もその両方のアウトプットを計算して総和を使用します。
overclustringするネットワークで微細な変化を捉えられるようになれば、通常の10種類のクラス分類の性能もアップするだとうという期待です。
またIIC論文ではmulti-headとして、この出力層をさらに多重化しています。
これは出力層の初期値依存での失敗などを防ぐためとされていますが、
私の感覚的にはあまり意味がなく、実装も面倒になるので、省略しました。
# ディープラーニングモデル
import torch.nn as nn
import torch.nn.functional as F
OVER_CLUSTRING_Rate = 10 # 多めに分類するoverclsuteringも用意する
class NetIIC(nn.Module):
def __init__(self):
super(NetIIC, self).__init__()
self.conv1 = nn.Conv2d(1, 128, 5, 2, bias=False)
self.bn1 = nn.BatchNorm2d(128)
self.conv2 = nn.Conv2d(128, 128, 5, 1, bias=False)
self.bn2 = nn.BatchNorm2d(128)
self.conv3 = nn.Conv2d(128, 128, 5, 1, bias=False)
self.bn3 = nn.BatchNorm2d(128)
self.conv4 = nn.Conv2d(128, 256, 4, 1, bias=False)
self.bn4 = nn.BatchNorm2d(256)
# 0-9に対応すると期待したい10種類のクラス
self.fc = nn.Linear(256, 10)
# overclustering
# 実際の想定よりも多めにクラスタリングさせることで、ネットワークで微細な変化を捉えられるようにする
self.fc_overclustering = nn.Linear(256, 10*OVER_CLUSTRING_Rate)
def forward(self, x):
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
x = F.relu(self.bn4(self.conv4(x)))
x_prefinal = x.view(x.size(0), -1)
y = F.softmax(self.fc(x_prefinal), dim=1)
y_overclustering = F.softmax(self.fc_overclustering(
x_prefinal), dim=1) # overclustering
return y, y_overclustering
モデルの重みの初期化関数を定義しておきます。
import torch.nn.init as init
def weight_init(m):
"""重み初期化"""
if isinstance(m, nn.Conv2d):
init.xavier_normal_(m.weight.data)
if m.bias is not None:
init.normal_(m.bias.data)
elif isinstance(m, nn.BatchNorm2d):
init.normal_(m.weight.data, mean=1, std=0.02)
init.constant_(m.bias.data, 0)
elif isinstance(m, nn.Linear):
# Xavier
#init.xavier_normal_(m.weight.data)
# He
init.kaiming_normal_(m.weight.data)
if m.bias is not None:
init.normal_(m.bias.data)
続いて、入力画像とペアになる画像を作るための変換を定義します。
アフィン変換で回転引き伸ばしをして、その後各ピクセルにノイズを加えます。
# データにノイズを加える関数の定義
import torchvision as tv
import torchvision.transforms.functional as TF
def perturb_imagedata(x):
y = x.clone()
batch_size = x.size(0)
# ランダムなアフィン変換を実施
trans = tv.transforms.RandomAffine(15, (0.2, 0.2,), (0.2, 0.75,))
for i in range(batch_size):
y[i, 0] = TF.to_tensor(trans(TF.to_pil_image(y[i, 0])))
# ノイズを加える
noise = torch.randn(batch_size, 1, x.size(2), x.size(3))
div = torch.randint(20, 30, (batch_size,),
dtype=torch.float32).view(batch_size, 1, 1, 1)
y += noise / div
return y
そして、IICのキモである、相互情報量の計算です。
実施している内容は、3. で説明した通りの相互情報量の計算です。
相互情報量を最大化したいのですが、損失にするために、マイナスをかけ算して、
最小化問題に置き換えています。
また、
教師なし学習でMNISTの正解率を97%以上出す簡単な手法(転移学習なし)
で紹介されていた相互情報量の計算に係数項を加え、よりクラスがバラつきやすいようにしています。
上記の記事はTensorFlow2での実装が丁寧に紹介されており、TensorFlowの方にとてもおすすめです。
# IISによる損失関数の定義
# 参考:https://github.com/RuABraun/phone-clustering/blob/master/mnist_basic.py
import sys
def compute_joint(x_out, x_tf_out):
# x_out、x_tf_outは torch.Size([512, 10])。この二つをかけ算して同時分布を求める、torch.Size([2048, 10, 10])にする。
# torch.Size([512, 10, 1]) * torch.Size([512, 1, 10])
p_i_j = x_out.unsqueeze(2) * x_tf_out.unsqueeze(1)
# p_i_j は torch.Size([512, 10, 10])
# 全ミニバッチを足し算する ⇒ torch.Size([10, 10])
p_i_j = p_i_j.sum(dim=0)
# 転置行列と足し算して割り算(対称化) ⇒ torch.Size([10, 10])
p_i_j = (p_i_j + p_i_j.t()) / 2.
# 規格化 ⇒ torch.Size([10, 10])
p_i_j = p_i_j / p_i_j.sum()
return p_i_j
# 結局、p_i_jは通常画像の判定出力10種類と、変換画像の判定10種類の100パターンに対して、全ミニバッチが100パターンのどれだったのかの確率分布表を示す
def IID_loss(x_out, x_tf_out, EPS=sys.float_info.epsilon):
# torch.Size([512, 10])、後ろの10は分類数なので、overclusteringのときは100
bs, k = x_out.size()
p_i_j = compute_joint(x_out, x_tf_out) # torch.Size([10, 10])
# 同時確率の分布表から、変換画像の10パターンをsumをして周辺化し、元画像だけの周辺確率の分布表を作る
p_i = p_i_j.sum(dim=1).view(k, 1).expand(k, k)
# 同時確率の分布表から、元画像の10パターンをsumをして周辺化し、変換画像だけの周辺確率の分布表を作る
p_j = p_i_j.sum(dim=0).view(1, k).expand(k, k)
# 0に近い値をlogに入れると発散するので、避ける
#p_i_j[(p_i_j < EPS).data] = EPS
#p_j[(p_j < EPS).data] = EPS
#p_i[(p_i < EPS).data] = EPS
# 参考GitHubの実装(↑)は、PyTorchのバージョン1.3以上だとエラーになる
# https://discuss.pytorch.org/t/pytorch-1-3-showing-an-error-perhaps-for-loss-computed-from-paired-outputs/68790/3
# 0に近い値をlogに入れると発散するので、避ける
p_i_j = torch.where(p_i_j < EPS, torch.tensor(
[EPS], device=p_i_j.device), p_i_j)
p_j = torch.where(p_j < EPS, torch.tensor([EPS], device=p_j.device), p_j)
p_i = torch.where(p_i < EPS, torch.tensor([EPS], device=p_i.device), p_i)
# 元画像、変換画像の同時確率と周辺確率から、相互情報量を計算
# ただし、マイナスをかけて最小化問題にする
"""
相互情報量を最大化したい
⇒結局、x_out, x_tf_outが持ちあう情報量が多くなって欲しい
⇒要は、x_out, x_tf_outが一緒になって欲しい
p_i_jはx_out, x_tf_outの同時確率分布で、ミニバッチが極力、10×10のいろんなパターン、満遍なく一様が嬉しい
前半の項、torch.log(p_i_j)はp_ijがどれも1に近いと大きな値(0に近い)になる。
どれかが1であと0でバラついていないと、log0で小さな値(負の大きな値)になる
つまり前半の項は、
後半の項は、元画像、もしくは変換画像について、それぞれ周辺化して10通りのどれになるかを計算した項。
周辺化した10×10のパターンを引き算して、前半の項が小さくなるのであれば、
x_outとx_tf_outはあまり情報を共有していなかったことになる。
"""
# https://qiita.com/Amanokawa/items/0aa24bc396dd88fb7d2a
# を参考に、重みalphaを追加
# 同時確率分布表のばらつきによる罰則を小さく = 同時確率の分布がバラつきやすくする
alpha = 2.0 # 論文や通常の相互情報量の計算はalphaは1です
loss = -1*(p_i_j * (torch.log(p_i_j) - alpha *
torch.log(p_j) - alpha*torch.log(p_i))).sum()
return loss
訓練を実施します。
# 訓練の実施
total_epoch = 20
# モデル
model = NetIIC()
model.apply(weight_init)
model.to(device)
# 最適化関数を設定
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
def train(total_epoch, model, train_loader, optimizer, device):
model.train()
scheduler = torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(
optimizer, T_0=2, T_mult=2)
for epoch in range(total_epoch):
for batch_idx, (data, target) in enumerate(train_loader):
# 学習率変化
scheduler.step()
# 微妙に変換したデータを作る。SIMULTANEOUS_NUM分のペアを作る
data_perturb = perturb_imagedata(data) # ノイズを与える
# GPUに送れる場合は送る
data = data.to(device)
data_perturb = data_perturb.to(device)
# 最適化関数の初期化
optimizer.zero_grad()
# ニューラルネットワーク出力
output, output_overclustering = model(data)
output_perturb, output_perturb_overclustering = model(data_perturb)
# 損失の計算
loss1 = IID_loss(output, output_perturb)
loss2 = IID_loss(output_overclustering,
output_perturb_overclustering)
loss = loss1 + loss2
# 損失を減らすように更新
loss.backward()
optimizer.step()
# ログ出力
if batch_idx % 10 == 0:
print('Train Epoch {}:iter{} - \tLoss1: {:.6f}- \tLoss2: {:.6f}- \tLoss_total: {:.6f}'.format(
epoch, batch_idx, loss1.item(), loss2.item(), loss1.item()+loss2.item()))
return model, optimizer
model_trained, optimizer = train(
total_epoch, model, train_loader, optimizer, device)
訓練時には、schedulerのCosineAnnealingWarmRestartsを使用して、学習率を変化させています。
このschedulerは以下に示すような学習率の上下をします。

図:引用
https://www.kaggle.com/c/imet-2019-fgvc6/discussion/94783
学習率が低下して急激に大きくなるときに、局所解から抜け出すことができ、大域的な極小解のパラメータへと近づきやすくなります。
最後に、訓練されたモデルでテストデータを推論します。
# モデル分類のクラスターの結果を確認する
def test(model, device, train_loader):
model.eval()
# 結果を格納するリスト
out_targs = []
ref_targs = []
cnt = 0
with torch.no_grad():
for data, target in test_loader:
cnt += 1
data = data.to(device)
target = target.to(device)
outputs, outputs_overclustering = model(data)
# 分類結果をリストに追加
out_targs.append(outputs.argmax(dim=1).cpu())
ref_targs.append(target.cpu())
# リストをひとまとめに
out_targs = torch.cat(out_targs)
ref_targs = torch.cat(ref_targs)
return out_targs.numpy(), ref_targs.numpy()
out_targs, ref_targs = test(model_trained, device, train_loader)
最後に出力結果の頻度表を求めます。
縦軸が実際の0から9のラベルを、横軸が判定されたクラスを示します。
import numpy as np
import scipy.stats as stats
# 混同行列(的な)を作る
matrix = np.zeros((10, 10))
# 縦に数字の0から9を、横に判定されたクラスの頻度表を作成
for i in range(len(out_targs)):
row = ref_targs[i]
col = out_targs[i]
matrix[row][col] += 1
np.set_printoptions(suppress=True)
print(matrix)
出力結果は、
[[ 1. 978. 1. 0. 0. 0. 0. 0. 0. 0.]
[ 1. 0. 4. 1110. 2. 0. 2. 0. 13. 3.]
[ 0. 5. 4. 0. 0. 0. 0. 0. 1023. 0.]
[ 0. 0. 2. 0. 0. 4. 962. 0. 39. 3.]
[ 1. 0. 0. 0. 960. 0. 0. 19. 1. 1.]
[ 1. 1. 0. 0. 0. 866. 17. 0. 3. 4.]
[ 940. 7. 0. 0. 0. 3. 0. 0. 4. 4.]
[ 0. 0. 921. 1. 0. 0. 1. 92. 13. 0.]
[ 0. 6. 0. 0. 0. 2. 4. 2. 2. 958.]
[ 0. 4. 14. 0. 2. 7. 27. 949. 2. 4.]]
となり、例えば数字の0はクラスの1番目に978個集まっています。
数字の9であれば、7番目に949個集まっています。
各推定されたクラスで同じ数字が固まっているのを、各正解ラベルと当てはめると、
# 全データ
total_num = matrix.sum().sum()
print(total_num)
# 各数字がきれいに各クラスに分かれている。
# 例えば数字の0はクラスの1番目に978個集まった。数字の9であれば、7番目に949個集まった。
# よって、最大のものを足していくと、正解の個数なので
correct_num_list = matrix.max(axis=0)
print(correct_num_list)
print(correct_num_list.sum())
print("正解率:", correct_num_list.sum()/total_num*100)
で、出力は
10000.0
[ 940. 978. 921. 1110. 960. 866. 962. 949. 1023. 958.]
9667.0
正解率: 96.67
です。正解率は97%となりました。
なお、実装コード「MNIST_IIC.ipynb」はこちらに配置しています。
実装コードのリポジトリ
さいごに
相互情報量の最大化を利用した教師なし学習である、IIC(Invariant Information Clustering)を紹介しました。
IICの同じ画像からよく似た入力を同一とみなさせる思想は、ヒントンらの最新論文のSimCLR(A Simple Framework for Contrastive Learning of Visual Representations)の対照学習ともよく似ています。
IIC自体は相互情報量が誤差関数に出てくるだけで、IIC論文と生物の脳ですと、なかなかに隔たりは大きいです。
ですが、相互情報量はカルバック・ライブラー情報量でも表すことができ、カール・フリストンの自由エネルギー原理(free-energy principle)まで展開できる(気がします)。
IICはなかなかに面白い論文と手法でした。
今後、こうした教師なし学習の進歩と脳・神経科学の進歩がもっと融合していけばと思います。
今回は画像データでIICを実施しましたが、ではBERTで処理したテキストデータでIICをするとどうなるのかについて、次回は記事を書こうと思います(ここに、物体認識という視覚野を持つ生物に普遍的の脳の仕組みと、自然言語というヒト特有の性質の差が顕著にでてきて面白い結果です)。
以上、ご一読いただき、ありがとうございました。
【免責】本記事は著者の意見/発信であり、著者が属する企業等の公式見解ではございません