就職活動ネタとして記事を初投稿。
精度が高いと言われている教師無し学習、IIC(Invariant Information Clustering)の論文を読み解き実装してみました。
IICとは、相互情報量を最大化することでクラスタリングを行う手法のことです。
IICの論文はこちら
Invariant Information Clustering for Unsupervised Image Classification and Segmentation
Xu Ji, João F. Henriques, Andrea Vedaldi
使ったフレームワークはTensorFlow2.0。対象データはお馴染みのMNIST。
相互情報量について
相互情報量の解釈は複数ありますが、今回の機械学習を説明しやすいシンプルな方法を選びます。
確率分布Xに対する情報エントロピーH(X)は以下で定義される。
H(X) = -\sum_{i}x_{i} \ln x_{i}
この量は分布が一様分布に近いほど値が大きくなり、分布が一点に収束した時0となります。
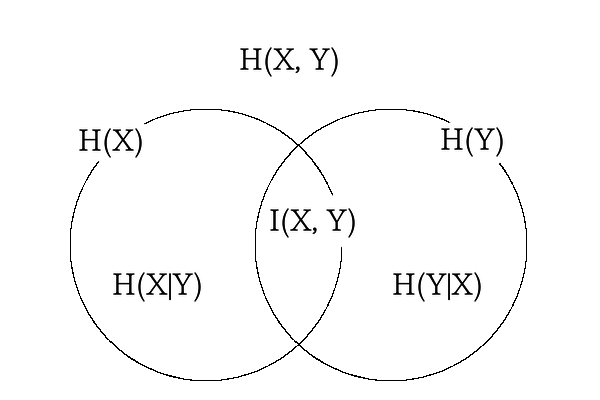
相互情報量$I$は、二つの独立でない確率分布$X$, $Y$の情報エントロピーの集合が一致している量といえる。
I(X, Y) = H(X) + H(Y) - H(X,Y)
図からわかるように相互情報量$I$を最大化する事は、$X$と$Y$の情報エントロピーを近づけ、かつ$X$と$Y$の情報エントロピーを大きくすることになります。
情報エントロピーを近づけることでネットワークの表現学習が進み、情報エントロピーを大きくすることでクラスタリングが一点に集中すること(縮退)を防ぐ効果がある。
実際の学習では、画像ペア($X$, $X'$)に対するネットワークからのsoftmax出力を($Z$, $Z'$)としたとき、$Z$, $Z'$の同時確率を対称化させた行列$P$の周辺確率$P_{x}, P_{y}$について相互情報量を最大化させます。
損失関数の具体的な式を求めると以下となる。
\begin{align}
I(P_{x}, P_{y}) &= -\sum_{i}P_{x(i)} \ln P_{x(i)}-\sum_{j}P_{y(j)} \ln P_{y(j)}+\sum_{i}\sum_{j}P_{(i, j)} \ln P_{(i, j)}\\
&=\sum_{i}\sum_{j}\bigl(P_{(i, j)}(-\ln P_{x(i)}-\ln P_{y(j)}+\ln P_{(i, j)})\bigr)\\
&=\sum_{i}\sum_{j}P_{(i, j)}・\ln \frac{P_{(i, j)}}{P_{x(i)} P_{y(j)}}
\end{align}
ペアの画像を作る
学習には画像$X$に対して$X'$のペアを作る必要がある。
$X$, $X'$は同じオブジェクトを含んだデータのペアであるが、インスタンス固有の詳細は異なることが望ましい。
同じオブジェクトのペアなので、ネットワークの出力$Z,Z'$は従属性が高く独立ではなくなるのがポイントだ。
一般には$X$にスケーリング、スキューイング(歪ませる)、回転、反転、コントラストや彩度の変更などの操作を加えて$X'$とする。
今回は以下の4操作を施した。
| 元画像 | 回転 | 歪み | 二値化 | ノイズ |
 |
 |
 |
 |
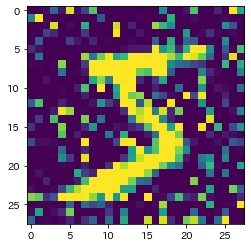 |
ネットワークの構造
転移学習をしたほうが良いのは言うまでもありませんが、今回は単純なタスクなのでシンプルにConvとBNの見慣れた形を作ってみました。
入力28×28×1の画像に対してソフトマックス予測ベクトルを出力します。
出力$Z$はMNISTのクラスタリングであり、ラベルの数と同じ10次元。
他方は論文の中でOverclusteringと呼ばれる手法に使われる出力であり、ラベルの5倍の50次元とした。
Overclusteringは、想定しているクラスタリングの数よりも多いクラスタリングを同時に行うことで、ネットワークがより特徴量を獲得する仕組みである。
この二つの学習について畳み込み層の重みは共有するが、全結合層は別の重みを使用しています。
def create_model(self):
inputs = layers.Input((28,28,1))
x = layers.Conv2D(32, 3, padding="same")(inputs)
x = layers.BatchNormalization()(x)
x = layers.Activation("relu")(x)
x = layers.MaxPooling2D(2)(x)
x = layers.Conv2D(64, 3, padding="same")(x)
x = layers.BatchNormalization()(x)
x = layers.Activation("relu")(x)
x = layers.MaxPooling2D(2)(x)
x = layers.Conv2D(128, 3, padding="same")(x)
x = layers.BatchNormalization()(x)
x = layers.Activation("relu")(x)
x = layers.MaxPooling2D(2)(x)
x = layers.Conv2D(256, 3, padding="same")(x)
x = layers.BatchNormalization()(x)
x = layers.Activation("relu")(x)
conv_out = layers.GlobalAveragePooling2D()(x)
x = layers.Dense(128, activation="relu")(conv_out)
x = layers.Dense(64, activation="relu")(x)
Z = layers.Dense(10, activation="softmax")(x)
x = layers.Dense(128, activation="relu")(conv_out)
x = layers.Dense(64, activation="relu")(x)
overclustering = layers.Dense(50, activation="softmax")(x)
return Model(inputs, [Z, overclustering])
損失関数の定義
モデルに画像ペアのバッチデータ$X, X'$を与え、$Z, Z'$及びOverclusteringの出力を得て、それぞれの相互情報量計算をIICメソッドで行います。
論文にはPytrchでの実装例が載っており、TenosrFlow2.0に書き換えると以下のコードになる。
相互情報量は最大化を目指しますが、機械学習では最小化を行うので損失関数全体にマイナスを掛けている。
最終的なlossはクラスタリングとOverclusteringの平均となり、この値で勾配計算を行います。
def IIC(self, z, z_, c=10):
z = tf.reshape(z, [-1, c, 1])
z_ = tf.reshape(z_, [-1, 1, c])
P = tf.math.reduce_sum(z * z_, axis=0) # 同時確率
P = (P + tf.transpose(P)) / 2 # 対称化
P = tf.clip_by_value(P, 1e-7, tf.float32.max) # logが発散しないようにバイアス
P = P / tf.math.reduce_sum(P) # 規格化
# 周辺確率
Pi = tf.math.reduce_sum(P, axis=0)
Pi = tf.reshape(Pi, [c, 1])
Pi = tf.tile(Pi, [1,c])
Pj = tf.math.reduce_sum(P, axis=1)
Pj = tf.reshape(Pj, [1, c])
Pj = tf.tile(Pj, [c,1])
loss = tf.math.reduce_sum(P * (tf.math.log(Pi) + tf.math.log(Pj) - tf.math.log(P)))
return loss
@tf.function
def train_on_batch(self, X, X_):
with tf.GradientTape() as tape:
z, overclustering = self.model(X, training=True)
z_, overclustering_ = self.model(X_, training=True)
loss_cluster = self.IIC(z, z_)
loss_overclustering = self.IIC(overclustering, overclustering_, c=50)
loss = (loss_cluster + loss_overclustering) / 2
graidents = tape.gradient(loss, self.model.trainable_weights)
self.optim.apply_gradients(zip(graidents, self.model.trainable_weights))
return loss_cluster, loss_overclustering
学習結果
学習パラメータ
optimizerはAdamのrate0.0001
batch_sizeは1000
各変換操作での画像ペアを使い、epoch100まで学習した結果が以下である。
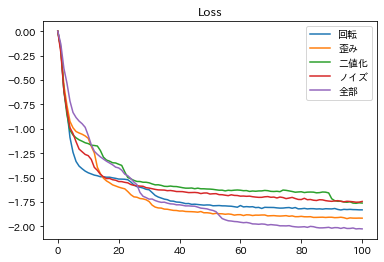
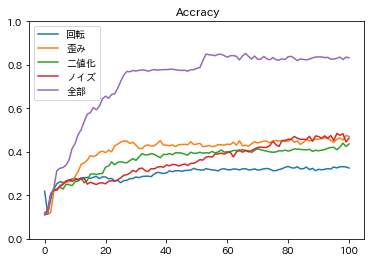
グラフを見ると、変換は単体で行うよりも複数を組み合わせた方が良いとわかる。
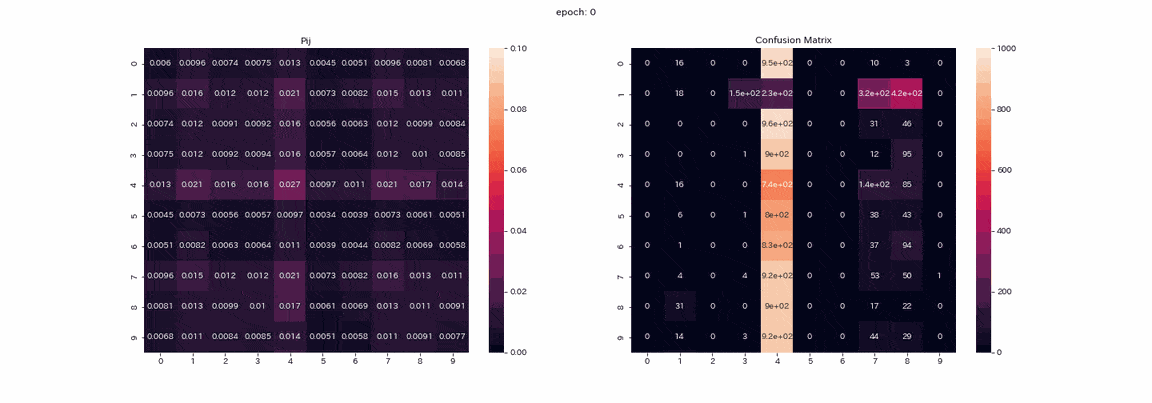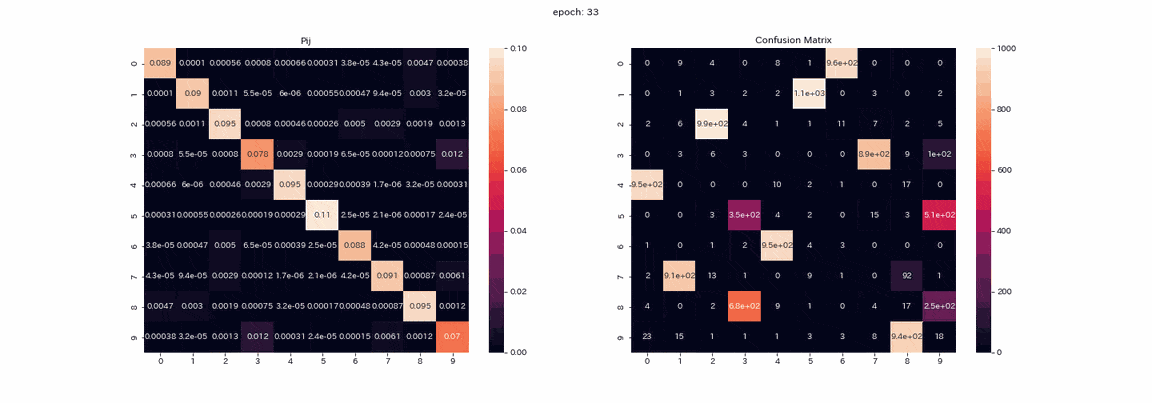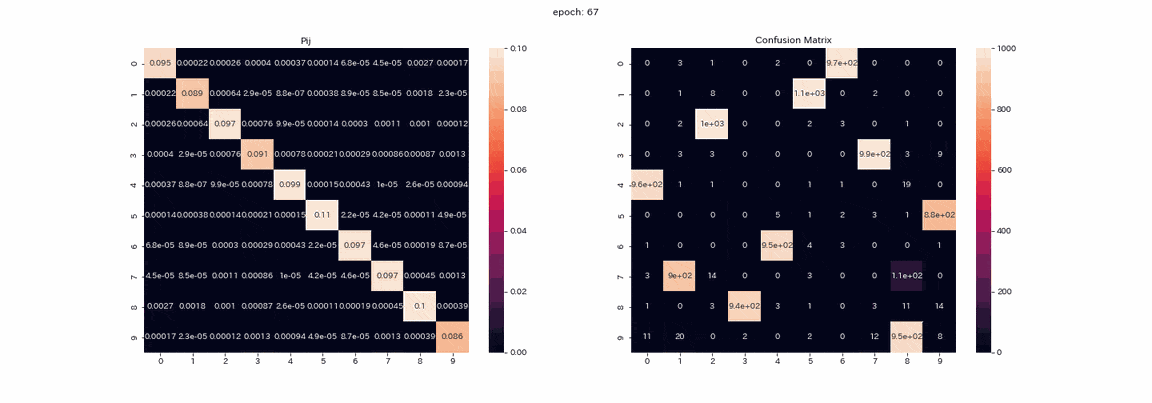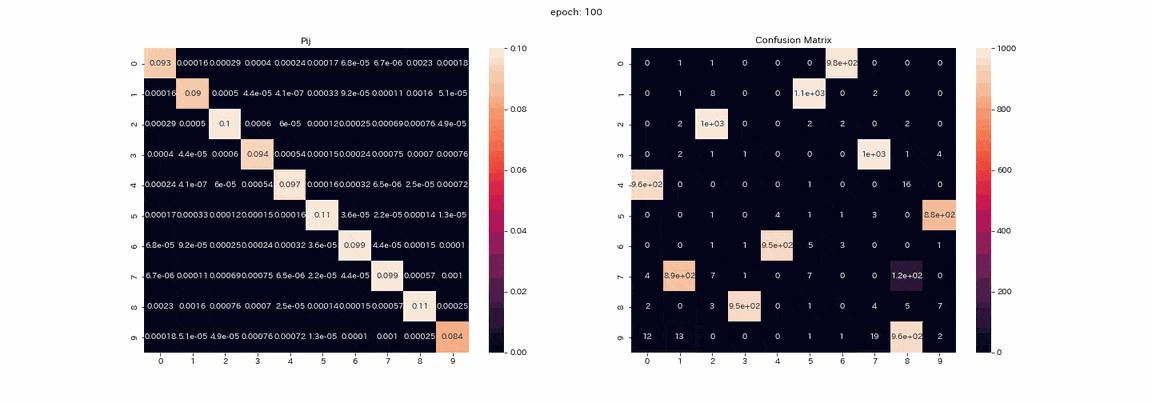
以下は結果が一番良かった4変換すべてを施した画像ペアでの学習で、学習中の行列$P$とテストデータ予測の混合行列(縦軸が真のラベルで、横軸が出力のインデックス)を記録したgifである。
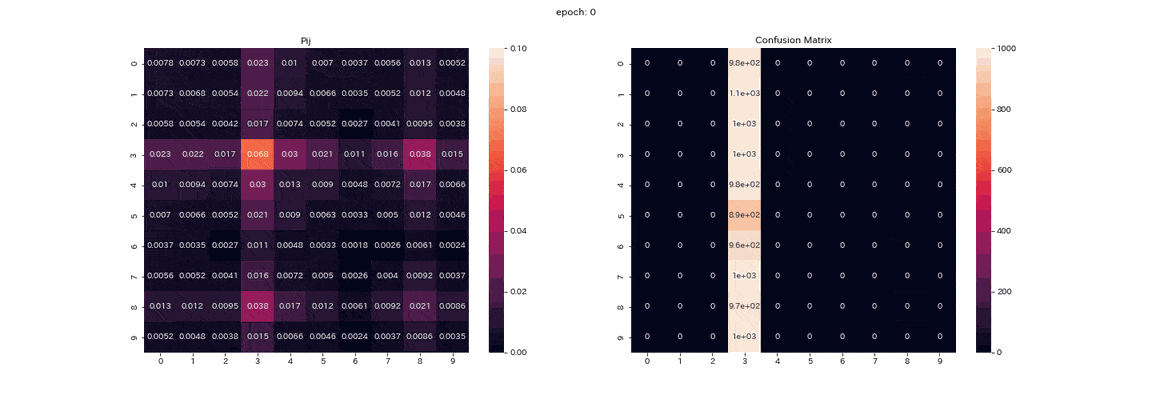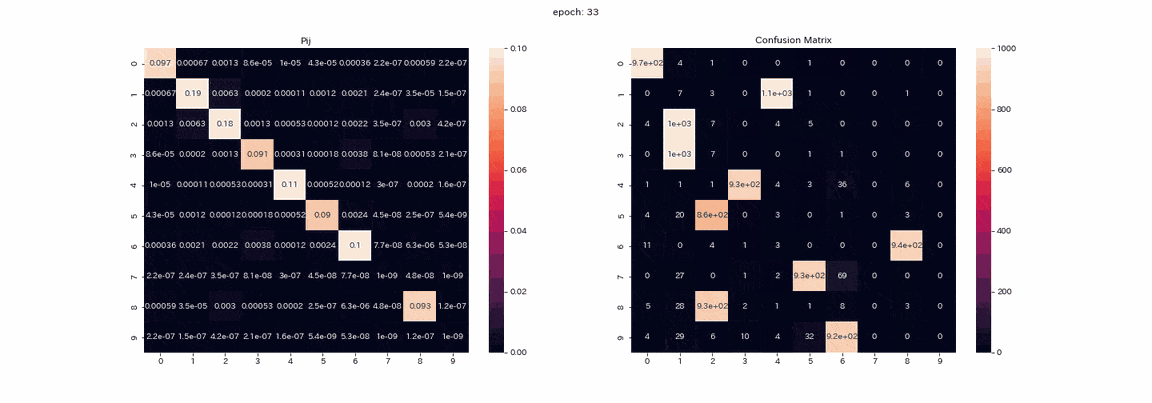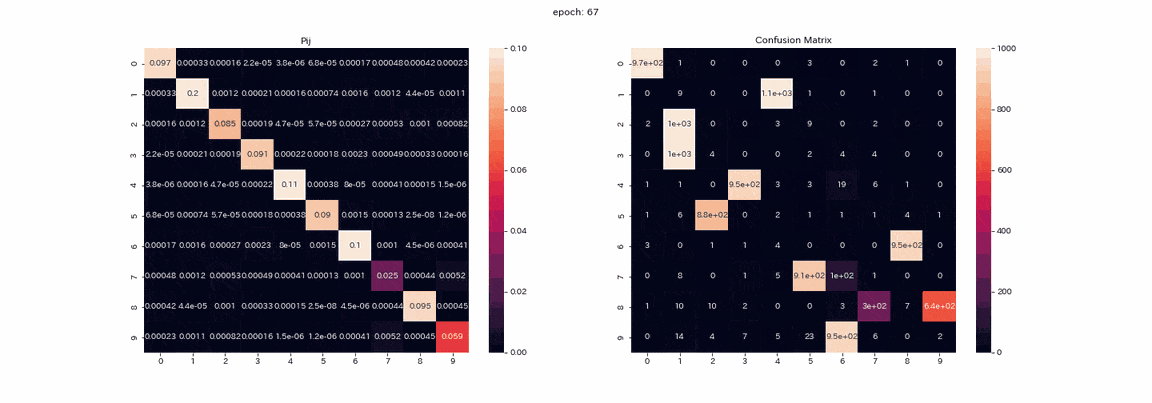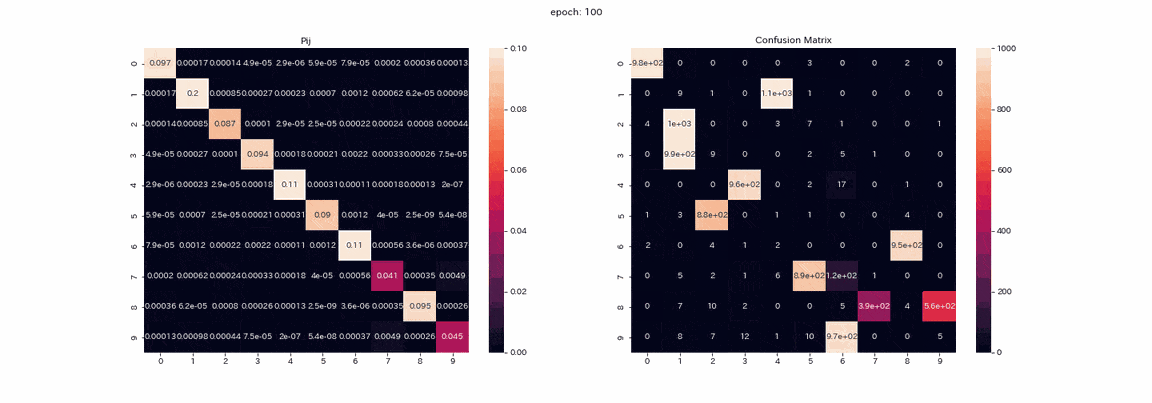
実際は500エポック以上学習しましたが、100エポック以上はあまり変化が見られなかったので学習はほぼ完了したと考えます。
行列$P$では学習が進むにつれて対角に値が並びますが、これは$Z,Z'$が同じ分布を出力するようになるからである。
また、列1の値が他よりも大きいことが確認できます。
混合行列ではラベル2,3の区別ができておらず、ラベル8を出力する列が二つ残っている。
完璧とはいかないものの教師なしで正解率は85%となりました。
改善
さて、正解率を上げる為により良い$X'$を作る変換を探すのも手ですが、損失関数に一工夫することで精度を上げることにします。
先ほどの学習過程を見るに、行列$P$の周辺確率が均等になっていないことがクラスタリングミスの原因のように見える。
相互情報量の式を確認すると、$H(X), H(Y)$の項が周辺確率を均等にすることがわかります。
そこでこの項に重みalphaを付けてパラメータとすることにしました。
# alphaを加えたloss
loss = tf.math.reduce_sum(P * (alpha * tf.math.log(Pi) + alpha * tf.math.log(Pj) - tf.math.log(P)))
alphaを10にして学習した結果が以下です。

学習が安定してほぼすべてのクラスタリングが成功している。
最も高かった正解率は約97.5%であり、なかなかの精度を出すことができた。
おまけ
Overclusteringがどのような分類をしているのか気になったので確認する。
以下が最も精度を出したモデルでのOverclustering(50次元)の混合行列である。
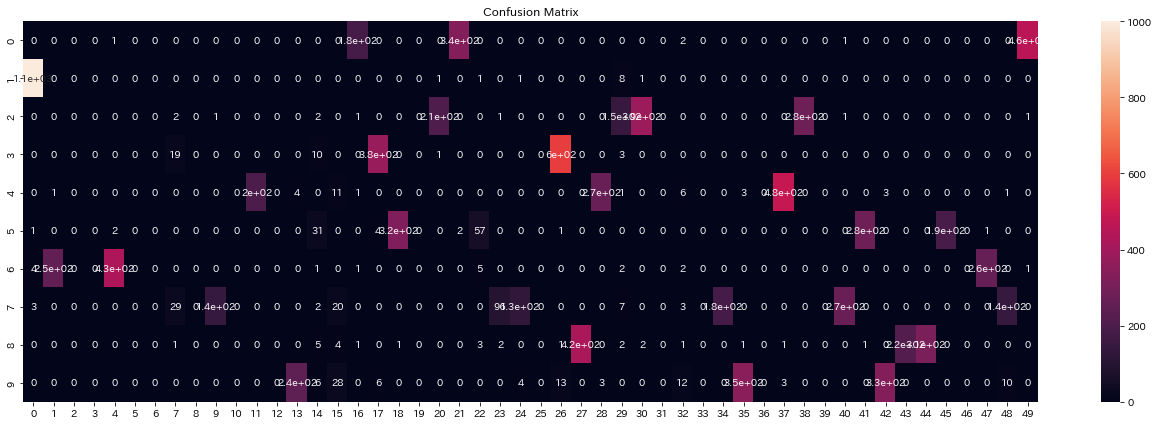
こちらもすべてのラベルを分類できていることが確認できる。
この中からラベル7の列9, 23, 40について一部を表示した。
| 列 9 | 列23 | 列40 |
 |
 |
 |
それぞれ"7"の書き方の特徴を捉えている。
列9と列40の違いは線の太さだろうか。
他の数字を調べてみても太さの違いでクラスターが分かれいることが多かったが、これは畳み込み層の性質が出ているように思えます。
注目したいのは列23である。
すべてを確認したが、個人的には見慣れない2画で書く"7"は列23にほぼ全て収まっていた。
この"7"を分類して取り出せるということは、教師データ以上のラベルを新しく作る可能性を秘めていると感じた。
IICの論文ではセグメンテーションにも適用できる手法であることが示されており、相互情報量の計算さえできれば様々なタスクに応用できるようです。
教師データの必要ないロマン性能にあふれてる手法でした。