※2018年06月23日追記
PyTorchを使用した最新版の内容を次の書籍にまとめました。
つくりながら学ぶ! 深層強化学習 ~PyTorchによる実践プログラミング~ 18年6月28日発売
「倒立振子(棒立て問題)」を、強化学習のQ学習、DQNおよびDDQN(Double DQN)で実装・解説したので、紹介します。
ディープラーニングのライブラリにはKerasを使用しました。
(※追記:17/09/27にHuber関数部分を修正しました)
(※追記:17/10/01にQ学習更新のr抜けを修正しました)
(※追記:17/10/03にQ学習報酬のrewardを修正しました)
(※追記:18/05/16にDDQNのターゲットの更新方法を修正しました)
(※追記:18/06/12にDQNのplayとDDQNのターゲットの更新方法を修正しました)
(※追記:18/10/20にDDQNの行動選択の引数がtargetQNになっていたのを、mainQNに修正しました)
概要
Open AI GymのCartPole(棒立て)をQ学習(Q-learning)、DQN(deep Q-learning)およびDDQN(Dobule DQN)で実装しました。
【対象者】
・強化学習に興味がある方
・強化学習を実装例から学びたい方
・ゼロからDeepまで学ぶ強化学習を読み、次は簡単な実装例が見たい方
・これからの強化学習(白い本)や強化学習(青い本)を読んだが、理解が難しく、簡単な実装例を知りたい方
【得られるもの】
各手法を使用したミニマム・シンプルなプログラムが実装できるようになります。
※保守性や汎用性を重視した「分かる人には扱いやすいプログラム」は書いていません。
強化学習の初学者が分かりやすいように、上から下に読んで、すんなり理解できるプログラムを書くように心がけました。
シンプルなクラス設計、関数設計にし、1ファイルでプログラムが完結しています。
コメントを多めに入れるようにしました。
※各プログラムは120行から170行程度です。
※各コードの詳細説明を掲載すると長くすぎるので、別ページに掲載しております。
棒立て、CartPoleについて
CartPoleはOpen AI Gymと呼ばれるライブラリの「棒を立て続けるタスク」です(冒頭の動画)。
子供の頃、掃除の時間に、ほうきを手のひらで立てて遊んだと思いますが、あれです。
手のひらの代わりに、Cart(車)になっています。
時刻tでの「状態s(t)」はcartの位置x、cartの速度v、棒の角度θ、棒の角速度ωの4次元で表現されます。
私たちにできる行動(Action)は、cartを右に押すか、左に押すかの2択です。
状態s(t)に応じて、適切な行動a(t)を選択し、棒を200stepの間、立て続けられたら成功です。
Open AI gymやディープラーニングのライブラリはWindowsでは使用しにくいので、Ubuntu環境をおすすめします。
私はVirtual Boxを使用したり、PCをWindowsとUbuntuのデュアルブートにしています。
強化学習について
今回やりたいことは、
状態s(t)=[x(t)、v(t)、θ(t)、ω(t)]において、適切な行動a(t)を求めることです。
Q学習、DQNについては、以下の解説が分かりやすいです。
まずはこちらを読んで、イメージをつかんでください。
上記サイトで分かりづらかった点のみ、補足的に説明します。
Q学習(Q-learning)
Q関数の表現方法
私は、Q関数の実装方法が最初よく分からなかったので、解説します。
Q学習のゴールは、正しい行動価値関数Q(s, a)を求めることです。
行動価値関数Q(s,a)は、状態sのときに行動aをした場合、その先最大で得られるであろう報酬合計R(t)を返す関数です。
※未来の報酬は、時間割引率をかけて、若干小さくなっています
Q学習では、このQ関数はテーブル(表)形式で実装されることになります。
今回、カートの位置x(t)などの状態変数は全て連続値ですが、「xは-2.4から2.4までを6分割した離散値にする」などとして、「離散化」を行います。
仮に4つの状態変数を全て6分割したとすると、6^4 = 1296 通りの状態で表されます。
Q関数は、行方向が1296、列方向は右に押すか、左に押すかの2通りで、[1296×2]の行列で表現されます。
各行列のマスの中身はQ(s,a)の値となります。
実装:CartPoleをQ学習で解く
実際にQ学習でCartPoleを実装したコードがこちらです。
100行ちょっとになります。
# coding:utf-8
# [0]ライブラリのインポート
import gym #倒立振子(cartpole)の実行環境
from gym import wrappers #gymの画像保存
import numpy as np
import time
# [1]Q関数を離散化して定義する関数 ------------
# 観測した状態を離散値にデジタル変換する
def bins(clip_min, clip_max, num):
return np.linspace(clip_min, clip_max, num + 1)[1:-1]
# 各値を離散値に変換
def digitize_state(observation):
cart_pos, cart_v, pole_angle, pole_v = observation
digitized = [
np.digitize(cart_pos, bins=bins(-2.4, 2.4, num_dizitized)),
np.digitize(cart_v, bins=bins(-3.0, 3.0, num_dizitized)),
np.digitize(pole_angle, bins=bins(-0.5, 0.5, num_dizitized)),
np.digitize(pole_v, bins=bins(-2.0, 2.0, num_dizitized))
]
return sum([x * (num_dizitized**i) for i, x in enumerate(digitized)])
# [2]行動a(t)を求める関数 -------------------------------------
def get_action(next_state, episode):
#徐々に最適行動のみをとる、ε-greedy法
epsilon = 0.5 * (1 / (episode + 1))
if epsilon <= np.random.uniform(0, 1):
next_action = np.argmax(q_table[next_state])
else:
next_action = np.random.choice([0, 1])
return next_action
# [3]Qテーブルを更新する関数 -------------------------------------
def update_Qtable(q_table, state, action, reward, next_state):
gamma = 0.99
alpha = 0.5
next_Max_Q=max(q_table[next_state][0],q_table[next_state][1] )
q_table[state, action] = (1 - alpha) * q_table[state, action] +\
alpha * (reward + gamma * next_Max_Q)
return q_table
# [4]. メイン関数開始 パラメータ設定--------------------------------------------------------
env = gym.make('CartPole-v0')
max_number_of_steps = 200 #1試行のstep数
num_consecutive_iterations = 100 #学習完了評価に使用する平均試行回数
num_episodes = 2000 #総試行回数
goal_average_reward = 195 #この報酬を超えると学習終了(中心への制御なし)
# 状態を6分割^(4変数)にデジタル変換してQ関数(表)を作成
num_dizitized = 6 #分割数
q_table = np.random.uniform(
low=-1, high=1, size=(num_dizitized**4, env.action_space.n))
total_reward_vec = np.zeros(num_consecutive_iterations) #各試行の報酬を格納
final_x = np.zeros((num_episodes, 1)) #学習後、各試行のt=200でのxの位置を格納
islearned = 0 #学習が終わったフラグ
isrender = 0 #描画フラグ
# [5] メインルーチン--------------------------------------------------
for episode in range(num_episodes): #試行数分繰り返す
# 環境の初期化
observation = env.reset()
state = digitize_state(observation)
action = np.argmax(q_table[state])
episode_reward = 0
for t in range(max_number_of_steps): #1試行のループ
if islearned == 1: #学習終了したらcartPoleを描画する
env.render()
time.sleep(0.1)
print (observation[0]) #カートのx位置を出力
# 行動a_tの実行により、s_{t+1}, r_{t}などを計算する
observation, reward, done, info = env.step(action)
# 報酬を設定し与える
if done:
if t < 195:
reward = -200 #こけたら罰則
else:
reward = 1 #立ったまま終了時は罰則はなし
else:
reward = 1 #各ステップで立ってたら報酬追加
episode_reward += reward #報酬を追加
# 離散状態s_{t+1}を求め、Q関数を更新する
next_state = digitize_state(observation) #t+1での観測状態を、離散値に変換
q_table = update_Qtable(q_table, state, action, reward, next_state)
# 次の行動a_{t+1}を求める
action = get_action(next_state, episode) # a_{t+1}
state = next_state
#終了時の処理
if done:
print('%d Episode finished after %f time steps / mean %f' %
(episode, t + 1, total_reward_vec.mean()))
total_reward_vec = np.hstack((total_reward_vec[1:],
episode_reward)) #報酬を記録
if islearned == 1: #学習終わってたら最終のx座標を格納
final_x[episode, 0] = observation[0]
break
if (total_reward_vec.mean() >=
goal_average_reward): # 直近の100エピソードが規定報酬以上であれば成功
print('Episode %d train agent successfuly!' % episode)
islearned = 1
#np.savetxt('learned_Q_table.csv',q_table, delimiter=",") #Qtableの保存する場合
if isrender == 0:
#env = wrappers.Monitor(env, './movie/cartpole-experiment-1') #動画保存する場合
isrender = 1
#10エピソードだけでどんな挙動になるのか見たかったら、以下のコメントを外す
#if episode>10:
# if isrender == 0:
# env = wrappers.Monitor(env, './movie/cartpole-experiment-1') #動画保存する場合
# isrender = 1
# islearned=1;
if islearned:
np.savetxt('final_x.csv', final_x, delimiter=",")
実行結果の一例は以下の通りです。
100試行ほどで、立ちますが、どっか行ってしまいます。
(子供がホウキ立てをやってるときに似ていて興味深い)
1000試行ほどで、200step立てるようになります。
「Q学習の詳細な説明」および、「掲載したコードの詳細な解説」はこちらを御覧ください。
●CartPoleでQ学習(Q-learning)を実装・解説【Phythonで強化学習:第1回】
DQN
DQNはQ学習のQ関数をDL(ディープラーニング)で表した方法です。
やはりまずはこちらを読んで、イメージをつかんでください。
また、こちらの新しい本にも、最新の強化学習を紹介する章が用意されており、DNQやDDQNからA3Cまで説明があります。
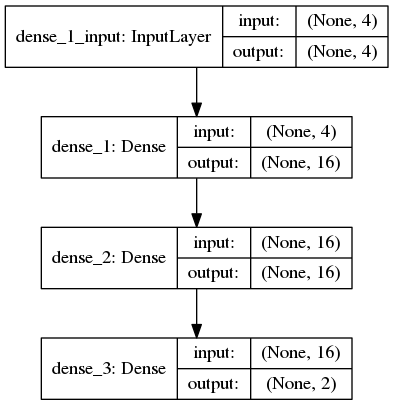
Qネットワーク
Q関数をディープニューラルネットワークで表したQネットワークについて説明します。
入力層のニューロン数は、状態の次元数となります。
今回であれば、cartの位置x、cartの速度v、棒の角度θ、棒の角速度ωの4つです。
状態の値をそのまま入力層の素子に与えます。
Q学習とは異なり、離散化はしません。
連続値をそのまま入力します。
出力層のニューロン数は、選択できる行動の数となります。
今回であれば、右か左の2つです。
そして出力ニューロンが出力する値は、「右に押すニューロン」であれば、Q(s(t), 右)の値です。
状態s(t)のときにa(t) = 右に押す
を行った場合に、その先に得られる報酬の総計が出力されます。
今回の例ですと以下のようなネットワークを使用します。
Qネットワークの学習
Qネットワークの重みを変化させて、より良いQネットワークを実現します。
状態s(t)でa(t)=右に押す の場合、Qネットワークの出力層、右ニューロンはQ(s(t), 右)という値を出力します。
時刻tの時点で出力してほしいのは、r(t)+γ・MAX[Q(s_{t+1}, a_{t+1})]です。
※この教師信号も本当は学習途中です
※r(t)は時刻tでもらう報酬、γは時間割引率
Q(s(t), 右)= r(t)+γ・MAX[Q(s_{t+1}, a_{t+1})]
となれば、学習は終了していることになります。
この、Q(s(t), 右に押す)と r(t)+γ・MAX[Q(s_{t+1}, a_{t+1})]の差が小さくなる方向にQネットワークの重みを更新します。
DQN特有の4つの工夫
DQNは単純にQ関数をDL(ディープラーニング)にする以外に、4つの工夫があります。
こちらのページが分かりやすいので、まずイメージをつかんでください。
●DQNをKerasとTensorFlowとOpenAI Gymで実装する
1つ目の工夫Experience Replayは、学習内容をメモリに保存して、ランダムにとりだして学習します。
2つ目の工夫Fixed Target Q-Networkは、1step分ずつ学習するのでなく、複数ステップ分をまとめて学習(バッチ学習)します。
3つ目の工夫報酬のclippingは、各ステップでの報酬を-1から1の間にします。
今回は各ステップで立っていたら報酬0、こけたら報酬-1、195 step以上立って終了したら報酬+1とクリップしました。
4つ目の誤差関数の工夫は、誤差が1以上では二乗誤差でなく絶対値誤差を使用するHuber関数を実装します。
DDQN
DDQN(Double DQN)は行動価値関数Qを、価値と行動を計算するメインのQmainと、MAX[Q(s_{t+1}, a_{t+1})]を評価するQtargetに分ける方法です。
分けることで、Q関数の誤差が増大するのを防ぎます。
今回は、試行ごとにQtargetを更新することでDDQNを実現しました。
各試行ではQtargetはひとつ前の試行のQmainの最終値を使用します。
DQN、DDQNの実装
実装したコードがこちらです。
DQN、DDQNは同じファイルです。
途中のDQN_MODEという変数で切り替えています。
# coding:utf-8
# [0]必要なライブラリのインポート
import gym # 倒立振子(cartpole)の実行環境
import numpy as np
import time
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
from keras.utils import plot_model
from collections import deque
from gym import wrappers # gymの画像保存
from keras import backend as K
import tensorflow as tf
# [1]損失関数の定義
# 損失関数にhuber関数を使用します 参考https://github.com/jaara/AI-blog/blob/master/CartPole-DQN.py
def huberloss(y_true, y_pred):
err = y_true - y_pred
cond = K.abs(err) < 1.0
L2 = 0.5 * K.square(err)
L1 = (K.abs(err) - 0.5)
loss = tf.where(cond, L2, L1) # Keras does not cover where function in tensorflow :-(
return K.mean(loss)
# [2]Q関数をディープラーニングのネットワークをクラスとして定義
class QNetwork:
def __init__(self, learning_rate=0.01, state_size=4, action_size=2, hidden_size=10):
self.model = Sequential()
self.model.add(Dense(hidden_size, activation='relu', input_dim=state_size))
self.model.add(Dense(hidden_size, activation='relu'))
self.model.add(Dense(action_size, activation='linear'))
self.optimizer = Adam(lr=learning_rate) # 誤差を減らす学習方法はAdam
# self.model.compile(loss='mse', optimizer=self.optimizer)
self.model.compile(loss=huberloss, optimizer=self.optimizer)
# 重みの学習
def replay(self, memory, batch_size, gamma, targetQN):
inputs = np.zeros((batch_size, 4))
targets = np.zeros((batch_size, 2))
mini_batch = memory.sample(batch_size)
for i, (state_b, action_b, reward_b, next_state_b) in enumerate(mini_batch):
inputs[i:i + 1] = state_b
target = reward_b
if not (next_state_b == np.zeros(state_b.shape)).all(axis=1):
# 価値計算(DDQNにも対応できるように、行動決定のQネットワークと価値観数のQネットワークは分離)
retmainQs = self.model.predict(next_state_b)[0]
next_action = np.argmax(retmainQs) # 最大の報酬を返す行動を選択する
target = reward_b + gamma * targetQN.model.predict(next_state_b)[0][next_action]
targets[i] = self.model.predict(state_b) # Qネットワークの出力
targets[i][action_b] = target # 教師信号
# shiglayさんよりアドバイスいただき、for文の外へ修正しました
self.model.fit(inputs, targets, epochs=1, verbose=0) # epochsは訓練データの反復回数、verbose=0は表示なしの設定
# [3]Experience ReplayとFixed Target Q-Networkを実現するメモリクラス
class Memory:
def __init__(self, max_size=1000):
self.buffer = deque(maxlen=max_size)
def add(self, experience):
self.buffer.append(experience)
def sample(self, batch_size):
idx = np.random.choice(np.arange(len(self.buffer)), size=batch_size, replace=False)
return [self.buffer[ii] for ii in idx]
def len(self):
return len(self.buffer)
# [4]カートの状態に応じて、行動を決定するクラス
# アドバイスいただき、引数にtargetQNを使用していたのをmainQNに修正しました
class Actor:
def get_action(self, state, episode, mainQN): # [C]t+1での行動を返す
# 徐々に最適行動のみをとる、ε-greedy法
epsilon = 0.001 + 0.9 / (1.0+episode)
if epsilon <= np.random.uniform(0, 1):
retTargetQs = mainQN.model.predict(state)[0]
action = np.argmax(retTargetQs) # 最大の報酬を返す行動を選択する
else:
action = np.random.choice([0, 1]) # ランダムに行動する
return action
# [5] メイン関数開始----------------------------------------------------
# [5.1] 初期設定--------------------------------------------------------
DQN_MODE = 1 # 1がDQN、0がDDQNです
LENDER_MODE = 1 # 0は学習後も描画なし、1は学習終了後に描画する
env = gym.make('CartPole-v0')
num_episodes = 299 # 総試行回数
max_number_of_steps = 200 # 1試行のstep数
goal_average_reward = 195 # この報酬を超えると学習終了
num_consecutive_iterations = 10 # 学習完了評価の平均計算を行う試行回数
total_reward_vec = np.zeros(num_consecutive_iterations) # 各試行の報酬を格納
gamma = 0.99 # 割引係数
islearned = 0 # 学習が終わったフラグ
isrender = 0 # 描画フラグ
# ---
hidden_size = 16 # Q-networkの隠れ層のニューロンの数
learning_rate = 0.00001 # Q-networkの学習係数
memory_size = 10000 # バッファーメモリの大きさ
batch_size = 32 # Q-networkを更新するバッチの大記載
# [5.2]Qネットワークとメモリ、Actorの生成--------------------------------------------------------
mainQN = QNetwork(hidden_size=hidden_size, learning_rate=learning_rate) # メインのQネットワーク
targetQN = QNetwork(hidden_size=hidden_size, learning_rate=learning_rate) # 価値を計算するQネットワーク
# plot_model(mainQN.model, to_file='Qnetwork.png', show_shapes=True) # Qネットワークの可視化
memory = Memory(max_size=memory_size)
actor = Actor()
# [5.3]メインルーチン--------------------------------------------------------
for episode in range(num_episodes): # 試行数分繰り返す
env.reset() # cartPoleの環境初期化
state, reward, done, _ = env.step(env.action_space.sample()) # 1step目は適当な行動をとる
state = np.reshape(state, [1, 4]) # list型のstateを、1行4列の行列に変換
episode_reward = 0
# 2018.05.16
# skanmeraさんより間違いを修正いただきました
# targetQN = mainQN # 行動決定と価値計算のQネットワークをおなじにする
# ↓
targetQN.model.set_weights(mainQN.model.get_weights())
for t in range(max_number_of_steps + 1): # 1試行のループ
if (islearned == 1) and LENDER_MODE: # 学習終了したらcartPoleを描画する
env.render()
time.sleep(0.1)
print(state[0, 0]) # カートのx位置を出力するならコメントはずす
action = actor.get_action(state, episode, mainQN) # 時刻tでの行動を決定する
next_state, reward, done, info = env.step(action) # 行動a_tの実行による、s_{t+1}, _R{t}を計算する
next_state = np.reshape(next_state, [1, 4]) # list型のstateを、1行4列の行列に変換
# 報酬を設定し、与える
if done:
next_state = np.zeros(state.shape) # 次の状態s_{t+1}はない
if t < 195:
reward = -1 # 報酬クリッピング、報酬は1, 0, -1に固定
else:
reward = 1 # 立ったまま195step超えて終了時は報酬
else:
reward = 0 # 各ステップで立ってたら報酬追加(はじめからrewardに1が入っているが、明示的に表す)
episode_reward += 1 # reward # 合計報酬を更新
memory.add((state, action, reward, next_state)) # メモリの更新する
state = next_state # 状態更新
# Qネットワークの重みを学習・更新する replay
if (memory.len() > batch_size) and not islearned:
mainQN.replay(memory, batch_size, gamma, targetQN)
if DQN_MODE:
# 2018.06.12
# shiglayさんさんより間違いを修正いただきました
# targetQN = mainQN # 行動決定と価値計算のQネットワークをおなじにする
# ↓
targetQN.model.set_weights(mainQN.model.get_weights())
# 1施行終了時の処理
if done:
total_reward_vec = np.hstack((total_reward_vec[1:], episode_reward)) # 報酬を記録
print('%d Episode finished after %f time steps / mean %f' % (episode, t + 1, total_reward_vec.mean()))
break
# 複数施行の平均報酬で終了を判断
if total_reward_vec.mean() >= goal_average_reward:
print('Episode %d train agent successfuly!' % episode)
islearned = 1
if isrender == 0: # 学習済みフラグを更新
isrender = 1
# env = wrappers.Monitor(env, './movie/cartpoleDDQN') # 動画保存する場合
# 10エピソードだけでどんな挙動になるのか見たかったら、以下のコメントを外す
# if episode>10:
# if isrender == 0:
# env = wrappers.Monitor(env, './movie/cartpole-experiment-1') #動画保存する場合
# isrender = 1
# islearned=1;
実行結果の一例は以下の通りです。
100試行ほどで、200step立てるようになります。
Q学習のときは学習に1000試行かかりましたが、DQN、DDQNは1/10の100試行ほどで立てるようになりました。
DQNよりDDQNの方が収束が早い気がします。
DQN
DDQN
「DQN、DDQNの詳細な説明」および、「掲載したコードの詳細な解説」はこちらを御覧ください。
●CartPoleでDQN(deep Q-learning)、DDQNを実装・解説【Phythonで強化学習:第2回】
以上、CartPoleでQ学習、DQN、DDQNをシンプルに実装する方法を紹介しました。
強化学習の実装イメージを持ってもらえれば幸いです。
次回はディープラーニングを用いたより発展的な強化学習である
dueling network、prioritized experience replay、A3C
あたりを実装する予定です。
しばしお待ち下さい。
以上、ご一読いただき、ありがとうございました。