どうも!
Atraeのデータサイエンティスト(ワナビ)の杉山です!
今日は、先日社内の勉強会で話題になった「なぜ最小二乗法なのか」についてまとめます。
回帰分析の話で話題になったのですが、回帰分析の説明するには余白が足りないので、それはこちらに譲ります!
回帰分析自体についてはこちら→単回帰分析とは | データ分析基礎知識
※二乗と2乗で表記が揺れまくりますが、許してください、なんでもしますから!
簡単のため、単回帰分析の場合で考えます。
2種の変量$x, y$に対して、データ$x_i, y_i , (1 \leq i \leq N)$があったとします。
$y = ax + b$の式を用いて回帰分析をかけるとしましょう。
ここでやりたいのは、何らかの基準で、最も良い$a, b$を選ぶことです。
(こんご、選ばれた$a, b$のことを$\hat{a}, \hat{b}$と書くことにします。これを、推定量と言います。)
基準としてよく選ばれるのは、誤差の2乗和
$$E = \sum_i (y_i - (ax_i + b))^2$$
を最小化する$\hat{a}, \hat{b}$を探す最小二乗法です。
では、なぜ最小二乗法なのでしょうか?
僕が思いつく限りでは、理由は以下の5つです。
- 計算が簡単だから
- 計算の意味が明瞭だから
- 最良線形不偏推定量(BLUE)を与えるから
- 最尤推定から導かれる計算法だから
- 幾何学的な意味付けがあるから
(今回のアドベントカレンダーでは3記事しか書かないのですが、勝手に5記事書いてみようかと思いますw)
計算が簡単だから
今回、「誤差を最小」にするという方針で$a, b$を選ぼうという話でした。
2乗を選ぶのは、プラスマイナスで打ち消さないために2乗を使うという説明もありますが、普通に考えたら、誤差の絶対値和
$$E_1 = \sum_i \big|y_i - (ax_i + b)\big|$$
の最小化でもいいかもしれないし、4乗、6乗、8乗…
E_4 = \sum_i (y_i - (ax_i + b))^4 \\
E_6 = \sum_i (y_i - (ax_i + b))^6 \\
E_8 = \sum_i (y_i - (ax_i + b))^8
でもいいかもしれません。
それぞれを最小にする推定量$\hat{a}, \hat{b}$を計算してみながら、なぜ最小二乗がよいのかを考えたいと思います。
最小2乗の場合
まず、最小2乗法についてやっておきましょう。
\begin{align}
E &= \sum_i (y_i - (ax_i + b))^2
\end{align}
にたいして、それを最小にする$\hat{a}, \hat{b}$を探しましょう。
$E$を$a, b$の関数と思うと、$a, b$の2次関数になります。
(ちゃんと書くと$E = A a^2 + B ab + C b^2 + D a + F b + G$の形になります。各ギリシャ文字は、$A = \sum_i x_i^2, B = 2 \sum_i x_i, C = N$(データ数)$, D = -2 \sum_i x_i y_i, F = -2\sum_i y_i, G = \sum_i y_i^2$です。大事なのは式の形ではなく、「データがあればA~Gを決められる」、「Eは所詮2次関数」という点です。)
(下に凸な)2次関数の最小化は、微分が0になる点を求めれば完了するので、それを求めてみます。
\begin{align}
& \partial_a E \left(:= \frac{\partial E}{\partial a} \right) = 0 \\
& \Leftrightarrow \frac\partial{\partial a} \sum_i (y_i - (ax_i + b))^2 = 0 \\
& \Leftrightarrow \sum_i \frac\partial{\partial a}(y_i - (ax_i + b))^2 = 0\\
& \Leftrightarrow \sum_i -2 x_i (y_i - (ax_i + b)) = 0 \dots (1)
\end{align}
次はbで微分。
\begin{align}
& \partial_b E = 0 \\
& \Leftrightarrow \frac\partial{\partial b} \sum_i (y_i - (ax_i + b))^2 = 0 \\
& \Leftrightarrow \sum_i \frac\partial{\partial b}(y_i - (ax_i + b))^2 = 0\\
& \Leftrightarrow \sum_i -2(y_i - (ax_i + b)) = 0 \dots (2)
\end{align}
これは、所詮$a, b$に関する連立一次方程式なので、やれば解けます。
で、
\begin{align}
\hat{a} &= \frac{\text{cov}(x, y)}{V[x]} \\
\hat{b} &= E[y] - \frac{\text{cov}(x, y)}{V[x]}E[x]
\end{align}
となります。
(※$V[x]$は$x$の分散、$\text{cov}(x, y)$は$x, y$の共分散、$E[x]$は$x$の平均です。)
ポイントは、
- 閉じた形で解が求まる(= 公式が作れる)
- 1次方程式解けばいい
です。
覚えておいて下さい。
最小4乗の場合
同じことを試みてみます!
\begin{align}
E_4 = \sum_i (y_i - (ax_i + b))^4
\end{align}
これの最小化をします。
一般の4次関数は、微分=0を解いただけではダメですが、今回の場合も都合がいいことに微分=0と最小値を与えるという2条件が同値なので、その方針で解きます。
(※$E_4$は$a, b$に関する凸関数$(y_i - (ax_i + b))$の和なので$a, b$に関して凸関数になるからです。)
\begin{align}
& \partial_a E_4 = 0 \\
& \Leftrightarrow \frac\partial{\partial a} \sum_i (y_i - (ax_i + b))^4 = 0 \\
& \Leftrightarrow \sum_i \frac\partial{\partial a}(y_i - (ax_i + b))^4 = 0\\
& \Leftrightarrow \sum_i -4 x_i (y_i - (ax_i + b))^3 = 0 \dots (3)
\end{align}
次はbで微分。
\begin{align}
& \partial_b E_4 = 0 \\
& \Leftrightarrow \frac\partial{\partial b} \sum_i (y_i - (ax_i + b))^4 = 0 \\
& \Leftrightarrow \sum_i \frac\partial{\partial b}(y_i - (ax_i + b))^4 = 0\\
& \Leftrightarrow \sum_i -4(y_i - (ax_i + b))^3 = 0 \dots (4)
\end{align}
$a, b$に関する連立方程式$(3), (4)$を解けばいいのですが。
と、解けません…。
(3)を満たす点と(4)を満たす点を曲線として書いてみると、こんな感じです。たぶん。
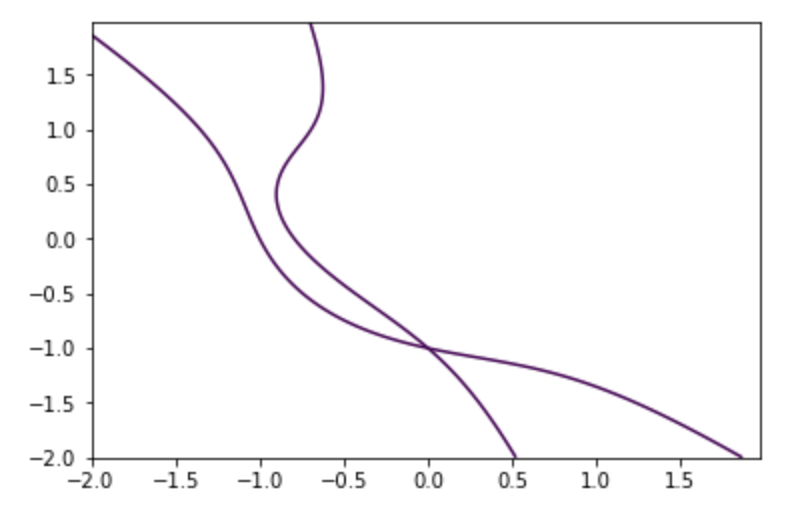
こんな感じの3次曲線の交点を求めることになります。
ですので、$\hat{a}, \hat{b}$を求めるには、この時点で数値計算にかける必要があります。
先ほどと比較すると、
- 閉じた形で解が求らない
- 数値計算の必要があるので計算が重い(たぶん)
- 求まらないので、あれこれ今後の議論するのが大変
- 3次方程式解かなあかん
- たいへん
- っていうか無理
うーん。やっぱり2乗がいいですね。
絶対値
まず、はじめに言います。
絶対値が含まれる関数の最小化はヤバイ。
大事なことなのでもう一度言います。
絶対値が含まれる関数の最小化はホントマジでヤバイ。
見ていきましょう。
$$E_1 = \sum_i \big|y_i - (ax_i + b)\big|$$
こいつの最小化を考えるのは難しいので、まず、$a$に関する1変数関数の最小化を考えてみましょう。
\begin{align}
f_1(a) &= |a| \\
f_2(a) &= |a+1| + |a-1| \\
f_3(a) &= |a+2| + |a-1| + |a-2|
\end{align}
3つのグラフを書いてみます。
$f_1(a)$の場合、
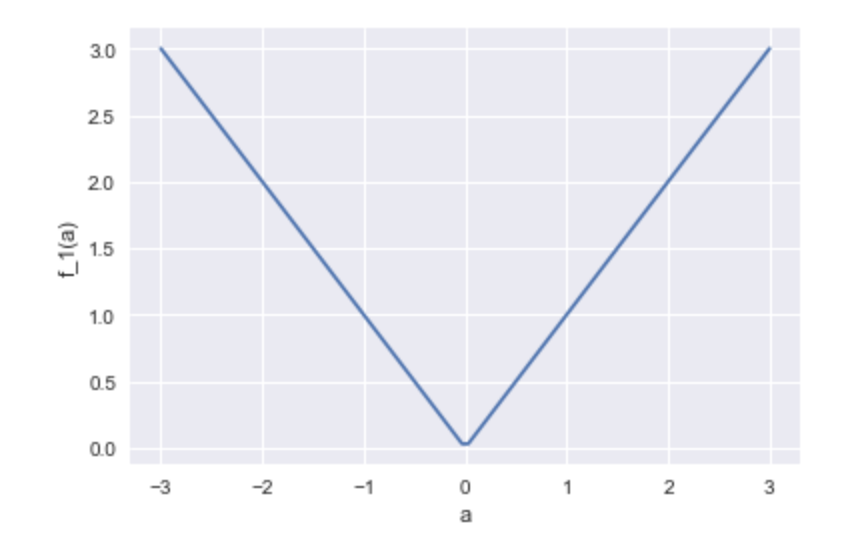
こうなります。
式を見てもわかりますが、$\hat{a}=0$です。
$f_2(a)$の場合、
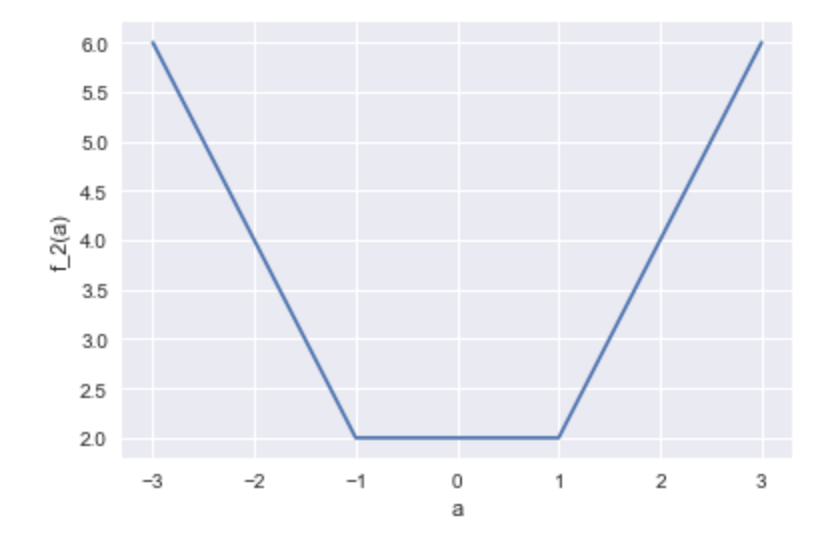
こうなります。
事件です!このとき、-1以上1以下の全ての$a$が最小値を与えます。ですので、どれか選ぶ必要があります。困った。
最小2乗や最小4乗の場合、こういうことは起こらず、必ず最小値は一意なのですが(※$E$や$E_4$は狭義凸関数なので)、絶対値を用いる場合、こういうことが起こります。
とりあえず、中間の値を推定値として選ぶことにして、$\hat{a} = 0$ということにしておきましょう。
$f_3(a)$の場合、
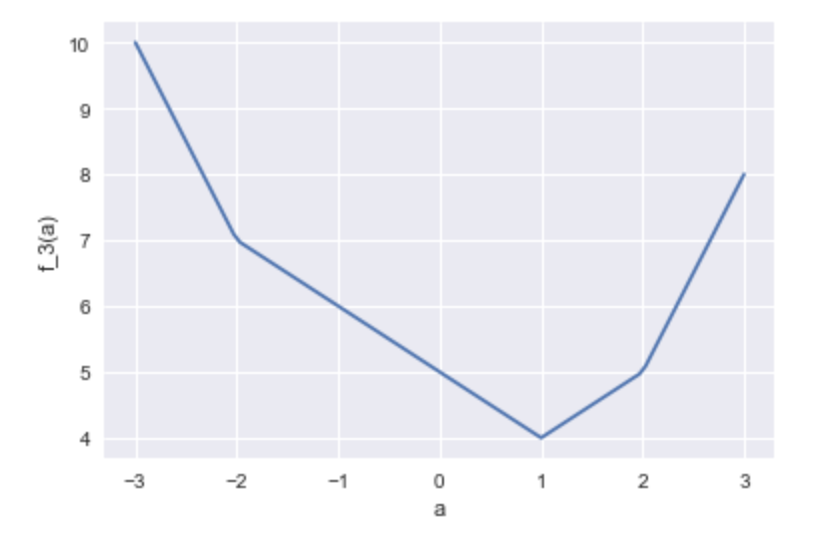
こうなります。今度は$\hat{a} = 1$となります。
ちなみに、一般に、今の戦略で$f_N(a) = \sum_i |a-x_i|$の最小値を求めると、$\hat{a}$は$x$の中央値を選ぶことになります。
「中央値」というのがわかるので、公式に近いものが得られているとはいえますね。
さてさて。
では、$a, b$の2変数の最小化に取り掛かるとしましょう。
はっきり言って、絶対値の個数が増えると地獄なので、今回は、
$g(a, b) = |a| + |b| + |a+b-1|$の最小化を考えることにします。
($E_1$がこの式になることはないですが、2変数の最小化を考えるという意味では同じなのでこれで。)
これは、次のステップで行います。
- $a$の正負、$b$の正負、$a+b-1$の正負で場合分けし、各領域での$g(a, b)$の式を求める
- 各領域での最小値を求める
- 全体での最小値を求める
やってみます。
3つの式それぞれの正負で分類すると、下の図のように、$a, b$平面が全部で7つの領域に分かれることになります。

それぞれでの$g(a, b)$の式を書いてみると、次のようになります。

うげげ。
さて、真面目に最小値を与える$a, b$を探すと、実は、中央の三角の部分全体が最小値を与える$a, b$になっていることがわかります。(気が向いたら確かめて下さい。気が向かなかったら信じて下さい)
またまた最小値が複数点で与えられてしまうんですね。困った。
前回と同じ考えで、その三角形の重心を答えとすることにすると。$\displaystyle \hat{a} = \frac13, \hat{b} = \frac13$がこたえになります。
やばさ、伝わりました?
これ、絶対値の個数が増えると、その個数分の直線を引くことになり、その各領域での関数を求め、その最小値を、、、、うげげげげ。
やりたくないですね。
※ちなみに、simplex法という数値解析手法があります。ありますが、結局、数値解析に頼ることになるので、最小4乗法のときと同じ困難に当たることになります。
これだけではなくて、今回の絶対値で作った誤差関数$E_1$の最小化は、次の2つの大きな問題を抱えることになります。
- 推定量の不連続性
- 極端な値を選ぶ傾向があること
見ていきましょう。
推定量の不連続性
先程の$g(a, b)$を少し変形して、次の3つの関数の最小化を考えます。
\begin{align}
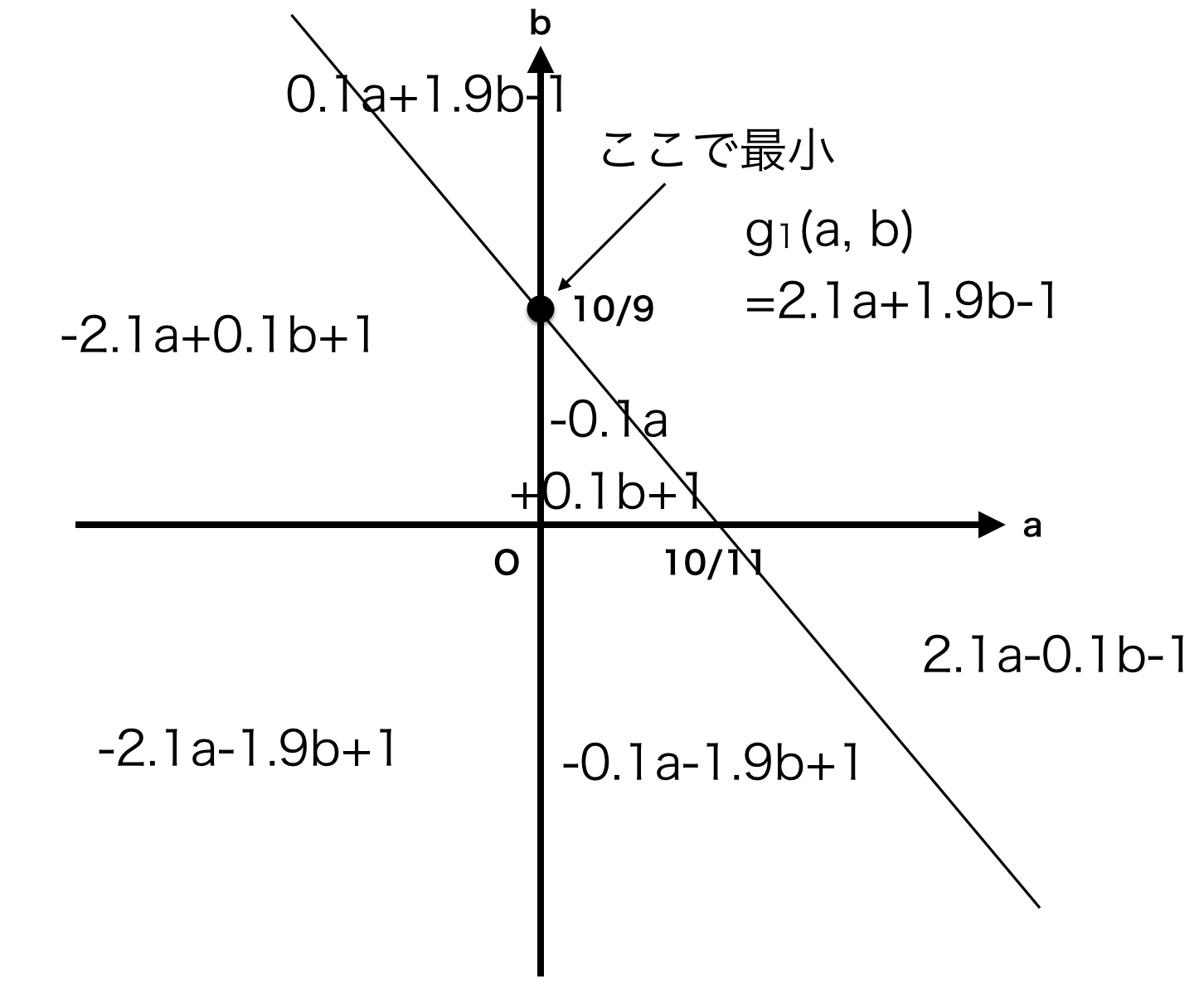
g_1(a, b) = |a| + |b| + |1.1a + 0.9b -1| \\
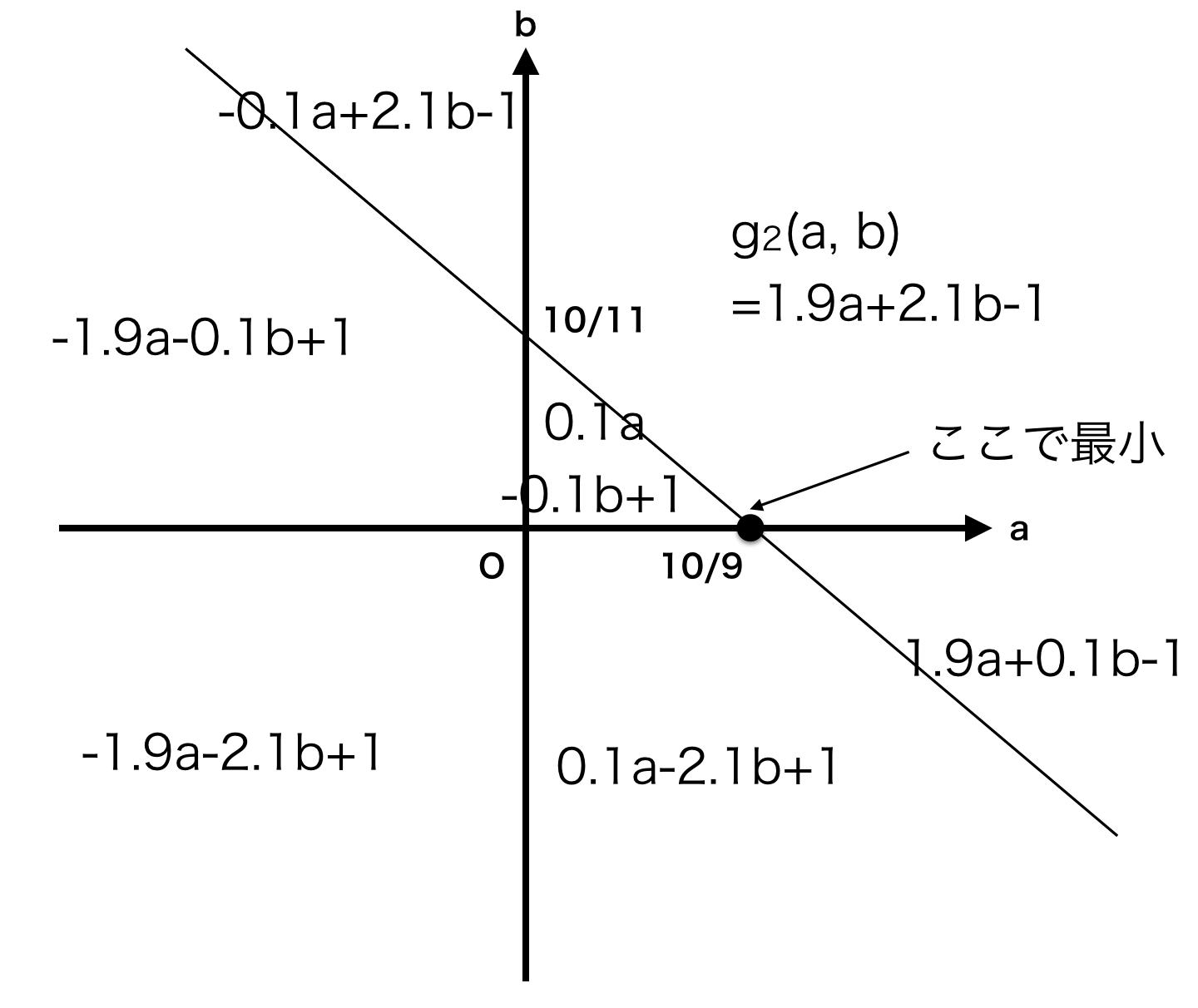
g_2(a, b) = |a| + |b| + |0.9a + 1.1b -1| \\
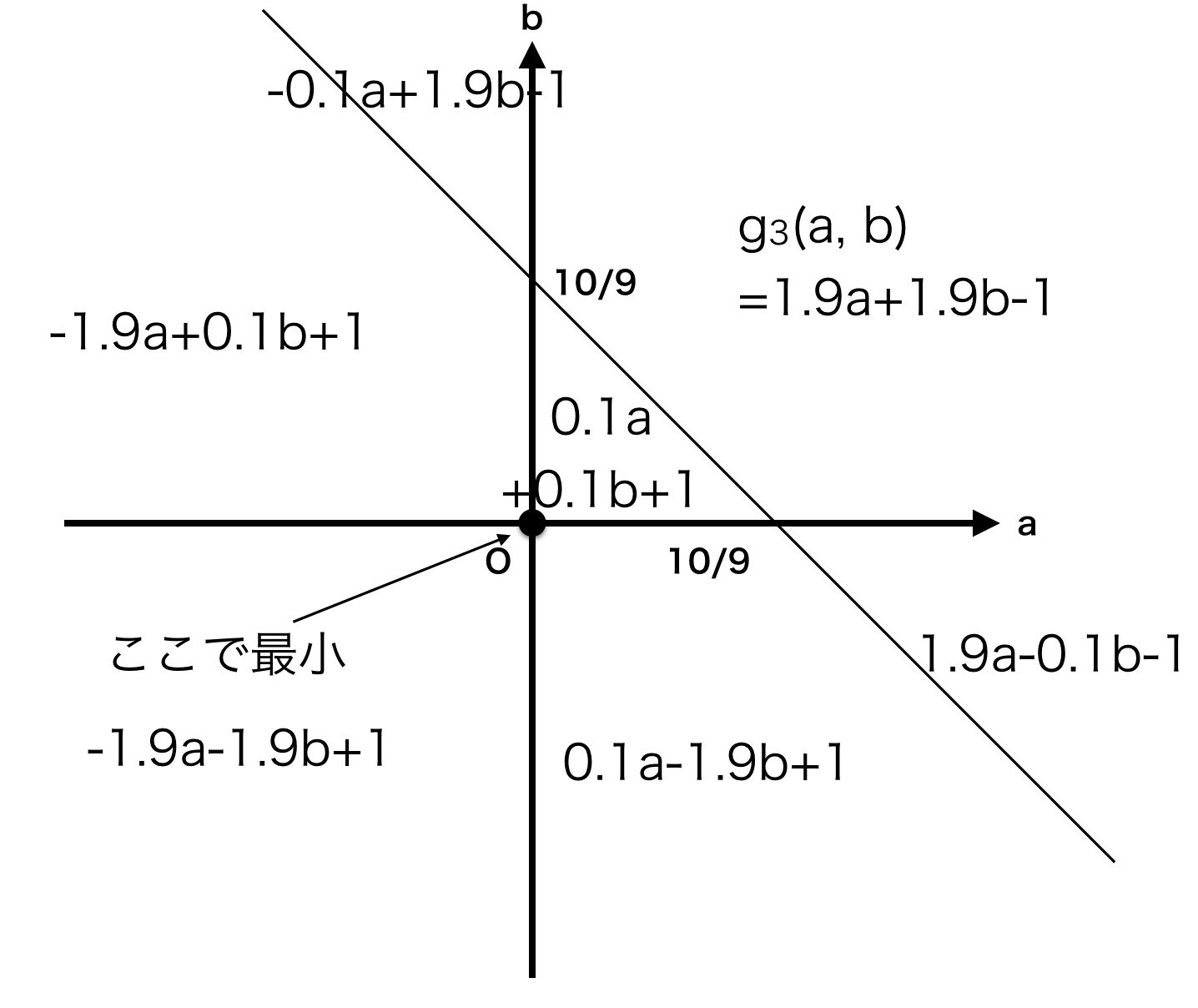
g_3(a, b) = |a| + |b| + |0.9a + 0.9b -1|
\end{align}
最小値を与える点をそれぞれ求めると、次の図のようになります。
$g_1(a, b)$の最小値は、$\displaystyle a = 0, b = \frac{10}9$
$g_2(a, b)$の最小値は、$\displaystyle a = \frac{10}9, b = 0$
$g_3(a, b)$の最小値は、$\displaystyle a = 0, b = 0$
まとめるとこうなります。
(関数→推定量$(\hat{a}, \hat{b})$という書き方です)
\begin{align}
g(a, b) = |a| + |b| + |1.0a + 1.0b -1| &\to \left( \hat{a}, \hat{b} \right) = \left(\frac13, \frac13 \right) \\
g_1(a, b) = |a| + |b| + |1.1a + 0.9b -1| &\to \left( \hat{a}, \hat{b} \right) = \left(0, \frac{10}9 \right) \\
g_2(a, b) = |a| + |b| + |0.9a + 1.1b -1| &\to \left( \hat{a}, \hat{b} \right) = \left(\frac{10}9, 0 \right) \\
g_3(a, b) = |a| + |b| + |0.9a + 0.9b -1| &\to \left( \hat{a}, \hat{b} \right) = (0, 0) \\
\end{align}
3つめの式を僅かに変えただけなのに、推定量$\hat{a}, \hat{b}$が大きく変わります。
実際、3つめの式を$|Aa+Bb-1|$と書いたとき、$A, B$が$1$の付近では、推定量$\hat{a}, \hat{b}$が不連続的に変化します。
これは困ったもので、僅かな誤差で大きく推定値が変わってしまうので、誤差というものに対してかなりセンシティブに扱わなければならなくなります。それは結構めんどくさいですね。
極端な値を選ぶ傾向があること
気づいた方もいるかもしれませんが、推定量$\hat{a}, \hat{b}$はどれかの絶対値の中身が$0$になる$a, b$であります。
たとえば、与えられたデータが$(x_1, y_1) = (-1, 1), (x_2, y_2) = (0, -1), (x_3, y_3) = (1, 1)$であったばあい、$E_1$からもとめる推定量は$\hat{a} = 0, \hat{b} = 1$になります。
グラフに書いてみると、
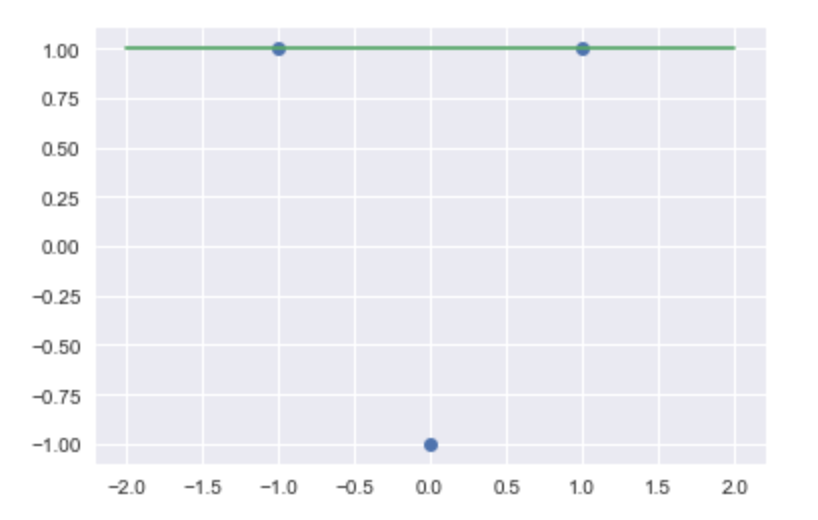
こんな感じです。
2番めのデータをガン無視していますね。。。
(データ点が3点の場合、だいたい、3つのうち2つを選んでそれを結んだ直線を選ぶことになります)
この、データを無視する傾向、$f_N(a) = \sum_i |a-x_i|$の最小値を求めるときにも見えていました。このときは、$\hat{a}$が$x$の中央値のときに最小になるのですが、中央値というのは、値の順序と、中央のものの値だけしか見ていないものです。
絶対値での最小化はこのように、データのごく一部のみを見て答えを出す性質があるのです。
まとめ
- 最小2乗法はすごい!
- 閉じた形で推定量$\hat{a}, \hat{b}$が計算できる(公式を作れる)
- 1次方程式を解くだけでいい
- 最小4乗法は…
- 数値計算しないと推定量$\hat{a}, \hat{b}$が計算できない
- 連立3次方程式を解く必要がある。やばい
- 絶対値のやつは
- 数値計算しないと推定量$\hat{a}, \hat{b}$が計算できない
- 推定量の不連続性がある
- 極端な値を選ぶ時がある
結論
最小2乗法はいいぞ!
つづき
あと4つ、最小2乗法ちゃんが素敵な理由があるんですよ。
そのうち書きます。書き切れるのかこの分量で。
乞うご期待!