前回: https://qiita.com/students/items/19d32927eace91a8d779
チートシートなのにその2は意味がわからないですが、続けます
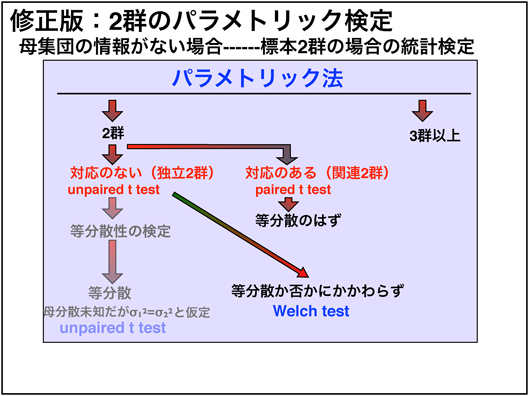
2群のパラメトリック検定
本当は対応がない2群のデータでは等分散性の検定(F検定)を行い、そこから考えるという考えがデフォルトなのですが、この等分散性はnが小さい場合には等分散であると誤認されてしまう場合が多く、一般にはn=30以上が必要とされています。対応がある場合は等分散のはずなので、検定せずに個体差を消す処理をしたあとにunpaired ttestをすればいいのですが。
まぁ、両方に適用可能なWelchのt検定を行ったほうがアンパイですね。(まだ広く認められてはいない流れらしいのでここらへんは人によるのかもしれないです)
pythonでの検定方法
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=500)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=500)
# unpaired welch's T input -> arr1,arr2
stats.ttest_ind(rvs1, rvs2, equal_var=False)
# only p-value
stats.ttest_ind(rvs1, rvs2, equal_var=False).pvalue
出力
Ttest_indResult(statistic=-0.6171876615346301, pvalue=0.5373096289461834)
0.5373096289461834
対応ありWelchのt検定
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=500)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=500)
# paired welch's T : input -> arr1,arr2
stats.ttest_rel(rvs1, rvs2)
# only p-value
stats.ttest_rel(rvs1, rvs2).pvalue
出力
Ttest_relResult(statistic=0.17370496946736086, pvalue=0.8621677749575104)
0.8621677749575104
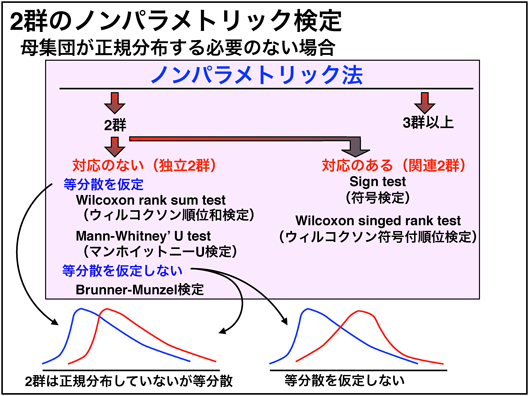
2群のノンパラメトリック検定
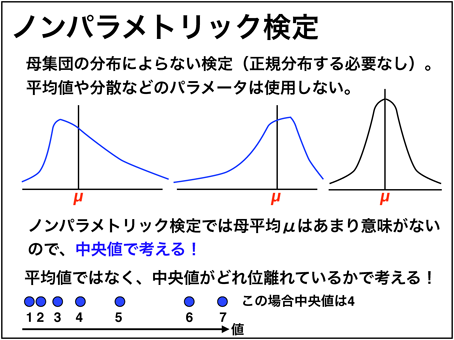
ノンパラメトリック検定は、平均値や分散などを使用せず、中央値がどれくらい離れているかで考えるため、正規分布していない場合や、外れ値がある場合でも使うことができます。
標本数nが少ない場合は母集団が正規分布かわからないので、ノンパラメトリック検定とパラメトリック検定両方使って比較する方法も有るらしいです。
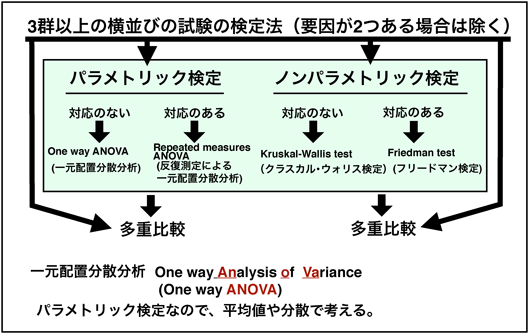
流れとしてはこのようになっています。ちなみに、ウィルコクソンの順位和検定とマンーホイットニーu検定は同じ検定結果らしいです。
順位検定についてわかってなかったので少し詳しく書きました
順位和検定は基本的にデータの並び替えで行います。両方の群のデータを小さい順に並べていって、それぞれの群の順位の中央値がどれぐらい離れているかで考えます。順位で見ているので、平均値、外れ値が関係しないわけですね。
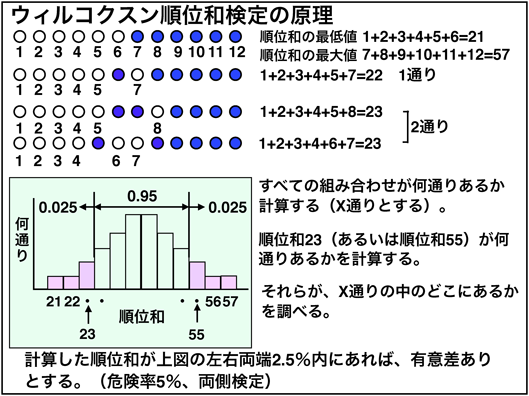
順位和検定の基本的な原理は共通しているのでここではウィルコクソンの順位和検定を例にとって説明します。
では、2つの順位の中央値がどのくらい離れていたら有意差が有ると言ったらいいのでしょうか?
pythonでの検定方法
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=10)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=10)
# Wilcoxon rank-sum test : input -> arr1,arr2
stats.ranksums(rvs1, rvs2)
# only p-value
stats.ranksums(rvs1, rvs2).pvalue
出力
RanksumsResult(statistic=0.4535573676110727, pvalue=0.6501474440948545)
0.6501474440948545
Mann-WhitneyのU検定(両側検定)
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=500)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=500)
# mann whitney u : input -> arr1,arr2
stats.mannwhitneyu(rvs1, rvs2,alternative='two-sided')
# only p-value
stats.mannwhitneyu(rvs1, rvs2, alternative='two-sided').pvalue
出力
MannwhitneyuResult(statistic=132504.0, pvalue=0.10035952816655358)
0.10035952816655358
Brunner-Munzel検定
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=10)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=10)
# Wilcoxon rank-sum test : input -> arr1,arr2
stats.brunnermunzel(rvs1, rvs2)
# only p-value
stats.brunnermunzel(rvs1, rvs2).pvalue
出力
BrunnerMunzelResult(statistic=0.8104415094807922, pvalue=0.4287646188130605)
0.4287646188130605
ウィルコクソンの符号順位検定(両側)
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=10)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=10)
# wilcoxon signed-rank test: input -> arr1,arr2
stats.wilcoxon(rvs1, rvs2)
# only p-value
stats.mannwhitneyu(rvs1, rvs2).pvalue
出力
WilcoxonResult(statistic=14.0, pvalue=0.1688069535565081)
0.04448650585090664
ノンパラメトリックのメリット、デメリット
ウィルコクソンの順位和検定で1群ごとに最低限必要なnは4、符号付き順位和検定の場合は6となり、最低限の場合はかなり厳しくなってしまうので、使い分けが必要です。
3群以上の場合
パラメトリック、ノンパラメトリックを分ける等分散性の検定としてはハートレイの検定(各群のnが同じ時)、バートレットの検定(nが違う時)などがあります。しかし、nが30前後ないと当てにならないらしく、(自分は使わなそうなので)割愛します。
pythonでの検定方法
One-way ANOVA
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=10)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=10)
rvs3 = stats.norm.rvs(loc=5, scale=30, size=10)
# One-way ANOVA : input -> arr1,arr2,arr3...
stats.f_oneway(rvs1, rvs2, rvs3)
# only p-value
stats.f_oneway(rvs1, rvs2, rvs3).pvalue
出力
F_onewayResult(statistic=0.7353489234927583, pvalue=0.48869320466576477)
0.48869320466576477
Repeated measures ANOVA
引用元:(https://www.statology.org/repeated-measures-anova-python/)
import numpy as np
import pandas as pd
# create data
df = pd.DataFrame({'patient': np.repeat([1, 2, 3, 4, 5], 4),
'drug': np.tile([1, 2, 3, 4], 5),
'response': [30, 28, 16, 34,
14, 18, 10, 22,
24, 20, 18, 30,
38, 34, 20, 44,
26, 28, 14, 30]})
from statsmodels.stats.anova import AnovaRM
# perform the repeated measures ANOVA
AnovaRM(data=df, depvar='response', subject='patient', within=['drug']).fit()
出力
Anova
==================================
F Value Num DF Den DF Pr > F
----------------------------------
drug 24.7589 3.0000 12.0000 0.0000
==================================
クラスカル・ウォリス検定
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=10)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=10)
rvs3 = stats.norm.rvs(loc=5, scale=30, size=10)
# Kruskal-Wallis H-test : input -> arr1,arr2,arr3...
stats.kruskal(rvs1, rvs2, rvs3)
# only p-value
stats.kruskal(rvs1, rvs2, rvs3).pvalue
出力
KruskalResult(statistic=2.046451612903226, pvalue=0.35943360481724507)
0.35943360481724507
フリードマン検定
from scipy import stats
rvs1 = stats.norm.rvs(loc=5, scale=10, size=10)
rvs2 = stats.norm.rvs(loc=5, scale=20, size=10)
rvs3 = stats.norm.rvs(loc=5, scale=30, size=10)
# Kruskal-Wallis H-test : input -> arr1,arr2,arr3...
stats.friedmanchisquare(rvs1, rvs2, rvs3)
# only p-value
stats.friedmanchisquare(rvs1, rvs2, rvs3).pvalue
出力
FriedmanchisquareResult(statistic=0.8000000000000114, pvalue=0.6703200460356356)
0.6703200460356356
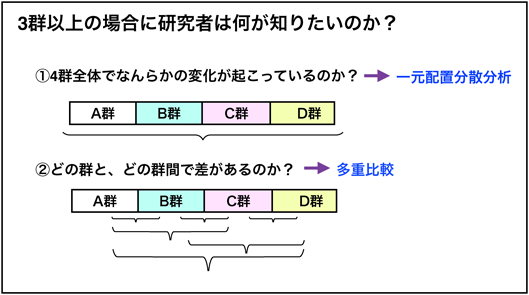
すべての群を見る検定
多群の検定では、すべての群を見る、一元配置分散分析(one-way ANOVA)などを行い、各群でどの群とどの群が有意差が有るか多重比較を行います。
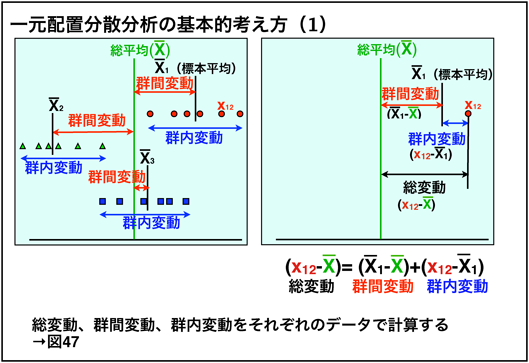
ここではすべての群を見る方法の原理として、one-way ANOVAを例にとって説明します。
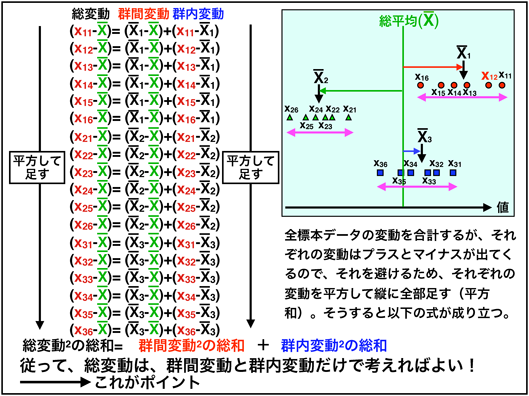
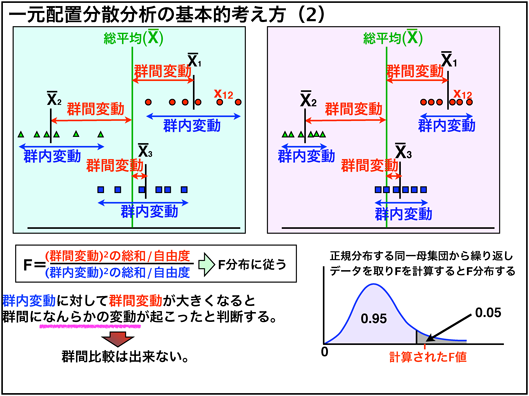
まずは、すべてのデータの平均を総平均とし、各群での平均が総平均とどれくらい離れているかを考えます。例えば図中の$X_{12}$で考えると、群の平均から離れている群内変動と総平均との離れである群間変動を足し合わせた総変動が総平均からの変動量(総変動)となります。これを各標本に対し行い、符号を無くすために平方計算します。
そうすると、図中のように、$総変動^2の総和=群間変動^2の総和+群内変動^2の総和$が成り立つため、群間変動と群内変動のみを考えれば総変動を考えることができます。
図中の左上の図を見ると、それぞれの群の間に有意差がありそうで、その場合群内変動が小さく、群間変動が大きそうです。そのため図中にあるFを計算し、Fが大きい、つまり群内変動に比べて群間変動が大きい場合に有意差がある、群内になんらかの変動がおこったといいます。
ここでは主にパラメトリック法について説明しましたが、ノンパラメトリックな時は2群の時と同様にデータを順位に置き換えて検定を行います。
なぜ多重比較なのか?
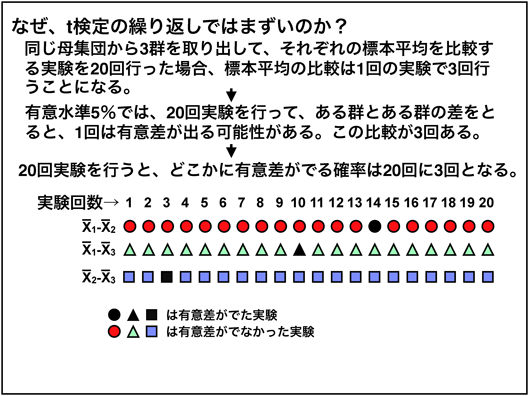
例えば、3群でt検定を行うと、有意とならない確率は(1−0.05)×(1−0.05)×(1−0.05)=0.86 となり、有意水準が5%でやっているはずなのに14%となってしまう多重性の問題が発生します。そのため、有意水準を狭め、全体の有意水準を5%に調整する多重比較が必要となります。
多重比較の検定について
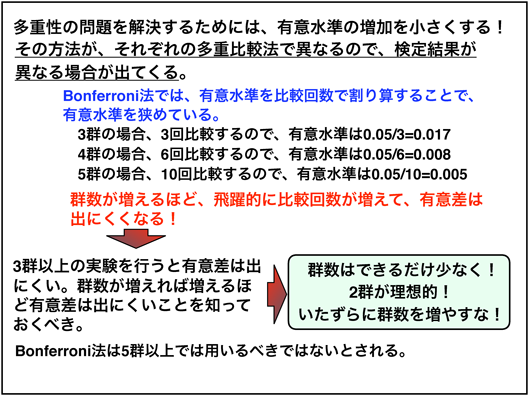
多重比較の検定方法は色々あり、例えば有意水準を群雛で割るBonferroni法などもありますが、群数が増えれば増える程、厳しくなってしまうので極力群数をへらすことが望ましいです。
多重比較を行う前の一元配置分散分析は必要か?
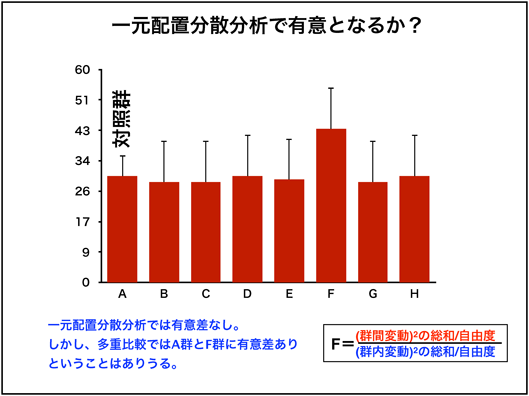
一元配置分散分析は全体で何らかの変動が行ったことを調べる方法であり、多重比較は関心のある特定の2群間での比較に注目しています。
『統計的多重比較法の基礎』では,「多重比較と通常の一元配置分散分析は別物であり,多重比較を適用するときは,その手順のなかに示されていない限りはF検定による一元配置分散分析を併用するべきではない」と述べており、多重比較の結果のみを知りたい場合は一元配置分散分析の結果はあまり考慮する必要はないと思われます。
一元配置分散分析を行う必要のない多重比較として、同書で
- Dunnet法
- Tukey–Kramer法
- Bonferroni法とその関連法
があるとされています。
また、 - Scheffe法
- Games–Howell法
- Fisher PLSD法
は一元配置分散分析のF検定で有意差がでなければ,多重比較でも差が得られない検定法とされています。
一般によく用いられる多重比較
- パラメトリック検定ー対応のない場合(等分散)
- Tukey–Kramer法、Bonferroni法とその関連法(Holm法,Shaffer法)、最小有意差法(3群のみ利用可能)
- パラメトリック検定ー対応のない場合(等分散でない)
- Games–Howell法(標本の大きさnが同じ場合に用いることができる)、ノンパラメトリック法も用いられる(Steel–Dwass法)。対照群とのみ比較する場合は,等分散の場合はDunnett法がある.等分散でない場合は,ノンパラメトリック法(Steel法)を用いる.また,たとえば,試験物質の投与量依存的にあるパラメータが次第に上昇するあるいは降下するような場合は,Williams法が有意差はでやすいとされる.
- ノンパラメトリック検定ー対応のない場合
- 全群の比較では,Steel–Dwass法があり,対照群とのみ比較する場合は,Steel法がある。Williams法のノンパラメトリック版として,Shirley–Williams法がある。母集団が正規分布しているが等分散でない場合はノンパラメトリック法を用いることができる.
- パラメトリック及びノンパラメトリック検定ー対応のある場合
- 対応のある場合の多重比較は開発されていないので,どうしても検定したい場合は,対応のない場合の検定法で代用するしかない.したがって,パラメトリック法もノンパラメトリック法も全群での比較はBonferroni法とその関連法が,対照群とのみの比較はDunnett法が用いられる.
pythonでの検定方法
Turkey-Kramer法
参考元:ObGyn.jp
import pandas as pd
from statsmodels.stats.multicomp import pairwise_tukeyhsd
data = pd.DataFrame({"デバイス": ["デバイス A", "デバイス B", "デバイス A", "デバイス A", "デバイス C", "デバイス C",
"デバイス B", "デバイス C", "デバイス A", "デバイス A", ], "出血量": [30, 20, 5, 5, 100, 80, 10, 60, 10, 25]})
pairwise_tukeyhsd(data["出血量"], data["デバイス"]).summary()
出力
Multiple Comparison of Means - Tukey HSD, FWER=0.05
======================================================
group1 group2 meandiff p-adj lower upper reject
------------------------------------------------------
デバイス A デバイス B 0.0 0.9 -34.8105 34.8105 False
デバイス A デバイス C 65.0 0.001 34.6149 95.3851 True
デバイス B デバイス C 65.0 0.0037 27.0186 102.9814 True
------------------------------------------------------
Bonferroni(Holm)
from statsmodels.stats.multitest import multipletests
import random
p_values = [random.uniform(0, 0.01) for _ in range(6)]
# method=(bonferroni,holm)
multipletests(p_values, method='bonferroni')
出力
# bonferroni
(array([ True, True, False, True, True, False]), array([0.03654118, 0.03761863, 0.05141457, 0.01703562, 0.02788418,
0.05068198]), 0.008512444610847103, 0.008333333333333333)
Steel-Dwass法
@rola_satoruさんの記事を参考にしました。
import scikit_posthocs as sp
import seaborn as sns
# タイタニックのデータをロード
df = sns.load_dataset("titanic")
# Steel-Dwass 検定
# val_colは値のカラム
# group_colは比較したい群のカラム
print(sp.posthoc_dscf(df, val_col="fare", group_col="class"))
出力
Third First Second
Third 1.000 0.001 0.001
First 0.001 1.000 0.001
Second 0.001 0.001 1.000
Dunnett法
参考元:scikit_posthocs 公式ドキュメント
import scikit_posthocs as sp
import numpy as np
x = [[1, 2, 3, 5, 1], [12, 31, 54, np.nan], [10, 12, 6, 74, 11]]
# 公式ではmethod='holm'を追加していましたが、正直なぜ入れてたのはわからないです
sp.posthoc_dunn(x)
出力
1 2 3
1 1.000000 0.010178 0.030839
2 0.010178 1.000000 0.484029
3 0.030839 0.484029 1.000000
Steel法?(自動選択してくれる?)
参考元:scikit_posthocs 公式ドキュメント
import scikit_posthocs as sp
import pandas as pd
x = pd.DataFrame({"a": [1,2,3,5,1], "b": [12,31,54,62,12], "c": [10,12,6,74,11]})
x = x.melt(var_name='groups', value_name='values')
sp.posthoc_dscf(x, val_col='values', group_col='groups')
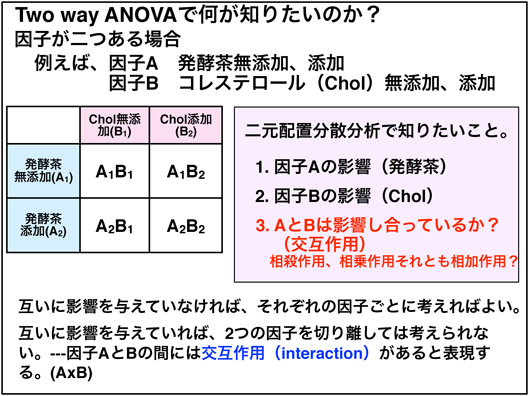
二元配置分散分析
2元配置分散分析では、試験したい因子が2つ有り、それら2つの因子がそれぞれ独立して影響を当たるのか、相互に影響しあっているのかを知りたい時に用いられる。
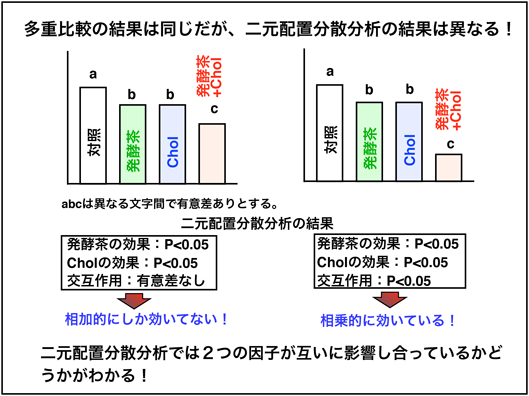
例えば上図では、左の図はそれぞれでの効果はあるが、それが相互作用を及ぼしていない(相加的にしか効いていない)こと、右の図では相互作用を及ぼしている(相乗的)ことがわかります。
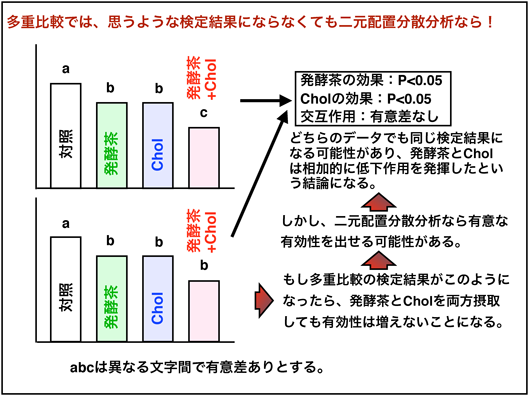
例えば上図のように、それぞれの場合では有意差があっても、片方のみ入れた場合とそれを2つとも入れた場合で有意差がみられないという場合に相乗的ということが示せればこの2つを組み合わせることが効果的であるということが言えます。
pythonでの分析
import statsmodels.api as sm
from statsmodels.formula.api import ols
moore = sm.datasets.get_rdataset("Moore", "carData", cache=True) # load
data = moore.data
data = data.rename(columns={"partner.status":
"partner_status"}) # make name pythonic
moore_lm = ols('conformity ~ C(fcategory, Sum)*C(partner_status, Sum)',
data=data).fit()
table = sm.stats.anova_lm(moore_lm, typ=2) # Type 2 Anova DataFrame
出力
sum_sq df F PR(>F)
C(fcategory, Sum) 11.614700 2.0 0.276958 0.759564
C(partner_status, Sum) 212.213778 1.0 10.120692 0.002874
C(fcategory, Sum):C(partner_status, Sum) 175.488928 2.0 4.184623 0.022572
Residual 817.763961 39.0 NaN NaN
二元配置分散分析の解釈の仕方
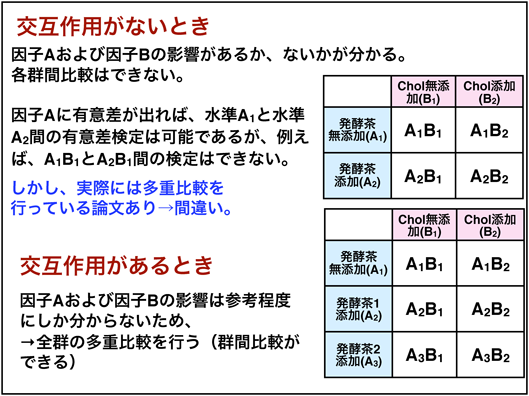
2×2の二元配置分散分析では、交互作用に有意差がない場合、それ以上の検定を行う必要はなく、多重比較よりもこの分析結果を優先して論じるべきです。
有意差が見られた場合は、それぞれの因子が互いに影響しあっていることになるので、すべての群を独立した群と考えて多重比較を行います。つまり、交互作用がある場合は多重比較による群間比較が可能となります。
おわりに
色々抜けとか、プログラムが見つからないところがあり、完璧とは言えないですが、最後まで書け(要約でき)て、達成感を味わえました。
アドバイスなどがあればコメントなどをくださると喜びます。
この記事を執筆していく中で、自分なりに統計検定に関する知識が深まっていく気がしたので目的達成ということでよかったです。