忙しい人のために
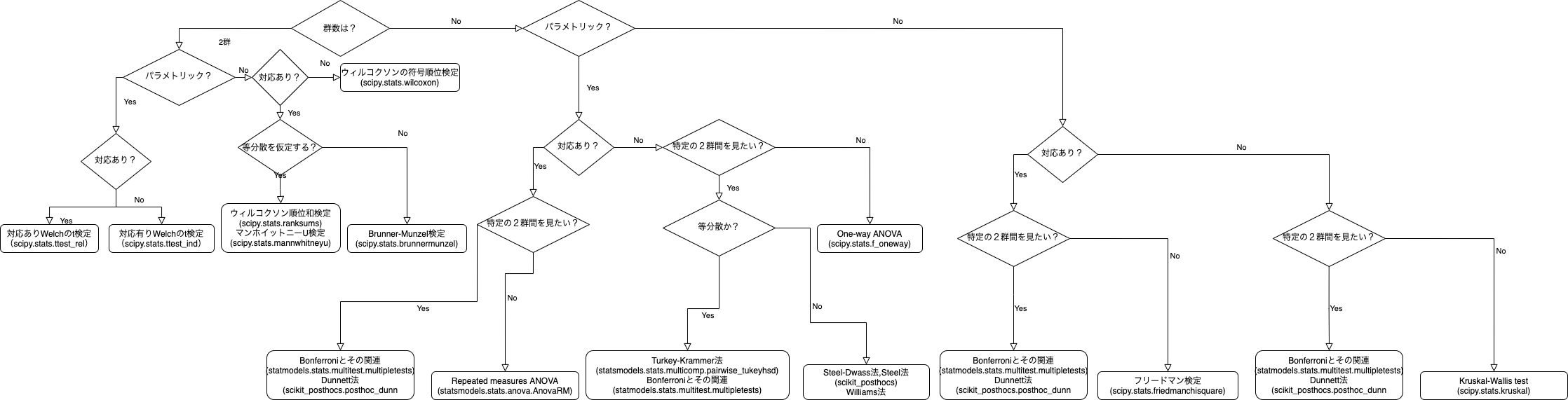
このフローチャート(的なもの)をみれば選択できるように作りました。
文字サイズが小さいので、別ページで開くなりして下さると楽に見れると思います。
(個人的な記事を書いた動機なので)TL; DR;
自分は、現在B4の情報系大学生です。この前卒論があったのですが、統計の検定のやり方があまりわかっておらず先輩のやったものを見様見真似でやっていたら提出直前に大変でした。そのため、このようなことを2度としたくないという自戒が一番なのですが、この記事でこのようなミスをする人が減ったらいいなと思ったのもあり、今回これを見ればさわりはわかって使い分け用途を理解して使えることを目的として、執筆する形となりました。
参考文献
以下のページを基本的には要約(改悪)した形となっています。
こんな本、記事もあるよ!という方はコメントで教えてくださるとありがたいです。
改定増強版:統計検定を理解せずに使っている人のために Ⅰ
改定増強版:統計検定を理解せずに使っている人のために Ⅱ
[改定増強版:統計検定を理解せずに使っている人のために Ⅲ]
(https://katosei.jsbba.or.jp/view_html.php?aid=1208)
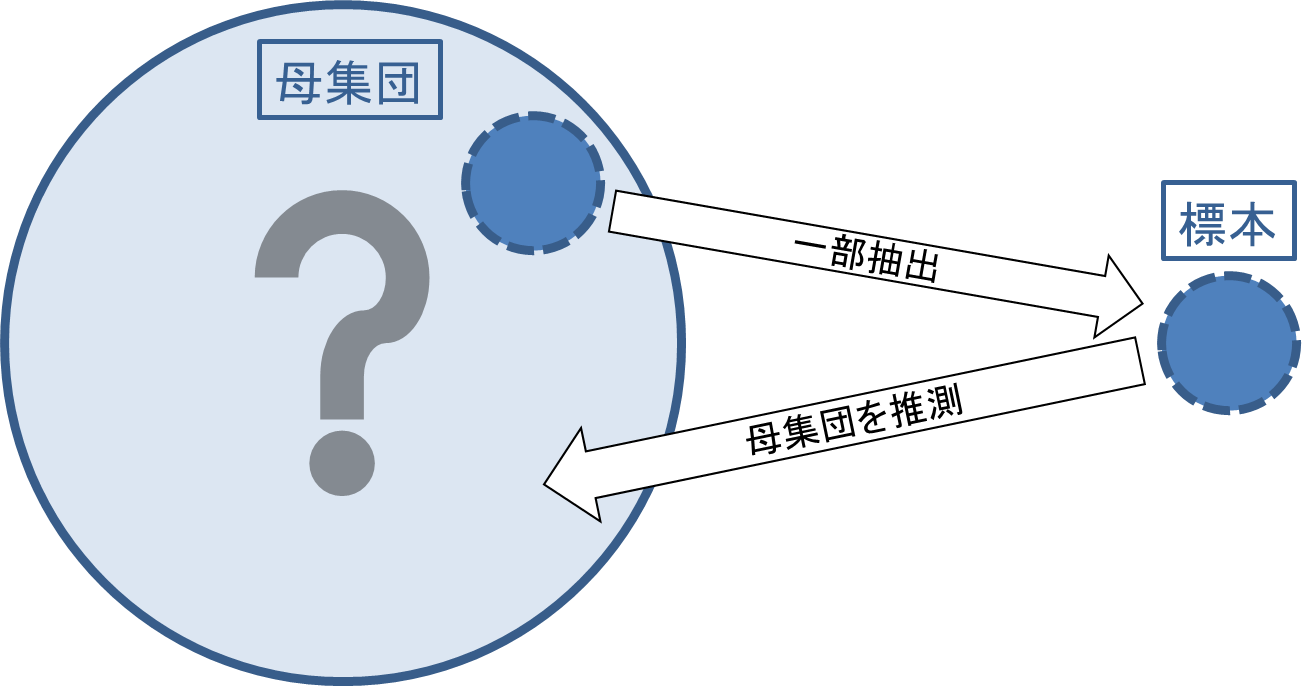
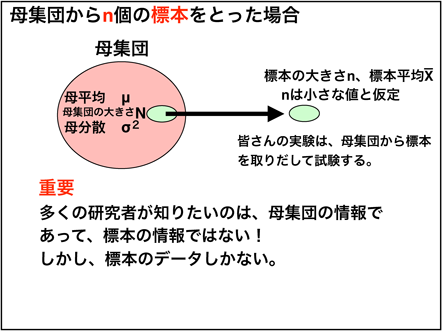
自分たちが見ているデータは?
自分たちは母集団から標本を抽出し、実験を行います。
(例:○人にアンケートなど)
引用元:統計WEB 母集団と標本
では、その標本のデータを使って知りたいのは、何に関する情報なのでしょうか?
○人にアンケートを取って、その人達は✗✗の傾向がある、ほかは知らん!とかやっても、世界に役立つのが研究なので、あまり意味がないと考えられます。
その標本から取ったデータが全体に当てはまる、つまり、母集団に関しても同じことを言えれば普遍的に言える事柄と言えれば、世の中への貢献度が上がります。そのため、常に母集団が何かということを考え、データを見る必要があります。
って言ってもどうやってデータを見ればいいんですか??
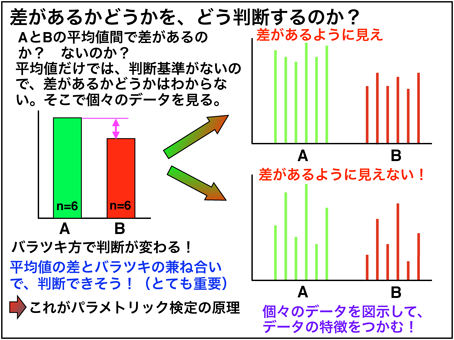
この図でのA、Bの群間で差があるかわかりますか?
まぁ、目で見て一律の基準で人間が判断できれば検定なんていりません。
差を見る時は時は被験者全体と各被験者ごとに分けてデータを見るのが重要です(1敗)。
全体の平均では差がありそうに見えますが(図の左)、各被験者において図の右上の場合と右下の場合で見ると右下は個人差が大きく本当に差があるかはわからなくなってきます。このように全体での平均と、各被験者でのばらつきをみるのがパラメトリック検定の原理となっています。
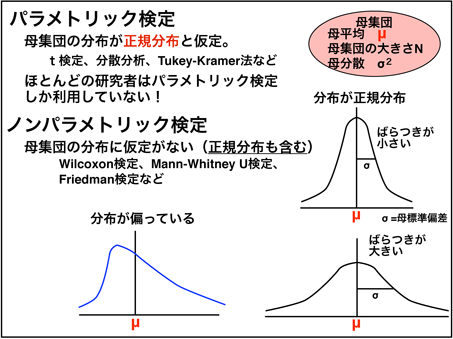
いや、パラメトリック検定って何やねん
パラメトリック検定とは、標本から採取する時の基の母集団の分布が正規分布に従っていると仮定した場合の検定方法となります。分布を仮定しない場合はノンパラメトリック検定という方法を用います。
じゃあなんで、パラメトリックが存在してるんだ、という話なんですが、母集団を仮定したほうが標本から母集団を推定しやすく、だいたい世の中のものは正規分布に従っているからです。しかし、正規分布していないときにパラメトリック検定を用いてもあまり意味がなく大変なことになってしまいます(1敗)。意味がない理由については後述します。
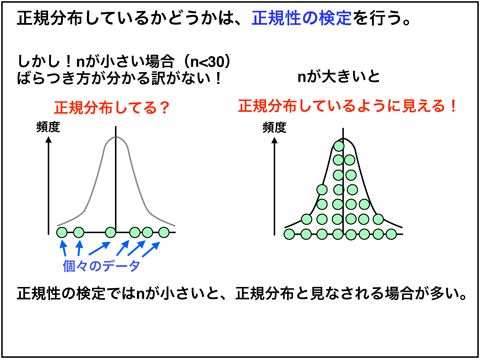
では、母集団の分布が正規分布かどうかを知る方法に関してですが正規性の検定を行えば知ることができます。正規性の検定に関しては後で追加します。
しかし、nが小さい(n<12とある統計ソフトでは定義されている)と正規分布と誤認される場合が多く、正規性検定は行なえません。その場合は、これらのことを踏まえた上でパラメトリック検定を行うのが一般的らしいです。
平均値に関しては完全に理解した、分布のばらつきの見方は??
分布のばらつきの見方は
- 数値のばらつき方を示す指標としての分散
- データのありそうな範囲の指標として標準偏差
が存在し、これらの値を参考にする必要があります。
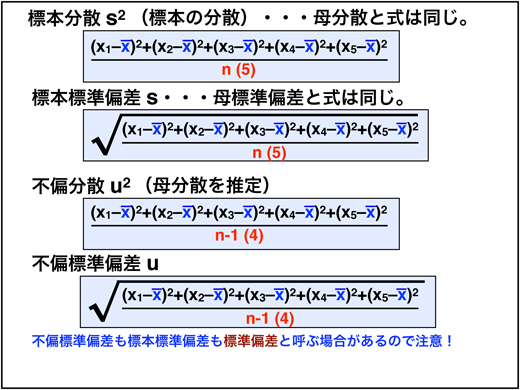
しかし、実験によって得られたのは標本に関するデータのみで、これから母集団の分散、標準偏差を求めなければいけません。そのためには、不偏分散、不偏標準偏差という標本の分散、標準偏差を母集団の分散、標準偏差に等しくなるように補正した値を用います。
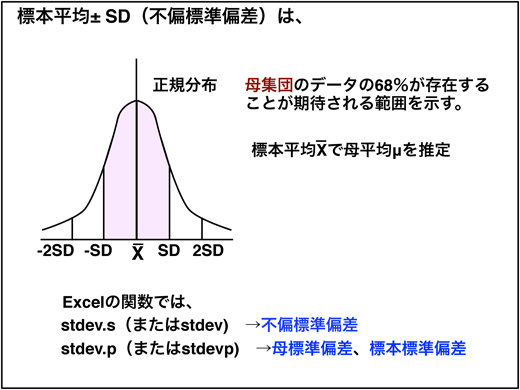
標本平均±不偏標準偏差は、母集団のデータの68%が存在することが期待される範囲です。標本平均±2*不偏標準偏差は96%を表しています。
標本平均±不偏標準偏差は母平均と、母集団のばらつきをしめしています。
しかし、母集団のばらつきに興味がない場合は標準誤差というものを用いたほうがいいです。
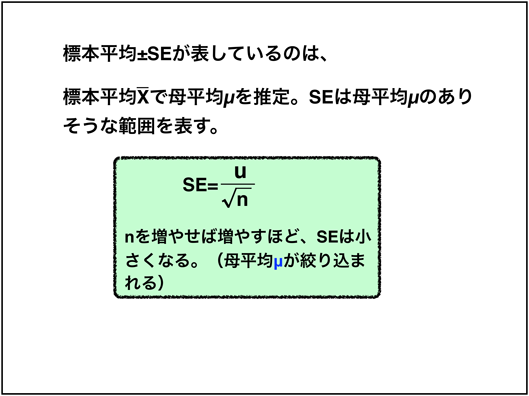
標準誤差とは?
標準誤差とは母平均がありそうな範囲を示しています。標準誤差は標本数nが大きくなるほど、小さくなる性質が存在します。
標準偏差と標本誤差の使い分け方
この2つは以下の基準で使い分けを行います。
- 標準偏差
- 母平均と母標準偏差両方、つまりデータがどの程度ばらついているかを知りたい時
- 標準誤差
- 母平均のみ、つまり母平均がどこらへんにあるかを知りたい時
それでは次は具体的な検定方法について、執筆をしていきたいと思います。
次の記事:https://qiita.com/students/items/a6838a769b706a801a03