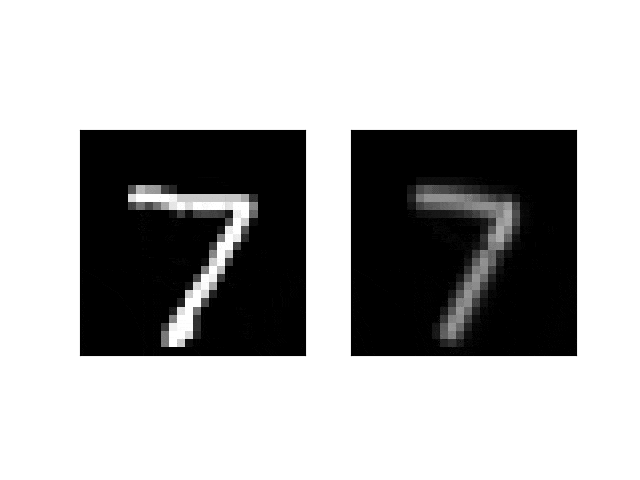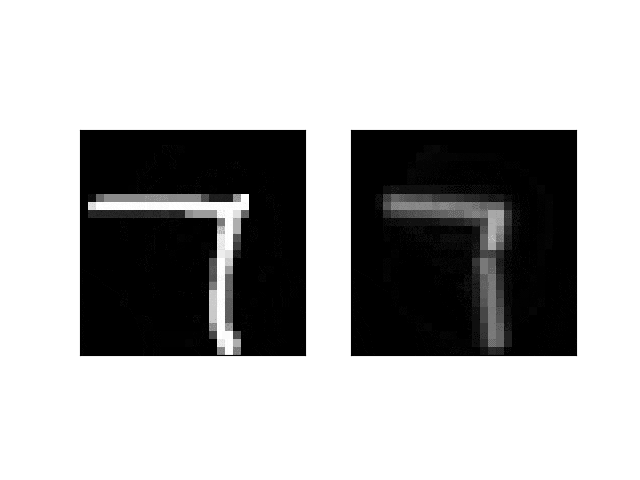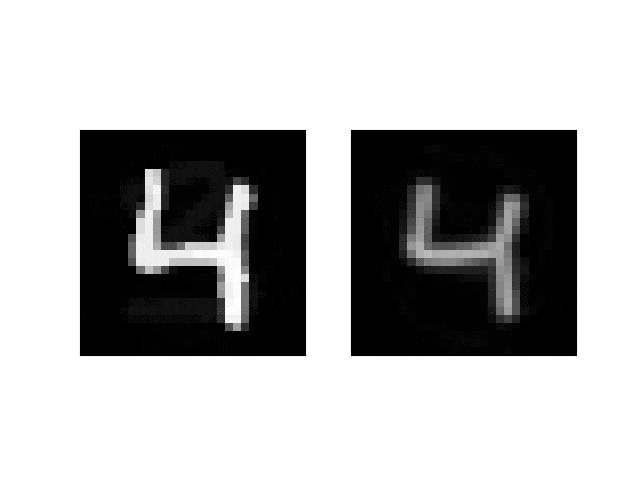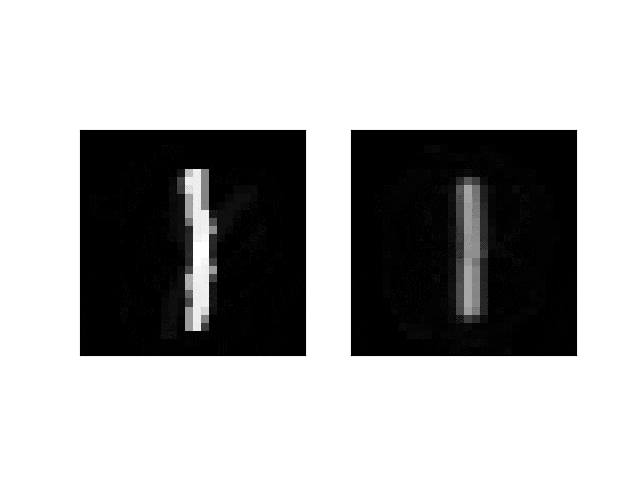はじめに

以前MNISTの筆跡推定をやってみたのですが、すこし別のアプローチを考えてみました。
前回はLSTM＋シンプルな描画系を使いましたが、今回はMLP+ベジェ曲線描画系を使ってみます。

実装

全体の構成は下記のようになっています:

(入力画像) -> MLP -> (制御点列) -> 描画系 -> (出力画像)

描画系ではベジェ曲線の制御点列を入力、画像を出力とします。
ベジェ曲線の描画アルゴリズムは調べたらすぐ出てきますので、概ね素直に移植すればOKですが、下記の点少し工夫しています。

接線が折れ線にならないようにするため、角度・前方向長さ・後方向長さで定義します
ストロークは複数本に分けずに、1本の線の色の濃さを変えながら描画します(変数touchがこれにあたります）

実験用コードです：


import os,sys
import numpy as np
import keras
from keras.datasets import mnist
from keras.models import Model, Input 
from keras.layers import Reshape, Dense, Lambda, Flatten
from keras import backend as K 

batch_size = 128
epochs = int(sys.argv[1]) # set 0 to display sequence
points = 8
display_size = 28
interpolation = 20 # 学習時:10
sigma = 0.05 # 学習時:0.1

weights_enc = "weights_enc.hdf5"
train = True if epochs>0 else False

def MLPModel(num_points,hidden_units=128,input_shape=(28,28,1)):
    x = Input(shape=input_shape)
    h = Flatten()(x)
    h = Dense(hidden_units,activation="relu")(h)
    h = Dense(hidden_units,activation="relu")(h)
    h = Dense(num_points*6)(h) # x,y,theta,mag0,mag1,touch
    y = Reshape((num_points,6))(h)
    return Model(inputs=[x],outputs=[y])

def BazierImageLayer(num_points,interpolation=10,size=28,sigma=0.1,closed=False):
    def draw(x):
        z = K.zeros_like(x)[:,0,0]
        image = K.reshape(K.stack([z]*size*size),(-1,size,size)) 

        base = x[:,:,0:2]
        dx = K.cos(x[:,:,2])
        dy = K.sin(x[:,:,2])
        direction = K.stack((dx,dy),-1)
        mag_forward = K.maximum(x[:,:,3,None],0.0)
        mag_backward = K.maximum(x[:,:,4,None],0.0)
        touch = K.sigmoid(x[:,:,5,None,None])

        coord = K.constant(np.arange(size).reshape(1,size)/size-0.5)

        num_draw = num_points if closed else num_points-1
        for i in range(num_draw):
            j = (i+1)%num_points
            p0 = base[:,i]
            p1 = base[:,i] + direction[:,i]*mag_forward[:,i]
            p2 = base[:,j] - direction[:,j]*mag_backward[:,j]
            p3 = base[:,j]
            for t in range(interpolation):
                r = t/interpolation
                xy  = p0 * 1        * (1-r)**3
                xy += p1 * 3 * r**1 * (1-r)**2
                xy += p2 * 3 * r**2 * (1-r)**1
                xy += p3 * 1 * r**3

                # pen profile
                g = (1/sigma)**2
                px = K.exp( -K.pow(coord-xy[:,0:1],2)*g)
                py = K.exp( -K.pow(coord-xy[:,1:2],2)*g)
                px = K.reshape(px,(-1,1,size))
                py = K.reshape(py,(-1,size,1))

                # draw
                image = K.maximum(image,touch[:,i]*px*py)

        image = K.minimum(image, 1.0)
        return K.expand_dims(image)
    return Lambda(draw)

if __name__ == "__main__":
    # the data, shuffled and split between train and test sets
    (x_train, y_train), (x_test, y_test) = mnist.load_data()
    x_train = x_train.reshape(60000, 28,28,1)
    x_test = x_test.reshape(10000, 28,28,1)
    x_train = x_train.astype('float32')
    x_test = x_test.astype('float32')
    x_train /= 255
    x_test /= 255
    print(x_train.shape[0], 'train samples')
    print(x_test.shape[0], 'test samples')

    ## encode model
    model_enc = MLPModel(points)
    ## main model
    x = Input(shape=(28,28,1))
    x_enc = model_enc(x)
    x_image = BazierImageLayer(points,interpolation=interpolation,size=display_size,sigma=sigma)(x_enc)
    model = Model(inputs=[x],outputs=[x_image])
    model.summary()

    if os.path.exists(weights_enc):
        model_enc.load_weights(weights_enc)

    if train:
        model.compile(loss='mse',optimizer=keras.optimizers.Nadam())
        history = model.fit(x_train, x_train,
                            batch_size=batch_size,
                            epochs=epochs,
                            verbose=1,
                            validation_data=(x_test, x_test))
        model_enc.save_weights(weights_enc)

    ## export to png file with matplotlib
    import matplotlib.pyplot as plt
    n = 8
    img0 = x_test[:n**2]
    img1 = model.predict(img0.reshape((-1,28,28,1)))

    plt.figure(num=None, figsize=(8, 6), dpi=160) 
    for i in range(n**2):
        plt.subplot(n,n,i+1)
        plt.tick_params(labelbottom="off",bottom="off",labelleft="off",left="off")
        plt.imshow(img0[i,:,:,0], 'gray', vmin=0, vmax=1)
    plt.savefig("target.png")

    plt.figure(num=None, figsize=(8, 6), dpi=160) 
    for i in range(n**2):
        plt.subplot(n,n,i+1)
        plt.tick_params(labelbottom="off",bottom="off",labelleft="off",left="off")
        plt.imshow(img1[i,:,:,0], 'gray', vmin=0, vmax=1)
    plt.savefig("predict.png")
    exit()

    ## interpolation experiment
    import cv2
    import matplotlib.pyplot as plt
    import numpy as np

    x_target = x_test # x_test[y_test==4]
    a = 0
    for i in range(100):
        b = a
        a = np.random.randint(1000)
        for t in range(15):
            r = t/15
            img0 = r*x_target[a] + (1-r)*x_target[b]
            img1 = model.predict(img0.reshape((1,28,28,1)))[0]

            # disp        
            cv2.imshow("gt",img0)
            cv2.imshow("predict",img1)
            k = cv2.waitKey(60)

            # # write to file
            # # generate gif animation : convert -layers optimize -loop 0 -delay 15 interpolation*.png interpolation.gif
            # frame = i*15+t

            # plt.subplot(1,2,1)
            # plt.tick_params(labelbottom="off",bottom="off",labelleft="off",left="off")
            # plt.imshow(img0[:,:,0], 'gray', vmin=0, vmax=1)
            # plt.subplot(1,2,2)
            # plt.tick_params(labelbottom="off",bottom="off",labelleft="off",left="off")
            # plt.imshow(img1[:,:,0], 'gray', vmin=0, vmax=1)
            # plt.savefig("interpolation{:0>3}.png".format(frame))

        k = cv2.waitKey(0)
        if k==27:
            break