LSTMでMNISTの筆跡を推定する

はじめに

GANやVAEといった生成系モデルが目覚ましい進展を見せています。これらのモデルにおいて、生成過程はCNNやRNNといった比較的汎用性の高い方法を使っています。しかし、生成過程になんらかの前提知識がある場合は、それを使わないのはもったいない感じもします。
そこで今回の投稿では、生成過程や観測過程の知識をニューラルネットワークに組入れるアプローチをやってみます。いわばペン描画シミュレーター+ニューラルネットワークのEnd2End学習というところでしょうか。このようなアプローチが充実してくれば、CAEやロボティクスなど、シミュレーションや制御に関する知見が豊富なところでの応用がしやすくなることも期待されます。
先行研究がありそうですが、実際に手を動かしたい気分だったので勢いでやりました。趣味の研究なのでいいことにします。
先行研究についてご存知の方がいましたら、教えていただけるとありがたいです。

ちなみに、一瞬ディープラーニングのタグをつけようかと思いましたが、特にディープ要素はないですね。

コードはこちらにあります：
https://github.com/stnk20/mnist_draw

2018-03-03追記：
やはり先行研究がありました。
"DRAW: A Recurrent Neural Network For Image Generation"
https://arxiv.org/abs/1502.04623
エンコード側の構成がだいぶ違いますが、デコード側（出力側）はより汎用的な構成になっています。

2018-03-15追記：
隠れ層での補間を試してみました。

方法

出力系

まずは、出力系の構成について見ていきます。
ゲームエンジン等で描画過程およびダイナミクスを構成するのが楽ですが、出力系が微分できなくなってしまいますので、典型的には強化学習と組み合わせます。こういう手法は事例も豊富にあるのですが、強化学習は学習収束に時間がかかりそうで、できれば避けたいです。
少し立ち返って、文字を書くというタスクをよくよく考えてみると、実は微分可能な形で構成できることがわかります。ということで、Kerasのバックエンドを使って微分可能な出力系をつくってみました。

class DrawImageLayer(Layer):
    def __init__(self, size=28, return_sequences=False, **kwargs):
        self.size = size
        self.return_sequences = return_sequences
        self.range = K.constant(np.arange(size).reshape(1,size)/size-0.5)

        super(DrawImageLayer, self).__init__(**kwargs)

    def build(self, input_shape):        
        super(DrawImageLayer, self).build(input_shape) 

    def call(self, x):
        initial_states = self.get_initial_states(x)
        last_output, outputs, states = K.rnn(self.step, x, initial_states)
        if self.return_sequences:
            return outputs
        else:
            return last_output

    def compute_output_shape(self, input_shape):
        return (input_shape[0],self.size,self.size,1)

    def step(self, inputs, states):
        ## input: channels=3. x/vx,y/vy,touch
        ## states: len=3. x,y,image

        # dynamics
        x = K.reshape(inputs[:,0],(-1,1))
        y = K.reshape(inputs[:,1],(-1,1))

        # dynamics (velocity input)
        # dt = 1
        # x = states[0]+dt*K.reshape(inputs[:,0],(-1,1))
        # y = states[1]+dt*K.reshape(inputs[:,1],(-1,1))

        # pen profile
        sigma = 2/self.size
        g = (1/sigma)**2
        px = K.exp( -K.pow(self.range-x,2)*g)
        py = K.exp( -K.pow(self.range-y,2)*g)
        px = K.reshape(px,(-1,1,self.size))
        py = K.reshape(py,(-1,self.size,1))

        # draw
        image = K.maximum( states[2], K.reshape(inputs[:,2],(-1,1,1))*px*py )
        image = K.minimum( image, 1.0)

        new_states = [ x,y,image ]
        return K.expand_dims(image), new_states

    def get_initial_states(self,inputs):
        # build an all-zero tensor of shape (samples,)
        z = K.zeros_like(inputs)  # (samples, timesteps, input_dim)
        z = K.sum(z, axis=(1, 2))  # (samples,)

        ## dynamics 
        d = K.reshape(z,(-1,1))

        ## image
        z1 = K.expand_dims(z)
        image = K.reshape(K.stack([z]*self.size*self.size),(-1,self.size,self.size)) 

        return [d,d,image]

以下、要点を少し解説します。

ペンの移動ダイナミクス

速度を入力とする方式やノイズを付加するなど、派生系は色々考えられますが、一番シンプルな位置を入力する方式としています。

x = K.reshape(inputs[:,0],(-1,1))
y = K.reshape(inputs[:,1],(-1,1))

描画系

描画系ではペンの位置と記入有無を受け取り、その位置に点を描画して画像を出力します。ペン形状をガウシアンとすれば、回転対称かつxy座標を分離した形で表現できます。裾がある程度長いほうが勾配法での学習に有利な気がしますが、やりすぎると出力画像がボケてしまいます。

# pen profile
sigma = 2/self.size
g = (1/sigma)**2
px = K.exp( -K.pow(self.range-x,2)*g)
py = K.exp( -K.pow(self.range-y,2)*g)
px = K.reshape(px,(-1,1,self.size))
py = K.reshape(py,(-1,self.size,1))

# draw
eps = 0.1
image = K.maximum( states[2], K.reshape(inputs[:,2],(-1,1,1))*px*py )

その他ポイント

ここが結構大事で、画像全体を表すスケールを -0.5 < x < 0.5 に正規化しています。これをしないと学習初期に点の移動量が小さすぎて、学習が進みません。

self.range = K.constant(np.arange(size).reshape(1,size)/self.size-0.5)

エンコーダー・デコーダー

エンコーダーでは簡単な次元圧縮をしておきます。あとで特徴量の可視化に使います。

def LinearEncodeModel(filters=32,input_shape=(28,28,1),trainable=True):
    x = Input(shape=input_shape)
    h = Flatten()(x)
    y = Dense(filters,trainable=trainable)(h)
    return Model(inputs=[x],outputs=[y])

デコーダーはLSTMベースです。といっても用意されたモジュールを使うだけですね。
出力系に入力するために 時刻ステップ数S x コマンド3種類 の形状にデコードします。各時刻ごとに独立して処理するためにカーネルサイズを1としたConv1Dを使います。Timedistribute+Denseを使っても同じです。

def LSTMDecodeModel(steps,units=32,input_size=32,trainable=True):
    x = Input(shape=(input_size,))
    h = RepeatVector(steps)(x)
    h = LSTM(units,return_sequences=True,unroll=True,trainable=trainable,implementation=2)(h)
    y = Conv1D(3,1,trainable=trainable)(h)
    return Model(inputs=[x],outputs=[y])

学習

今回はラベルデータは使わず、描画結果と元画像の平均２乗誤差を最小化するように学習します。

結果1 出力

20エポック回したあとの結果を紹介します。
検証用の目標出力はこちらです。学習用データには含まれていないデータです。

出力シーケンスをアニメーションにしてみました。
シンプルなモデルながら、予想以上に良い結果が得られています。

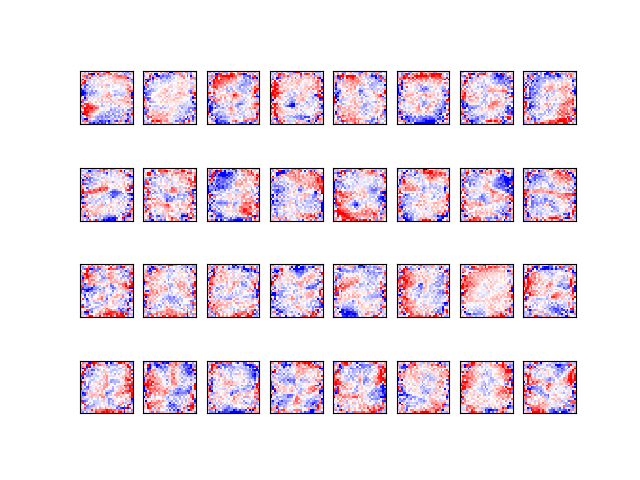
結果2 次元圧縮の可視化

エンコーダー層を可視化してみます。

結果3 隠れ層での補間

隠れ層で補間をすることで、意味的に補間をできることが期待できますので、やってみます。
なお今回はエンコーダーが線形なので、画像をそのまま線形補間すれば望む出力が得られます。

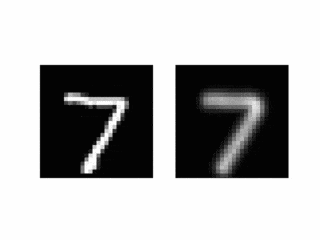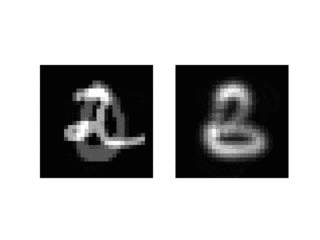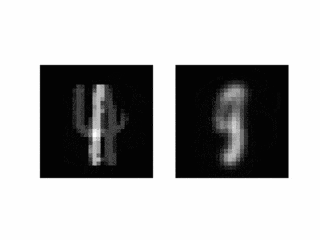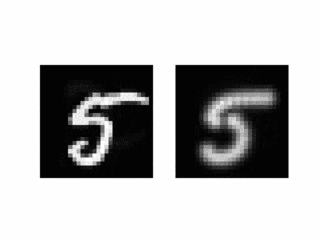
考察

• 通常1画で書くところを複数に分けて書いたりしています。まあ書き順は教えていないので仕方ないですね。とめ・はね等のダイナミクスやノイズ項を出力系に組み込むとか、適当なところにスパース性を入れると1画で書く指向が強くなりそうです。
• 別の字であっても似たような軌道で書いているケースが多いようにみえます。LSTMといっても、隠れ変数が32次元の1段だけと、表現力に限りのあるネットワークなので、できるだけ覚えることの少ない方法をとったということでしょうか。もっと表現力の高いモデルを使うとどうなる気になります。
• 次元圧縮の結果はちょっと解釈しがたいんですが、なんとなくペンの上げ下げタイミングやカーブの曲がり具合に対応した変数などがありそうな感じがします。LSTMの内部状態も含めて丁寧に可視化すれば、理解しやすくなるかもしれません。
• デコーダーは（速度ではなく）直接位置を出力していますが、なめらかな軌道になっています。デコーダーの構成要素は非線形とはいえ連続な関数であることが原因と考えられます。多段LSTMなど表現力がもっと高いもでるを使うと、この性質は弱くなると予想されます。

おわりに

LSTMすごいですね。たった32変数の隠れ変数ながら、きちんと文字が書けています！
最近、色々な要素機能を微分可能に表現して、それらモジュールをつなげて機能を作っていく、というトレンドがありますが、今回のようにシミュレーターを組み込むことで、その可能性が広がるのではないでしょうか。今回の投稿をきっかけに、他のタスクに挑戦する人が続いてくれると嬉しいです。

周辺の課題もいろいろ考えることができますが、また気が向いたらやってみることにします。

• ラベルデータも入力として使う
• 表現力の高いデコーダーを使ってみる
• ダイナミクスをよりリアルに再現する
• 弱教師あり学習や1-shot学習のための特徴抽出として使う
• 別のデータセットに適用する