ずいぶんニッチな内容になってしまいますが、案外似たような内容がなかったのでメモしておきます。
階層的クラスタリングとは
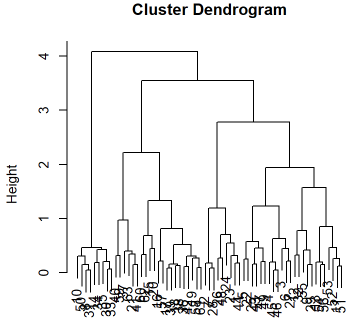
詳しい内容は他記事に任せますが…、図のようにデータ同士の近さを可視化してどのあたりに似たデータが固まっているかを確認する手法です。
ただし、神嶌先生の解説ページに
クラスタリングは探索的 (exploratory) なデータ解析手法であって,分割は必ず何らかの主観や視点に基づいているということです.よって,クラスタリングした結果は,データの要約などの知見を得るために用い,客観的な証拠として用いてはなりません.
とあるように、どのような主観や視点でデータを分割しているのかを正しく理解して知見化していくことが大切です。
手法選択について
特に注意すべきパラメータとして距離の定義と併合方法があります。
距離はデータ同士の差をどう定義するか、併合方法はクラスタとクラスタの近さをどう定義するか、ということになります。
距離の定義
仮にこんな身長体重のデータがあったとして
| 名前 | 身長[cm] | 体重[kg] |
|---|---|---|
| A | 160 | 50 |
| B | 170 | 50 |
| C | 160 | 55 |
| D | 165 | 55 |
Aさんを基準にみたとして、B,C,Dさんとどれくらい似てるかを数値化するのが距離の定義です。身長が10cm違うだけ(B)、体重が5kg違うだけ(C)、身長体重が5cm,5kg違う(D)さん。これをいつもの様々な距離定義で計算を行うと
| 距離 | ユークリッド | マンハッタン | チェビシェフ |
|---|---|---|---|
| AとB | 10 | 10 | 10 |
| AとC | 5 | 5 | 5 |
| AとD | 7.07 | 10 | 5 |
という具合に異なる答えとなります。
結局これも正解があるわけでなく、体重が異なる・身長が異なる・両方が異なるという事象をどう評価するか次第です。
あと、身長と体重のような相関が強いであろうデータを扱いやすいマハラノビス距離というのもあります。
併合方法
もう一つ、クラスタ同士の併合方法もいくつか種類があります。
Albertさんの記事の図が分かりやすいですが、クラスタ同士の近さを表すにもいくつも方式があり、最も近い点同士を距離とする方法(最短距離法)や全ての組み合わせを見る方法(群平均法)などがあります。
今回はこちらの併合方法の違いでクラスタがどう変わるかを見てみるという趣旨です。
Rによる階層的クラスタリング
R言語で階層的クラスタリングを行ってみます。
距離の計算と併合をそれぞれ行うのですが、それぞれの関数でmethodという引数を指定でき、ここで方法を指定します。
# データ読み込み
data <- read.csv("data.csv",header = T)
# 距離の計算
ret.dist <- dist(data, method = "euclidean")
# 併合してデンドログラムを作成
ret.hclust <- hclust(ret.dist, method = "complete")
# デンドログラムをもとに指定個数にクラスタを分ける
cluster <- cutree(ret.hclust,k=5)
- 距離の指定
- "euclidean" …ユークリッド距離 (デフォルト)
- "manhattan" …マンハッタン距離
- "canberra" …キャンベラ距離 など
- 併合方法
- "complete" …最長距離法(デフォルト)
- "single" …最短距離法
- "average" …群平均法
- "ward.D2" …ウォード法 など
比較してみる
距離は親しみやすいユークリッド距離にして、併合方法を4つ試してみます。
こんな2次元データをクラスタリングしてみます。
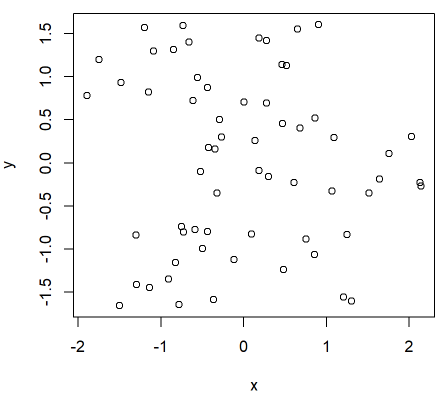
このデータから15⇒10⇒5個のクラスタを生成してみて、どのようにクラスタが併合されるか確認します。
デンドログラムと15,10,5分割した結果を表示する関数はこんな感じで作りました。
hclustree <- function(data, dist.method = "euclidean", hclust.method = "complete", k = 5){
ret.dist <- dist(data, method = dist.method)
ret.hclust <- hclust(ret.dist, method = hclust.method)
par(mfrow=c(2,2))
plot(ret.hclust)
for(kk in (k * c(3,2,1))){
col.palette <- rainbow(kk)
cluster <- cutree(ret.hclust,k=kk)
plot(data, col = col.palette[cluster])
text(data,labels = cluster)
}
}
最短距離法
hclustree(d, dist.method = "euclidean", hclust.method = "single")
(赤枠は後で付け足したものです。)
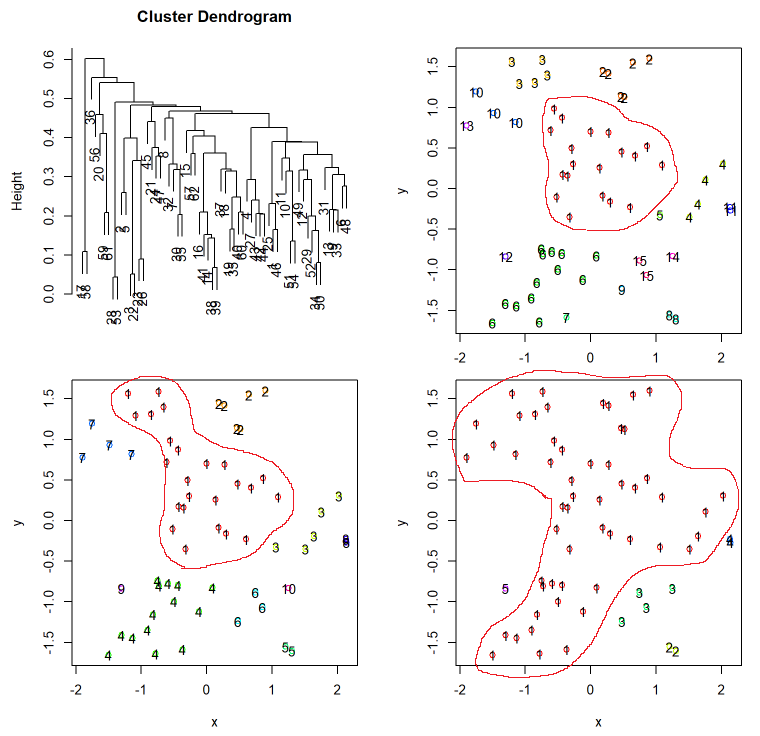
最短距離法では近くのクラスタを吸収していくようなイメージになります。そのためデータの分布によってはこのようには一つのクラスタにどんどん吸収されていく「鎖効果」が起こります。
最長距離法
hclustree(d, dist.method = "euclidean", hclust.method = "complete")
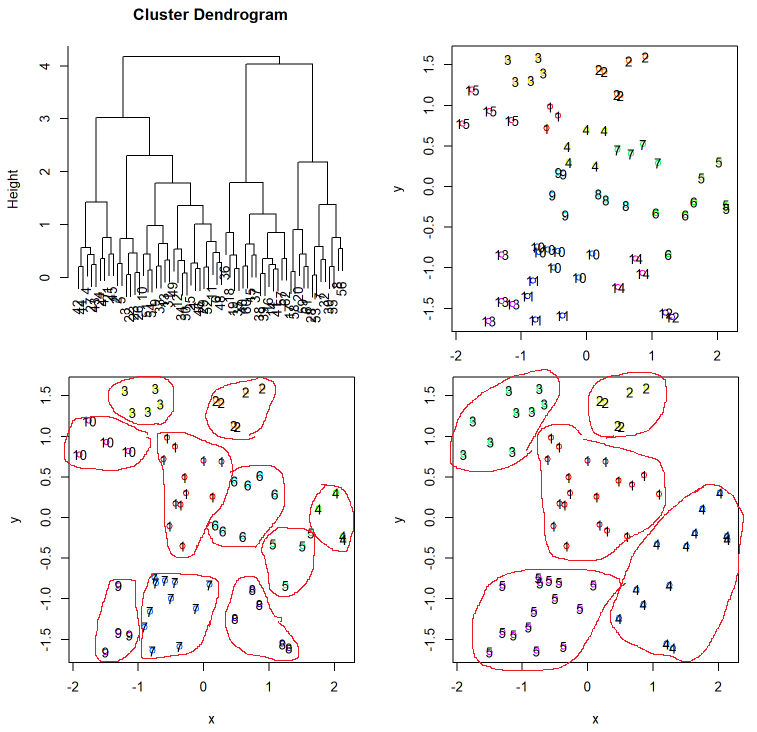
最長距離法では鎖効果は起きにくくなっていますが、逆に(今回の例では出ていませんが)新たにできたクラスタがほかのクラスタを併合しにくくなるという性質があります。円状のクラスタができやすかったりもします。
ウォード法と群平均法
hclustree(d, dist.method = "euclidean", hclust.method = "average")
hclustree(d, dist.method = "euclidean", hclust.method = "ward.D2")
群平均法とウォード法では大体似たような傾向になりました。
群平均法
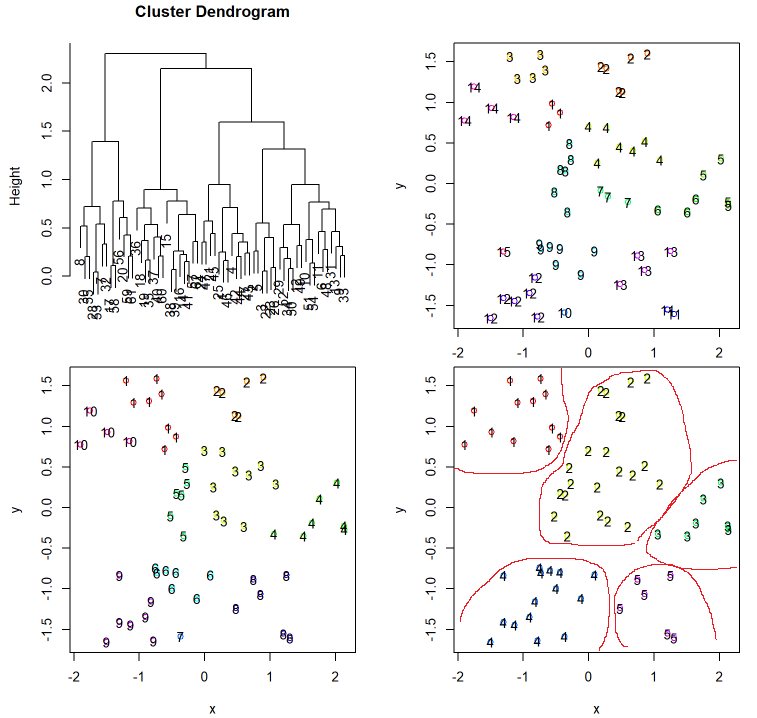
ウォード法
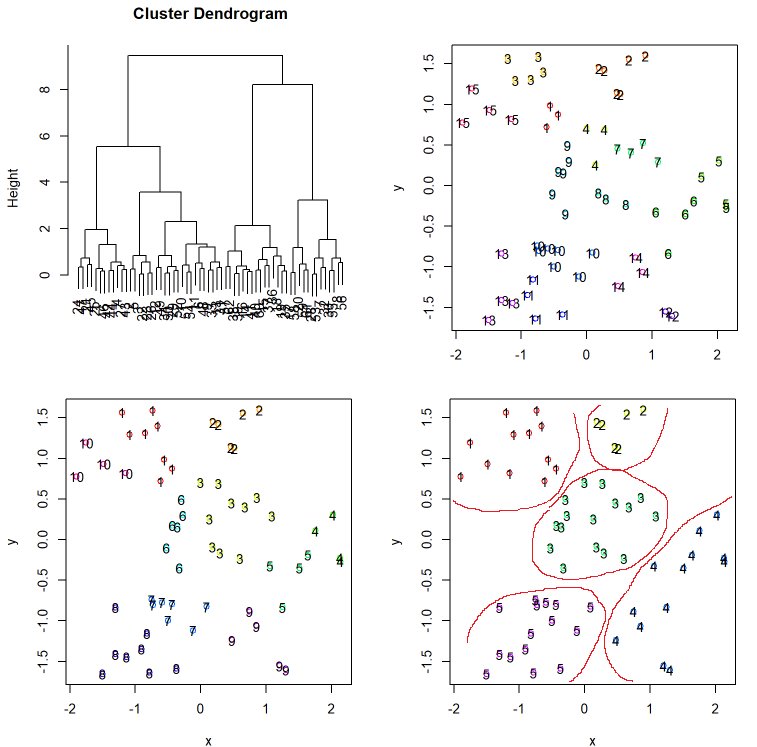
どちらとも計算量は多少増えるものの外れ値に強いため実用されることの多い手法です。
クラスタリングの注意点
今回の4手法の5分割Verだけ見てみても、結果はすべて異なっています。もちろんデータの性質にもよりますが、それだけ手法によって変わりやすいものなので、どういうクラスタリング結果になったかというのを評価するのは非常に重要です。
また、今回の結果だけ見ると最短距離法って駄目なの?と思われそうですが、例えば違うデータではこのような結果になりました。
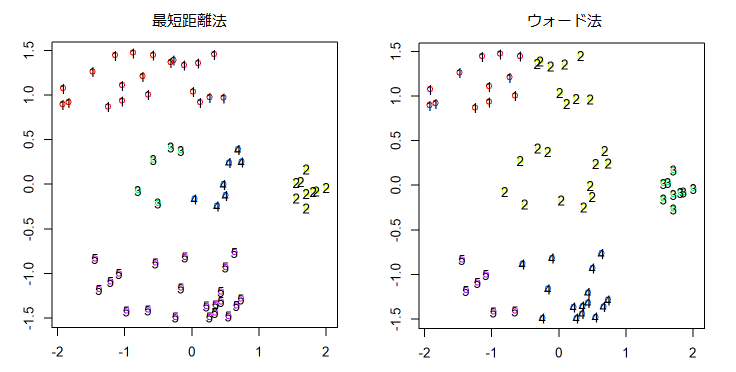
これも正解がないものなので、どちらが良いとも言えませんが、近くのものを吸収していくという性質がうまく人間の感覚と合うこともあります。
なので、どういったことを重視してグルーピングしたいのかということを考えながら手法を選びましょう。