本記事はQiitaの機械学習の数理 Advent Calendar 2018の8日目の記事です.
単語の「意味の広がり」を捉えられる単語埋め込み手法であるガウス埋め込みについて紹介します.
だいたいこの論文の説明です.
はじめに
もはやNLPの必須ツールとなったword2vec,というかSkipgramに代表される単語分散表現ですが,単語の意味のモデル化という意味ではいくつかの問題点もあります.
そのうちの一つが,「1つの単語に1つのベクトルを割り当てる」点推定になっており「単語の意味の広がりを捉えられない」という点です.
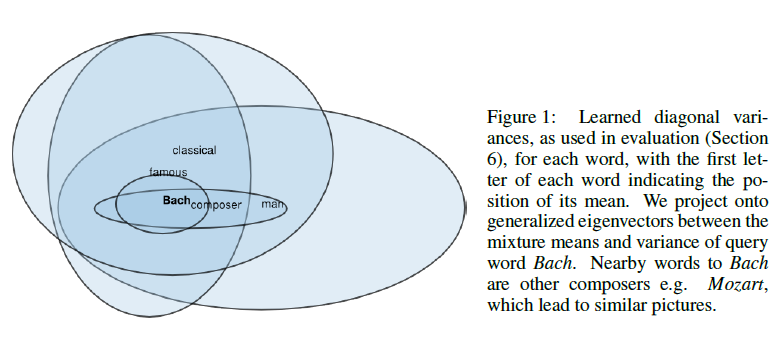
例えば下図に示すように,
- Bach $\in$ composer $\in$ man
- manは非常に広い意味をもつ
- composerはもう少し狭い
- Bachは人名なのでよりspecificな意味
といった単語同士の意味の重なりや包含関係をembeddingの空間上で分析したいケースがあります.
このような場合に使える単語埋め込み手法が「ガウス埋め込み」です.
具体的な利用例としては,今年の言語処理学会で発表された京大時武さんの論文にて時代の変遷に伴う単語の意味の変化の分析に使われています.
かくいう僕もこの論文を読んで「へ~ガウス埋め込み面白いな」と思ったのが今回取り上げた動機だったりします.
ガウス埋め込みのモデル
まず,各単語$w_{i}$にembedding空間上のガウス分布を割り当てます.
$$w_{i} = \mathcal{N}(x;\mu_{i},\Sigma_{i})$$
点ではなく確率分布で単語の意味をモデル化するわけですね.
ガウス分布の平均が単語分散表現で言う意味ベクトルに相当するもの,共分散行列がembedding空間上での分散(=意味の広がり)を表します.
現在の単語から周辺文脈の単語を予測するのはSkipgramと同様です.
似た文脈で出てくる単語は似た意味になるようなパラメータ$\mu_{i}$と$\Sigma_{i}$を得たいわけですが,
ここでパラメータ$\theta$のもとで単語$x$と$y$の類似度を測るエネルギー関数$E_{\theta}(x,y)$を導入します.
現在の単語を$w$,$w$と同一文脈に出現する文脈語を$c_{p}$,同一文脈に出現しない単語を$c_{n}$としたときに,
$$E_{\theta}(w,c_{p})>E_{\theta}(w,c_{n})$$
となるような$\theta$を得たいと.
そのために下記の損失関数$L$を考えます.
$$L_{m}(w,c_{p},c_{n}) = max(0, m-E(w,c_{p})+E(w,c_{n}))$$
これはRank-SVMなどで使われているmax-margin ranking lossというものです.
この$L$を最小化するように学習を行っていきます.
エネルギー関数の選択
エネルギー関数$E$に用いる関数には対称な類似度もしくは非対称な類似度を選ぶことが可能です.
対称な類似度:期待尤度
対称な類似尺度として非常に妥当なのが2つの独立なガウス分布のドット積ですが,これは共分散が計算できないのでここでは使えません.
そこで代替手段になるのが2つの分布自身の内積.(これを期待尤度と呼びます)
$$\int_{x\in \mathbb{R}^{n}}f(x)g(x)$$
ガウス分布の内積は以下で定義されます.
$$E(P_{i},P_{j})=\int_{x \in \mathbb{R}^{n}}\mathcal{N}(x;\mu_{i},\Sigma_{i})\mathcal{N}(x;\mu_{j},\Sigma_{j})dx = \mathcal{N}(0; \mu_{i}-\mu_{j},\Sigma_{i}+\Sigma_{j})$$
ガウス分布は安定分布なので,2つのガウス分布の畳み込みは別のガウス分布になります.
対数をとって,
$$\log \mathcal{N}(0;\mu_{i}-\mu_{j},\Sigma_{i}+\Sigma_{j})=-\frac{1}{2}\log\det (\Sigma_{i}+\Sigma_{j})-\frac{1}{2}(\mu_{i}-\mu_{j})^{\top}(\Sigma_{i}+\Sigma_{j})^{-1}(\mu_{i}-\mu_{j})-\frac{d}{2}\log(2\pi)$$
$\mu_{i}$と$\Sigma_{i}$それぞれについて偏微分して勾配を得ます.
\begin{align}
\frac{\partial\log E(P_{i},P_{j})}{\partial\mu_{i}} &= -\frac{\partial\log E(P_{i},P_{j})}{\partial\mu_{j}} = -\Delta_{ij}\\
\frac{\partial\log E(P_{i},P_{j})}{\partial\Sigma_{i}} &= \frac{\partial\log E(P_{i},P_{j})}{\partial\Sigma_{j}} = \frac{1}{2}(\Delta_{ij}\Delta_{ij}^{\top}-(\Sigma_{i}+\Sigma_{j}^{-1}))
\end{align}
ここで,
$$\Delta_{ij}=(\Sigma_{i}+\Sigma_{j})^{-1}(\mu_{i}-\mu_{j})$$
導出の過程で以下の公式を用いています.
\begin{align}
\frac{\partial}{\partial A}\log \det A &= A^{-1} \\
\frac{\partial}{\partial A}x^{\top}A^{-1}y &= -A^{-\top}xy^{\top}A^{-\top}
\end{align}
$$$$
$$$$
対数エネルギー関数の第2項は$\mu_{i},\mu_{j}$間のMahalanobis距離で,第1項は2つの共分散を単調増加させることにより距離が減少するのを防ぐ正則化項の働きをします.
この組み合わせにより,平均をより集中度を増すように押し上げ,尖ったピークを持つ分布となります.
非対称な類似度:KLダイバージェンス
エネルギー関数のもうひとつの選択肢が僕らのKLダイバージェンスです.
KLを使うとエネルギー関数に非対称性を持ち込むことができます.
KLを用いたエネルギー関数は下記で定義できます.
\begin{align}
-E(P_{i},P_{j}) &= D_{KL}( P_{j}||P_{i} )=\int_{x \in \mathbb{R}^{n}}\mathcal{N}(x; \mu_{i},\Sigma_{i})\log \frac{\mathcal{N}(x;\mu_{j},\Sigma_{j})}{\mathcal{N}(x;\mu_{i},\Sigma_{i})}dx \\
&= \frac{1}{2}(tr(\Sigma_{i}^{-1}\Sigma_{j})+(\mu_{i}-\mu_{j})^{\top}\Sigma_{i}^{-1}(\mu_{i}-\mu_{j})-d-\log\frac{\det(\Sigma_{j})}{\det(\Sigma_{i})})
\end{align}
マイナスがついているのはKLは確率分布の「差異」を表す量なので類似度に変換するためですね.
で,期待尤度の場合と同様にレッツ偏微分.
\begin{align}
\frac{\partial E(P_{i},P_{j})}{\partial \mu_{i}} &= -\frac{\partial E(P_{i},P_{j})}{\partial \mu_{j}} = -\Delta_{ij}^{'} \\
\frac{\partial E(P_{i},P_{j})}{\partial \Sigma_{i}} &= \frac{1}{2}(\Sigma_{i}^{-1}\Sigma_{j}\Sigma_{i}^{-1}+\Delta_{ij}^{'}\Delta_{ij}^{'\top}-\Sigma_{i}^{-1}) \\
\frac{\partial E(P_{i},P_{j})}{\partial \Sigma_{j}} &= \frac{1}{2}(\Sigma_{j}^{-1}-\Sigma_{i}^{-1})
\end{align}
ここで,
$$\Delta_{ij}^{'}=\Sigma_{i}^{-1}(\mu_{i}-\mu_{j})$$
導出の過程で以下の公式を用いています.
$$\frac{\partial}{\partial A}tr(X^{\top}A^{-1}Y)=-(A^{-1}YX^{\top}A^{-1})^{\top}$$
$$\frac{\partial}{\partial A}tr(XA)=X^{\top}$$
学習
$L$は非凸なので勾配法で最適化していきます.論文ではAdaGradを用いています.
さらに,ここで$\mu$と$\Sigma$に正則化を入れます.
$\mu$と$\Sigma$は異なる幾何的性質をもつので,それぞれ別の正則化を行います.
まず$\mu$は値が増大しすぎるのを防ぎたいので,L2ノルムを正則化項に用います.
$$||\mu_{i}||_{2}\leq C, \forall i$$
$\Sigma$は正定値を維持したいので,固有値$\lambda_{i}$が$[m,M]^{d}$の中に含まれるような制約を導入します.
$$mI\prec \Sigma_{i} \prec MI, \forall i$$
$\Sigma$が対角行列の場合は,対角要素にminとmax関数を適用することでこの制約を満たすことが可能です.
$$\Sigma_{ii} \Leftarrow \max(m,\min(M,\Sigma_{ii}))$$
特に期待尤度で学習する場合,共分散行列の固有値の下限のコントロールは重要です.
というのも,エネルギー関数が$\log \det$の項を含むので,分散が小さい場合に非常に大きな値になり,エネルギー関数の大部分をこの項が決めてしまうといった望ましくない現象が起きるからです.
使ってみるには
word2gaussというPython/Cython実装が公開されています.
僕もまだ動かそうとしている最中ですが,ひとまずWikipediaで学習してみようかと考えています.
動かせたらまた更新しようと思います.
まとめ
ガウス分布による単語埋め込み手法「ガウス埋め込み」を紹介しました.
単語の意味の分散(=広がり)的なものを捉えられるので,意味の広がりや多様性みたいなものを見たいときは使ってみるとよいかもしれません.