慶應義塾大学・株式会社Nospareの菅澤です.
今回は異質性のある因果効果とその推定方法について紹介します.
異質処置効果 (Heterogeneous Treatment Effect)
標準的な潜在アウトカム(potential outcome)の設定下での因果効果の推定を考えます.そのため,以下の変数を用意しておきます.
- $X$: 説明変数
- $T$: 処置変数 ($T=1$: 処置群, $T=0$: 対照群)
- $Y^{(T)}$: 処置$T$のもとでの潜在アウトカム
- $Y=TY^{(1)} + (1-T)Y^{(0)}$: 観測できるアウトカム
観測データとしては$(Y,X,T)$の三つ組です.
処置$T$の因果効果を測る指標として広く用いられているのは平均処置効果(ATE; average treatment effect)でして,以下のように与えられます.
\bar{\tau} \equiv E[Y^{(1)}-Y^{(0)}]
集団内には異なる特徴$X$を持った個体が存在していますが,ATEはその名の通り,集団内における平均的な処置効果を測っています.これは,平均的な特徴を持っている仮想的な個体に対する処置効果を測っている解釈することもできます.

上の図はATEのイメージ図です.異なる特徴量(図中で色が異なる個体)を持った集団に対してある処置を施した場合,ATEは平均的な特徴量を持った仮想の個体(図中で色が重なった個体)に対する処置効果を考えていることを表しています.
このように,ATEでは平均的な効果のみを考えていますが,現実的な問題では処置効果が各個体の説明変数によって異なる可能性が考えられます.そのような状況の例として
- ある治療を施した場合,患者の遺伝的な情報や生活習慣に応じて効き目が異なる
- ある広告を打った場合,受け手の属性によって効果が異なる
といったことが考えられます.
このように,説明変数$X$に応じて変化する形の処置効果をHeterogeneous Treatment Effect (HTE) または Conditional Average Treatment Effect (CATE) と呼ばれ,次のように定義されます.
\tau(X) \equiv E[Y^{(1)}-Y^{(0)}|X]
以下はHTEのイメージ図です.
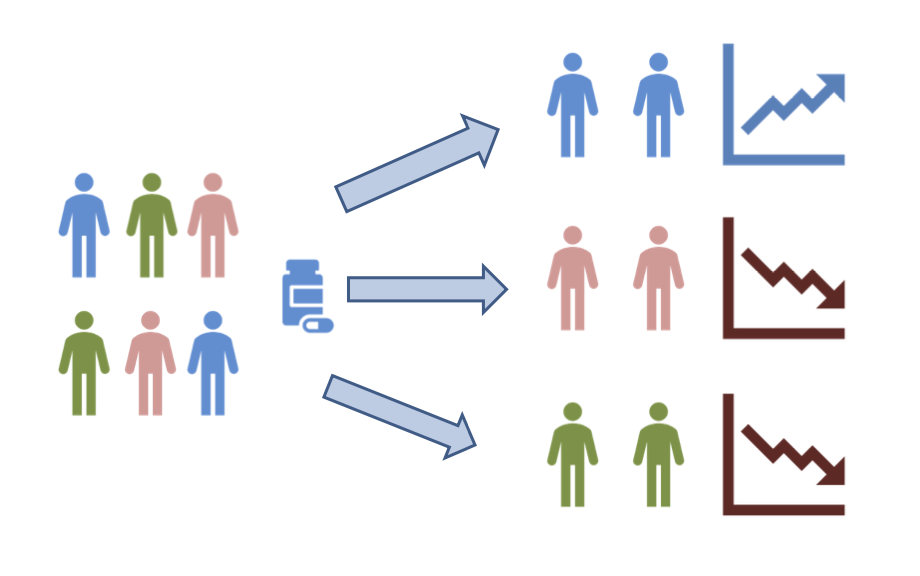
ATEとHTEの関係性で重要な点として,ATEが0だからと言ってHTEが必ずしも0にはならない点があります.例えば,正のHTEと負のHTEを持つ個体が混在している場合,ATEを考えると0になる可能性が考えられます.このように,ATEが0だからと言って因果効果がないと判断するのは時期尚早で,HTEまで考えることで思いがけない因果効果を発見できる可能性があります.
HTEを推定する方法
データからHTEを推定する方法としては様々なものが提案されています.以下では,$n$個のデータ$(Y_i, X_i, T_i)_{i=1,\ldots,n}$が得られていることを想定し,代表的な手法について概略を紹介します.
線形回帰モデル
最も単純な方法として,以下のような交差項のある線形回帰モデルを当てはめます.
Y_i=X_i^\top\beta + T_iX_i^\top\gamma + \varepsilon_i
このとき,HTEは$\tau(X_i)=X_i^\top\gamma$となるため,モデルパラメータを推定することでHTEを推定できます.簡単な方法でありますが,$X_i^\top\beta$や$X_i^\top\gamma$の構造がシンプルすぎるためモデル誤特定によるバイアスが生じる懸念があります.
機械学習 (またはノンパラメトリック回帰) を使う方法
線形回帰モデルのような単純な構造を避ける方法として,ノンパラメトリック回帰や機械学習的なアルゴリズムを用いてHTEを推定することも可能です.方法としては大きく2つあります.
-
(S-learner) $Y_i=f(X_i, T_i)+\varepsilon_i$を推定し,HTEを$\tau(X_i)=f(X_i, T_i=1)-f(X_i, T_i=0)$の形で推定します.
-
(T-learner) 処置群($T_i=1$の群)と対照群($T_i=0$の群)で別々に$f_1(X_i)\equiv E[Y_i|X_i, T_i=1]$および$f_0(X_i)\equiv E[Y_i|X_i, T_i=0]$を推定し,HTEを$\tau(X_i)=f_1(X_i)-f_0(X_i)$の形で推定します.
S-learnerおよびT-learnerはそれぞれ"Single"モデルと"Twin"モデルによってHTEを推定していることに由来します.回帰関数の推定にはXGBoostやランダムフォレストなど様々な方法を用いることが可能です.
また,前述の線形回帰モデルによる手法は,S-learnerの具体的な方法の一種とみなすことができます.
X-learner
X-learnerはT-learnerを進化させた方法でKunzel et al. (2019)で提案された方法です.以下のステップによってHTEの推定を行います.
注: 以下では$Y_i$や$X_i$が処置群と対象群の観測データであることを明確にするために$Y_i^1$および$Y_i^0$といった表記を用います. (これは潜在アウトカムではありません.)
-
(回帰関数の推定) T-learnerと同様に,両群において$f_1(X_i)\equiv E[Y_i|X_i, T_i=1]$および$f_0(X_i)\equiv E[Y_i|X_i, T_i=0]$を推定します.
-
(counterfactualの補完と残差の計算) $f_0(X_i^1)$および$f_1(X_i^0)$を計算し,残差$D_i^1\equiv Y_i^1-f_0(X_i^1)$および$D_i^0\equiv f_1(X_i^0)-Y_i^0$を計算します. $f_0(X_i^1)$は処置群のデータが対象群だった場合(counterfactual)の予測を考えていることに相当し,$D_i^1$は処置群における処置効果を意味します.
-
(2通りのHTEの推定) $D_i^1$および$D_i^0$の定義から$\tau(X_i)=E[D_i^1|X_i]=E[D_i^0|X_i]$が成立します.そこで,前のステップで計算された$D_i^1$および$D_i^0$を用いて2種類の条件付き期待値(回帰関数)を推定することで2種類のHTE推定量が得られます.それぞれ$\tau_1(X_i), \tau_0(X_i)$と表記します.
-
(HTE推定量の統合) ある重み付き関数$g(X_i)\in [0,1]$を用いてHTEを$\tau(X_i)=g(X_i)\tau_1(X_i)+(1-g(X_i))\tau_0(X_i)$の形で推定します.元論文では$g(X_i)$として傾向スコアを用いることを推奨しています.
X-learnerでは4つの回帰関数($E[Y_i|X_i, T_i=1]$, $E[Y_i|X_i, T_i=0]$, $E[D_i^1|X_i]$, $E[D_i^0|X_i]$)を推定することになりますが,ユーザーの好きな方法で推定することができます.(逆に選ぶ手法によって最終的なHTE推定量のパフォーマンスが変わってくるので慎重に選ばないといけないとも言えます.)
R-learner
Nie and Wager (2021)によって提案された方法です. HTEを推定するために,以下のロビンソン分解(Robinson decomposition)を用いています.
Y_i-m(X_i)=(T_i-\pi(X_i))\tau(X_i)+\varepsilon_i
ここで,$m(X_i)=E[Y_i|X_i]$はアウトカムの条件付き期待値で$\pi(X_i)=P(T_i=1|X_i)$は傾向スコアです.
2つの関数$m(X_i), \pi(X_i)$が所与のもとで,R-learnerは
\sum_{i=1}^n \Big[(Y_i-m(X_i))-(T_i-\pi(X_i))\tau(X_i)\Big]^2 + \Lambda_n(\tau(\cdot)))
を最小化する形でHTE$\tau(X_i)$を推定します.ここで,$\Lambda_n$は正則化項です.
実際は$m(X_i)$および$\pi(X_i)$は未知のため,観測データから推定したものを上記の損失関数に代入します.Nie and Wager (2021)では,観測データを分割し,$m(X_i), \pi(X_i)$の推定と$\tau(X_i)$の推定とで別々のデータを使う方法(一般にcross fittingと呼ばれる方法)を提案しています.
R-learnerでは合計3つの未知関数を推定することになりますが,基本的にどのような手法・モデルも使用可能です.
R-learnerのRパッケージはGitHubからダウンロードできます. (このパッケージにはX-learnerを実行するモジュールも含まれています.)
Causal forest
Wager and Athey (2018)によって提案された方法で, HTEを直接推定する形にカスタマイズしたランダムフォレストのアルゴリズムです.
T-learnerでは$f_1(X_i)$と$f_0(X_i)$の2つの回帰関数を推定しますが,興味のあるHTEはそれらの差分です.すなわち,$f_1(X_i)$と$f_0(X_i)$が共通に持っている回帰構造は差分を計算する段階で打ち消されるため,興味のない部分(局外パラメータ)となります.そのような局外パラメータの推定を経由せずに直接的にHTEを推定することができるのがcausal forestの特徴です.
causal forestはRのgcfパッケージで実行することができます.また,Wager and Athey (2018)ではcausal forestによるHTE推定量の漸近正規性を導出しており,推定だけでなく統計的推測(例えば95%信頼区間の計算)も可能です.
Bayesian causal forest
ランダムフォレストのベイズ版であるBayesian additive regression tree (BART)をHTE推定に適用した方法でHahn et al. (2020)によって提案されました.
観測データに対して以下のモデルを考えます.
Y_i=\mu(X_i,\hat{\pi}_i)+\tau(X_i)T_i+\varepsilon_i
ここで,$\hat{\pi}_i$は傾向スコアの推定値です.上記のモデルで$\mu$および$\tau$が未知関数となりますが,これに対してBART事前分布を導入し,マルコフ連鎖モンテカルロ法により$\tau(X_i)$(HTE)の事後サンプルを生成することで点推定や信用区間の計算を行うことができます.
この方法は部分的にcausal forestのベイズ版だと捉えることができますが,漸近論に頼るcausal forestと比べて有限サンプル下でより良い性能を示すことが論文中の数値実験等で示されています.
Bayesian causal forestはRのbcfパッケージで実行することができます
Bayesian causal synthesis
最後に,関連した自分の研究について紹介します.これまで紹介したように,HTEを推定するアルゴリズムは非常に多く存在します.一方で,どんな状況でも精度の高い普遍的なアルゴリズムがないことが経験的に知られています.その場合,単一のアルゴリズムやモデルを考えるのではなく,複数のモデルによるHTEの推定結果を「柔軟に」統合する枠組み があると有用であると考えられます.
Sugasawa et al. (2023)では,ベイズ的予測統合の技術を用いて,複数のHTE推定量を統合する方法を提案しています.
そのために,以下の階層モデルを考えます.
Y_i=m(X_i, \hat{\pi}_i)+T_i\Big[\beta_0(X_i)+\sum_{j=1}^J\beta_j(X_i)f_j(X_i)\Big]+\varepsilon_i
ここで, $J$は統合するHTE推定量の数,$f_j(X_i)$はHTE推定量の分布(推定値と漸近分散をそれぞれパラメータにもつ正規分布など), $\beta_j(X_i)$が各HTE推定量 (モデル)に対する重みです.重要な性質として,モデルの重み$\beta_j(X_i)$が定数ではなく,$X_i$の関数になっています.
上記のモデルにおいて,HTEは
\tau(X_i)\equiv \beta_0(X_i)+\sum_{j=1}^J\beta_j(X_i)f_j(X_i)
となります.$\beta_j(X_i)$にガウス過程の構造を導入し,マルコフ連鎖モンテカルロ法で$\tau(X_i)$の事後サンプルを生成することで,統合型HTEの点推定値や信用区間を計算することができます.
おわりに
今回は異質性のある因果効果とその推定方法について紹介しました.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.
