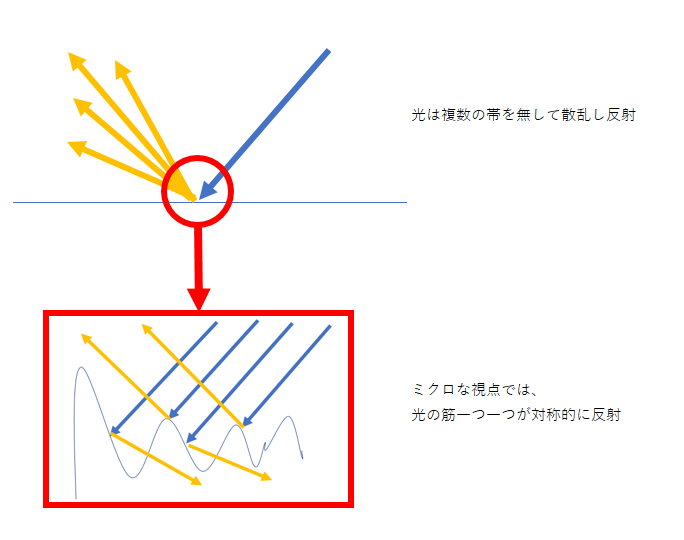
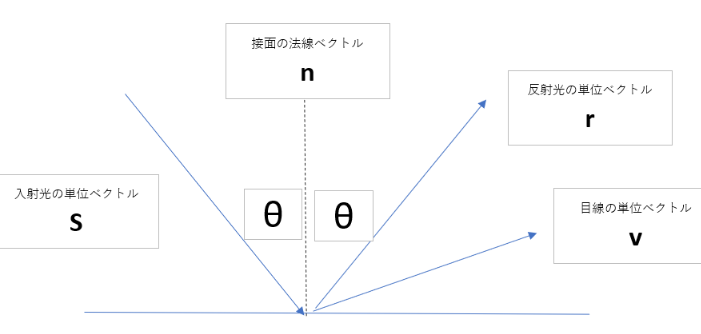
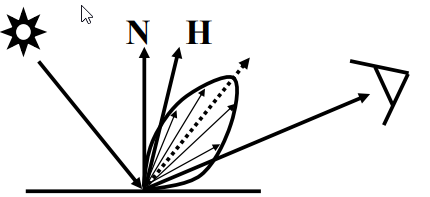
去年Googleが発表した「Total Relighting」
一枚の画像から、人物を切り出し、背景に合わせて人物のライティングを自動で調整する手法。
・・・らしいのですが。すごいですよね。
フォトリアルというと、最近は3D分野の目覚ましい発展を連想しますが、
3Dはどうしても装置や機材に依存するイメージが付きまといます。
もしもiphoneなどの単眼カメラで実現できるようになれば、
表現の世界はさらに次のステージに進めそうです。
ということで今回はそんな「フォトリアル」な世界について勉強します。
できるだけ数式と実際のソースに基づいて理解を深めていきます。(目標)
このページはちまちまと更新していくと思うのでよろしくお願いします。
2022/04/08 新規作成
2022/04/14 RayTracig(物体とカメラの設定編)を追加
2022/04/16 RayTracig(光と色編)を追加
参考:
https://google.github.io/filament/Filament.html
https://www.robots.ox.ac.uk/~att/index.html
https://tokoik.github.io/gg/ggnote07.pdf
https://shikihuiku.wordpress.com/2012/07/06/brdfirradianceradiance%E3%81%AE%E5%AE%9A%E7%BE%A9/
https://marina.sys.wakayama-u.ac.jp/~tokoi/
https://learnopengl.com/Code-repository
https://github.com/rafael-fuente/Python-Raytracer
https://pbr-book.org/3ed-2018/Introduction/Photorealistic_Rendering_and_the_Ray-Tracing_Algorithm
https://www.scratchapixel.com/lessons/3d-basic-rendering/introduction-to-ray-tracing/how-does-it-work
http://omilab.naist.jp/class/CV/2019/2019-CV-No5-Reflection-ForReport.pdf
概要的の整理
リアルな世界を再現するからには、リアルの世界の色の仕組みを勉強します。
吸収/反射と色
世の中には赤いポスト、黄色い手ぬぐい、青い封筒と、世の中は様々な色にあふれています。
コンピューターグラフィックの世界ではこれらの色をRGBなどの数値で扱うわけですが、
物体の色が常に同じRGBの数値で表されるかといえば、そうではありません。
例えば、日本の国旗の「赤」はRGBで言えば「188, 0, 45」です。
しかし写真で撮影したときに常に「188, 0, 45」になることはありません。
暗い場所で見れば濃くて暗い赤になるし、夏の青空の中で見ると少し黄色がかったRGBの数値を示すことでしょう。
色というものは、環境や様々な要因によって変化します。
一例として、昔ネット上で話題になった「この服の色は何色なのか」の例の画像を見てみます。

この服は実際には「青と黒」の服です。
青い物体というものは赤い波長の光を吸収する性質があります。
原理としては、一般的な光の強さであれば、青い物体は青い光だけを反射して、
赤い光を吸収した結果、青い色に見えます。
ではなぜこの服は赤寄りの黄色になるのでしょう。
青い物体は、赤い暖色系の光を「強く」浴びると、今まで吸収し切れていた赤い光が飽和し、吸収しきれなくなります。
例えるなら、コーヒーに砂糖をいれすぎると砂糖が溶け切らないのと同じですね。
その結果、吸収できなかった赤い波長の光が反射し始めるわけです。
人は反射した光を眼球でとらえることで「色」を見出すので、
反射された一部の赤い光もとらえ始めたことで、物体は青から赤よりに代わるのです。
反射率と色
上述の通り、物体は特定の光の波長を吸収します。
いわば、我々が目にする光は物体によって加工された光とも言えます。
例えば、100%のエネルギーをもった光を照射したときに、50%を反射、50%を吸収したのだとすれば、
吸収された分、光は削減されるので直感的には「暗く」感じるわけです。

上のりんごは、ほぼ100%光を吸収する塗料を塗ったらしいのですが、
ご覧の通り真っ黒になって光は吸収されていますね。
さて、「物体が光を吸収する = 光は物体によって加工される」
ということを踏まえて、一つの仮定をしてみましょう。
もしも物体が光を吸収することなく「完全に反射」したらどうなるでしょうか。
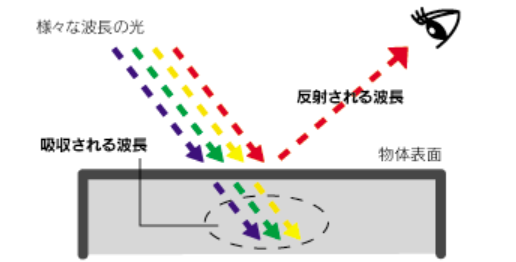
復習です。「吸収/反射と色」にて説明した通り、物体の色というものは、
物体固有の割合で特定の波長が吸収されることで生まれます。
赤い物体であれば、赤い以外の波長の光を吸収するので赤い色に見えます。
「もしも物体が完全に反射したらどうなるか」
結論から言えば、上の画像の左端、周りの景色がそのまま映り込みます。
もしも吸収が発生せずそのまま反射されるのであれば、
その物体に差し込まれた光は加工されないまま人の目に到達します。
空の青い光もそのまま、マクドナルドの看板から発される赤と黄色もそのままです。
なので、鏡のように周りの景色の色がそのまま見えます。
逆に、光を著しく吸収すれば画像の右端の通り、光を吸収しすぎた結果暗くなり、
見える色はその物体が吸収を不得意とする波長の色が見えるようになります。
吸収によって光源の光は大きく損なわれるので、周囲の景色は鮮明には見えなくなることでしょう。
正反射と色
私たちは小学校の理科の授業で光の反射について勉強しました。
記憶の通りなら、まっすぐ照射された光がまっすぐな面に当たって対称的に光が進むはずです。
しかし実際には光は広がるように様々な範囲の角度で反射します。
これを図解します。
凹凸のある面に光が当たると、光はある範囲を散乱するように反射します。(上)
この図だけ見ると、小学生のときにならったことが嘘のように思えてきます。
全然対称的に反射していません。
ですが、これはどちらも正しいのです。
ミクロな視点で表面を見ると、面はわずかに凹凸をはらんでいるので、(下)
小さな小さな光の単位は小さな凹凸にぶつかることで様々な方向に反射し、
その結果、光は散乱してみえるのです。(ここでいう散乱は光の散乱とは違う)
小学生の頃に習った反射を正反射。
凹凸の表面によって広がるように反射する光を正反射成分(Specular lobe)といいます。
法線と色

(参考:https://area.autodesk.jp/column/tutorial/3ds_max_kitchen_stadium/micro_surface/)
正反射成分の広がりが多い場合は表面の凹凸がはげしく粗い(roughness)表面(左)
正反射成分の広がりが少ない場合は表面がツルツルしている表面で、正反射の光がよく見えます(右)。

(参考:https://learnopengl.com/Advanced-Lighting/Normal-Mapping)
正反射成分をすべて把握する、ということは
言い換えれば、表面がどのような凹凸になっているかを把握するということです。
完全なフォトリアルを目指すならば、表面の凹凸を完全に定義しなければなりません。
上の図の左を見てみます。
表面の凹凸を考慮せずに光を照射しています。画像を見ると質感が損なわれていることがわかりますね。
例えるなら、お店の張り紙にレンガのシールを貼った壁、という感じです。ツルツルしてそうです。
上の図の右を見てみます。
最近では、表面の凹凸をテクスチャ画像と一緒に定義して「法線マップ(Normal mapping)」を
読み込ませることで、表面がどのように凹凸しているか決定し、反射の向きを計算します。
法線に基づいて一本一本の光がどの角度で反射されているか計算されているので、
リアルな反射が再現されいます。
拡散反射と色
https://onl.bz/PtBzWJx
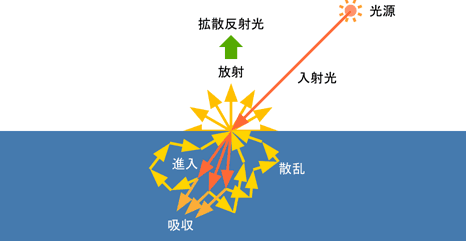
拡散反射光は、物体表面上であらゆる方向に向けて光が反射する反射光です。
「法線と色」でもあらゆる方向に反射する正反射成分について述べましたが、拡散反射とは異なります。
拡散反射は、内部に入射した光が物体内部で反射しつづけることで、
様々なベクトルを持った光が再び境界面から飛び出します。
拡散反射の特徴は、
「物体内部から飛び出した光」
「光の向きはあらゆる方向に散乱している」
と言えるでしょう。
一度物体の中を通って放出されるので、光の波長が内部で吸収されます。
拡散反射光はいわゆる「物体の固有色」を帯びた光になります。
例えば人の肌のような透き通った物体であれば、肌の下を流れる「血」の中で光たの吸収・散乱を繰り返すことで、
肌表面から発生する拡散反射光は血の色を反映した赤が現れます。
拡散反射は光があらぬ方向に放出される分、上図のように少しぼんやりした光になります。
これが例えば、拡散反射光が極端にない場合どうなるかといえば、
内部で散乱して反射する光はなくなり、表面で綺麗に反射された光だけが
発生する状態、すなわち「法線と色」で述べた「正反射成分」だけが残ります。
光が散乱しない分、輪郭は明確であり、かつ、拡散反射光のように内部で光の
吸収が行われない分、光の色が色濃く特徴として発生します。
余談ですが、「正反射成分」は「鏡面反射光」とも呼ぶようです。
RayTracing
聖書では、「光あれ」という一言から世界が始まりました。
その言葉の通り、我々が見える色は、太陽光が光を照射して、
物体が反射を行うことで初めて我々の世界は始まります。
これを工程ごとに分けると、以下のとおりです。
1.太陽が光を発射
2.物体が光を反射
3.反射した光を眼球がキャッチ
現実の物理世界では上記の工程で人の視界に「色」を発現させます。
パソコン上でこれを再現しようと思えば、無数に放たれる光線をすべて計算して、
全ての物体がどの角度からどう当たるかを計算して、どの角度で眼球に反射するかを計算することになります。
言うまでもなく、途方もない計算量です。
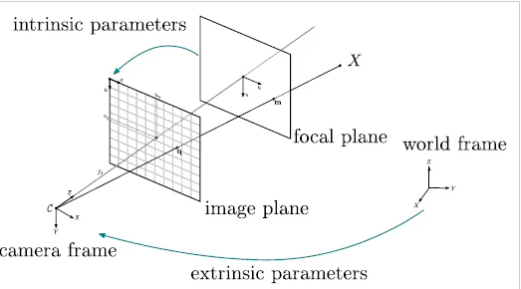
そこで視線(Ray)という考え方を導入します。
要するに、視界に映る領域だけを計算しましょう、という考えです。
上の図は、人の目の見え方をピンホールカメラで模したものです。
焦点距離の位置に発生する[image plane]で人は実際の映像を一枚の画像のようにとらえます。
コンピュータでの処理を念頭に置いたとき重要になることは、
[image plane]の向こう側にどれだけ世界が広がっていようとも、我々の世界は[image plane]の世界だけということ。
[image plane]に映らない要素は、視線に映らない限り計算しても不要なのです。
仮にこの[image plane]が720×420の解像度なのであれば、
302400ピクセルの数ぶんだけ計算しよう、というのがレイトレーシングの基本的な考え方になります。
光の計算
光の計算をいくつか見てみます。(この辺が一番気になっていた)
参照:https://www.cs.cmu.edu/afs/cs/academic/class/15462-f09/www/lec/lec8.pdf
前提知識:放射束 / 輝度 / 照度
「放射束」
「輝度」
「照度」
言葉だけ書いてもわかりにくいので、それぞれの単語の意味について簡単に解説します。
それぞれ意味合いや計算が異なりますが、どれも光の強さを表したものです。
単位は以下の通り。
「放射束」=ルーメン
「輝度」 =ルクス
「照度」 =カンデラ
家電家さんで見たことがあるかもしれない言葉ですね。
誤解を恐れずに言えば、
放射束、入射光の放射輝度、反射光の放射照度とは、「光の照射~物体衝突~反射」の一連の流れを
マラソンで例えたようなものになります。
マラソンしたとき、
1.最初どれくらいの体力があって(放射束)、
2.基本的な走力(輝度)がそこそこある光が、
3.坂を登り始めたときにどれくらいのペースで衰退するか(照度)。
これら一連の流れを表したものが放射束、入射光の輝度、反射光の照度です。
以下に詳しく見てみます。
1.放射束は光そのものの強さです。光のすべての総量となります。
マラソンに例えるなら体力のようなものでしょうか。
体力があればあるほど長く走れるし、
ラストスパートで一気にダッシュをかけることもできます。
いわば、その人の走力を評価するための「絶対的な総量」といえます。
2.輝度はその光の「能力値」です。
ある領域(面積)にたいしてどれだけ強い光(放射束が高い光)を当てられるかを数値化したものです。
ある面積をどれだけあかるくできるかは、光を評価する上でとても大切です。
例えば、
放射束がとても高い光2つの光を想定します。
1つは、ある一点の方向に光を照射するポイントレーザー。
もう一つは、全ての方向に対して光を分散させるディフューズライト。
この光のどちらが明るいかといえば、
ポイントレーザーのほうが人間の目には明るく見えるでしょう。
ディフューズライトはせっかくのパワーを拡散させてしまってるので、比較的暗くなってしまいます。
マラソンに例えるなら瞬発力。
早く走ったときにどれだけ早く走れるかを表したものといえます。
3.照度
ある領域(面積)にたいしてどれだけ強い光(放射束が高い光)を当てられるかを数値化したものです。
・・・と書いた通り、輝度と同じ説明になります。
ただ根本的に異なるのは、照度の場合は距離による減衰が加えられている点です。
マラソンで例えれば、
坂道を走ったときにどれだけ元気に坂道を登り続けられるかを数値にしたものになります。
誤解を恐れずに言えば、
入射光の輝度は、衰退を考慮する必要もないほど強い日差しの太陽の光を想定し、
反射光の照度は、物体に反射して距離とともに強さが劣化していく物体からの反射光を想定します。
これらの単語は、光を計算するうえで重要です。
さっそく次項でつかっていきましょう。
BRDF
https://www.cs.cmu.edu/afs/cs/academic/class/15462-f09/www/lec/lec8.pdf
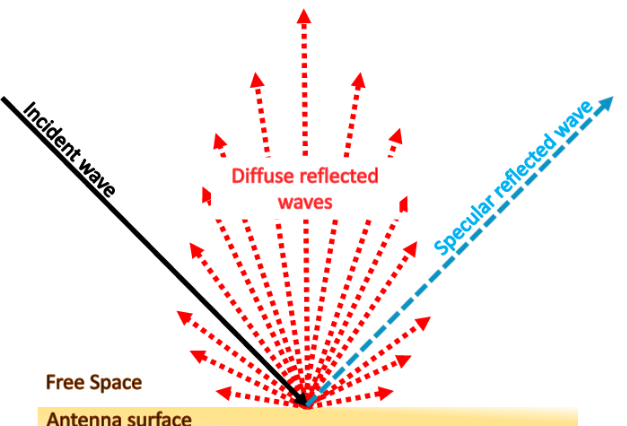
拡散反射を計算する上で把握しなければならないことは、
光が入射したとき、どの角度にどれだけの強さの光が発生するかということです。
この性質をBRDFと呼ばれる関数で表現します。
BRDF(\theta_{in},\phi_{in},\theta_{out},\phi_{out}) = \frac{L_{in}}{E_{out}}
$\theta_{in}$は法線に対する光の入射角度、$\phi_{in}$は入射光の放射束、
$\theta_{out}$は法線に対する光の反射角度、$\phi_{out}$は反射光の放射束、
$L_{in}$は入射光の輝度、$L_{in}$は反射光の照度です。
この式の示すところはつまり、
入射光、反射光の性質がわかれば、入射光に対して反射光がどれだけ減衰したかがわかるようになります。
この関数を完全に数式化することで、拡散反射を制御します。
プログラミング的に言えば、
関数という言い方よりも変換テーブルのイメージが近いのかもしれません。
入射された光の強さ・角度を取得して、視線に向かう角度を計算すれば、
反射光の強さが計算できます。
diffuse (拡散反射光)
Lambertian BRDF
おそらく最もポピュラーなランバートモデルについてみてみます。
拡散反射は、物体の性質によってどのように拡散するか未知数の存在ですが、
ランバートモデルではどの角度にも同じ強さで光が反射することを想定して計算します。
BRDFは以下の通り。
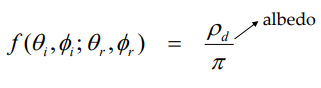
https://www.cs.cmu.edu/afs/cs/academic/class/15462-f09/www/lec/lec8.pdf
この式の意味するところはつまり、光の角度とか強さに関係なく、
入射光に対する反射光の減衰は一定だよ、ということを示します。
$\varrho_{d}$は定数で表されたアルベド。入射光100が反射光50で表されるなら、100/50=2のように表されます。
それでは、入射光の輝度を試しに計算してみましょう。
BRDF(\theta_{in},\phi_{in},\theta_{out},\phi_{out}) = \frac{L_{in}}{E_{out}}\\
\frac{L_{in}}{E_{out}} = \frac{\varrho_{d}}{\pi}\\
L_{in}=\frac{\varrho_{d}}{\pi}E_{out}
照度$E$には、斜入射光特性(コサイン特性)があります。
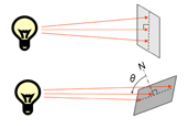
https://www.ccs-inc.co.jp/guide/column/light_color/vol08.html
照度は入射各$\theta$の$cos$に比例して変化するという特性です。
よって、$A$を光が照射される面積とすれば、(光を最小単位の一本の線とみなして計算するなら無視してもいいかも?)
L_{in}=\frac{\varrho_{d}}{\pi}\frac{\phi_{in}}{A}cos(\theta)
つづけて内積の公式、
$a\cdot b = |a||b|cos(\theta)$
より、aとbのベクトルを入射する光の単位ベクトル$s$、法線ベクトルの単位ベクトル$n$と仮定すれば、
以下の式が得られます
L_{in}=\frac{\varrho_{d}}{\pi}\frac{\phi_{in}}{A}n\cdot s
これが、入射光の輝度の計算式となります。
Specular Reflection( 正反射/鏡面反射 )
正反射。「正反射と色」では、粗い面での正反射について書きましたが、
ここでは滑らかで平らな板での正反射を想定しましょう。
Phong BRDF
まずは先ほどのランバートによる拡散反射。
L_{diffuse}=\frac{\varrho_{d}}{\pi}\frac{\phi_{in}}{A}n\cdot s
L_{diffuse}=K_{d} (n\cdot s)
$\frac{\varrho_{d}}{\pi}\frac{\phi_{in}}{A}$は定数で表せるので、$K_d$と定義します。これが、拡散反射光を現した式です。
これに、正反射/鏡面反射した光を加えれば下記式となります。
L =L_{diffuse} + L_{spectral}\\
次に、$L_{spectral}$を定式化しましょう。
Phongは正反射/鏡面反射した光として、以下のように定義しました。
L_{spectral}=K_{s} (r \cdot v)^{n}
定数$n$は定数です。$n$が小さいほど、鏡面反射の成分は強くなります。
よって、拡散反射と鏡面反射を合わせて
L =L_{diffuse} + L_{spectral}\\
L =K_{d} (n\cdot s) + K_{s} (r \cdot v)^{n}
・・・と、いうのがPhongモデル。
実はこの計算は、現実の物理現象に基づいたものではありません。
「目線のベクトル$v$と反射光のベクトル$r$の角度が近ければ近いほど、鏡面反射の成分は強くなる」
という性質をもとに、内積によって計算上でその性質が成り立つようにしただけで、現実に即した計算ではありません。
Blinn-Phong BRDF
L_{spectral}=K_{s} (r \cdot v)^{n}
Phong は現実に即した計算ではないのですが、勉強がてらそこから派生したBlinn-Phongも勉強します。
反射光$r$と目線$v$のベクトルの内積に対するべき乗で求めるのがPhongモデルですが、
反射光をいちいち求めたうえで、目に入ってくる反射成分を求めることは、
計算コストや推定の問題上できるだけ避けたい問題です。
ならもっと単純化しましょうよ、というのがBlinn-Phong。
$r$は使わずに、把握しやすい入射光$S$と視線方向$V$を使います。
L_{spectral}=K_{s} (r \cdot v)^{n}\\
L_{spectral}=K_{s} (n \cdot h)^{n}
$h=(s+v)/2$より求められる式です。算出家庭は省略。
RayTracing(詳細)
物体とカメラの設定編
https://qiita.com/akaiteto/items/dc829bb92e52471c5afa