More than 1 year has passed since last update.

これから更に流行るであろうフォトリアルな世界について勉強しよう　物体とカメラの設定編

Last updated at 2022-04-15Posted at 2022-04-14

去年Googleが発表した「Total Relighting」
一枚の画像から、人物を切り出し、背景に合わせて人物のライティングを自動で調整する手法。

・・・らしいのですが。すごいですよね。
フォトリアルというと、最近は3D分野の目覚ましい発展を連想しますが、
３Ｄはどうしても装置や機材に依存するイメージが付きまといます。
もしもiphoneなどの単眼カメラで実現できるようになれば、
表現の世界はさらに次のステージに進めそうです。

ということで今回はそんな「フォトリアル」な世界について勉強します。
できるだけ数式と実際のソースに基づいて理解を深めていきます。（目標）

参考：
https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-overview/light-transport-ray-tracing-whitted
https://msyksphinz.hatenablog.com/entry/2020/06/26/040000
http://webcache.googleusercontent.com/search?q=cache:qdi9_qbsG0QJ:kanamori.cs.tsukuba.ac.jp/jikken/inner/reflection_refraction.pdf+&cd=2&hl=ja&ct=clnk&gl=jp
https://www.cs.utexas.edu/users/fussell/courses/cs384g-fall2011/lectures/lecture11-Drt.pdf
https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-generating-camera-rays

ここまでの流れ

1.概要編
- 「こんなことやるんだー」という概要
  - https://qiita.com/akaiteto/items/a687cc7e855e40d706f9

RayTracing

RayTracingってなに？
RayTracingは光と物体の関係をシミュレーションすることで、リアルな世界を疑似的に再現する手法の一つです。
この記事では、RayTracingの一連の流れを踏まえたうえでの具体的な計算方法を勉強します。
https://github.com/rafael-fuente/Python-Raytracer

数式ばかりだと実勢に組む時にイメージがつかないので、上記のソースをベースに勉強します。
「Python-Raytracer」というプロジェクトは、RayTracingを実装したソースです。（私の作ったものではありません）
外部のライブラリに頼らず全部一から作成しているので、環境構築がものすごく楽で勉強におすすめです。すごい。

pip install pillow
pip install numpy

↑上記のライブラリがpythonの環境に入っいて、python3.6i以上なら基本的に動くと思います。
本記事では、「Python-Raytracer」のexample.pyを下記のように書き換えて、
拡散反射がどのような計算のもとでRayTracingされるかを見てみます。

test.py

from sightpy import *
# https://github.com/rafael-fuente/Python-Raytracer

# 物体の設定
diff_material =Diffuse(diff_color = rgb(0.9, 0, 0.1),diffuse_rays = 40)

# 背景色の設定
Sc = Scene(ambient_color = rgb(0.05, 0.05, 0.05))

# カメラの設定
angle = -np.pi/2 * 0.3
Sc.add_Camera(look_from = vec3(2.5*np.sin(angle), 0.25, 2.5*np.cos(angle)  -1.5 ),
			  look_at = vec3(0., 0.25, -3.),
	          screen_width = 400 ,
	          screen_height = 300)

# 光の設定
Sc.add_DirectionalLight(Ldir = vec3(0.52,0.45, -0.5),  color = rgb(0.15, 0.15, 0.15))
Sc.add(Sphere(material = diff_material, center = vec3(-.75, .1, -3.),radius =  .6, max_ray_depth = 3))

# 背景画像の設定
Sc.add_Background("stormydays.png")

# レンダリング実行
img = Sc.render(samples_per_pixel = 6)
img.save("EXAMPLE1.png")
img.show()

1.物体の設定
- 1_1.物体の形状
- 1_2.物体の色
  - （１）物体が単色の場合
    - 単色の色を設定
  - （２）物体がテクスチャの場合
    - テクスチャのUV座標・物体の3D座標より色を取得
- 1_3.物体の法線
2.人間の視線と物体の衝突点
- 2_1.衝突点
3.カメラの設定
- 3_1.座標について
- 3_2.視線位置（origin）の計算
- 3_2.視線方向（ray.dir）の計算
4.光の設定
5.反射光の設定
- 5_1.拡散反射光
  - 5_1_1. 接点の未加工の色の設定
  - 5_1_2. 拡散反射の設定
    - 拡散反射光のベース色の設定
    - 拡散反射光の本数の設定
    - 拡散反射光の分布の設定
    - 接点に対する拡散反射光の色の計算
  - 5_1_3. 最終的な色の計算

今回やること

今回は
1.物体の設定
2.人間の視線と物体の衝突点
3.カメラの設定
まで行います。

1.物体の設定

とにもかくにも物体の定義です。目に映る物体を作ることから始めないと、
世界をシミュレートすることはできません。
物体を定義するために必要なものは、「形状」「色」「法線」となります。
以下に詳しく見てみましょう。

1_1.物体の形状

ゲームだと様々な形状の物体が出てきますが、複雑な形状だと
「法線」「テクスチャ」「衝突点」の計算が面倒だったり、(これらの用語は後々説明します。)
手作りで一つずつ定義しないといけない場合があります。

本記事では、物体を球体に限定することで、面倒な計算を省き、
計算処理全体の概要の把握を優先します。

1_1.物体の色

物体は物体固有の割合で光の波長を吸収することで、物体独自の色、すなわち「固有色」を生み出します。
ここでは、３Ｄ化された物体から色を取得する方法について整理します。
さて、２Ｄ画像から色を取得する場合は、画像のピクセルの座標(xy)を指定して色を取得します。シンプルですね。

そして３Ｄの場合も同様、３Ｄ座標(xyz)を指定して色を取得することになります。

「３Ｄだろうと２Ｄ画像だろうと座標からそのまま取得すればいいんじゃない？」と簡単に思いがちですが、
仮想的に再現される３Ｄデータだとそう簡単にはできません。

２Ｄ画像の場合、すべてのデータが画像ファイル一つで完結しているので、座標を指定すれば簡単に取得できます。
それに対して３Ｄデータの場合は、３Ｄの構造データと２Ｄの画像データ２つから構成されているので手間が発生します。

ということで、これらを踏まえて、２つのケースを見てみましょう。

（１）物体が単色の場合

ソースを抜粋します。

extract.py

diff_material =Diffuse(diff_color = rgb(0.9, 0, 0.1),diffuse_rays = 40)

ソース上では、物体の色をrgb(0.9, 0, 0.1)と指定しています。
物体はrgb(0.9, 0, 0.1)で指定された値で染められた単色の物体になります。

このケースでは２Ｄ画像と連動していません。
なので、物体表面のポイントが何を示そうとも、色は「(0.9, 0, 0.1)」となります。
(※余談。この数字は255で正規化されています。見慣れたRGBの形式だと（229,0,23）になります。)

（２）物体がテクスチャの場合

ソースから必要な部分を抜粋します。

extract.py

        # 1.物体表面の座標(hit)から、UV座標を計算
        M_C = (hit.point - self.center) / self.radius
        phi = np.arctan2(M_C.z, M_C.x)
        theta = np.arcsin(M_C.y)
        u = (phi + np.pi) / (2*np.pi)
        v = (theta + np.pi/2) / np.pi

        # 2.UV座標とテクスチャ画像より、物体表面の座標(hit)の色を計算
        # self.img はテクスチャ画像 , uvは物体表面の三次元座標に対するUV座標
        im = self.img[-((v * self.img.shape[0]).astype(int)% self.img.shape[0]) , (u   * self.img.shape[1]*self.repeat).astype(int) % self.img.shape[1]  ].T
        color = vec3(im[0],im[1],im[2])

いきなりソースをはってもわからないので、
　　1.物体表面の座標(hit)から、UV座標を計算
　　2.UV座標とテクスチャ画像より、物体表面の座標(hit)の色を計算
上記の２段階に分けて記載します。

一般的なゲームでは３Ｄの物体に画像を張り付けることで質感や色や柄を再現します。
この時の画像をテクスチャといいます。

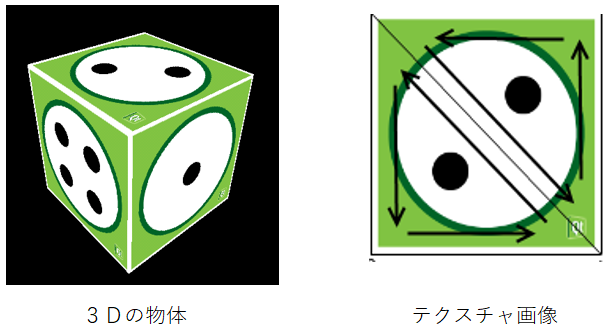
３Ｄ化された物体はテクスチャ画像で身を包んでおり、
サンプルソースの中では、以下のように３次元座標(xyz)から色を取得します。

１．３次元座標(xyz)からUV座標を取得
２．UV座標より、通常の画像の座標(x､y)を取得
３．画像の座標(x､y)より画像の色を取得

UV座標の概念について触れつつ、上記の工程を一つずつ見ていきます。

1.物体表面の座標(hit)から、UV座標を計算

UV座標とはなんだろう？UV座標というのは↓こういうやつ。
https://entry.cgworld.jp/terms/UV%E5%BA%A7%E6%A8%99%E7%B3%BB.html

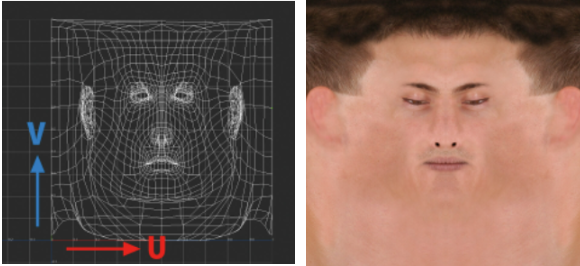
UとVの座標はそれぞれ0～1の間の数値で表されます。↑をみると一見画像のようですが、
通常のテクスチャ画像とは違った目的の画像となります。
それではUV用の画像の目的とはいったい何か整理しましょう。

例えば、丸い地球の立体に対して、我々が見慣れた四角い地図を張り付けようとしたら、
どうしたって余る部分が出てきたり、地図が張れない領域が出てきます。
現実世界であれば、地図を変形させる必要がでるでしょう。

そこで導入するのがUV座標という考え方です。
画像を引き延ばしたり縮めたりして、UVという縦と横の座標で表します。
これにより、歪みや余ったりする部分を発生させることなく、
３Ｄの物体に「綺麗に」色をマッピングさせることができるようになります。

extract.py

        # 1.物体表面の座標(hit)から、UV座標を計算
        M_C = (hit.point - self.center) / self.radius
        phi = np.arctan2(M_C.z, M_C.x)
        theta = np.arcsin(M_C.y)
        u = (phi + np.pi) / (2*np.pi)
        v = (theta + np.pi/2) / np.pi

ということでUV座標の話は終わり。実際の計算を見てみます。
サンプルソースでは球体の物体を仮定しているので、球体の場合のUV座標は以下の式で計算されます。

https://en.wikipedia.org/wiki/UV_mapping#Finding_UV_on_a_sphere

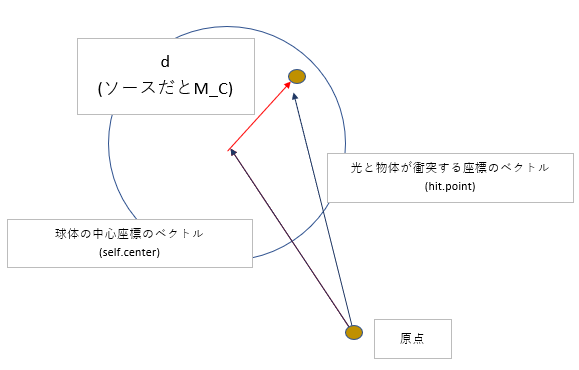
wikipediaより、球体の中心から物体表面の座標(hit)までの単位ベクトル$d$を計算し、
x成分$d_{x}$、y成分$d_{y}$、z成分$d_{z}$、より、ＵＶ座標を計算します。
サンプルソースとほぼおなじ計算ですね。（0.5は分母2$\pi$として合わせればわかる）
なお、この式は球体を前提にしていることに注意

2.UV座標とテクスチャ画像より、物体表面の座標(hit)の色を計算

UV座標とテクスチャ画像より、物体表面の座標(hit)の色を計算しましょう。
該当処理のソースは以下の通りです。

extract.py

        # 2.UV座標とテクスチャ画像より、物体表面の座標(hit)の色を計算
        # self.img はテクスチャ画像 , uvは物体表面の三次元座標に対するUV座標
        im = self.img[-((v * self.img.shape[0]).astype(int)% self.img.shape[0]) , (u   * self.img.shape[1]*self.repeat).astype(int) % self.img.shape[1]  ].T
        color = vec3(im[0],im[1],im[2])

ソースだけ見てもわかりづらいので、もう少しわかりやすく書き下します。

extract.py

        # 2.UV座標とテクスチャ画像より、物体表面の座標(hit)の色を計算
        # 画像平面x,y座標への変換
        # 画像平面x,y座標 = u,v座標 * 画像の横/縦 
        x      = v * self.img.shape[0]*self.repeat
        y      = u * self.img.shape[1]*self.repeat

        # テクスチャが繰り返されている分を考慮して、元画像の座標を修正
        x      = v_conv % self.img.shape[0]
        y      = u_conv % self.img.shape[1]
        im = self.img[-x , y ].T
        color = vec3(im[0],im[1],im[2])

０～１で正規化されているUV座標に対して、通常の画像の解像度を乗算すれば、
正規化されているので、通常の画像の全ピクセルとの対応関係がピタリと計算されて、
uv座標に対する画像の座標(x,y)が取得できます。
後は、座標(x,y)から画像のピクセルを指定することで色を取得できますね。

ソース中の「self.repeat」について触れておきます。
テクスチャ画像として１枚の画像だけを使うのであれば、ここまでの計算で画像の座標は取得できます。
しかしこのソースでは１枚のテクスチャ画像を「繰り返し」つなぎ合わせた使い方を考慮に入れています。
繰り返してつなぎ合わせることで、大きな画像を疑似的に扱うことが目的です。(↑)
こうすることで、例えば２×２のシンプルなタイルのテクスチャ画像を、広い床に展開して大きく見せたりすることができます。

2.画像の座標(x､y)より画像の色を取得

extract.py

        # 3.画像の座標(x､y)より画像の色を取得
        color = vec3(im[0],im[1],im[2])

ソースの通り、取得したピクセルのRGBをそれぞれ取得しています。

1_2.物体の法線

物体の法線もしっかり定義する必要があります。
法線というのは、表面の点に対して垂直な線のことです。
法線を可視化すると、図のように毛ガビンビンに生えたようになります。

さて、法線の必要性については、以前の記事でも少しふれました。
https://qiita.com/akaiteto/items/a687cc7e855e40d706f9
法線を定義することで、物体が反射した時にどの角度に反射するか細かく定義できるし、
拡散反射光を計算する際には、拡散する光がどの範囲で拡散するかを疑似的に計算するとき等にも役立ちます。

ゲームの３Ｄモデルは法線を一つずつ計算して手作りする場合が多いようですが、
このサンプルソースで扱うのは球体です。球体の接する法線は手作りしなくても簡単に計算できます。
ということでやってみましょう。

test.py

normal = (hit.point - self.center)  / self.radius

要するに、中心点から表面の点までのベクトルを求めればよいだけです。
球体の中心(self.center)から法線を求めたい座標(hit.point)のベクトルをもとめてやって、( = (hit.point - self.center) )
半径(self.radius)で割ってやることで単位ベクトルにします。

（※注意：これから先、単位ベクトルという単語が頻出します。
単位ベクトルとは、ベクトルの長さが「１」のベクトルです。）

2.人間の視線と物体の接点

この項では、我々がこれから創造する仮想の世界に光を与えます。
そのためのファーストステップとして行われるのが、「視線」の計算になります。

我々の世界は光が発生することで初めて物体を観測できますが、
これから創造するRayTracingの世界では、人間の視線という名の光線がまず発生します。
これがどういうことかを見ていきましょう。

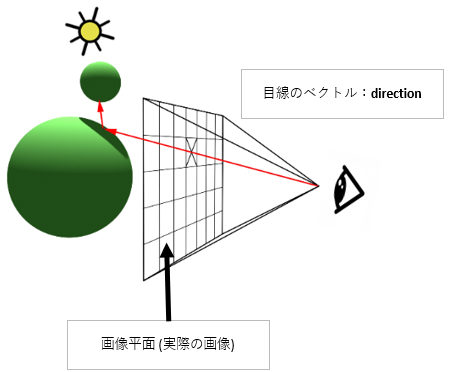
https://www.scratchapixel.com/lessons/3d-basic-rendering/introduction-to-ray-tracing/implementing-the-raytracing-algorithm

まず、RayTracingのすべては「視線」を飛ばすことから始まります。
図にグリッドの領域が描かれていますね。これが、我々の視界に映る世界を「画像平面」として表現したものです。

グリッドの領域がそのまま画像として出力されます。そのままです。
620＊420などの見慣れた画像がこの平面に描写されます。
（ピンとこないかたは、ピンホールカメラの原理を参照。焦点距離の位置に生成される実像が画像平面となります。）

そして、このグリッドの中にある×マークが重要です。×マークは、画像平面のある一つのピクセルを現します。
１．RayTracingはある一つのピクセルに対して視線という名の光線を飛ばした後、
２．物体と視線が空間上どの座標で「衝突」するかを計算します。
３．そしてそのポイントに対する反射光などの光の影響を計算し、
４．「衝突したポイントの固有色」＋「周囲の光の影響」を計算したものが、×マークのピクセルの色となります。

最終的には上記の工程をすべてのピクセルに対して行うことで、
一枚の画像、一つの視点映像が完成させます。これがRayTracingの概要となります。

2_1.衝突点

上述の通り、まずは物体と視線がどの座標で衝突するかを計算する必要があります。
そのためにもまずは視線を定式化しましょう。

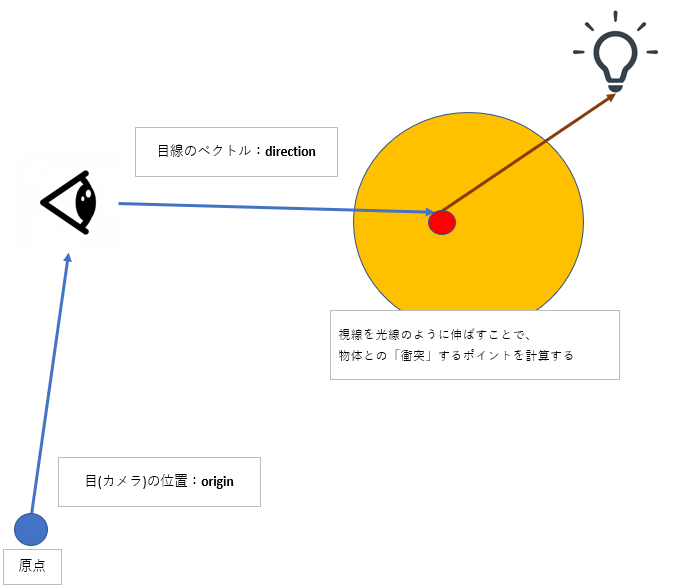
視線と物体を図にします。
求めたいものは物体との衝突点$hit.point$です。すなわち、図で言うところの青い原点から、赤い衝突点の座標（ベクトル）です。
高校数学のベクトルに従えば、下記式で表されます。

hit.point = origin + direction

視線方向のベクトル$direction$の単位ベクトルを $ray.dir$ とし、視点から衝突点までの距離を $t$ とすれば、
式は以下のようにあらわされます。

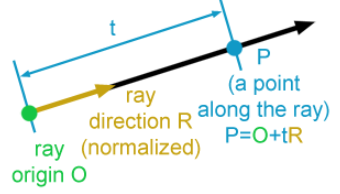
        direction = ray.dir * t より、
        hit.point = ray.origin + ray.dir * t

すなわち要約するなら、下記がわかれば、物体と視線との衝突点を計算できるようになります。
１．原点から視点までのベクトル $origin$
２．視点から衝突点までの単位ベクトル $ray.dir$
２．視点から衝突点までの距離 $t$

まずは、上記３つを求めなければいけません。
それぞれの算出については、「カメラの設定」を参照ください。

3.カメラの設定

観測者がいないと世界は何も始まりません。
ということで我々の仮想世界に観測者を置きましょう。

3_1.座標について

シミュレーションするうえで、座標を設定することは重要です。
座標ってそもそもなに？なんで重要なの？というところから整理しましょう。

さて、座標と聞くと、学校で習ったXYZの表を思い出しますね。
座標の中心を原点と呼び、原点は座標のなす空間の中心です。

それでは質問です。
座標の中心とはいったいどこにあるのでしょうか？

小学校の頃の授業だと、先生は大体黒板の真ん中にどんと矢印３つを描いていましたね。
座標の中心は黒板の真ん中にある？答えはもちろんNoです。
座標の中心は「どこにでも定義できる」というのが回答になります。

たとえば、地面から自由に防壁を張れる能力があったとしましょう。
能力者は、どの座標に防壁をはるかいちいち計算するわけですが
座標の中心をどこにおいたら計算しやすいでしょうか？

一番やりやすいのは、能力者の位置を原点に置いた場合でしょう。
能力者の目の前の方向をx方向として、左手を伸ばした向きをy方向、顔をあげる向きをz方向とすると、
能力者は直感的に位置を計算しやすいはずです。

逆に、能力者の横にいる人物を座標の中心にしたら、
隣にいる人の位置分だけ差し引いて座標を計算しないといけません。
計算は大変だし、わかりづらいですよね。

このように、座標の中心を設定するという行為は、
計算のしやすさやわかりやすさを向上させるために必要な操作になります。

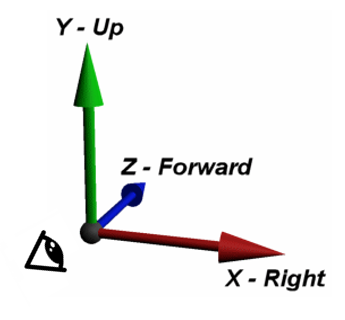
そして本稿では、原点をカメラの位置として考えます。
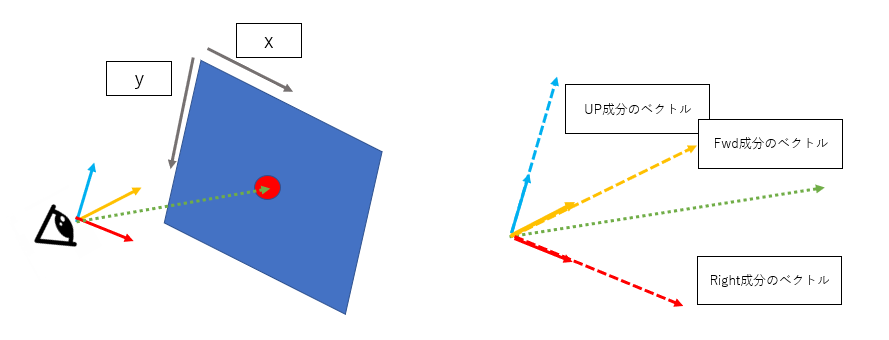
サンプルソースの中では、座標をFwd(前)、Right(右)、Up(上)として表します。
それでは、どのようにして座標系を定義するかソースで見てみましょう。

test.py

        self.cameraFwd = (look_at - look_from).normalize()
        self.cameraRight = (self.cameraFwd.cross(vec3(0.,1.,0.))).normalize()
        self.cameraUp = self.cameraRight.cross(self.cameraFwd)

上がサンプルソースの全容です。上式の計算によりFwd、Right、Upの向きや原点の位置を定義しています
もうすこし詳しく見てみましょう。

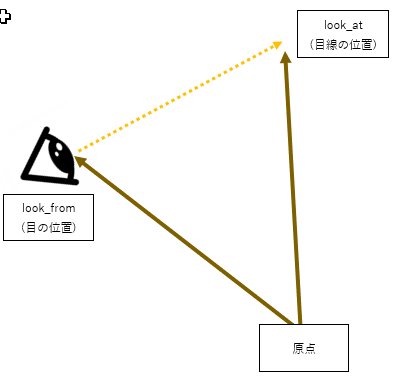
カメラを中心とした座標を計算するために、まず初めに$look from$と$look at $が入力として与えられます。
$look from$は図の通り目の位置です。原点(0,0,0)に対する(x,y,z)の座標が入っています。
$look at $は目線の先の位置です。これも同様に原点(0,0,0)に対する(x,y,z)の座標が入っています。

さて、さらりと原点が出てきました。最初の段階では、
原点を「適当な空間」に設定して、目の位置と目線の位置を定義します。

このときの原点の座標を世界座標と呼ぶ場合もあります。
そしてこれから、世界座標の世界から、Fwd/Right/Upの座標の世界に変換していくわけです。

Fwd

test.py

        #1.視線の方向を計算
        self.cameraFwd = look_at - look_from
        #2.正規化
        self.cameraFwd = self.cameraFwd.normalize()

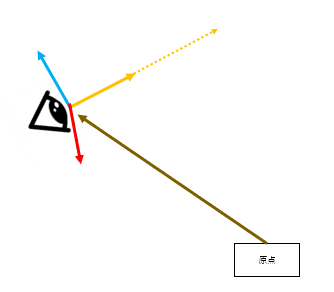
まずはFwdの計算。処理を分解してみました。
「1.視線の方向を計算」では、
　　$look from$と$look at$をそれぞれベクトルとみなして、
　　黄色い点線の視線ベクトル$direction $を計算します。
「2.正規化」では、
　　求めたベクトルに長さがあると
　　デカルト座標のx,y,zのような扱いやすい基底にしづらいので
　　扱いやすくするために長さ１の単位ベクトルにします。

Right , Up

test.py

        self.cameraFwd = (look_at - look_from).normalize()
        self.cameraRight = (self.cameraFwd.cross(vec3(0.,1.,0.))).normalize()
        self.cameraUp = self.cameraRight.cross(self.cameraFwd)

あとは、Fwdに対して基底の定義に当てはまるように、
Fwd、right,upすべてが直角の関係で、長さが１になるように直積でRightとUpを求めます。
直角のベクトルを求めたいときは直積です。

3_2.視線位置（origin）の計算

目の位置なので、$lookfrom$をそのまま返します。

3_2.視線方向（ray.dir）の計算

ソースを抜粋します。

test.py

        ray.dir = (self.look_from  +   self.cameraUp*y*self.focal_distance  +  self.cameraRight*x*self.focal_distance  + self.cameraFwd*self.focal_distance  - look_from).normalize()

単純化すると、

test.py

        direction = self.look_from  +   self.cameraUp*y*self.focal_distance  +  self.cameraRight*x*self.focal_distance  + self.cameraFwd*self.focal_distance
        ray.dir = (direction  - look_from).normalize()

「2_1.衝突点」と同じような式ですね。.normalize()によって、視線方向は単位ベクトルに変換されます。
問題は$#direction$です。さらに分解してみます。

test.py

        視線の位置 = self.look_from  
        UP成分のベクトル = self.cameraUp*y*self.focal_distance
        Right成分のベクトル = self.cameraRight*x*self.focal_distance
        Fwd成分のベクトル =self.cameraFwd*self.focal_distance
        direction = 視線の位置 + UP成分のベクトル +Right成分のベクトル + Fwd成分のベクトル

あらためて説明すると、$direction$は図の赤い矢印のベクトルです。
正確に言えば、目から画像平面までのベクトルになります。
目から画像平面までの距離は「self.focal_distance」で表されます。
「x」「y」は画像平面上の座標、つまりピクセルの座標です。

これをソースに合わせて図解すれば、
視線方向$direction$は、焦点距離と画像のピクセル座標(x,y)より、
Fwd/UP/Right成分のそれぞれのベクトルを計算し、それらを合算することで計算されます。
そして、計算した後、視線の位置である「self.look_from 」を足し合わせることで、世界座標に戻します。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

これから更に流行るであろうフォトリアルな世界について勉強しよう 物体とカメラの設定編

ここまでの流れ

RayTracing

目次

今回やること

1.物体の設定

1_1.物体の形状

1_1.物体の色

（１）物体が単色の場合

（２）物体がテクスチャの場合

1.物体表面の座標(hit)から、UV座標を計算

2.UV座標とテクスチャ画像より、物体表面の座標(hit)の色を計算

2.画像の座標(x､y)より画像の色を取得

1_2.物体の法線

2.人間の視線と物体の接点

2_1.衝突点

3.カメラの設定

3_1.座標について

Fwd

Right , Up

3_2.視線位置（origin）の計算

3_2.視線方向（ray.dir）の計算

これから更に流行るであろうフォトリアルな世界について勉強しよう　物体とカメラの設定編