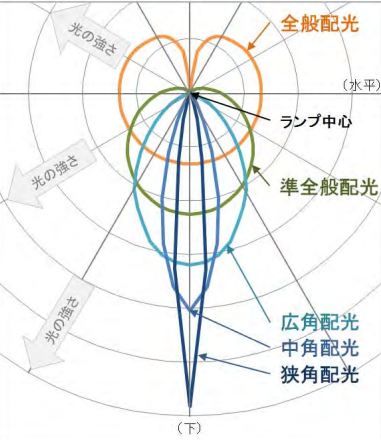
去年Googleが発表した「Total Relighting」
一枚の画像から、人物を切り出し、背景に合わせて人物のライティングを自動で調整する手法。
・・・らしいのですが。すごいですよね。
フォトリアルというと、最近は3D分野の目覚ましい発展を連想しますが、
3Dはどうしても装置や機材に依存するイメージが付きまといます。
もしもiphoneなどの単眼カメラで実現できるようになれば、
表現の世界はさらに次のステージに進めそうです。
ということで今回はそんな「フォトリアル」な世界について勉強します。
できるだけ数式と実際のソースに基づいて理解を深めていきます。(目標)
参考:
https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-overview/light-transport-ray-tracing-whitted
https://msyksphinz.hatenablog.com/entry/2020/06/26/040000
http://webcache.googleusercontent.com/search?q=cache:qdi9_qbsG0QJ:kanamori.cs.tsukuba.ac.jp/jikken/inner/reflection_refraction.pdf+&cd=2&hl=ja&ct=clnk&gl=jp
https://www.cs.utexas.edu/users/fussell/courses/cs384g-fall2011/lectures/lecture11-Drt.pdf
https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-generating-camera-rays
ここまでの流れ
- 1.概要編
- 「こんなことやるんだー」という概要
- 2.RayTracing詳細編
RayTracing
RayTracingってなに?
RayTracingは光と物体の関係をシミュレーションすることで、リアルな世界を疑似的に再現する手法の一つです。
この記事では、RayTracingの一連の流れを踏まえたうえでの具体的な計算方法を勉強します。
https://github.com/rafael-fuente/Python-Raytracer

数式ばかりだと実勢に組む時にイメージがつかないので、上記のソースをベースに勉強します。
「Python-Raytracer」というプロジェクトは、RayTracingを実装したソースです。(私の作ったものではありません)
外部のライブラリに頼らず全部一から作成しているので、環境構築がものすごく楽で勉強におすすめです。すごい。
pip install pillow
pip install numpy
↑上記のライブラリがpythonの環境に入っいて、python3.6i以上なら基本的に動くと思います。
本記事では、「Python-Raytracer」のexample.pyを下記のように書き換えて、
拡散反射がどのような計算のもとでRayTracingされるかを見てみます。
from sightpy import *
# https://github.com/rafael-fuente/Python-Raytracer
# 物体の設定
diff_material =Diffuse(diff_color = rgb(0.9, 0, 0.1),diffuse_rays = 40)
# 背景色の設定
Sc = Scene(ambient_color = rgb(0.05, 0.05, 0.05))
# カメラの設定
angle = -np.pi/2 * 0.3
Sc.add_Camera(look_from = vec3(2.5*np.sin(angle), 0.25, 2.5*np.cos(angle) -1.5 ),
look_at = vec3(0., 0.25, -3.),
screen_width = 400 ,
screen_height = 300)
# 光の設定
Sc.add_DirectionalLight(Ldir = vec3(0.52,0.45, -0.5), color = rgb(0.15, 0.15, 0.15))
Sc.add(Sphere(material = diff_material, center = vec3(-.75, .1, -3.),radius = .6, max_ray_depth = 3))
# 背景画像の設定
Sc.add_Background("stormydays.png")
# レンダリング実行
img = Sc.render(samples_per_pixel = 6)
img.save("EXAMPLE1.png")
img.show()
目次
RayTracingで光をシミュレーションするには、様々な「定義」が必要です。
聖書の中の神様は、まず「光」の存在を定義したように、
我々も必要なものを一つずつ「定義」をしないといけません。
例えば、
- 物体の色は何色なの?
- 目(カメラ)は空間のどこに位置しているの?
- 目(カメラ)に物体は映るの?
- 光はどう反射するの?
などですね。
これらを定義する工程を以下の目次に書き出しました。
本稿では、定義方法や計算方法を一つずつ整理しながら、
最終的にどのようにシミュレーションを行うかを見ていきます。
- 1.物体の設定
- 1_1.物体の形状
- 1_2.物体の色
- (1)物体が単色の場合
- 単色の色を設定
- (2)物体がテクスチャの場合
- テクスチャのUV座標・物体の3D座標より色を取得
- (1)物体が単色の場合
- 1_3.物体の法線
- 2.人間の視線と物体の衝突点
- 2_1.衝突点
- 3.カメラの設定
- 3_1.座標について
- 3_2.視線位置(origin)の計算
- 3_2.視線方向(ray.dir)の計算
- 4.光の設定
- 5.反射光の設定
- 5_1.拡散反射光
- 5_1_1. 接点の未加工の色の設定
- 5_1_2. 拡散反射の設定
- 拡散反射光のベース色の設定
- 拡散反射光の本数の設定
- 拡散反射光の分布の設定
- 拡散反射光の強さの設定
- 5_1_3. 最終的な色の計算
- 5_1.拡散反射光
今回やること
今回は
5.反射光の設定
を行います。
5.反射光の設定
反射する光の設定を行いましょう。
https://qiita.com/akaiteto/items/a687cc7e855e40d706f9
以前の記事で、反射光の種類について触れました。
理想的につるつるした素材なら「正反射」するし、
表面がざらざらした物体なら、「正反射成分」を伴って正反射し、
物体内部に侵入した光が再び表面から放出される「拡散反射光」も伴うと勉強しました。
本稿では、拡散反射光を例に、光をどのように設定して計算するか見てみましょう。
5_1.拡散反射光
拡散反射光を設定するうえで、定義しないといけないものを一つずつ整理します。
5_1_1. 接点の未加工の色の設定
まずは色です。ここで言う色とは物体の色。
これは以前の記事の復習ですね。
(https://qiita.com/akaiteto/items/dc829bb92e52471c5afa)
同記事の「2.人間の視線と物体の接点」より、視界に映る物体のポイントの座標を取得した後、
同記事の「1.物体の色」より、座標の示す物体の色を取得します。
ここまでの操作で未加工の色が手に入りました。
そしてこれからの処理が本稿の内容。
取得した物体の色に対して、拡散反射光がもたらす色の変化分を計算することで色を再現していきます。
5_1_2. 拡散反射の設定
拡散反射光のベース色の設定
拡散反射光の設定において必要なもの。まず1つ目は拡散反射光の「色」です。
この世界の光には必ず色があります。蛍光灯なら緑に近い色、LEDなら白色だけど少し青みがかったような色です。
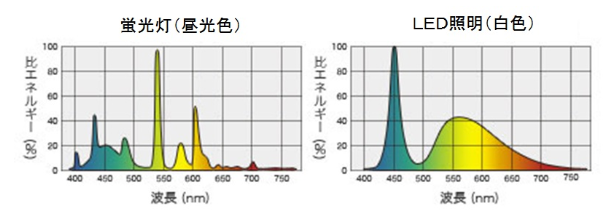
さて、拡散反射光の色とはどんな色でしょう?
拡散反射光は、内部から漏れ出すように反射した光です。
なので、内部から漏れ出す光は物体内部の影響を受けて物体の「固有色」が光の色に現れます。
例えば人間であれば、内部の血の「赤色」が拡散反射として現れます。
diff_material =Diffuse(diff_color = rgb(0.9, 0, 0.1),diffuse_rays = 40)
ソースでは、255で正規化した数値でrgb(0.9, 0, 0.1)と固定の色で指定しています。
拡散反射光の本数の設定
現実世界に於ける光は、粒子でもあり波でもあります。
直進する一本の線として光を定義するなんてきいたら、もしかしたらアインシュタインが異を唱えるかもしれませんね。
ただ、仮想世界においては光を一本の光線と捉えたほうが計算しやすいので、光線として考えます。
本数は図で言うところの赤い線です。
普通光はこんな線で見えませんが、仮想的に線とみなします。
diff_material =Diffuse(diff_color = rgb(0.9, 0, 0.1),diffuse_rays = 40)
ソースでは$diffuse rays$に40本と指定します。
拡散反射光の分布の設定
ここまでの定義が拡散反射光の基本的な性質。
この項では、もっとも重要な「分布」について記載します。
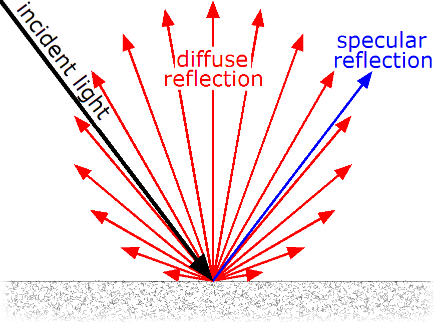
この図をみると、拡散反射光はキレイな円を描くように反射していますね。
現実世界において、すべての物体がこのようにキレイに反射するかといえば、答えはNOです。
以前、拡散反射光は内部から放出される光だと言いました。
その実態は、物体内部の様々な構成物に光が反射することで光が様々な方向に飛び出すのです。
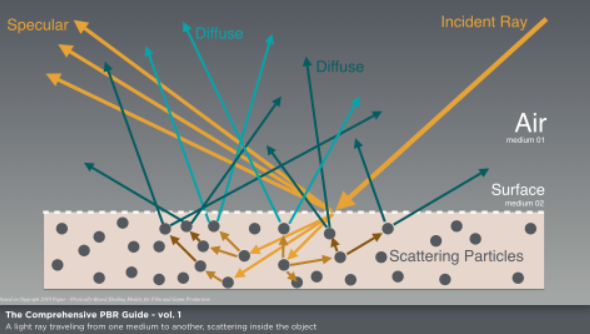
物体内部の構成物は物体によって様々です。
例えば人間であれば、拡散反射光は血を反射した光、すなわちヘモグロビン一粒一粒を反射した光なわけですが、
同じ人間だからといって、ヘモグロビンの分布や数が同じではありません。
血の気の少ない御老人は拡散反射が減って白っぽくなるし、
血流が活発な子供は拡散反射がおおくてほっぺたが赤っぽい。
人間によって拡散反射の分布は多種多様になります。
「拡散反射光をどのように分布させるか。」
現実世界に忠実に再現しようとしたときの、一つの課題と言えるでしょう。
法線マップによって、物体の凸凹を一つずつ定義することは手作りで可能だったとしても、
拡散反射光を生み出す内部の構造を定義して、拡散特性を自作するのは並大抵のことではありません。
とある研究では、人間それぞれの拡散特性を計測するために、
大掛かりな回転式の球体の照明を作成して測定した研究もあるくらいです。
https://www.pauldebevec.com/Research/LS/debevec-siggraph2000-high.pdf

仮想世界において、この拡散特性を完全に再現することは非現実的。
擬似的に分布を作成することが、現実的なアイティアです。
順全般配光
とりあえずは、一般的な光の分布を擬似的に適用させてみましょう。
ということで世の中にたくさんあるライトの分布を見てみます。
複雑な形の配光がたくさんある中、「順全般配光」が一番とっつきやすい円の形をしていますね。
円形に光が分布する想定のもと、計算してみましょう。
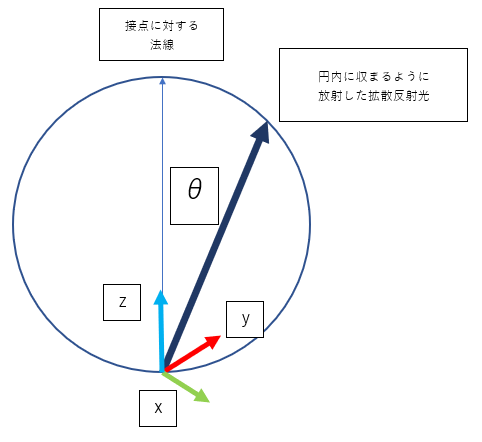
光は接点を中心に円を描くように分布すると仮定します。
分布を求めるために必要なものは、「円の中でどのように矢印が飛び交うか」です。
すなわち、スカラーではなくベクトル。矢印がどの向きにどの長さで飛び交うかを計算します。
ということで、
1.接点を中心とした座標系の基底ベクトルを計算
2.1の座標系のXYZ軸それぞれの成分を計算
3.2の成分を合算して世界座標のベクトルを作成
という流れでベクトルを計算しましょう。
1.接点を中心とした座標系の基底ベクトルを計算

座標という概念について、整理します。
この仮想世界は、適当な位置に設置された「原点」を中心とした世界座標で構築されています。
物体や視線の位置はすべて世界座標で定義されています。
そして今回、計算したいのはある物体の表面の点を中心とした計算なのですが、
いちいちはるか遠くの原点を考慮して計算したらが少し直感的じゃなくわかりづらいですよね。
ということで、計算を可視化しやすくするように、新たな座標の設定を行いましょう。
座標の中心を都合の良い場所に移動させます。今回で言えば、接点を中心に新たな座標系を作りましょう。
ax_z = n
ax_x = ax_z.cross(ax_z).normalize()
ax_y = ax_z.cross(ax_x)

https://qiita.com/akaiteto/items/dc829bb92e52471c5afa
以前の記事、「カメラの設定」の項でやったときと同じような計算です。
まずは、接点を中心としたときのXYZ軸の基底(↑図xyzのところ)を計算します。
ソースのcrossという関数は直積。直積を計算すれば垂直のベクトルが計算されるので、
法線ベクトルを中心に直積を計算することで、法線ベクトルを中心としたx,y,z軸の基底が計算されます。
2.1の座標系のXYZ軸それぞれの成分を計算
# r2 : 「円内に収まるように放射した拡散反射光」の長さ
# theta: 法線と拡散反射光のなす角度
Z軸の長さ = np.abs(n) # = 1 (単位ベクトルなので1)
z成分 = r2
x成分 = np.cos(theta) * r2
# y成分 = np.cos(np.pi/2 - theta) * r2
# cos(np.pi/2 - theta) = sin(theta)より下記式
y成分 = np.sin(theta) * r2
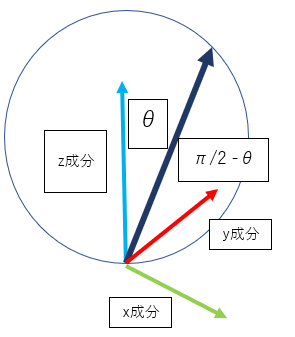
「円内に収まるように放射した拡散反射光」の長さを$r2$、
法線と拡散反射光のなす角度を$\theta$とします。
高校数学のsincosの関係で拡散反射光のXYZ成分を計算します。
ここで求めた成分はこの座標系における座標であり、(x,y,z) = (1,2,3)のような座標が計算されています。
ここまでの計算により、接点を中心としたときの座標を計算することができました。
3.2の成分を合算して世界座標のベクトルを作成
return ax_x*x成分 + ax_y*y成分 + ax_z*z成分

接点を中心としたときの座標を世界座標の原点の世界に戻します。
基底×成分の大きさを計算して合算することで、世界座標系におけるベクトルが計算されます。
以上の計算により、世界座標における拡散反射光の分布ベクトルが求められました。
ランダム要素について:モンテカルロ法
# r2 : 「円内に収まるように放射した拡散反射光」の長さ
# theta: 法線と拡散反射光のなす角度
さて、ここまでの計算は
・分布する拡散反射の「長さ」と
・法線と拡散反射光のなす「角度」を
既知のものとして扱いました。
角度と長さを固定しているので一本の分布ベクトルしか計算できません。
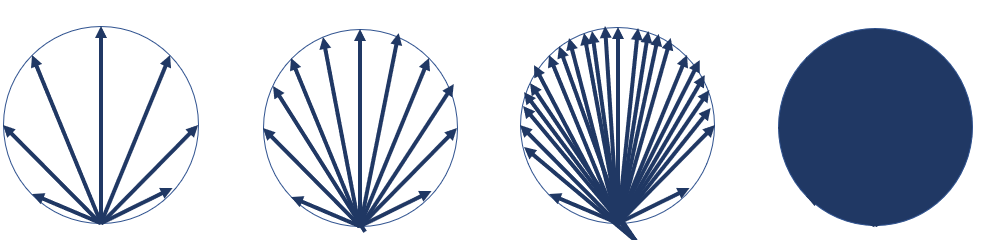
最終的にシミュレートしないといけない拡散反射光の分布は、
何本も何本も光が拡散して、矢印で埋め尽くされるくらいに分布していないといけません。
これを安直に実現しようとしたとき、
例えば、角度を0.000001ずつ変えて矢印を計算すれば実現できるかもしれませんが、途方もない計算がかかりそうです。
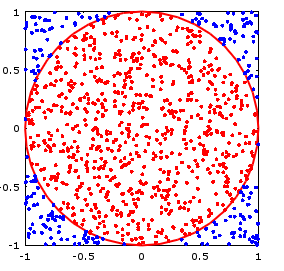
https://www.timedia.co.jp/tech/octave/
ということで、こんなときに実行するのがモンテカルロ。
モンテカルロによって、丸い円内に発生する拡散反射の分布を再現します。
念のため、モンテカルロを知らない方向けに簡単に説明します。
例えばここに、サイコロがあるとします。
その人は目隠しされていて、このサイコロは一体何面あるかわかりません。
そのダイスは普通の6面かもしれないし、TRPG用の20面かもしれません。
手元にあるダイスが一体何面なのかを知ろうと思ったら
とにかくダイスを振りまくるのです。そして、ダイスの目を記録し続けます。
何度も何度も「ランダム」に振り続ければ、1~20の目は何回もデてくるのに対して、
それ以上の目は全く出てこないことでしょう。
この一連の操作により、目隠しされた人はダイスが「20面」であることに気づくのです。
すなわち、ランダムに試行を繰り返すことで擬似的に求めるのがモンテカルロと名のつく手法になります。
要するに、角度と長さランダムな数値でたくさん計算することで、
拡散反射光の矢印がびっしり埋まった状態を再現しようというわけです。
それでは、角度と長さのランダムに値を決めるときの範囲について考えましょう。
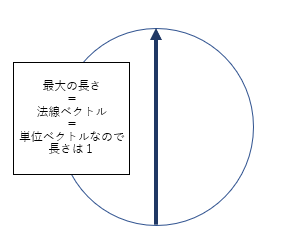
分布する拡散反射の長さは、最小は0、最大は1です。
最大が1の理由は、これまで図にしてきた円は、法線ベクトルを直径とする円のためです。
法線ベクトルは全て単位ベクトルで表されるため、長さは1が最大になります。
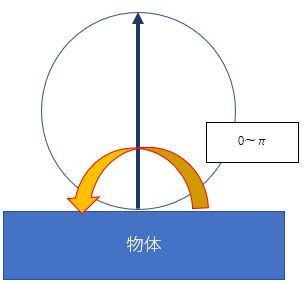
法線と拡散反射光のなす角度は0~180度です。
上記の範囲で角度と長さをランダムに発生させ、冒頭で定義した「40本」の拡散反射光の分布を計算します。
拡散反射光の強さの計算
拡散反射光がどの方向に進むかの向きは計算できてたの、次は光としての強さを計算しましょう。
光の強さを表す概念は色々あるわけですが、放射照度、放射輝度の概念についてふれつつ
最終的に放射輝度で光の強さを計算します。
放射照度
E = \frac{d\phi}{dS}
放射照度は、微小面積$dS$あたりの放射束$d\phi$と定義されます。
E = \frac{\phi}{S}
面積$S$あたりに放射束$\phi$が放射されるなら割り算すれば求められます。
分母に面積がいるので、面積が大きくなればなるほど放射照度は反比例して弱まります。
そして、このときの放射照度$E$を面に対して垂直に照射しているとみなしたとき、
法線に対して$\theta_{i}$で斜めに光が照射されているとすれば、
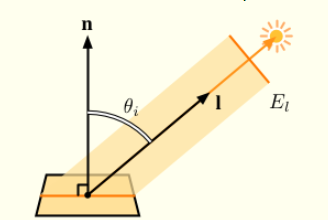
https://marina.sys.wakayama-u.ac.jp/~tokoi/?date=20150826
放射照度$E_{l}$は下記式で表されます。
E_{l} = Ecos\theta_{l}
ということで、今回の例にこれを当てはめれば、

入射光の放射照度を$E$とすれば、拡散反射光の放射照度は$Ecos\theta$で求まることがわかります。
放射輝度
放射照度は光が入射したときの計算です。逆に放射輝度は光が反射するときの計算となります。
放射輝度の説明の前に立体角という概念の整理をします。
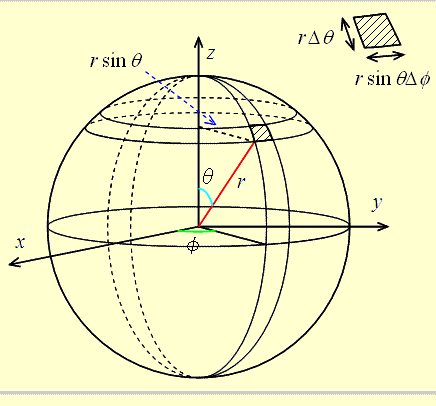
http://www.iwata-system-support.com/CAE_HomePage/vector/differential17/differential17.html
立体角(Solid Angle)とは、図のように$\theta$,$\phi$の角度を導入することで、
錐体(円錐みたいなやる)で区切られた部分を表現したものになります。
このとき、$\theta$,$\phi$をなす錐体の球体表面の面積は下記式で表されます。
dA = r^{2}sin\theta d\theta d\phi\\
単位円なので、r = 1より\\
dA = sin\theta d\theta d\phi
さて、放射輝度の話に戻りましょう。
放射照度では微小面積$dS$に対する放射束を計算しました。
そして放射輝度とは、光が照射される面積を微小立体角(Solid Angle)とみなしたときの放射照度となります。
つまり放射輝度は、$dA$を照らした領域に対する放射照度といえます。
立体角のなす微小面積$dA$についてもう少し掘り下げます。
微小面積$dA$は、球面にそっているので入射角度に対して斜めになっています。
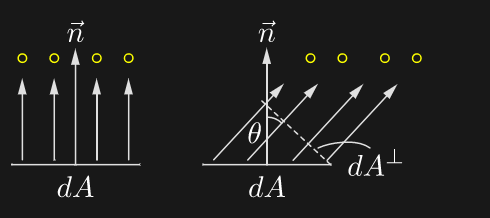
ソースでは、光の進行方向に対して垂直になるように面の面積を調整します。
すなわち、$cos\theta$を掛け合わせることで、いわゆる投影面積を取得します。
dA = cos\theta sin\theta d\theta d\phi
上記の微小面積より、実際の面積を計算しましょう。
$\theta$、$\phi$の範囲を決めて実際の面積を求めます。
面積 = \int_{A}cos\theta sin\theta d\theta d\phi\\
面積 = \int^{2\pi}_{0}\int^{pi/2}_{0}cos\theta sin\theta d\theta d\phi\\
面積 = \pi
ということで、求めたい放射輝度$L$は下記式となります。
拡散反射光の照度$Ecos\theta$より、
L_{diffuse} = \frac{1}{面積}(拡散反射光の照度)\\
L_{diffuse} = \frac{1}{\pi}Ecos\theta
内積の公式より、$cos\theta$を法線ベクトル$n$と拡散反射光の単位ベクトル$diffuse_dir$で表すと、
L_{diffuse} = \frac{1}{\pi}diffuse dir \cdot n
これが拡散反射光の輝度になります。では実際のソースを見てみます。
np.clip(ray_dir.dot(self.normal),0.,1.)/np.pi
np.clipは、0以下は全て0、1以上は全て1になるように調整されていますが、
それ以外は同じことがわかります。
5_1_3. 最終的な色の計算
光の計算の復習
復習です。
https://qiita.com/akaiteto/items/a687cc7e855e40d706f9
入射光の光の強さを表す輝度を計算するとき、この記事ではランバートモデルを仮定することで光を計算しましたね。
BRDF(\theta_{in},\phi_{in},\theta_{out},\phi_{out}) = \frac{L_{out}}{E_{in}}\\
\frac{L_{out}}{E_{in}} = \frac{\varrho_{d}}{\pi}\\
L_{out}=\frac{\varrho_{d}}{\pi}E_{in}
ランバートの意味するところはつまり、
入射(in)反射(out)に対する光量$\phi$の大きさに関わらず、入射する光と反射する光の強さの比率は
すべて$\frac{\varrho_{d}}{\pi}$で表され、アルベド${\varrho_{d}}$が一定とすれば入射と反射の割合は常に一定。
言い換えれば、拡散反射光のあの様々な矢印の反射光はどれもすべて同じ強さだと仮定しています。
L_{out}=\frac{\varrho_{d}}{\pi}\phi_{in}n\cdot s
そして上式。上式は、反射光は$cos\theta$に比例する性質と、
入射した光の単位ベクトル$s$と法線ベクトル$n$の内積の公式より導かれます。
復習終わり。
ランバートに基づく輝度の計算
色を求める前に輝度を求めましょう。
輝度$L_{in}$とは光の強さ、直感的に言えばこの値によって明るさが決まるわけです。
L_{in}=\frac{\varrho_{d}}{\pi}\phi_{in}n\cdot s
この式からさらに、レイトレーシング向けに式を変形させます。
まず、放射束$\phi_{in}$は入射光の強さを表したものです。
これまでの計算では光の最小単位として一本の線で光を表してきたわけですが、この一筋の光の大きさを「1」と仮定しましょう。
L_{in}=\frac{\varrho_{d}}{\pi}n\cdot s
続けて、アルベドを式にしましょう。
\varrho_{d} = \frac{Light_{out}}{Light_{in}}
拡散反射光の場合、入射光が$Light_{in}$、拡散反射が$Light_{out}$となります。
アルベド$\varrho_{d}$。しれっと使ってきた言葉ですが、アルベドの補足をします。

光が物体に入射したとき、光のいくつかは物体をすり抜けたり、吸収されてしまうこともあります。
なので、反射した光は入社した光よりも弱くなります。入射光と反射光の光の強さの比率を表したものがアルベドと呼ばれるものです。
ということで、先程の輝度を展開します。
L_{in}=\frac{\frac{Light_{out}}{Light_{in}}}{\pi}n\cdot s
よって、輝度$L_{in}$を求めるのに必要なものは、下記のとおりです。
・1.アルベドの計算 - 光の強さ$Light_{out/in}$
・2.法線ベクトルの単位ベクトル$n$
・3.入射光の向きの単位ベクトル$s$
これらがわかれば、ひとまず輝度がわかるようになります。
1.アルベドの計算
\varrho_{d} = \frac{Light_{out}}{Light_{in}}
入射光$Light_{in}$、拡散反射が$Light_{out}$を考えましょう。
拡散反射$Light_{out}$は、「拡散反射光の強さの計算」で説明したとおりです。
入射光$Light_{in}$はなんでしょうか。ソースを見てみます。
color_temp = get_raycolor(Ray(nudged_repeated, ray_dir, ray.depth + 1, n_repeated, ray.reflections + 1, ray.transmissions, ray.diffuse_reflections + 1), scene)
ソースだけだとわかりづらいのですが、
ここでは、拡散反射光で行ってきた輝度の計算を再帰的に行っています。
つまり、入射される光そのものも、どこかからの反射光だという考えのもと計算が行われます。
入社される光は最終的に、「4.光の設定」で指定される光源の光が指定されます。
2.法線ベクトルの単位ベクトル
以前の記事の「1,物体の設定」にて設定した法線になります。
https://qiita.com/akaiteto/items/dc829bb92e52471c5afa
今回は球体なので、球体の中心から表面の座標までのベクトルになります。
3.入射光の向きの単位ベクトル$s$
「拡散反射光の分布の設定」にて設定した拡散反射光の分布のベクトルになります。
4.最終的な輝度
L_{in}=\frac{\frac{Light_{out}}{Light_{in}}}{\pi}n\cdot s
この部分をソースでは以下のように計算します。
(Light_In / Light_out) * NdotL / (np.pi)
5.輝度を色に反映
ここまでの計算で、ピクセルの輝度、すなわち明るさは決まりました。
これをRGBの色にどう反映させるかが次の問題です。
まず色空間というものについて整理します。
私たちはRGBという色空間をよく使います。赤青緑を0~255の範囲で指定するものです。
例えば仮に、求めた輝度をRGBそれぞれにかけ合わせたとしても、
色はくらくならないでしょう。
輝度と相性のいい色空間で計算する必要があります。
例えば、HLSという色空間であれば、色相・彩度・輝度で色を構成するので、
HLSの輝度なら相性が良いのかもしれない。
が、一般的なやり方としては「リニアRGB」という色空間で計算を行います。
https://discuss.pixls.us/t/what-does-linear-rgb-mean/16584/6
rgb_linear = np.where( rgb <= 0.03928, rgb / 12.92, np.power((rgb + 0.055) / 1.055, 2.4))
ソースでは正規化された通常のRGBを上記のように変換しています。
リニアRGBは輝度に対して比例する性質をもつらしく、
リニアRGBの値にそのまま輝度を掛け合わせることで色に輝度を反映させることができます。
color += diff_color * color_temp.reshape(N.shape()[0], self.diffuse_rays).mean(axis = 1)
ソースの該当部分は上記です。
「diff_color 」は物体の未加工の色になります。
これに対して掛け算している部分が輝度です。
ぱっと見わかりづらいですが、
1つの接点に対して40本分の拡散反射の輝度を平均化させたものをかけ合わせています。
おわり