直感でわかる、ヒューリスティック問題の羅針盤 ～貪欲法から山登り法まで～

こんにちは、square1001 です。

本記事では、いろいろな最適化問題でできるだけ良い答えを効率的に出す「ヒューリスティクス」について紹介します。また、ヒューリスティックの代表的な手法である貪欲法と山登り法について解説し、このような問題の解き方にはどのような世界が広がっているのかを感じさせることを目標としています。

ですので、アルゴリズムに興味のある方や実務で最適化問題に取り組んでいる方はもちろん、最近話題の AtCoder Heuristic Contest (AHC) に入門したい方にもおすすめです。

おことわり

本記事は、2022 年 3 月 20 日に JOIG 2021 春合宿 で講義した内容を少しアップグレードし、記事化したものになっています。

40～70 分程度で読むことを想定しています。前提知識はあまりなく、プログラミングをやっていれば記事の内容の多くは理解できると思います。また、効果的に読むために、今のうちに紙と鉛筆を手元に用意しておくことをおすすめします。

目次

章	タイトル	備考
1	はじめに	ヒューリスティクスの世界を概観します
2	問題の取り組み方	パズルをもとに、このような問題の取り組み方を教えます
3	貪欲法	「貪欲法」という手法について説明します
4	山登り法	「山登り法」という手法について説明します
5	おわりに

1. はじめに

最初に、本記事ではどのようなトピックを扱うのかについて、少し説明したいと思います。

1-1. 本記事で扱うトピック

21 世紀になり、IT 化が急速に進む今、現実社会ではいろいろなものが最適化されて動いています。これを形作るプログラミングの現場でも、例えば以下のような問題を考えたり、あるいは実際に使ったりすることもあるのではないでしょうか¹。いくつか例を挙げてみましょう。

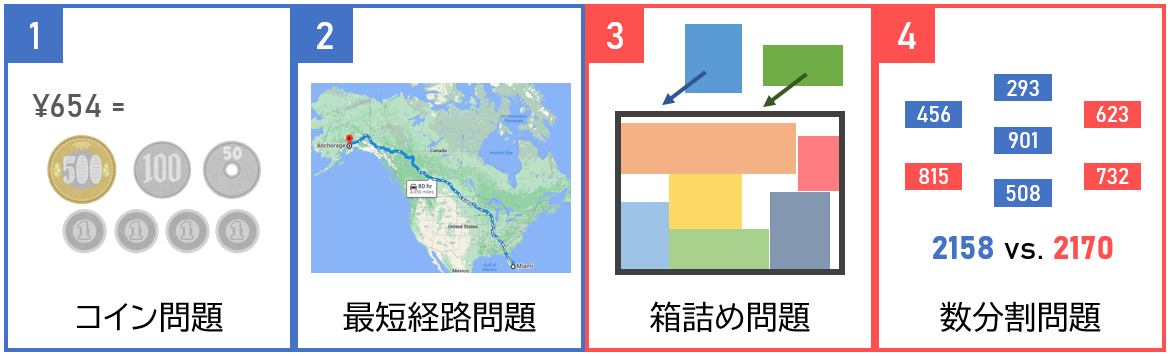
• 例 1. コイン問題：特定の金額をぴったり支払うために、最小で何枚の硬貨が必要か？
• 例 2. 最短経路問題：地図上の A 地点から B 地点までに行くのに、最短で何メートル歩く必要があるか？
• 例 3. 箱詰め問題：長方形の箱に、できるだけ多くの荷物を敷き詰めたい
• 例 4. 数分割問題：「できるだけ合計の値が近くなるように」2 つのグループに分割したい

このように、いろいろな問題があります（もちろん名前を覚える必要はありませんが）。

まず、例 1 の「コイン問題」は簡単に解けます²。みなさんも日常生活でやっているように、大きい硬貨から順に支払っていけば、最小枚数になります。また、例 2 の「最短経路問題」も、ダイクストラ法 という方法を使って高速に最適解を出すことができます。

一方、例 3「箱詰め問題」、例 4「数分割問題」のように、解くことが難しい問題もあります。例えば「数分割問題」は、データの数が 20 個程度なら分割の方法を 2²⁰ 通り全探索できますが、データの数が 100 個や 200 個になれば、コンピューターの計算速度をしても最適解を出すのは難しいです。

実際には「コイン問題」や「最短経路問題」のような "都合のよい" 問題のほうが少なく、多くの問題は解くことが難しいです。このような問題は、データの数が少し増えただけで一気に計算量が増え、コンピューターの力では最適解が出せなくなります。仮に全部の問題が解けてしまったら、世界に悩みの種は完全に消えてしまい、現実と矛盾してしまうので当然です³。

では、このような問題はどのように取り組めばよいのでしょうか？

実は、最適解を出すことはできなくても、本記事で紹介するような技法を使いこなせば、多くの問題で「平均的にかなり良い答え」を出すことができます。このアプローチを ヒューリスティクス (Heuristics) といいます。

1-2. アルゴリズムの力で解く 3 つの問題例

さて、アルゴリズムの技術を使えばどんなレベルのことができるのか見るために、ここでは 4 つの問題を紹介したいと思います。

問題例 1

平面上にチェックポイントが $N$ 個あります（これらの座標が入力されると考えてください）。すべてのチェックポイントを $1$ 度ずつ通る経路は、$N-2$ 回曲がる折れ線のようになりますが、その折れ線で最も小さい角度を スコア とします。あまり急に曲がりたくないので、このスコアをできるだけ大きくすることを考えてみましょう。

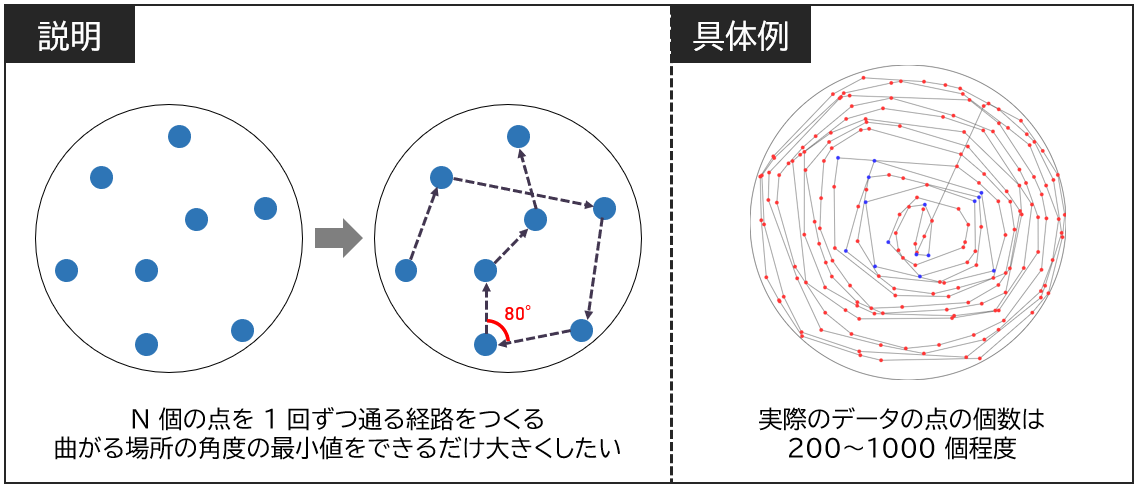
もちろん、チェックポイントの個数が 10 個程度なら経路を全通り試すことができますが、1000 個にもなればこの方法は絶望的です。また、上図の一番右の例のように、外側から巻いていくように経路を作っても、真ん中の部分でどうしても角度が小さくなってしまうので、スコアは低くなってしまいます。

しかし、アルゴリズムの力は素晴らしく、本記事で説明する「山登り法」などの手法を使えば、実はかなり良い解を短時間で出すことができます。さらに工夫すると、チェックポイントの個数が 1000 個程度でも、すべての角を 150° 以上にする魔法のような経路を求めることさえできてしまいます。

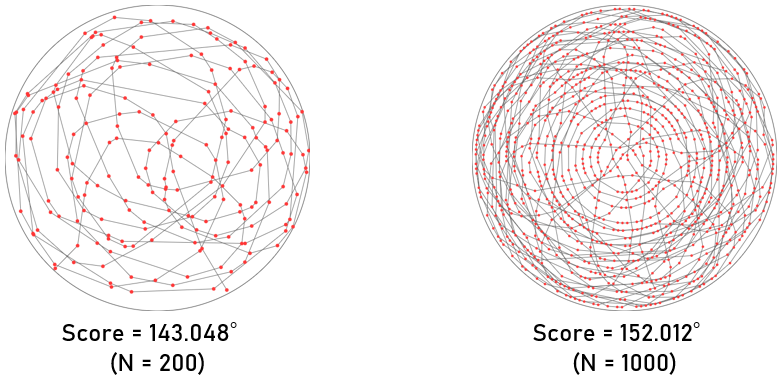
意外なことに、経路は複雑にからみ合っていますが、どの点を見ても角度が大きいことが分かるでしょう。多くの方が想像するような "ルールベースの" 方法ではもはや作りようがありませんが、この記事を読めば「こんなのどうやって作るのか？」のイメージがほんの少しでもつくかもしれません。

（この問題は情報オリンピックで過去に出題された「曲芸飛行」という問題です。もし解きたければ AtCoder 上で解くこともできます。問題文は こちら で、ジャッジのリンクは こちら です）

問題例 2

ひとつの半径 1 の円に、等しい半径の小さな円を 100 個敷き詰めることを考えます。その 100 個の円の半径をどこまで大きくできるでしょうか？

この問題はよく知られた問題ですが、最適解を求めるのは決して簡単ではなく、円が 100 個の場合の最適解はまだ知られていません⁴。

しかし、最適解にとても近い答えなら求められます。現在知られている最良の解は、下図のような半径が約 0.090235 の配置になっています。

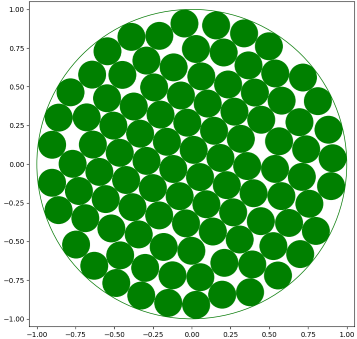
これを見ると規則性などどこにも見当たりませんが、現代のアルゴリズム技術を使いこなせば、このような配置を見つけることさえできてしまいます。

問題例 3

ところで、みなさんはテトリスで遊んだことはありますか？テトリスは、落ちてくる小さなブロックを積み上げるゲームです。一段が全部ブロックで埋まるとその列が消されるので、盤面からあふれないように上手くブロックをはめる必要があります。

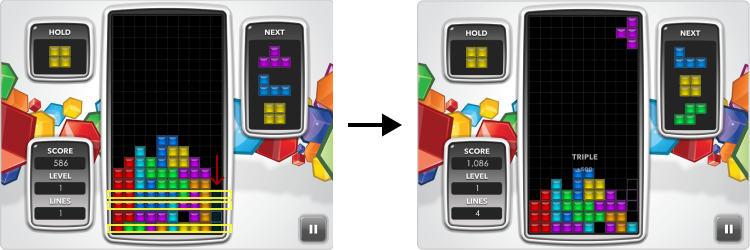
テトリスで高いスコアを出すためには、4 段一気に消すことや、コンボ（連続で段を消すこと）、T-Spin、さらには全消しなどが重要になり、奥が深いゲームです。

テトリスの AI にはいろいろなものがありますが、強い AI であれば、何手先も読み、次に落ちるピースの情報もすべて利用して、スコアの最大化を狙います。最強格の AI のひとつはビームサーチ（本記事では説明しませんが、よく使われます）というアルゴリズムを利用し、以下の動画のように、トッププレイヤーのレベルで戦うことができています。

Tetris God VS Best A.I. (by Wumbotize) - YouTube

1-3. 本記事で紹介すること

このように、できるだけ良い解を求めるタイプの問題を、アルゴリズムを長い時間かけて改良していくイメージをもって「マラソン型課題」⁵ ということにしましょう。（問題の性質から、ヒューリスティクス型課題とよばれることもあります）

1.2 節で紹介した 3 つの問題で見たように、一見コンピューターには解きにくそうに見える問題でも、とても良い答えを出すことができます。しかも時には、まったく規則性のない非人間的な解を作り出してきます。

このような非人間的な解を見て、驚かれた読者の方々もいると思います。また、こんなことをするのは大変ではないかと思っている方々も多いでしょう。確かに、最先端のアルゴリズムは、数々の工夫や改良をもとにした複雑なものになっています。

しかし、最先端とまではいかなくても、実は比較的単純なアルゴリズムでかなり良い答えを出せることも多いのです。本記事の 2 章以降では、このような問題に取り組む際の「最初のステップ」を教えたいと思います。

1-4. 競技プログラミングにおける「マラソン型コンテスト」

ここでは、競技プログラミングの（AtCoder Beginner Contest などで出題されるような）問題と、これらの「マラソン型課題」が、特徴としてどのような点が違うのかを説明します。（競技プログラミングをやっていない方は、読み飛ばしてもかまいません）

ABC などで出題される問題の特徴

AtCoder Beginner Contest (ABC) や情報オリンピックなどでは、「問題の答え（＝正解）を求めるプログラムを書く」ことが求められます。どんな入力が与えられても正しい答えを返す "正解" のアルゴリズムを考えることになります。そのため、

• 想定されるアルゴリズムが 1 つだけのこともよくあり、「正解」に至るための考察力が重要
• また、例えば ABC では 100 分で 8 問を解くといったように、素早い実装力が重要

といった特徴があります。

マラソン型課題の特徴

一方で、マラソン型課題は少し違い、ざっくりと言えば「できるだけ良いスコアを出せるプログラムを書く」ことが求められます。ゲームやパズルのスコアを競うような感じで、プログラムが得たスコアで順位が決まります。そのため、

• ABC などの問題にあるような「絶対的な正解」のようなものはない
• その代わりに、「どうやれば上手くいきそうか？」を直感を働かせて考えることが重要
• また、今のアルゴリズムの欠点を見つけ、これを改善するといったプロセスも重要

といった特徴があります。

"マラソン型" のコンテスト

競技プログラミングには、ABC のようなコンテストだけでなく、マラソン型課題を解くコンテストがあります。そのような「マラソン型コンテスト」を主に 3 つ紹介したいと思います。

AtCoder Heuristic Contest (AHC)

AtCoder Heuristic Contest (AHC) は、日本の競技プログラミングのサイト AtCoder が 2021 年 3 月から始めた新しいコンテストです。

• コンテスト期間が 5 時間程度の「短期コンテスト」と、コンテスト期間が 1～2 週間の「長期コンテスト」が、それぞれ 3 ヶ月に 1 回くらい開催される
• コンテストの参加者数が比較的多く、毎回 500 人くらい参加する
• 問題文が日本語でも提供される

といった特徴があります。

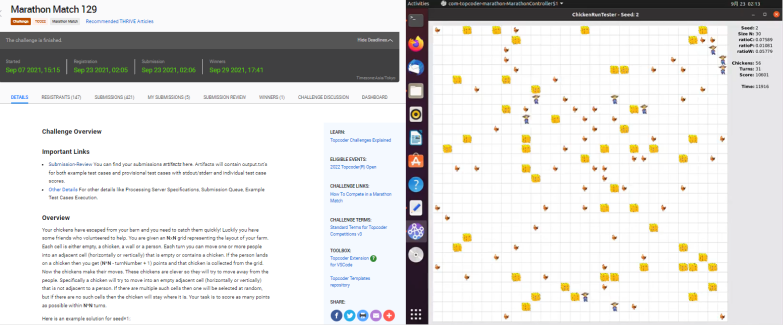
TopCoder Marathon Match (MM)

TopCoder Marathon Match (MM) は、2006 年から開催されている伝統的なマラソン型コンテストです。色々なプログラミングのコンテストを開いているアメリカ合衆国のサイト TopCoder が開催しています。

• コンテスト期間が 1 週間以上の「長期コンテスト」が多い
• パズルを解くような問題から実務に近い問題まで幅広く出題される
• コンテストでよい成績を残すと、アメリカで行われる TopCoder Open という大会に出場できる

といった特徴があります。

CodinGame

CodinGame では、他の 2 つとは異なり、ゲーム AI のコンテストが定期的に開催されています。ゲームをプレイするプログラムを書いて、他の参加者のプログラムと対戦させることで競います。

マラソン型課題とは少し違いますが、ゲーム AI でも問題に取り組む際の考え方が似ていたり、「ビームサーチ」などのマラソン型課題で定番のアルゴリズムがよく使われたりするので、これもおすすめです。

2. 問題の取り組み方

記事をここまで読んで、このような疑問を思い浮かべた方も多いと思います。

• Q1. マラソン型課題には、どうやって手を付ければいいのか？
• Q2. どのようにして効率的な解法を思いつくのか？
• Q3. 典型的なアルゴリズムはあるのか？

ここからは本記事のメインの内容に入りますが、1 つの問題を通して、マラソン型課題にどのように取り組むのかを説明します。

2-1. 問題

ところで、問題の取り組み方を説明するために、今から解いてほしいパズルがあります。

下の図を見てください。あなたは、10 個の丸の中に 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 をひとつずつ書き込みます。ここで「線でつながっている 2 つの数字の差の 2 乗」を合計した値をスコアとします。どこまでスコアを小さくできますか？

（スコアをできるだけ 最小化 することに注意してください）

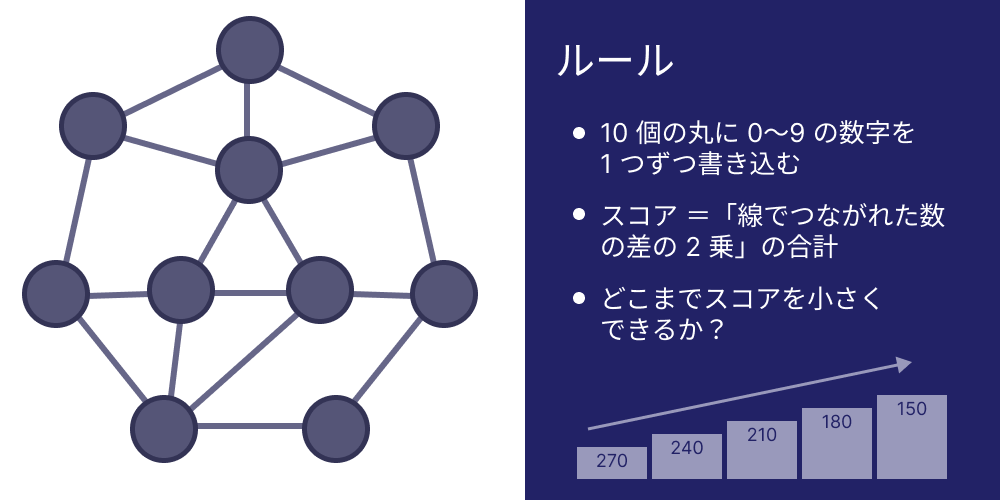
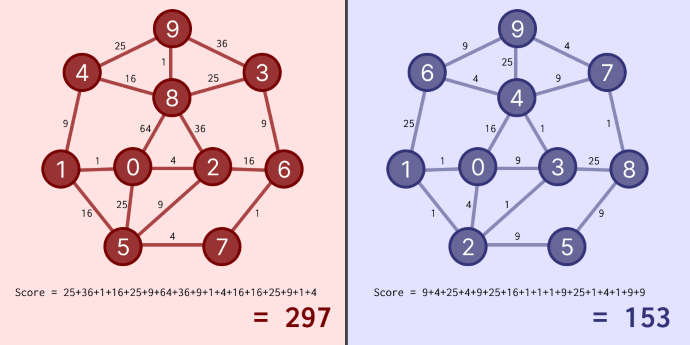
数字の書き込み方によって、スコアが大きく変わります。左図のような書き込み方をすれば 300 程度ですが、右図のような書き込み方をすれば 150 程度となり、より良いです。（下図で線の近くに小さく書かれた数は差の 2 乗を表しています）

この記事を読んでいるみなさんは、紙と鉛筆を取り出して、10 分くらいこの問題を手計算で考えてみてください。ここではコンピューターを使わないでください。講義の参加者の中にはスコア 103 を出した人もいます、ぜひこの記録に挑戦してみましょう。

（画像は https://unsplash.com/photos/IXYVzgwr2k0 より）

2-2. どうやって解いた？

みなさんに質問が 2 つあります。

• Q1. スコアいくつまで減らせましたか？
• Q2. どのような方法で取り組んだか、説明してみましょう。

もしランダムに数字を割り当てたとすれば、例えばスコア 150 以下を達成する可能性は約 300 回に 1 回しかありません。だから、きっと何か「工夫」を考えて、これを使ってこのパズルに取り組んだのでしょう。

おそらく、読者のみなさんの多くは、今から説明する 2 つのアプローチのどちらか、あるいは両方を組み合わせて解いたと思います。

方法 1 － 広げていく感じで答えを作る

スコアを小さくするためには、線でつながれた 2 つの数をできるだけ近くする必要があります。逆に、例えば「0」と「9」が線でつながっていたら、これだけでスコアが 81 も増えてしまうので、避ける必要があります。

そのため、以下の GIF 画像のような感じで、できるだけ隣り合うところに近い数字が来るように、0 から順に数字を書き込んでいった人も多いでしょう。

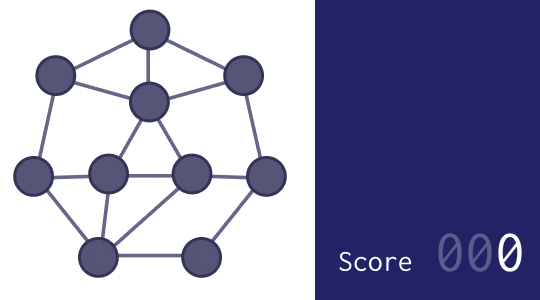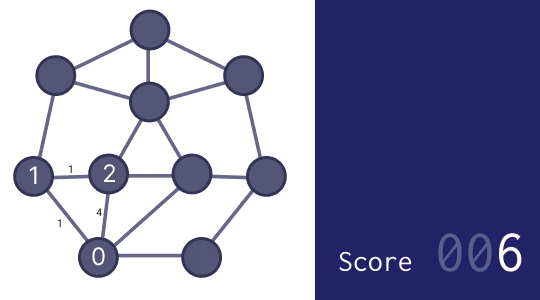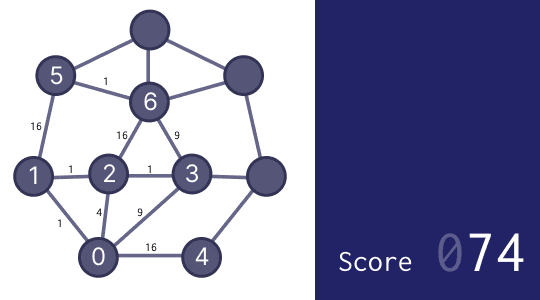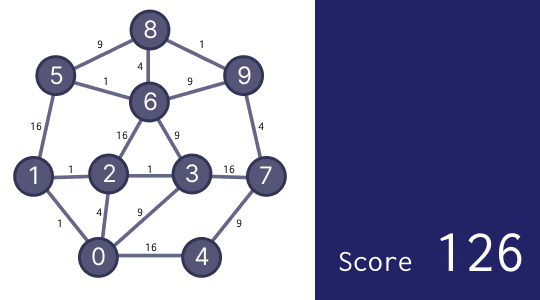
方法 2 － 小さな改善を繰り返す

パズルに取り組んでいるうちに「こことここを交換すれば、より良くなるのでは？」と考えた人もいるでしょう。

具体例として下図の場合で考えてみましょう。例えば「5」と「6」を交換すると、なんとなく改善できそうな気がします。ここで、実際にスコアを計算してみると、153 → 150 に改善できていることが分かります。

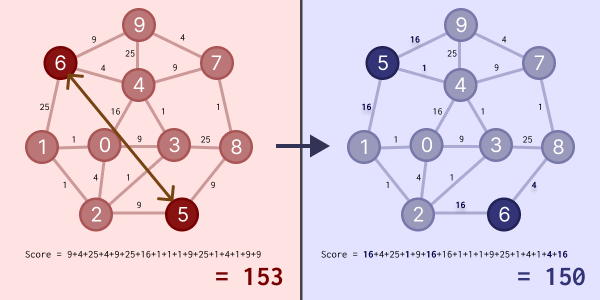
1 回の改善は小さいですが、この「小さな改善」を何度も繰り返すことで、どんどん答えを良くしていこう、というアプローチが考えられます。

2-3. コンピューターで解くような問題

このパズルは、丸の数が 10 個、線の数が 17 個（グラフ理論の言葉でいえば、10 頂点 17 辺のグラフ）という小規模なものでした。実際にコンピューターで解くような問題は、より規模が大きく、1000 個や 10000 個のデータを扱う必要があります。

しかし、コンピューターは人間よりも圧倒的に高速に計算できることを忘れないでください。一般のコンピューターは、1 秒で数億回の計算を行えるとされています⁶。そのため、先ほどのアイデアをコンピューター・プログラムに実装できれば、丸の数が 1000 個や 10000 個という大規模な場合でも、最適に近い答えを短時間で出すことができます。さらに、1.2 節で紹介したようないくつかの問題例でも、一見非人間的に思える解は、実はこのような「人間的な」アイデアをもとにして作られているのです。

このようなことをするためには、先ほどのようなアイデアを「アルゴリズム」の形にする必要があります。人間はふんわりした思考ができますが、プログラミングで解くためには「どうやって答えを出すか」のルールを厳密に決める必要があります。

続く 3 章・4 章では、先ほど述べた 2 つのアイデアを、どのようにして「アルゴリズム」の形にするのか、そして「貪欲法」「山登り法」の 2 種類の典型アルゴリズムを解説します。ここで扱ったパズルは実際のマラソン型課題の縮図だと思って読んでいただけるとうれしいです。

3. 貪欲法

まずは、1 つ目の「広げていく感じで答えを作る」方法について考えてみましょう。

この方法では、0 から順に「できるだけその数を置いたほうがよさそうな場所に」置いていくことになります。これは、「次ここに置くとどのくらい良さそうか」を評価する、いわゆる 1 手先読みの戦略になります。

これだけではピンと来ないかもしれないので、「1 手先読みの戦略」のイメージを 2 つ紹介したいと思います。

3-1. イメージ ①：球拾い

ところで、あなたは野球やテニスをやったことがありますか？その練習をしている時には、たくさんのボールを使うことになるので、後々ボールを回収する必要が出てきます。

練習を終え、地面にボールがたくさん（100 個くらい）落ちているとします。あなたはこのボールを全部元に戻さないといけません。でも、手間はかけたくありませんね。どうしますか？

おそらく多くの人は、まだ回収されてない近いボールに進んで、ボールを回収することを繰り返すでしょう。そうすれば、短い移動距離ですべて回収できるはずです。

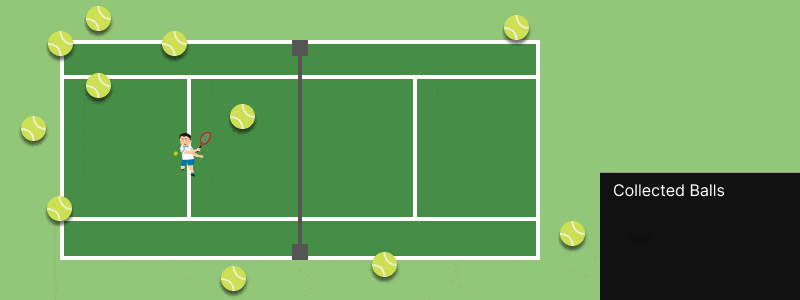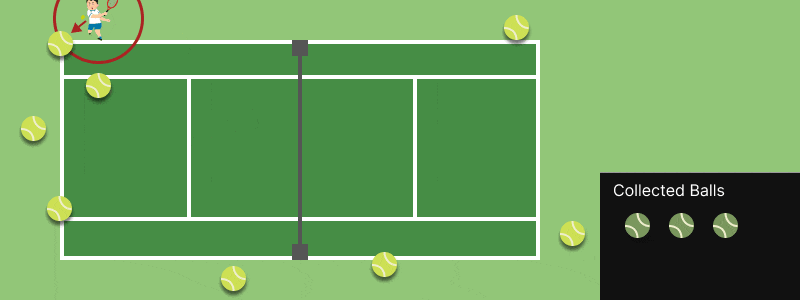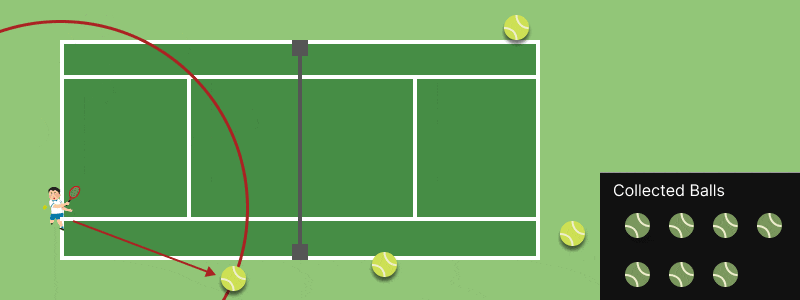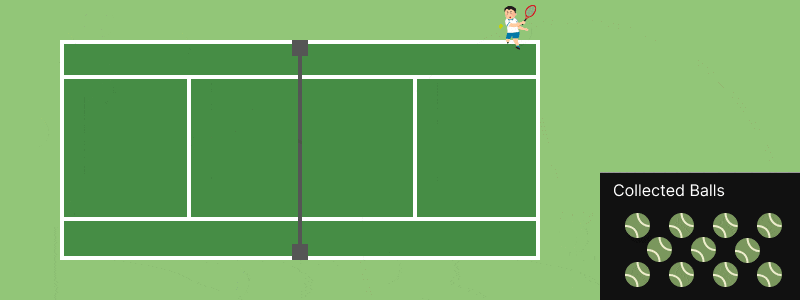
もちろん、この方法が最適解ではないこともあります。でも、効率は十分良いし、あまり考えずに動けるので、多くの人間は感覚的にこのような「アルゴリズム」を使って球拾いをしているのではと思います。

これは、ある意味では「2 手先以降のことを考えずに、とりあえず次のボールを最も早く回収することを狙う」1 手読みの戦略になっています。

3-2. イメージ ②：課題のスケジュール決め

みなさんも、学校の課題に追われる日々を過ごしたことがあるのではないでしょうか。学校の課題には締め切りが設定され、これに間に合わなければ減点されたり、ときには単位を落としたりするものです。だから、例えば 1 週間で 10 個もやるべき課題がある状況に追い込まれたら、課題を好きな順番でやるわけにはいかず、計画的にやる必要が出てきます。そんな時、どういう方法で次にやる課題を選びますか？

例えば（今日は 11 月 1 日として）、あなたが以下の 7 個の課題をやる必要があるとします。しかし、課題には時間がかかるので、1 日につき 1 個しかできません。

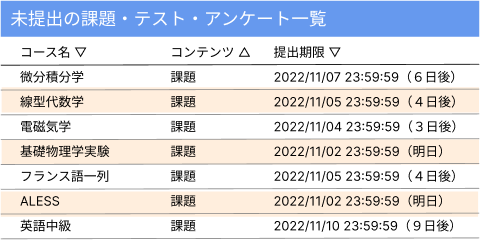
ここで、今日は好きな科目「線型代数学」の課題をやろう、と思ったとします。しかし、そうすると次の日、「基礎物理学実験」「ALESS」の課題の期限が当日になり、すべての課題の提出期限に間に合うのが不可能になってしまいます！

そのため、今日はどうしても「基礎物理学実験」か「ALESS⁷」のいずれか一方の課題をやらなければなりません。

一般的に、やらなければならないタスクが何個もあるときは、締め切りの早い順にやるとリスクがより抑えられることが知られています。実際に上の例で確かめてみましょう。確かに、締め切りが一番早い課題を選び続けると、すべての課題が提出に間に合うことが分かるでしょう。

この方法は「次に一番選ぶべき感じの課題を選ぶ」という 1 手読みの戦略になっています。このように、現実のいろいろな場面でこの手法を無意識に使っていることが分かります。

3-3. パズルを解いてみよう

では、方法のイメージがつかめたところで、実際に先ほどのパズルで良い答えを出せるアルゴリズムを設計してみましょう。

2.2 節で紹介した方法 1 では、0 から順に数を書き込んでいきますが、そのためには「次に数を書き込む場所をどういう基準で決めるか」を厳密に決める必要があります。つまり、例えば下図のような状態のときに

• 次は A～E のどこに 5（次の数）を書き込むべきか？
• この判断は、どのようなルールで行うか？

といったものを考える必要があります。

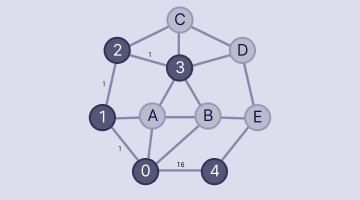
人間は感覚で数を書き込んでいけるかもしれませんが、コンピューターには感覚といったふんわりしたものはなく、厳密なルールに従ってしか動けないからです。なので、ここでは「人間の思っている感覚をどう "ルール化" するか」が重要になってきます。

それでは、始めましょう。

アルゴリズム ①

線でつながれた 2 つの数が近くなれば、スコアが小さくなりそうです。なので、まずは次のような基準で数を書き込むことにしましょう。

基準　隣り合う数が「次に書き込む数」に近い場所ほど、書き込んだほうがよい。

つまり、上の図の例では E に書き込むのが（4 と隣り合うので）最も良いだろう、ということになります。これは、果たして上手くいくのでしょうか。実際にやってみましょう。

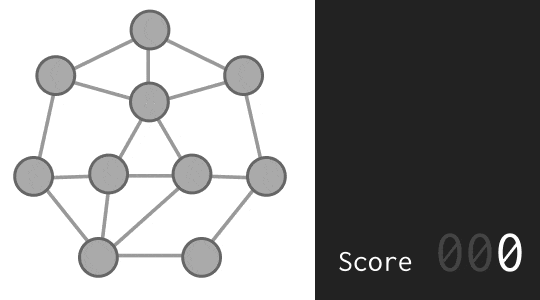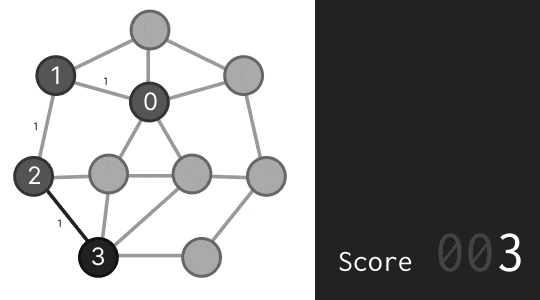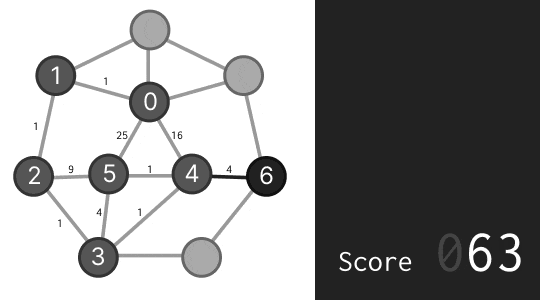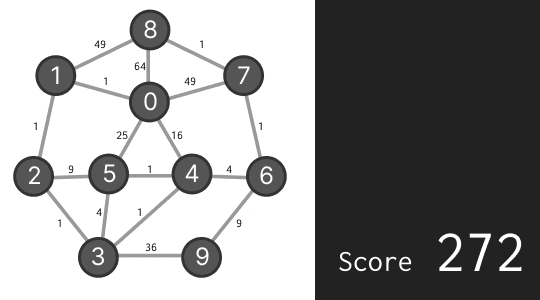
スコア 272 と、全然ダメな結果が返ってきました。このようになった理由は「0 と 8」や「3 と 9」のような離れている数が線でつながっているからです。スコアは差の 2 乗の合計なので、差が 8 や 9 のものが 1 カ所でもあれば、これだけで悪い答えになってしまいます。

アルゴリズム ②

アルゴリズム①の結果を見ると、やはり「差が大きい場所」を作らないのが大事な気がします。つまり、このような場所があれば早めに "封鎖" するイメージです。なので、アルゴリズムを変えて、次のような基準で数を書き込むことにしましょう。

基準　隣り合う数が小さい場所ほど、書き込んだほうがよい。

つまり、先ほどは（3.3 節の最初の図の例では）E に書き込むのが最も良いとしていましたが、0 を早く "封鎖" するために A か B に書き込むのが最も良いだろう、ということにします。では、実際にやってみましょう。

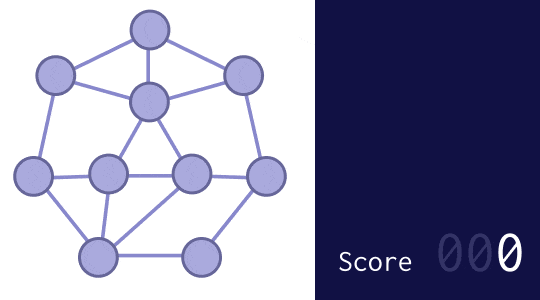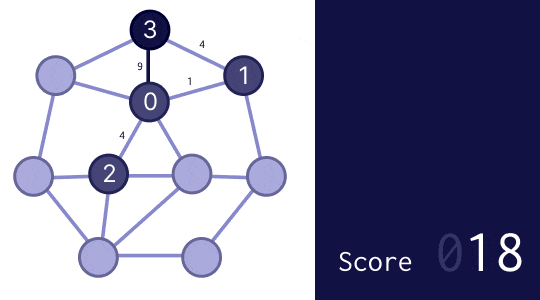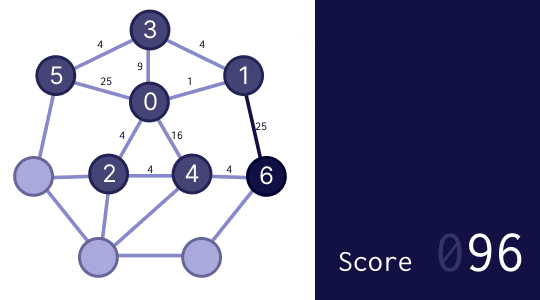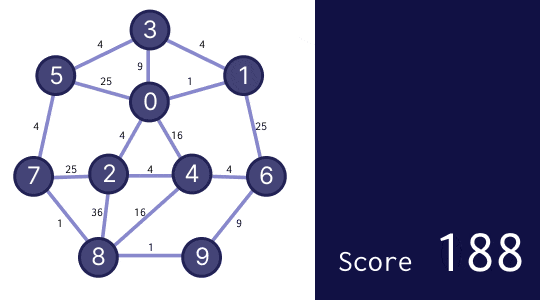
スコア 188 と、まあまあ良くなりました。ここからさらに改良するにしても、この基準を基本方針とするのがよさそうです。

アルゴリズム ③

アルゴリズム②では、隣り合う数が最も小さい場所が複数あるときに、このうちどれを選んでもよいとやっていました。3.3 節の最初の図の例では、A と B どちらに書き込んでも同じと判断していました。しかし、A を選んだほうが「1」も同時に "封鎖" できて良いのではと考えられます。

なので、これを改良して、次のようにしたらどうなるでしょう？

基準　隣り合う数の中で一番小さいものが小さい場所ほど、書き込んだほうがよい。これが同じ場合は、隣り合う数の中で 2 番目に小さいものが小さい場所ほど、書き込んだほうがよい（3 番目以降も同様）。

結果は次のようになります。

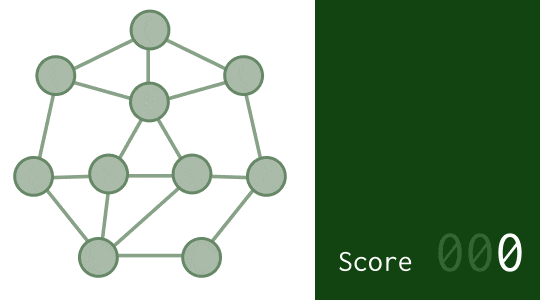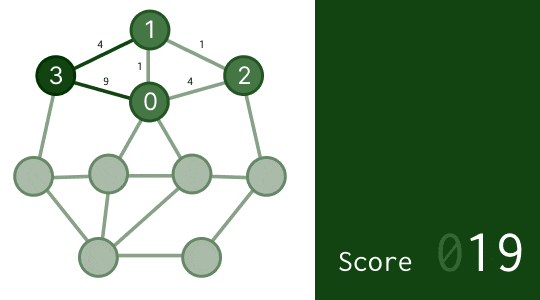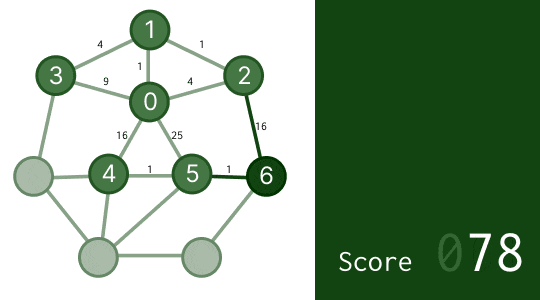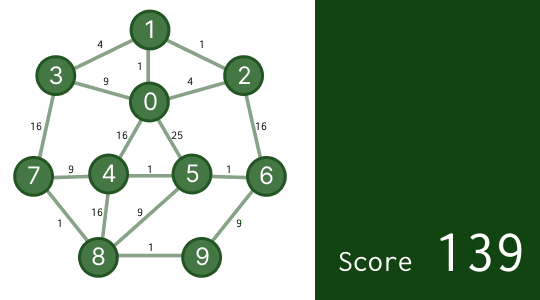
スコア 139 と、かなり良い答えを出せるようになりました。これでもう最適解の 1.4 倍くらいまできています。データの数が今より大きくなっても、高速にある程度良い解を出せそうなのが分かるでしょう。

アルゴリズム ④

最後に、また別の改良を考えてみましょう。

アルゴリズム③の例では、最初に「0」を書いた場所から 5 本の線が出ているので、必然的にここだけで 1² + 2² + 3² + 4² + 5² = 55 のスコアが増えてしまいました。これを考えると、0 は出ている線の数が少ない場所に書くほうがよさそうです。次の基準で書き込む場所を決めてみましょう。

基準　基本的にはアルゴリズム③の基準を採用する。ただし、その基準で同率になった場合、隣り合う「まだ書き込まれていない」丸の個数が少ないほど（つまり、出ている線の数が少ないほど）書き込んだほうがよい。

実際にやってみると、次のようになります。

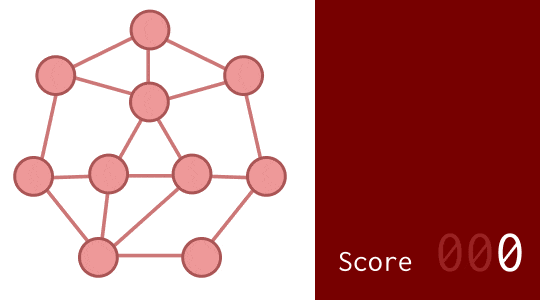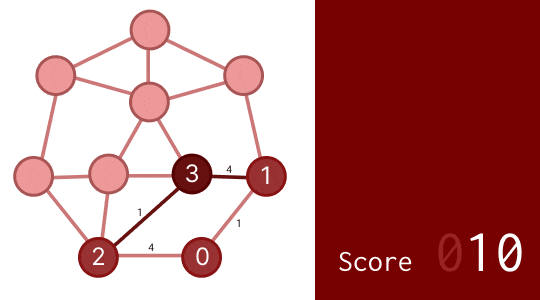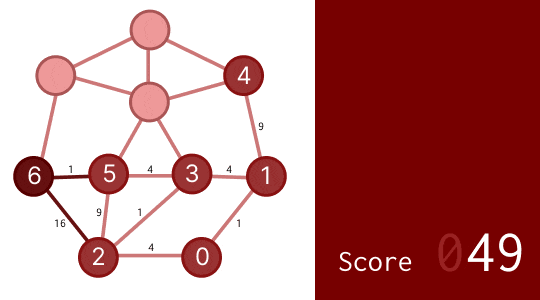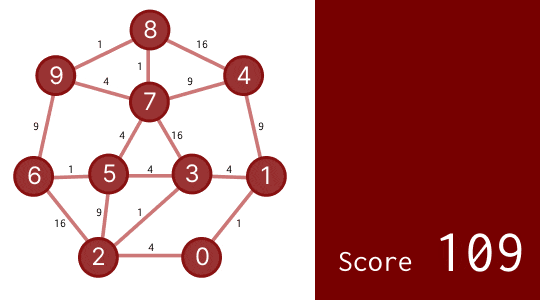
スコア 109 になりました！実はこれで最適解の 1.1 倍を切っており、とても良い答えを出せています。

3-4. 貪欲法とは？

このように、「今の状態からできる最も良さそうな行動」を選び続けることで良い感じの答えを出す、1 手読みの戦略を使った方法を 貪欲法 (Greedy Algorithm) といいます。（貪欲法のイメージが分からない場合は、3.1 節・3.2 節を振り返ってください）

先ほどのアルゴリズム①～④はすべて貪欲法のアルゴリズムですが、選ぶ "基準" を改良すれば、（不思議なことに？）とても良い解を出すことができました。この例のように、貪欲法はマラソン型課題を解くときに有効な手法の 1 つであり、工夫次第では（1.2 節で述べたような）非常に質の高い答えを出せる場合もあります。

また、今回の例のように、計算量の面でも高速に動作する⁸ことが多いので、データが大きい場合には特に有効活用できます。

3-5. いろいろな「貪欲法」

読者のなかでアルゴリズムをよく知っている方は、貪欲法を コイン問題（1.1 節参照）や 区間スケジューリング問題 などを解くアルゴリズムとして認識しているかもしれません。

これらの問題は、どんな入力ケースに対しても貪欲法で最適解を出すことができます。このような貪欲法で "解ける" 問題もあるということを知っておいてください。3.2 節で説明した課題のスケジュール決めの例もそうで、締め切りの早い順にやる貪欲法を使うと、どんな状況でも提出できる課題の数を最大にできます。

当然、直感にしたがって考えた貪欲法では、最適解が求められないような問題も多いです⁹。しかし、このような問題でも、貪欲法の基準の工夫次第では、とても良い答えを出せる場合だってあります。貪欲法は、マラソン型課題に対してもよく使える手法です。

4. 山登り法

次に、2 つ目の「小さな改善を繰り返す」方法について考えてみましょう。

この方法は「この 2 つの数を交換したら、スコアは良くなるかな？」と試して、良かったら採用する、というものです。一回の改善は小さくても、これを繰り返せば自然と最適に近い答えに到達するはずだ、というアイデアです。

これを自力で思いついた読者もある程度いるでしょうが、思いつかなかった方にとってはあまり直感的ではないと思います。なので、今からこの「小さな改善を繰り返す」戦略のイメージを 2 つ紹介します。

4-1. イメージ ①：敷き詰めパズル

みなさんは、ジグソーパズルのようなパズルを解いた経験はありますか？このとき、どんな方法を使って解きましたか？説明のため、似たような簡単な例として、5×5 のマス目に 5 つのピースを全てはめるパズルを考えてみましょう。

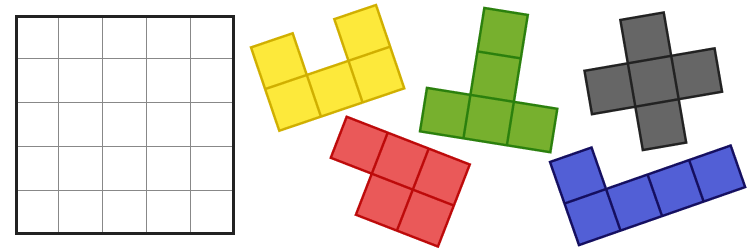
4 ピースは簡単にはまるけど、残りの 1 ピースがはまらない… これが、こういうパズルの難しいところです。一気に 5 つ全部はまるのは、むしろレアケースだと思います。（下図は 4 ピースしかはまらない例）

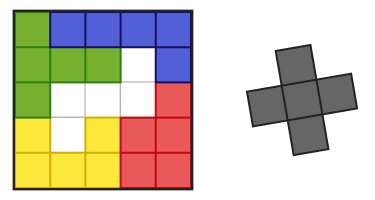
こんな時、どうやって解決しますか？例えば…

ピースの配置をほんの少し変えてみて、灰色のピースがはまるようになるかな？

というふうに試行錯誤するでしょう。

では実際に、黄色いピースと赤いピースの位置を交換してみましょう。すると…

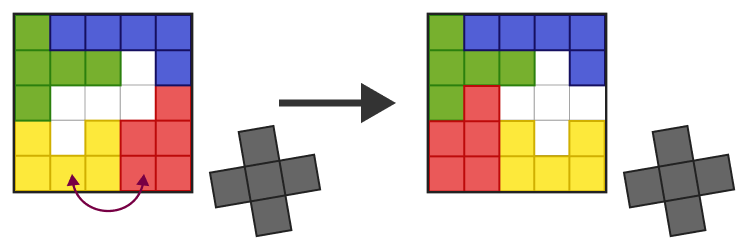
灰色のピースがはまる形になり、パズルが解けました！このように「小さな改善を繰り返す」ことで、はまるピースの数をどんどん増やしていき、最終的に人間はパズルを完成させることができるのです。

4-2. イメージ ②：文章校正

私たちはよく（日本語か外国語かにかかわらず）文章を校正します。なぜなら、基本的に誰でも、いきなり書いた文章にはミスがあったり、文法的に間違っていたり、あるいは伝わりにくかったりするからです。

では、どうやって文章を校正するのでしょうか。おそらく、

• 文章をながめて「ここはこう修正すべきだよね」「ここをちょっと修正したら良くなるかな？」という場所を見つける
• ここを修正してみて、実際によくなったら修正を採用する

というプロセスを繰り返して、文章をどんどん良くしていくのではないかと思います。修正すべきか迷うこともありますが、この時はそれぞれの文章をよく評価して、どちらが良いか考えることになるでしょう。

具体例として、誰かが "He is student in Tokyo University." という英文を書いたとしましょう。この文章にはいくつかミスがあり、いずれ校正されなければなりません。校正のために文章を見てみると、例えば次のようなことが思い浮かびます：

「is と student の間に "a" を入れてみると、良くなるんじゃないか？」

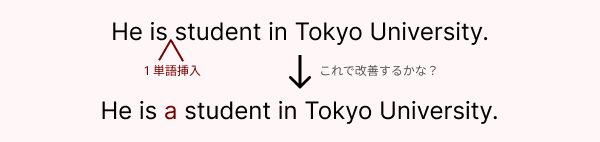
すると、元の文章が 40 点くらいだったのが、70 点くらいに改善した¹⁰ので、この修正を採用する。そんな感じで校正が進んでいきます。このプロセスを繰り返せば、気づいたら完璧に近い文章ができあがっています。

このように「小さな改善を繰り返す」ことで、全体としても文章のミスがどんどん減ったり、分かりやすくなったりする、これが校正作業です。

私たちは日常的に、質の良いものを作るときに「小さな改善を繰り返して答えを良くしていく」アイデアを無意識のうちに使っているのです。

4-3. パズルを解いてみよう

では、方法がつかめたところで、実際に先ほどのパズルで良い答えを出せるアルゴリズムを設計してみましょう。

2.2 節で紹介した方法 2 は、「2 つの数を交換する」という全体からみれば小さな改善を繰り返すことで、答えをどんどん良くしていくというアイデアでした。これをプログラミングで実装するのは、もしかすると貪欲法よりも単純かもしれません。

アルゴリズム

人間は「どの 2 つの数字を交換したらよさそうか」を無意識的に選び出すでしょうが、いきなりコンピューターにこれをやらせるのは難しいです。でも、2 つの数をランダムに選んだとしても、それなりの性能が出せます。

アルゴリズムとして書いてみると、次のようになります。

1. はじめに、初期解¹¹として 0～9 の数字をランダムに書き込む
2. 次の操作を一定回数繰り返す
   a. ランダムに 2 つの数字を選ぶ
   b. 選んだ 2 つの数字を交換して、スコアが減少する（＝解が良くなる）ならば、その交換を採用する
3. 最終的に、かなり良い解が得られることが期待できる

文章だと分からないかもしれないので、図でも説明してみました。

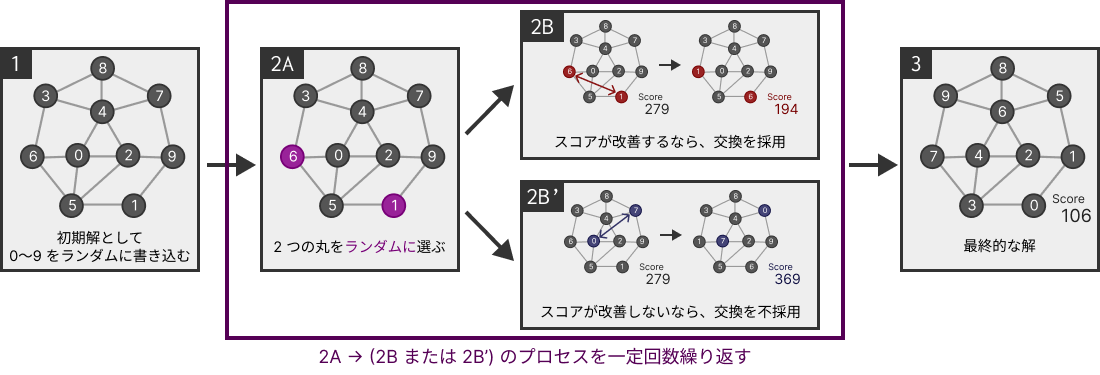
実行結果

このアルゴリズムは、どのくらい性能が良いのでしょうか？

実際にパズルを解いてみると、以下の図のように答えがだんだんと改善していき、最終的にスコア 106 を達成することができました。

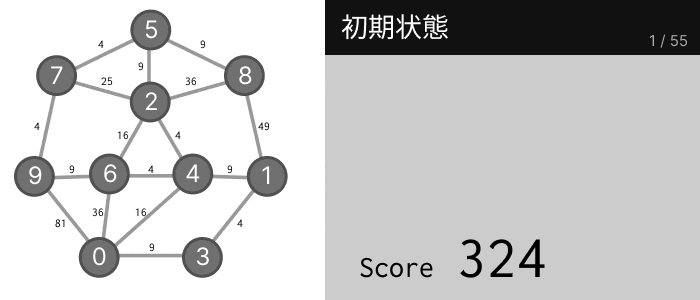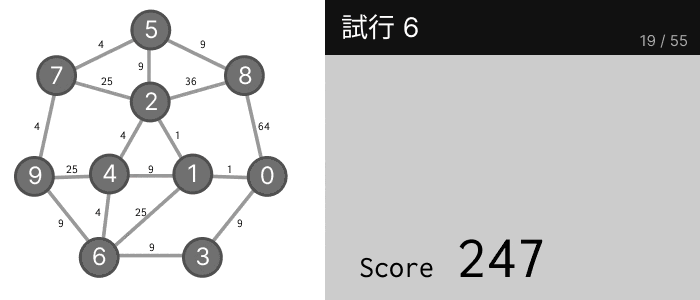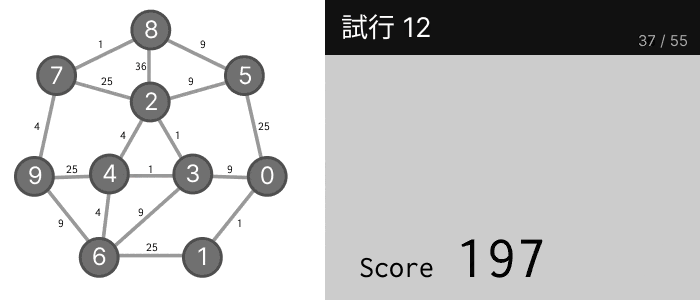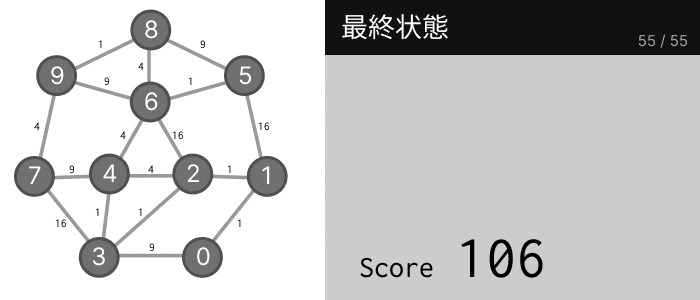
すべてはランダムで動いているので、最終的にどの答えにたどり着くかは確率的です。これは当然、最適解ではないのに、次にどのように 2 つの数を交換しても、スコアが増加してしまうこがもあるからです。でも、106 という良いスコアが得られたのは全く偶然ではありません。実は、これ以上改善できなくなるまで繰り返せば、33% の確率で最適解（スコア 100）が得られます。

十分良い答えを得るためには、試行を 50～100 回くらい繰り返す必要があります。確かに、人間にとっては多いかもしれません。でも、コンピューターにとっては、データが 100 個や 1000 個のときでも、この方法で最適に近い答えをすぐに求めることができます¹²。

4-4. 山登り法とは？

このように、「小さな変更を試す → スコアが良くなればこれを採用する」を繰り返すことで答えをどんどん良くしていくアルゴリズムを、山を登る場面にたとえて 山登り法 (Hill Climbing Algorithm) といいます。（山登り法のイメージが分からない場合は、4.1 節・4.2 節を振り返ってください）

4.3 節では山登り法を使ってパズルの良い答えを求めました。ここでは「小さな変化」として 2 つの数の交換だけを使いましたが、もっといろいろな種類の「小さな変化」がよく使えるときもあります。例えば、文章校正の例（4.2 節）においては、1 単語挿入・1 単語削除・1 単語変更・2 単語の場所の入れ替え・2 文の場所の入れ替えなど、いろいろ使えます。マラソン型課題に取り組むときは、直感的に良さそうなものを考えてみましょう。

4-5. いろいろな「山登り法」

山登り法では、どのように「小さな変更」を行ってもスコアが改善しない 局所的最適解 に落ちることがあります。例えば、先ほどのパズルのスコア 127 の解（下図）は、最適解ではないのに、どの 2 つの数を交換してもスコアが改善しません。

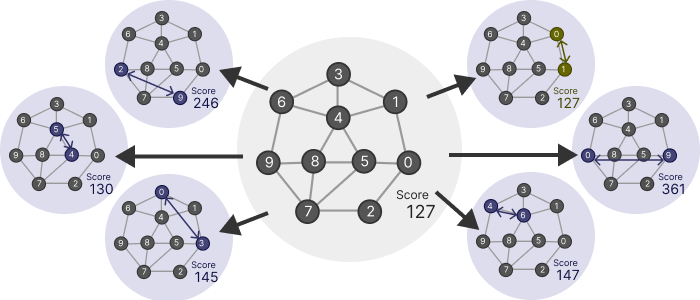
当然、局所的最適解に落ちると、何回試行しても山登り法がこれ以上進みません。このような状況を防ぐために、いくつかの工夫が思いつきます。そのうち代表的な 2 つを紹介します。

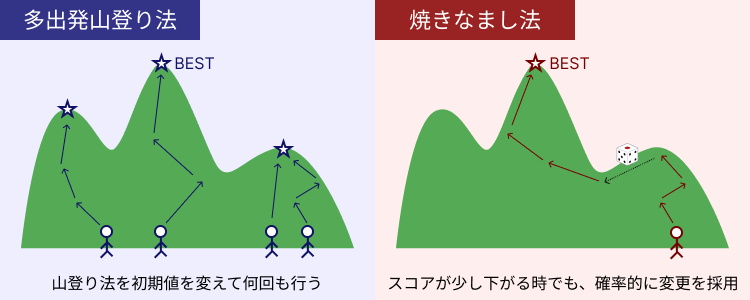
工夫①：多出発山登り法

山登り法で最終的にどの答えにたどり着くかは確率的で、その局所的最適解のスコアが大きく振れることがあります。このような場合は、時間が許す限り、山登り法を初期値を変えて何回も行うという工夫が考えられます。これを多出発山登り法といいます。

工夫②：焼きなまし法

山登り法の局所的最適解から脱出するために、「スコアが少し悪くなるときでも、確率的に変更を採用する」という工夫ができます。これを焼きなまし法といいます。

変更を採用する確率は、スコアが少ししか悪化しないときは高く、スコアが大きく悪化するほどゼロに近くなるようにします。（一般的には、定数 $\alpha \lt 1$ をうまく設定して、変更を採用する確率を $\alpha^{スコアの減少幅}$ にすることが多いです）

多出発山登り法と焼きなまし法は、それぞれ以下の図のようなイメージです。このように、山登り法の欠点を補って改良するアイデアはいくつもあります。

5. 本記事のまとめ

13000 文字の長い記事を読んでいただき、本当にありがとうございます。マラソン型課題の世界はいかがだったでしょうか？

本記事ではマラソン型課題を解く典型的なアルゴリズムとして「貪欲法」「山登り法」を解説しましたが、まだ扱っていないアルゴリズムもたくさんあります。例えば、ビームサーチ、遺伝的アルゴリズム、モンテカルロ法などが挙げられます。気になった方はぜひ調べてみてください。

でも、私がこの記事で最も伝えたいことは、実際に典型的な手法をあてはめることを超えて、どうやってマラソン型課題に取り組むかです。これらのアイデアの根底は「手でならどうやって解く？」の疑問があります。その疑問を 2 章でみたように自分の直感で考えること、そしてそれをプログラムに実装できるようにすること。これが問題に取り組む「はじめの一歩」だと私は思っています。

こうして、マラソン型課題に自力で取り組めるようになればいいなと思います。私が 4 年前にマラソン型コンテストに初めて出たときは、これを全然分かっていませんでした。この記事を 4 年前の自分に伝えたい。

1. 筆者はまだ大学 2 年生なので、実務経験はまだありませんが、最短経路問題やマッチング問題などのアルゴリズムが実務でもよく使われるという話を聞いたことがあります。 ↩

2. ここでは日本で使われる 1, 5, 10, 50, 100, 500 円硬貨の場合を考えています。 ↩

3. この文は「実生活に学ぶアルゴリズム【第 1 回：セブンイレブンでは 500 円で何カロリー得られるか？】」（@e869120 さん作）から引用しています。 ↩

4. 現在知られている最も良い解が最適解の可能性もないわけではありませんが、少なくともこれはまだ証明されていません。 ↩

5. 「マラソン型課題」という名前は、TopCoder Marathon Match に由来しています。AtCoder ではヒューリスティクスコンテストという名前を採用していますが、このような問題を解く際に近似保障のあるアルゴリズムが使われることもあるため、本記事では「マラソン型課題」という名前を採用しています。 ↩

6. 「問題解決力を鍛える！アルゴリズムとデータ構造」（大槻兼資 著）p.22 より ↩

7. ALESS は Active Learning of English for Science Students の略で、筆者が通っている大学オリジナルの授業です。英語で研究テーマを調べて実際に論文を書くというハイレベルな内容であるため、課題も大変であることで知られています。 ↩

8. 丸の数を N、線の数を M としたときに、アルゴリズム①～④はすべて計算量 O(NM) で動作します。また、データ構造を使ってさらに高速化することも可能です。 ↩

9. 競技プログラミングには「直感に頼った未証明の Greedy（貪欲法）は危険です」という格言があります。しかし、直感的な貪欲法で最適解にはならないケースはあっても、平均的にとても良い（最適に近い）答えを出せることも多く、マラソン型課題には有用です。 ↩

10. もちろん人によって採点基準は異なります。ここでは、評価値を利用するたとえとして、このような説明をしています。 ↩

11. 初期解は、このような「小さな改善を繰り返す」タイプのアルゴリズムにおいて、改善を始める前の一番はじめの解のことです。このパズルの例では、貪欲法で生成した解を初期解にするなどの工夫もできます。 ↩

12. 丸の数を N とすると、試行回数が N² のオーダーで増えることを予想しています。 ↩